分子筛吸附塔温度交变载荷下的热-力耦合应力场分析

2022-01-05陈建国王传平周兆明

压力容器 2021年11期

陈建国，王传平，熊涛，朱琳，周兆明，张佳

(1.新疆油田公司采气一厂,新疆克拉玛依 834000;2.西南石油大学机电工程学院,成都 610500;3.油气藏地质及开发工程国家重点实验室,成都 610500)

0 引言

压力容器的疲劳破坏已成为石油化工领域最常见的失效形式。据国外压力容器失效事故数据统计，压力容器疲劳失效约占30%[1-3]。其失效的根本原因：在交变载荷下，受压部件产生较大的局部应力集中(峰值应力)，一般达薄膜应力的3～6倍，最终导致压力容器疲劳断裂失效[4]。某分子筛脱水吸附塔工作流程为吸附→再生→吸附交替循环的过程，温度交变工况复杂，热吹最高温度290 ℃，时间5.5 h；冷吹温度30～40 ℃，时间6 h。在温度交变载荷下，吸附塔局部应力集中导致塔体失效，因此有必要对其交变载荷下热应力分布规律进行分析。

对于温度应力工作载荷下的压力容器疲劳失效已有较多研究。HASHIMOTO等[5]利用ABAQUS有限元软件对3种反应器封头进行了稳态热应力分析，结果表明，峰值拉应力主要分布在喷嘴的焊接区附近。CHAUDHRY等[6]利用数值模型对反应堆压力容器稳态(反应堆启动、关闭等)下的热应力进行了完整评估，结果表明，壁面应力最大的位置处于覆壳和容器交界面。FERREO等[7]对反应堆压力容器热应力过程进行了数值模拟，得到了热冲击作用下加载速率对应的动态参考温度T0,dyn，并与准静态参考温度T0,sta进行了比较。KANDIL[8]分析了稳态压力和温度共同作用下圆柱形压力容器的应力分布，得到了不同工况下平均应力与应力幅值之间的关系。刘磊等[9]考虑吸附塔的结构及管口载荷等因素，利用ANSYS软件对吸附塔模型进行结构应力与疲劳分析。王嫣然等[10]采用有限元法计算出薄膜型LNG 船各稳态温度下的结构温度应力，结果表明，底边舱折角处温度应力与船体外板水线面上下的温度差异呈良好的线性关系。

虽然有些学者分析了特定结构的热-力耦合作用，但对温度交变载荷下吸附塔的耦合效应研究较少。本文基于吸附塔瞬态热力学研究机理，系统分析分子筛吸附塔在温度交变载荷下的热-力耦合场，以揭示吸附塔瞬时热应力分布规律，为吸附塔压力容器结构设计及强度分析提供理论参考和技术支持。

1 基础理论

根据拉梅方程(Lame equation)，假设轴向长度无穷大，在内部压力Pw作用下，圆筒三向主应力计算如下：

(1)

式中,σr为径向结构应力；σθ为环向结构应力；σφ为轴向结构应力；K为外径和内径的比值；R0为圆筒外半径；r为任意半径。

在温度分布函数T(r)作用下，温度应力如下：

(2)

式中,σtr为径向热应力;E为弹性模量;μ为泊松比;α为线膨胀系数;Ri为圆筒内半径;σtθ为环向热应力;σtφ为轴向热应力。

根据热应力原理，热应力计算如下：

(3)

式中,σzr为径向耦合应力;σzθ为环向耦合应力;σzφ为轴向耦合应力。

根据von Mises的第四强度理论，等效热应力σe计算式为：

(4)

根据实际受力和温度载荷的情况，联合式(1)～(4)即可求出热应力[11-13]。

2 设计参数及数值模型分析

2.1 设计参数

某分子筛脱水吸附塔介质为湿天然气(不含酸气)，其主要性能参数见表1。塔体主体材料Q345R，管口锻件材料16Mn，裙座材料Q345R，根据GB/T 150—2011《压力容器》，Q345R材料物理性能如图1所示。

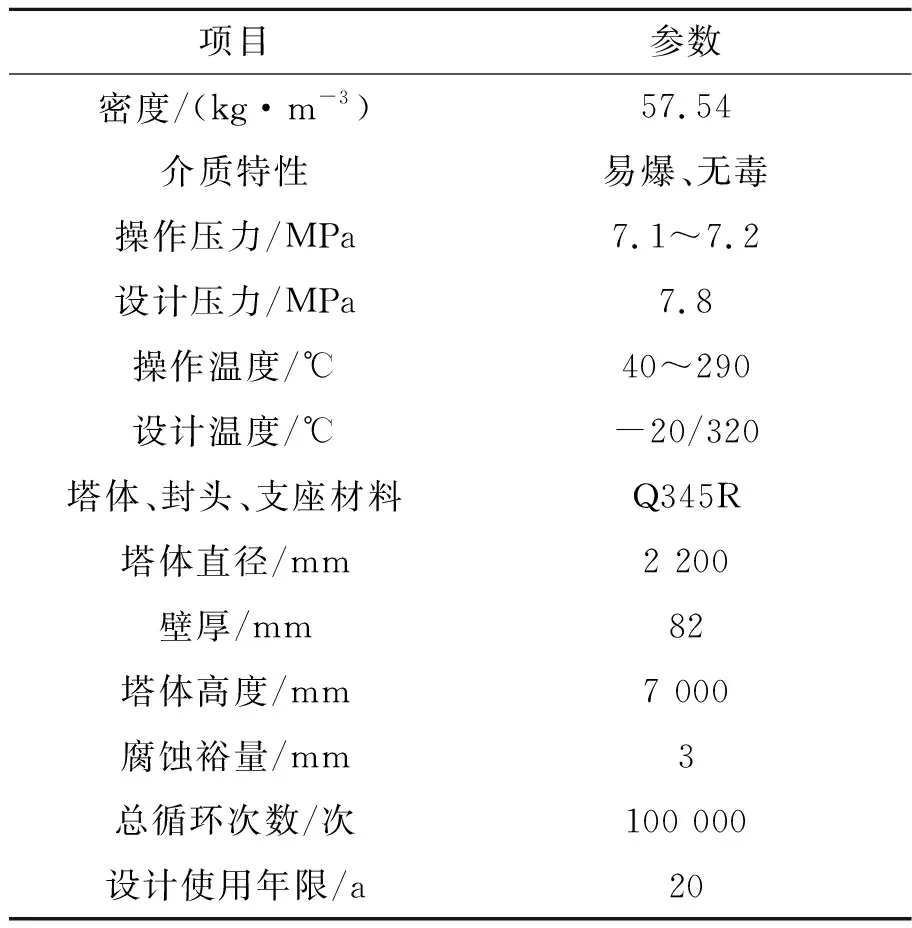
表1 吸附塔主要设计参数

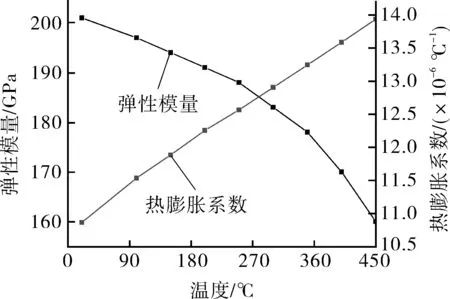
(a)弹性模量和热膨胀系数

2.2 数值模型

根据吸附塔结构特点和载荷工况，建立全尺寸吸附塔数值模型，对温度交变载荷下塔体安全风险进行分析评估。为减少计算量,YZ平面为对称截面，采用1/2对称模型，计算模型如图2(a)所示。边界条件采用与现场真实工况一致，温度和压力均采用现场操作条件，操作温度范围40～290 ℃，操作压力7.2 MPa；吸附塔内部处于压力和温度作用下，塔体外表面因保温材料的存在，设为绝热边界条件，热流密度接近于零；对壳体和接管置于不同的膨胀系数；弹性模量、热传导率及热膨胀系数等参数均采取随时间变化量。模型底部固定约束以限制刚体位移，上部使其处于自由状态，对称面为对称约束，接管端部施加轴向平衡载荷。为解决热-力耦合问题，热应力分析采用瞬态模块。由于封头、裙座、接管处为重点研究对象，因此取图2(b)路径A～H，分析每条路径上的热应力分布规律。

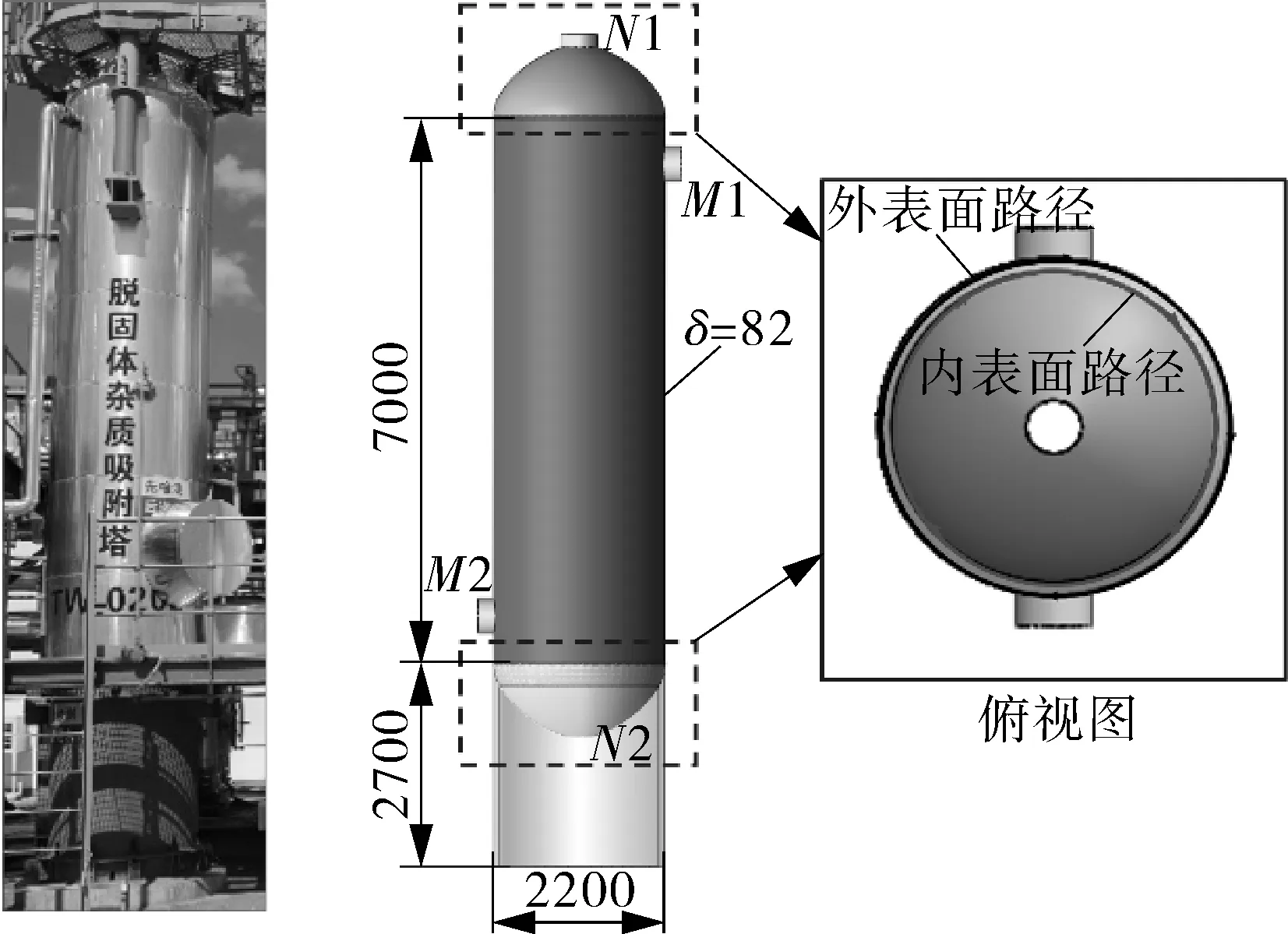
(a)数值计算模型

为提高计算效率，在模型过渡、转角与连接缝隙等位置增加网格数量，对过渡区域的网格进行了粗糙化处理。优化网格敏感性影响，得到最佳网格质量。

3 热力耦合分析

在应力和交变温度条件下，塔体会发生损伤累积。为了定量判断吸附塔管壁是否发生损伤，本文仅研究等效热应力高于屈服强度时的损伤累积。因此，将疲劳失效准则简化为用应力集中来判断是否发生损伤[14-16]。通过顺序耦合法分析吸附塔热应力分布规律，对吸附塔升温过程瞬时温度场进行运算，以运算结果为载荷，将其施加于结构模块进行塔体热应力分析。

图3为塔体热流密度分布。因接管N1，N2处气流方向与塔体重力方向一致，热流密度变化比较均匀，应力分布也比较均匀；接管M1，M2处热流变化剧烈，应力分布不均匀，产生的热应力更大(接管N1，N2，M1，M2如图2(a)所示)。

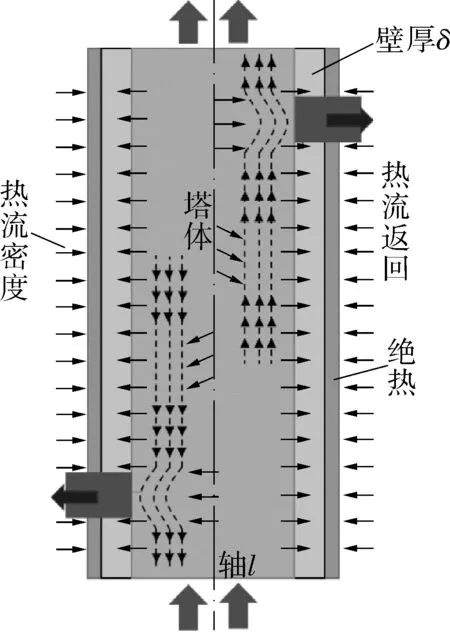
(a)热流密度简化示意

图4为吸附塔温度场分布。从图4(a)中可以看出，由于温度场水平不断升高，塔体内外壁呈现不同程度的温度变化。取接管M1，M2位置路径(路径a-a′和b-b′)上的温度场进行分析，见图4(b)(c)，可以看出沿着路径方向温度逐渐减小，即温度场沿塔体壁厚方向依次减小。

图4 吸附塔温度场分布

温度交变下的塔体热应力分布如图5所示。由于塔体内部热冲击作用，温差的叠加效应使塔体处于一个较高的应力场中。在交变温度作用下，吸附塔等效应力大多集中在 0～104.84 MPa之间。应力集中均出现在接管和壳体连接处，其原因是由于热应力作用下，塔内存在薄膜应力，塔体开孔导致承载截面减小，而使该截面的平均应力增加，由于变形协调，在接管和壳体相贯处产生一对剪力和弯矩，从而在壳体开孔边缘和接管端部产生局部弯曲应力，局部应力集中使物体产生疲劳裂纹。

图5 吸附塔热应力分布

由以上分析，由于M1，M2接管内壁位置存在较大的应力集中，因此取M1，M2接管位置的截面A,B,C,D(1/2截面)进行结果分析，得到表2所示截面应力分布规律。

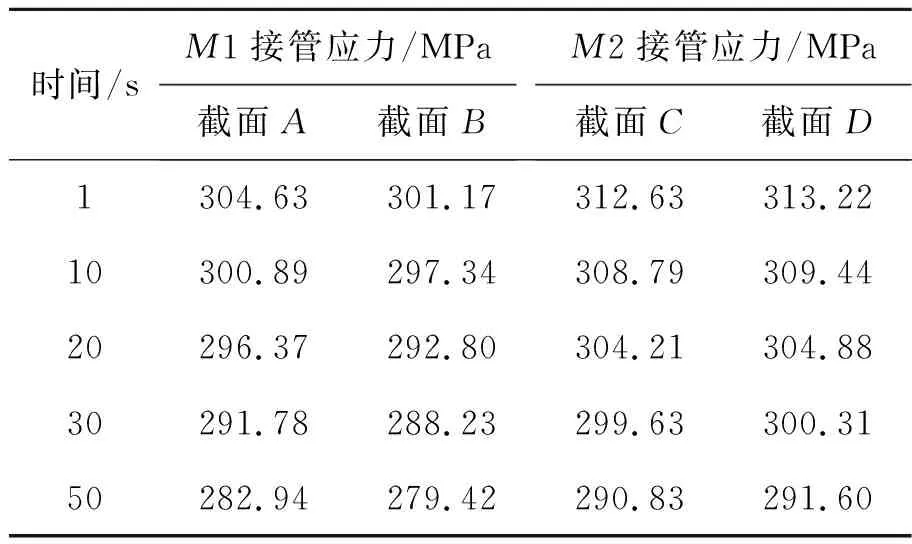
表2 M1，M2接管位置截面等效应力分布规律

由表2可以看出，在温度交变载荷作用下，截面C,D处应力大于截面A,B处应力，截面C,D的应力集中系数分别为2.54和2.55。随着时间的增加，最大等效应力逐渐减小，这是因为随着时间的增加，吸附塔塔体内部温度逐渐升高，塔体外表面短时间内热量与外界对流较少(由于保温层的存在)，热流密度接近于零，导致整个塔体的温差(ΔT)逐渐减小，因此在计算时间内，随时间的增大，截面最大等效应力逐渐减小，但等效应力变化不大。

4 塔体热应力分布规律分析

4.1 裙座与塔体焊缝衔接位置应力分析

取裙座与塔体焊缝衔接位置内、外表面环向路径进行热应力计算分析，得出不同时间的裙座焊缝热应力分布规律。

图6示出裙座与塔体焊缝衔接位置应力分布，可以看出，内表面和外表面路径等效应力分布具有较大的不均匀性。内表面最大等效应力为91.79 MPa，外表面最大等效应力为97.46 MPa，最大等效应力为塔体最大屈服强度的30.1%和32.0%，裙座与塔体衔接位置未出现塑性变形。由于塔体壁厚(δ=82 mm)的原因，内、外表面温度分布趋势刚好相反，即内表面波峰位置为外表面波谷位置。此外，内表面应力随时间的增大而逐渐减小，其原因是在升温阶段，塔体内壁在瞬态温度下温差逐渐减小，因此等效应力也逐渐减小;外表面随着温差的增大，等效应力逐渐增大。

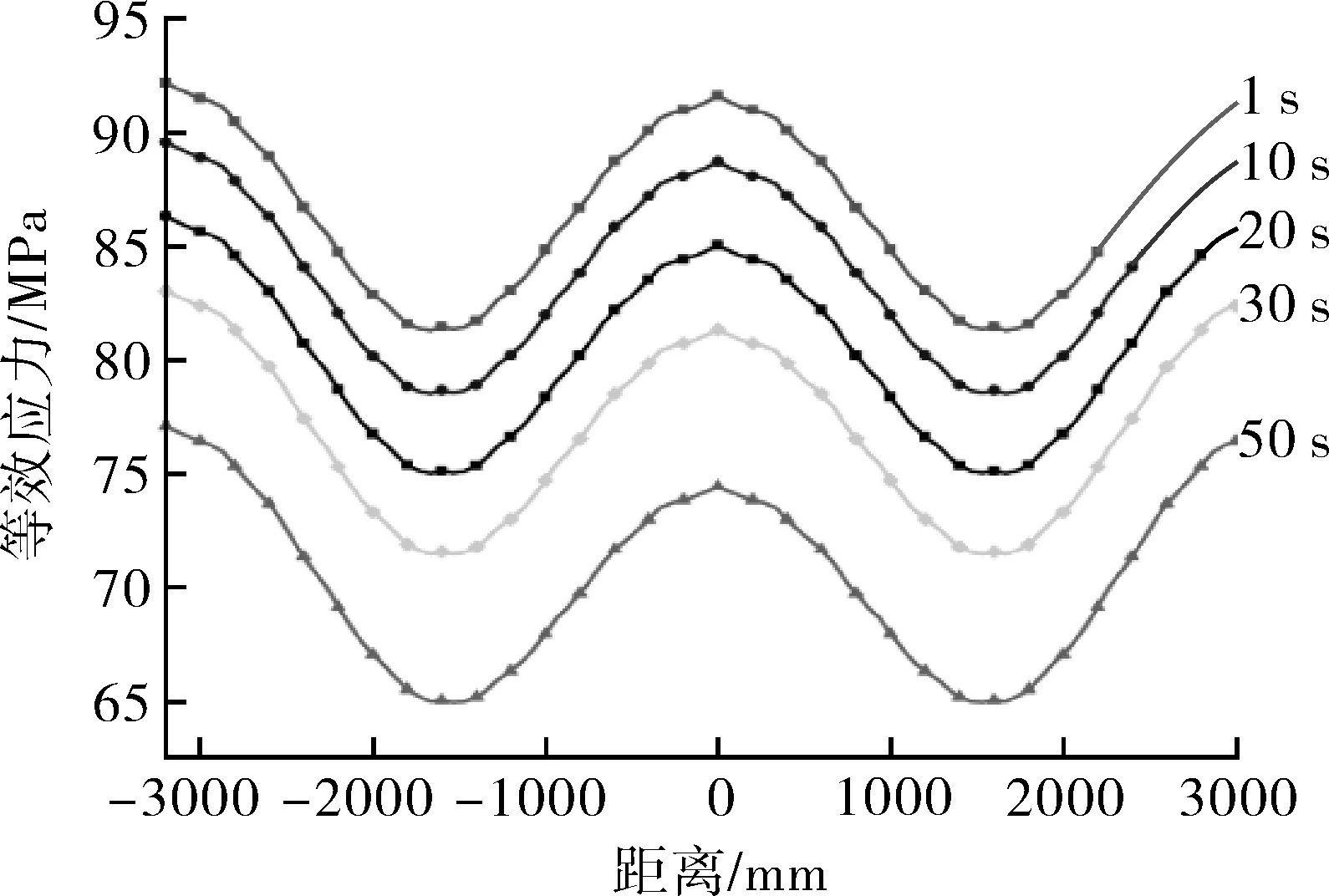
(a)裙座处内表面

4.2 封头与塔体焊缝衔接位置应力分析

分析交变温度载荷下塔体封头与壳体焊接部位应力集中分布规律，取封头与壳体焊缝衔接圆周路径进行应力计算分析，并将计算结果进行对称显示，得出不同时间下的热应力分布规律。

图7示出封头与壳体焊缝衔接位置应力分布，可以看出，不同时间下，内表面和外表面路径上的应力均产生了一定的影响。封头对塔体强度的影响范围较小，内外表面路径上的应力只有靠近开孔位置变化较为剧烈，最大应力为69.32 MPa和67.95 MPa，最大等效应力为塔体最大屈服强度的22.73%和22.28%，未出现塑性变形；随着计算时间的增加，内表面温差逐渐减小后增大；根据热应力基础理论，等效应力先减小后增大；相对于内表面，外表面等效应力增大后减小。

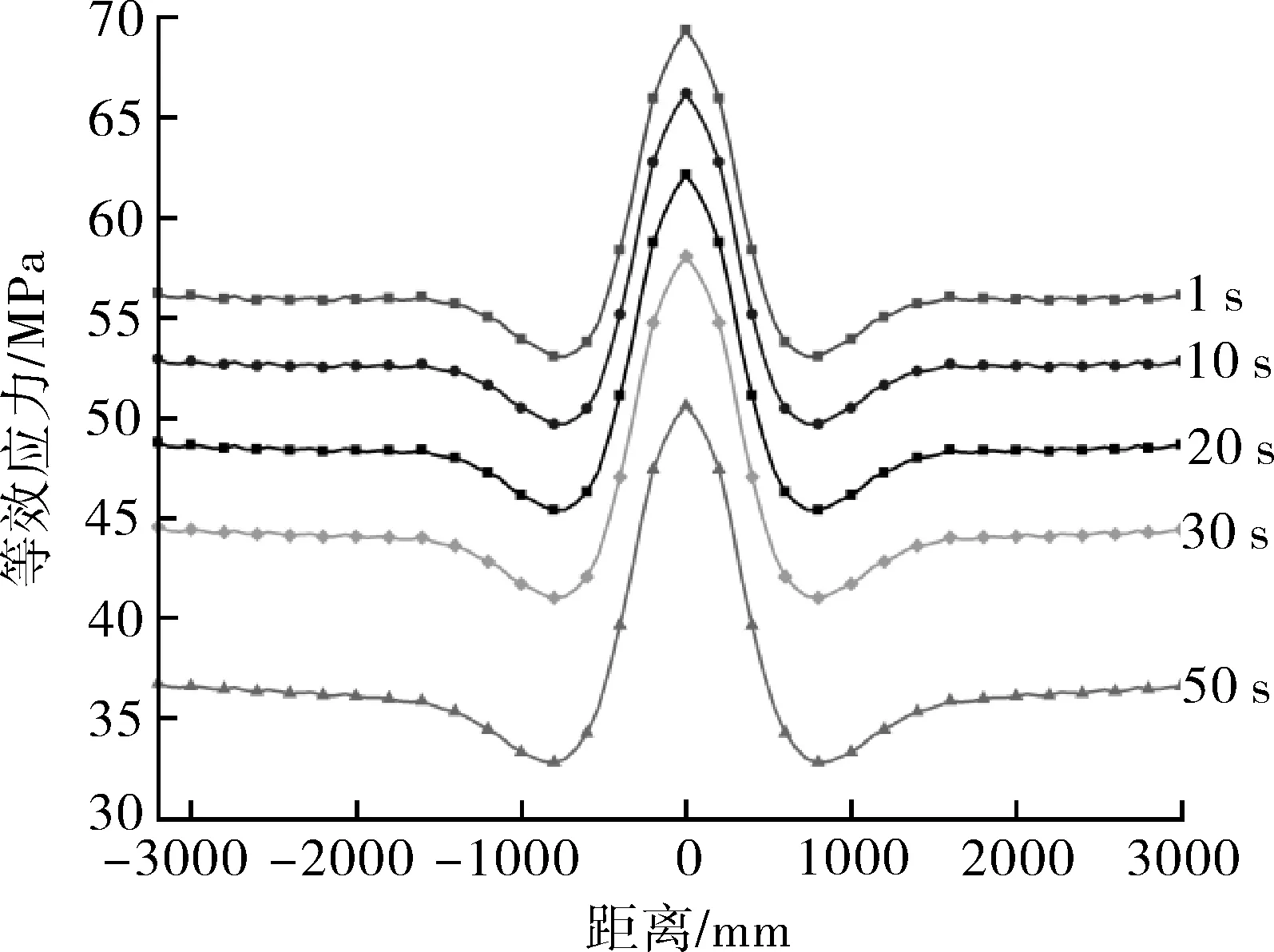
(a)封头处内表面

4.3 焊缝处内外表面应力对比

通过以上分析，裙座、封头和塔体衔接处是反应器的高应力区之一，因此取封头、裙座和塔体焊缝衔接位置内外表面路径(图2(b)路径B-1～B-2和C-1～C-2，路径E-1～E-2和D-1～D-2)进行计算分析，得出不同路径焊缝处的热应力分布规律。分析和比较交变温度载荷下，裙座与塔体焊接部位残余应力分布规律。

图8示出裙座与塔体焊缝衔接位置应力分布。内、外两条路径均呈现不同形态，内表面应力呈现先减小、后增大的趋势，最大值出现在开孔的附近区域；外表面应力呈现先增大、后减小的趋势，最大应力值同样出现在开孔的附近区域。由于内外表面的形变对温度传递具有时差效应，因此，内表面路径上的应力大于外表面路径上的等效应力。

(a)封头内外表面

4.4 接管处应力分布

由图8结果分析表明，应力集中最大位置处于塔体M1和M2开孔接管处，因此本节分析塔体接管位置应力分布状况。取M1，M2开孔接管处圆弧作为路径，选取内表面圆弧两条路径，应力分布如图9所示。

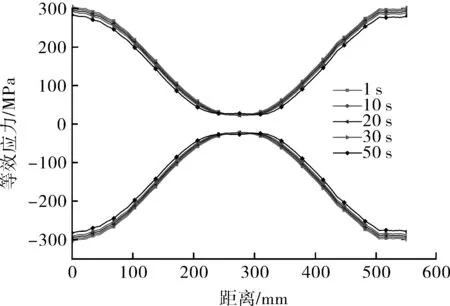
(a)M1接管处内表面

由图9可以看出，接管圆周弧长路径为550 mm，内外表面应力变化趋势基本一致，最大应力达到313.34 MPa和-313.22 MPa(y轴负数表示方向相反)，应力集中系数分别为2.54和2.55；随着时间的延长，等效应力逐渐减小，但减小趋势较为缓慢。

5 应力强度评定

选取应力强度最大受力点，沿壁厚最短方向设置应力线性化路径进行强度评定[17]。线性化路径如图5所示，分别为路径1-1,2-2,3-3。参照JB 4732—1995《钢制压力容器——分析设计标准》进行应力分类和评定校核。由于图5中容器整体部分应力小于123 MPa，仅局部超过123 MPa，所以仅对M2接管连接处进行线性化强度评定，M2处最大交变应力幅为97.5 MPa。接管内壁连接处产生的局部薄膜应力PL为一次应力，局部弯曲应力为二次应力Q，该温度下许用应力限制值为Sm=123 MPa，一次应力限制值为1.5Sm=184.5 MPa，一次应力+二次应力限制值为3Sm=369 MPa，按路径的强度评定结果如表3所示，各评定路径线性化结果均通过评定。

表3 M2接管上路径的应力强度评定结果

进一步按照JB 4732—1995《钢制压力容器——分析设计标准》附录C中图C-1(温度不超过375 ℃的碳钢、低合金钢的设计疲劳曲线)，用弹性模量E=210 GPa对交变应力强度幅Salt进行了修正，修正后的交变应力强度幅S′alt=SaltE/E320=113.14 MPa。根据设计疲劳曲线图的交变应力幅(见表4)，得到S′alt=113.14 MPa时，允许循环次数N>1.0×105次。疲劳强度校核合格，但吸附塔服役时间越长，实际循环次数就越接近许用循环次数，甚至超过许用循环次数，故应定期进行在线监测，防止塔体疲劳失效。