基于改进麻雀算法的工控入侵检测方法*

杨忠君，郑志权，敖 然，王国刚，宗学军，李鹏程

(1.沈阳化工大学 信息工程学院，辽宁 沈阳110142；2.辽宁省计量科学研究院，辽宁 沈阳110006)

0 引言

随着信息化时代的推进，智能信息化技术与各行业不断交叉融合，在带来便捷的同时危险也悄然来临。以伊朗“震网”病毒事件为爆发点，多年来工控安全事件不断出现[1]，已经影响了国家基础建设和民生安全，工业控制网络安全问题已迫在眉睫[2]。

在工业控制网络安全的研究中，入侵检测技术一直是研究的热点。入侵检测的实现机制为根据正常操作行为与攻击入侵行为的模式差别，提取可反映系统行为的深层特征，再通过设计的入侵检测算法对系统行为进行判别分类[3]。领域内学者面向各种工控环境设计出各类检测模型，极大地缓解了工控网络的安全问题。Xue等人[4]设计了一种内部模块为NBI-Net的CNN-SVM模型，分类准确率得到小幅度提升。宋宇等人[5]针对工控系统遭受的ARP攻击设计了一种CNN与BiLSTM结合的混合检测模型。Song等人[6]提出了一种深度卷积神经网络检测方法，通过提取数据的深层特征来提高模型的检测效果。Gu等人[7]为了解决传感器时延误差提出了一种基于粒子群算法(PSO)优化SVM参数来提高检测精度的方法。苏明等人[8]提出了一种基于蚁群算法优化神经网络参数的入侵检测模型，检测性能得到较高的提升。根据以上研究成果可知，多数检测模型的设计核心是如何搭建高精度的分类模型结构，却忽略了如何从原始数据中选取最为合适特征的问题。在入侵检测过程中，针对不同的检测模型和数据样本选取合适的数据特征，会对最终分类的结果有直接影响，并且对数据特征进行约简后将使得算法的计算量呈指数级减小，极大地缩短检测时间。

基于以上成果分析，本文设计了一种利用麻雀优化算法寻优特征子集，并与非线性孪生支持向量机相结合的工控入侵检测方法。通过结合混沌因子和动态权重来平衡算法的全局和局部搜索能力，同时在算法迭代过程中融合对位差分思想和柯西变异因子，对最优解进行扰动，极大程度上弥补了群智能算法易早熟、易陷入局部最优的缺点。本文提出的ISSA-TWSVM入侵检测算法在工控标准入侵检测数据集上与基本麻雀搜索算法和多种经典工控入侵检测模型进行性能对比后，证明了本文算法具有优秀的检测性能。

1 相关内容

1.1 基本麻雀搜索算法

麻雀搜索算法(Sparrow Search Algorithm，SSA)[9]是受自然界麻雀种群的觅食行为的启发而提出的，觅食过程中包含发现者与追随者，并且还加入了危险情景下的种群反捕食机制，随机抽取个体负责侦察警戒。当种群处于危险环境下受到天敌威胁时，则放弃当前觅食，迅速逃生保证自身安全。SSA算法中种群初始位置表示为：

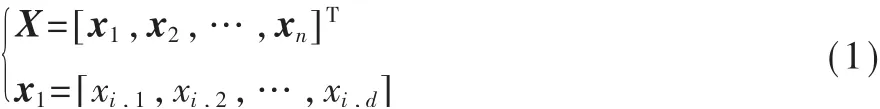
其中d为待优化变量的维数，n为麻雀种群的数量。麻雀的适应度矩阵表示为：

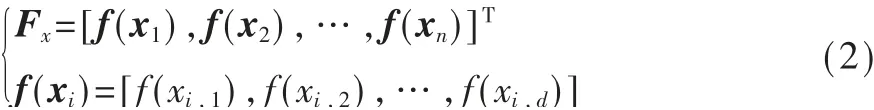
式(2)表示个体的适应度值，在种群初始化后适应度值相对较好的麻雀个体作为发现者带领种群向食物源方向趋近。觅食行为迭代过程中，发现者的位置更新公式如下：

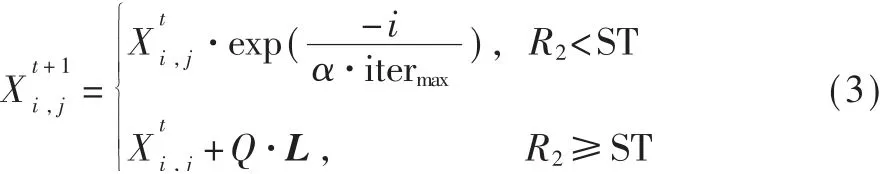
其中，t为当前迭代次数，itermax为最大迭代次数，α∈Random(0，1]，Q是 服 从[0，1]正 态 分 布 的 随 机数，L为1×d的矩阵，R2∈[0,1]与ST∈[0.1，1.0]分别表示预警值和安全阈值。

追随者的位置更新公式如下：

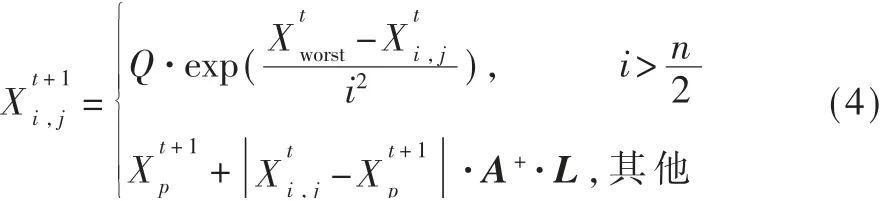
种群反捕食机制中，随机从种群中抽取10%～20%的个体执行侦察警戒任务，其位置更新公式如下：

1.2 孪生支持向量机

孪生支持向量机(Twin Support Vector Machine，TWSVM)作为传统SVM的一种改进方法[10-11]，分别构建正负两个超平面进行数据分类，非常适合处理不平衡的近似类型数据样本，并且容错能力优秀，分类效率高。工控环境下的数据一般都呈现为非线性，因此选取非线性TWSVM为本文入侵检测方法的分类器。

非线性TWSVM的具体实现形式为对式(6)和式(7)优化问题的求解：

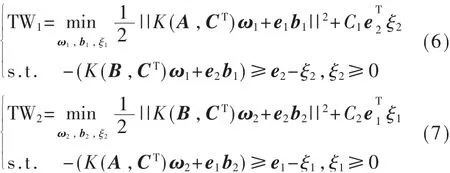
其中K为映射核函数，ω1、ω2为超平面的法向量，b1、b2为超平面偏移向量，C1、C2为惩罚因子参数，e1、e2为 单 位 列 向 量，ξ1、ξ2为 松 弛 变 量。

对上述规划问题求解，TWSVM的两个超平面可以表示为：

因此对新样本分类时，计算其对正负超平面的欧式距离，从而划分判断。超平面分类决策函数为：

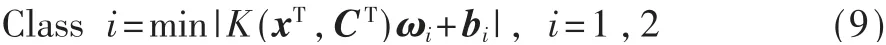
考虑到工控数据的复杂非线性，TWSVM采用的核函数为混合核函数，由Gauss径向基核函数和Sigmoid核函数组成，其数学表达为：

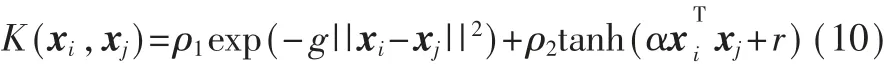
2 改进麻雀搜索算法——ISSA

群智能优化算法领域内的学者研究发现，优化算法迭代初期，由于搜索视野有限，极易陷入局部优值空间[12]。作为群智能优化算法的SSA同样有易陷入局部最优的缺点。对于此问题的解决，本文的ISSA在种群初始化和算法迭代过程中都进行了改进。

2.1 立方映射初始化种群

在种群初始化时，为了扩大搜索视野，引入具有随机性和规律性特点的立方映射混沌算子，映射公式如下：

初始化的麻雀种群由n个d维麻雀个体组成，立方映射初始化的具体实现为：随机生成一个每维变量都处于[-1，1]的d维个体作为起始个体，然后利用式(11)对起始个体迭代得到其余的(n-1)个个体后，使用式(12)将产生的个体映射到麻雀初始种群完成初始化。

其中X′为麻雀个体经立方混沌映射后的初始化种群，y为立方映射向量。

2.2 动态惯性权重

在麻雀算法的发现者位置迭代公式中，考虑到上一代最优解对寻优的影响，引入了动态惯性因子ω动态调整权重系数，使得算法迭代更加贴合求解多维复杂问题中驼峰变化趋势，并且强化了麻雀算法的全局搜索能力。改进后的发现者位置迭代公式如式(14)所示：

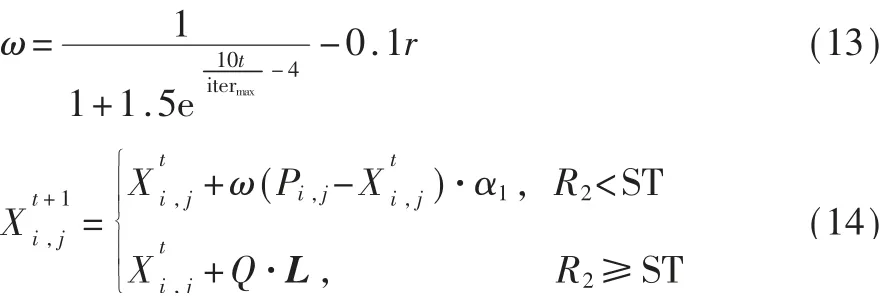
其中，r∈Random(0，1)，Pi，j为上一代全局最优个体位置。

2.3 融合对位差分进化策略和柯西变异算子

差分进化算法[13]是基于遗传算法提出的，而对位差分进化算法[14-15]是差分进化算法的改进。对位差分进化通过对位公式得到对位个体后进行变异杂交操作，从而丰富种群多样性。为了避免算法迭代末期种群多样性降低而导致陷入局部优值空间的问题，本文将对位差分策略融合到SSA算法，在迭代过程中对当前最优解进行扰动，实现过程如下：

生成对位个体：

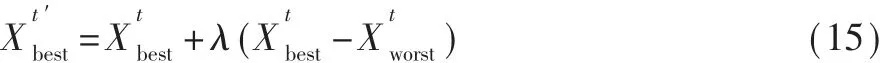
在变异操作中，变异算子选择标准柯西分布函数，使得变异个体具有更广的散布性，进一步丰富种群，公式实现如下：

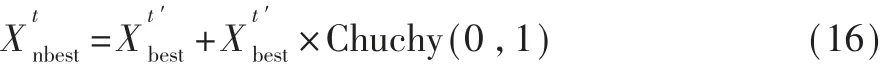
选择操作：

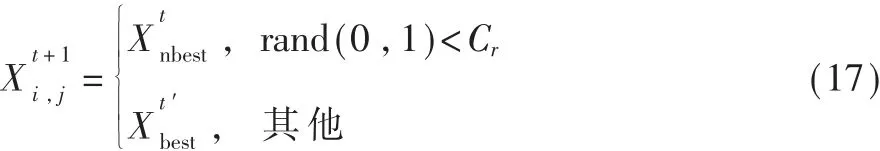
经对位差分进化后的变异个体位置并不一定就优于原最佳个体位置，因而此处本文采用贪婪判断规则，比较二者适应度值，选取适应度值更大的个体位置，来确定更新最优个体位置，公式实现如下：

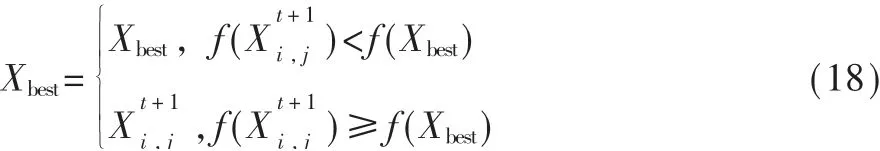
3 ISSA-TWSVM的设计

入侵检测过程中，从原始数据中选取合适的特征是极为重要的环节。对于不同检测分类模型而言，数据特征集合的选取会对检测性能造成直接的影响。在本文提出的入侵检测方法中，首先，采用ISSA算法对工控原始数据的最佳特征子集进行寻优，之后，根据最优特征子集约简数据，最后，利用TWSVM分类器进行工控数据判别。本文模型的适应度函数f(x)为：

其中Acc为TWSVM分类器准确率，x为优化算法中选取的特征个数，allf为原始特征集中的所有特征个数。

本文提出的ISSA-TWSVM工控入侵检测方法的具体实现步骤如下：

Start

(1)以专家标记的所有原始工控数据特征作为原始特征集合，对其进行归一化操作，并采用二进制方式对全部特征个体进行编码。

(2)初始化种群数量n、最大迭代次数itermax等算法参数，并利用式(12)立方混沌映射初始化种群。

(3)计算麻雀个体的适应度值，确定最优、最差适应度值及其位置。

(4)选取部分适应度值较优的麻雀个体作为发现者，并利用式(14)进行迭代。

(5)其余麻雀作为跟随者，并利用式(4)进行迭代。

(6)随机选取10%~20%麻雀个体作为警戒者，并利用式(5)进行迭代。

(7)迭代过程中利用式(17)对当前最优解变异扰动，生成适应度值更好的最优解个体。

(8)根据式(18)判断是否更新最优个体位置。

}；

(9)达到最大迭代次数后，选取种群最优个体。

(10)根据最优个体得到工控数据集的最优特征子集，并对原始工控数据样本进行简化。

(11)使用十折交叉验证在TWSVM分类器上对样本进行判别分类。

End

4 ISSA性能测试

为验证本文改进后的ISSA的优秀性能，以多种经典的群智能搜索算法进行仿真对比。对比算法包括粒子群算法(PSO)[16]、灰狼算法(GWO)[17]、飞蛾火焰算法(MFO)[18]以及基本麻雀算法(SSA)。对比实验基于6个基准测试函数，其中包含单峰标准函数f1~f3和多峰标准函数f4~f6，维度都为30，并且种群数量设置为30，迭代次数都为500次，各自独立运行50次。各优化搜索算法的具体参数设置如表1所示，6个基准测试函数的描述如表2所示。

表1 参数设置表

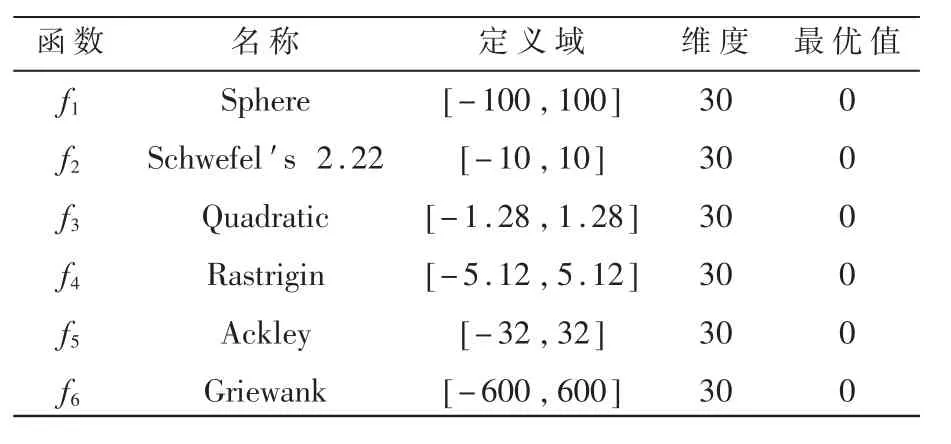
表2 基准测试函数表

由表3分析可知，本文提出的ISSA算法相较于其他经典算法，无论是在单峰标准函数还是多峰标准函数上求解得到的平均值都最为接近理论上的最优解。从多峰函数f4~f6所得的结果可以看出本文的ISSA算法均可以快速地跳出局部最优，求得全局最优解，证明本文在算法改进过程中融合变异扰动的有效性。在标准差方面，本文的ISSA的值最小，说明算法最为稳定，鲁棒性最好。经以上分析说明本文的ISSA相较于其他算法可以更快地寻得最优解。

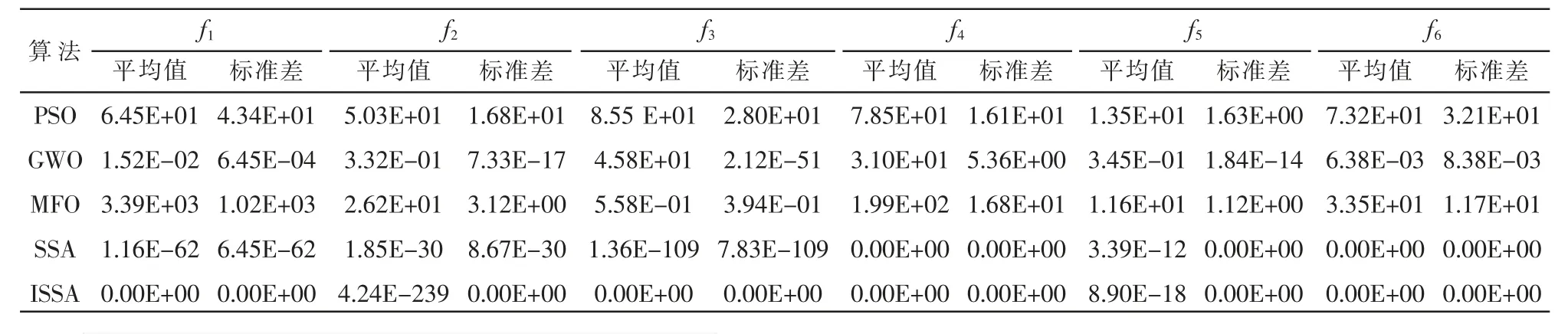
表3 各算法优化结果

图1 (a)～(f)为各个寻优算法分别在6个基准测试函数上测试的收敛曲线。各个子图中的横坐标都代表算法迭代次数，纵坐标都代表适应度的log对数值。从图1可以清楚地看出各个算法的收敛性能的好坏以及跳出局部最优的能力，得出本文的ISSA算法更快达到收敛拐点，曲线更光滑，证明了本文ISSA算法的性能要远优于其他算法。

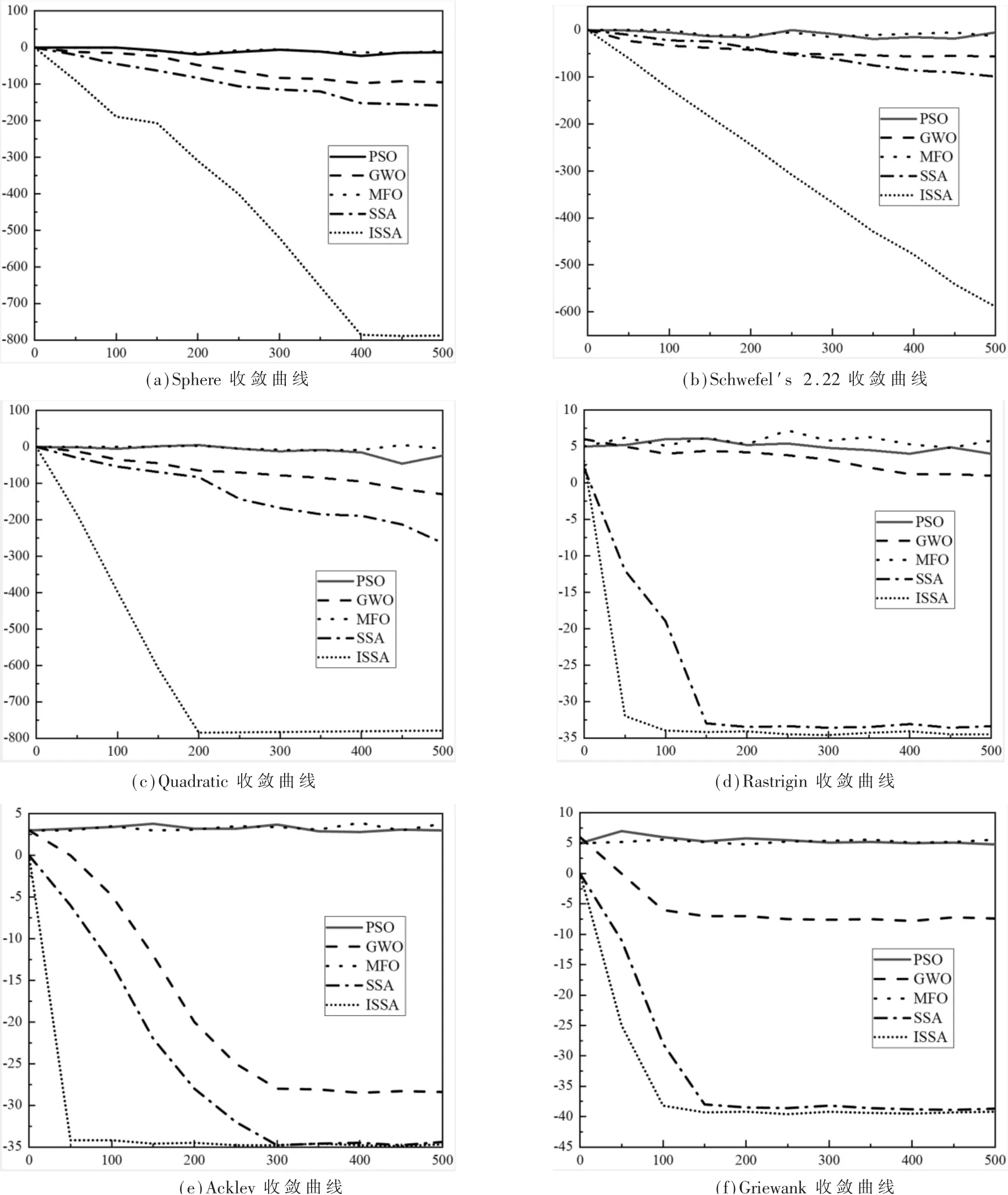
图1 基准测试函数收敛曲线

5 实验及结果分析

本实验运行环境平台配置：计算机CPU为Intel®CroeTMi7-10700 CPU@2.90 GHz，内存为8 GB，NVIDIA GTX 1660 Ti GPU 6 GB，操作系统为Windows 10 64位操作系统。操作实验基于Anaconda Navigator平台下TensorFlow2.0开发框架实现。

5.1 工控数据样本分析

为评估ISSA-TWSVM检测方法在工控网络入侵检测上的性能，本文选取2014年MSU基础设施保护中心建立的工控标准入侵检测数据集，其原始数据是密西西比州立大学内部SCADA实验室设计的天然气管道系统收集的真实数据。数据集是SCADA系统随着时间变化抓取的数据流量，包括35种攻击方式，对应7种攻击类型，26个原始数据特征，是评估工控入侵检测的标准数据集。为了简化实验计算过程，选取10%数据集进行实验，数据类型分布和原始特征如表4和表5所示。

表4 数据集类型分布

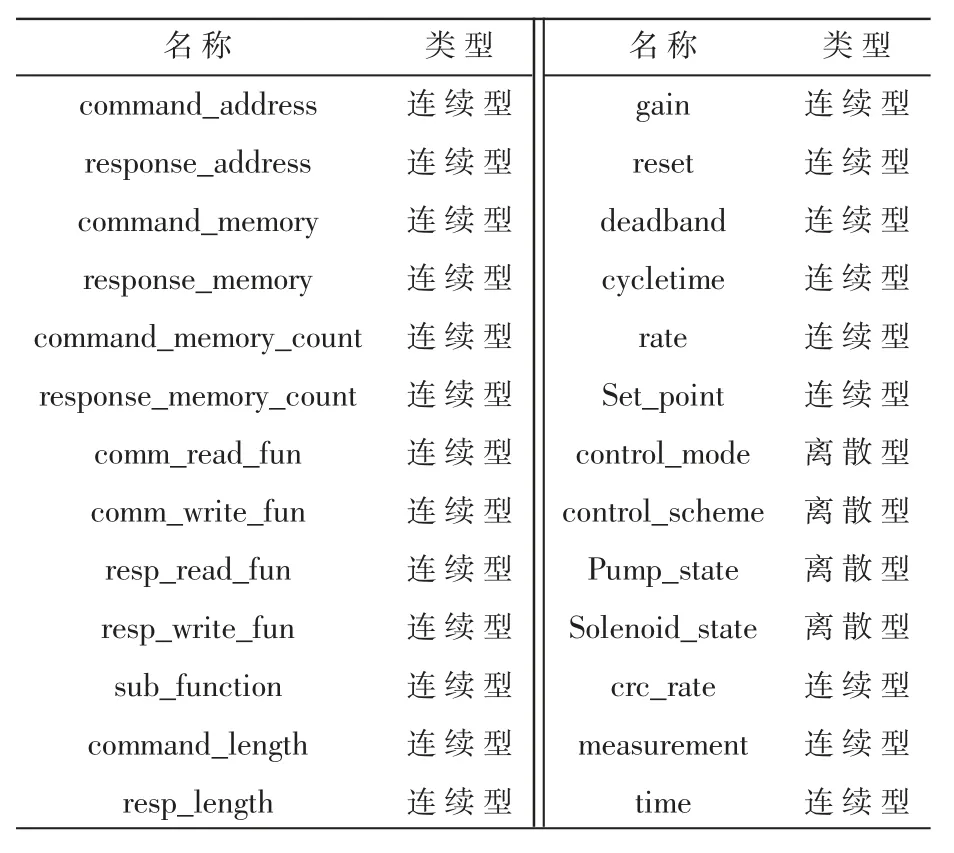
表5 原始数据特征

利用数据集中专家标记的26个原始数据特征组成原始特征集合，进行归一化处理后作为ISSATWSVM算法的输入。为了让实验数据集更贴合实际工控网络环境的流量分布情况，本文使用SMOTE算法[19]对数据集的Normal数据过采样，并对各类攻击数据进行随机均比抽取组成异常数据，重新构造的实验数据分布如表6所示。

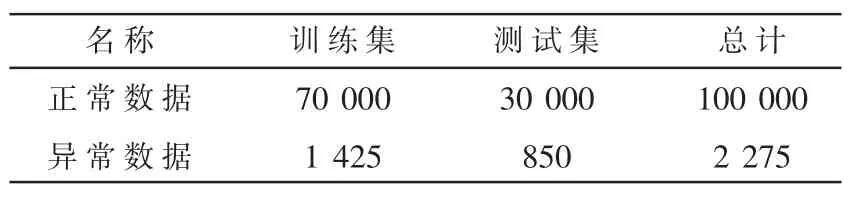
表6 重构数据集数据分布

5.2 评估指标

为了更为直观地与其他入侵检测模型的检测性能进行对比，本文选取评价指标主要有准确率(Accuracy，Acc)以及算法执行时间t。准确率计算公式如下：其中，TP为正确识别的正常数据数量；TN为正确识别的异常数据数量；FP为未正确识别的异常数据数量；FN为未正确识别的正常数据数量。

5.3 实验结果分析

利用基本SSA算法与本文提出的ISSA算法对工控数据的最优特征子集进行寻优，使用TWSVM作为分类器，算法中的适应度函数都设定为式(19)，最终通过最佳适应度个体选取出最优特征子集。实现结果如图2所示。使用SSA算法与ISSA算法对最优特征寻优过程中，随着特征数量的增加，训练所需用时和分类的准确度也随之增加，二者最终都在特征数量为10时达到收敛。对比于基本SSA算法，本文ISSA算法的搜索时间仅为其一半，且在搜索过程中可以看到并未出现陷入局部优值空间的状况，证明了ISSA算法的寻优能力要优于基本SSA算法。

在数据特征选取实验中选取的最佳特征子集如表7所示。

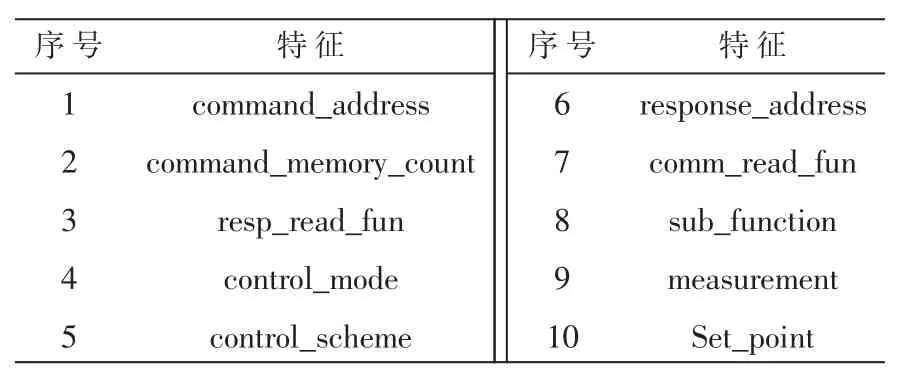
表7 最佳特征子集

为了说明ISSA-TWSVM进行最佳特征子集寻优后的工控网络入侵的检测结果，实验采用十折交叉验证并对各个模型进行30次迭代。选取了基本SSA-TWSVM算 法、SVM算 法[20]、CNN算 法[21]、LSTM算法[22]作为实验对照，各算法实验结果如表8所示。

表8 各算法实验对照

根据表8可知，在准确率上，本文算法分别优于SVM、CNN、LSTM此 类 经 典 检 测 模 型9.26%、4.73%、5.59%，不仅如此，相比于利用基本SSA算法选取特征子集的SSA-TWSVM算法同样要高出2.71%。在执行时间方面，可以看出本文算法遥遥领先，快于SSA-TWSVM算法132.33 ms。由此说明，本文利用ISSA智能优化算法选取最佳数据特征子集后，可使工控入侵检测的检测效率得到大幅度的提升，所以本文提出的ISSA-TWSVM检测方法有着很好的收敛性和检测性能。

6 结论

针对复杂多样的工控入侵数据中的最优特征选择问题，本文提出了一种结合改进麻雀算法和非线性孪生支持向量机的工控入侵检测方法。经本文改进后的ISSA全局和局部搜索能力都得到大幅度提高，将其与TWSVM分类器结合，对工控入侵数据进行检测识别，实验结果证明本文改进的ISSA具有优秀的检测性能且ISSA-TWSVM算法在工控入侵检测中可达到理想效果。