在施工项目规划问题中群智能算法的应用研究
2022-01-05李波,王妍
李 波,王 妍
(长春工程学院计算机技术与工程学院,吉林 长春 130012)
0 引言
工程进度控制是当前工程项目管理中的三大控制(质量控制、进度控制、成本控制)之一[1].工程项目的工期和成本一直以来受到项目管理者的重视,其也直接影响到工程的质量,项目的工期和成本存在相互制约、相互影响的关系[2].建设项目规划中最具有挑战性的任务之一就是在考虑最优资源配置和资源平衡的有关问题的同时,最大限度地减少项目总成本和项目的总时间[3].因此,项目规划者需要处理复杂的多变量:时间、成本、资源,3个变量及其不确定性的平衡优化问题就是TCRO问题[4].到目前为止,对工期-成本优化问题的求解方法有很多,传统的线性规划方法是一种运用较为成熟的优化方法,具有计算方法简单、求解速度较快的优点[5].但是在实际的应用过程中,存在计算误差大、精度较低的缺点,也限制了其在解决实际问题的应用.随着计算机技术以及人工智能技术的不断进步,人工智能优化算法也被广泛运用到项目工期-成本优化问题上,主要有禁忌搜索法(TS)、模拟退火法(SA)、粒子群算法(PSO)、遗传算法(GA)等[6-13].这些算法具有较快的求解速度,能够较为高效地完成最优解搜索,在一定程度上较传统优化方法提高了最优解的质量,但是上述方法均存在计算时间过长以及容易陷于局部最优等问题,难以应用到实际问题中[14-17].而且由于施工活动中诸多不确定因素的存在,使得施工活动的持续时间具有模糊性[18].因此20世纪90年代以来,对于传统的网络计划方法不能解决工程中不确定因素的问题,模糊技术以它特有的优势被考虑应用到网络计划技术当中[19].将模糊技术引入网络,使原不确定信息有了更好地表达方式,能更好地处理由于环境、风险等影响下的其他不确定的信息[20].本文尝试将遗传算法与粒子群算法相混合,并使用模糊集来表征该混合方法中输入数据的不确定性,即模糊启用混合遗传粒子群算法(HGAPSO算法)来计算TCRO问题.将HGAPSO算法应用在工程实践的实际案例中,并与其他算法运算结果进行了对比.
定义1 考虑一个典型的由N个相关活动A组成的项目计划问题:A1,A2,…,AN,由几种选择来分配S类型的项目资源R1,R2,…,RS来执行活动,每个项目进度用项目资源组合执行活动的时间和成本表示.每个活动的时间、直接成本的值和范围都是基于时间-成本函数的依赖变量,由项目规划人员定义.假设项目计划人员可以选择活动的整个可行时间表的选项集合定义为
Oi(j)=(Ti,Ci(R1,R2,…,RS)i)(j),i=1,2,…,N.
(1)
式中j=1/4 ,1,2,…,Mi,其中Mi是执行活动i的可行配置的总数.
执行这种可行的时间选项和直接成本既可以是离散的也可以是连续的,取决可用于执行活动的替代方案的数量.此外,直接成本取决于每个可行的时间表选项(Oi)中的资源分配,并且基于多个资源的资源数量和固定(在没有计算任何利息或通货膨胀下)单位价格的乘积来计算.TCRO问题只能够考虑有限资源的模式,只有在有限的资源条件得到满足时,才会接受每种活动的时间和成本选择.TCRO模型的流程见图1.

图1 TCRO模型的流程
项目规划人员面对的问题是如何分配项目资源和安排活动,以尽量减少项目总成本和项目总时间,同时保持每日资源限制.因此,项目规划者在这个优化问题中的决策变量是项目活动的开始日期SD1,SD2,…,SDN和执行项目活动的资源分配选项O1,j1,O2,j2,…,ON,jN.假设任何一个活动都不能分裂并且在进行中活动的资源分配保持不变情况下,项目规划者在TCRO问题中的目标函数可以表述为最小化总项目成本、最大限度减少总项目持续时间和资源分配总变化3个目标.
定义2Z1为最小化总项目成本.总项目成本包括执行项目活动的总直接成本和完成项目的间接成本.项目的总直接成本与活动持续时间成正比,间接成本通常被认为等于项目执行总时间中项目的每日固定成本总和,公式为
Z1=min(TC).
(2)
定义3Z2为最大限度减少项目总时间(TD).项目总时间是完成项目活动网络关键路径上的关键活动所需的时间,公式为
Z2=min (TD).
(3)
定义4Z3为最大限度地减少资源分配的总体变化.衡量资源分配变化最常用的指标之一是在整个项目期间使用的资源平方和(SSR).项目规划人员应该尽量减少这一资源,以实现更好的资源调配,公式为
(4)
式中Resourcen,k是在n个活动项目持续时间的第k天计划使用的资源的数量,其中n=1,2,…,s,k=1,2,…,TD.
建筑项目规划中的TCRO问题受到以下几个限制:
(1) 项目活动网络图中所示的项目活动之间的逻辑依赖关系.项目活动之间的开始-开始,开始-结束,结束-开始以及结束-结束关系必须在活动开始日期SD1,SD2,…,SDN和相应的持续时间T1,T2,…,TN中.
(2) 每日资源总量限制.整个项目活动中特定资源的总消耗量不得超过项目期间任何时间点该资源的能力.
1 问题建模
在PSO的精英集中,增强的精英是新一代人口的一半,而另一半则是通过对这些增强型的精英进行交叉和变异操作而产生的.HGAPSO作为一种演化学习算法,在可行解空间内生成解,并通过GA的交叉和变异操作,搜索和改进当前解,模糊逻辑已被广泛应用于作为表征建设项目规划中不确定变量的一种方法,通过使用模糊输入数据使算法适用于建筑工程规划的特定环境.本文中使用标准的三角模糊隶属函数来描述完成其中某一项活动的成本和时间的不确定性.
定义5 分配选项集中的成本及时间的最小值、平均值和最大值分别设为Cmin,CavgCmax以及Tmin,Tavg和Tmax.构造三角成本时间隶属函数见图2.
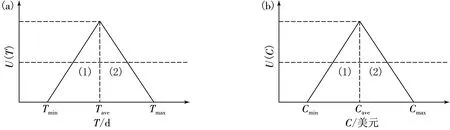
设计用于解决TCRO问题的HGAPSO算法包括以下步骤:
(1) 首先,设置k=1,初始化一组可行的项目进度解决方案为
是整个可行的日期和时间-成本-资源分配活动的随机选择,其中i=1,2,…,N.
该初始人口集由N个项目进度表的解决方案组成,这些方案从项目活动的可行开始日期和时间、成本、资源分配中随机抽取,并且考虑了项目活动之间的逻辑和时间关系.
(2) 计算P(K)中每个可行项目进度计划选项的优化目标函数值为总项目成本(Z1)、总项目持续时间(Z2)和资源分配总变化量(Z3).
(3) 从可行集合P(K)中消除主导解决方案.主导解决方案是一种花费成本、持续时间和资源变化都大于或等于另一种解决方案.从最初P(K)中删除主导的项目进度表选项并更新.
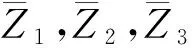
(5) 对于P(K)中的每个项目时间表选项,计算三维客观空间中距离原点的归一化距离,公式为
(4)
(6) 从P(K)的最大距离到最小距离制定项目进度表,将排序的总体集合拆分为两个解集子集:下半部分和上半部分(如果P(K)的大小是偶数,则上半部分子集包括中点).
(7) 应用GA的组合交叉和变异算子详细描述当前的下半部分子集,以生成新的、可行的项目进度表解决方案.这些新的解决方案属于由P(K+1)表示的下一代人口集合的项目进度选项.
(8) 对PSO详细描述当前的上半部分子集,以生成新的、可行的项目进度表解决方案.这些新的解决方案也属于由P(K+1)表示的下一代人口集的项目进度计划选项.
(9) 重复步骤(2)到步骤(8),直到执行步骤(7)和步骤(8)不能找到新的项目进度表解决方案,即当下一代人口组的项目进度计划选项等于当前的一组项目进度计划选项时,并且最终的人口集表示TCRO问题的Pareto最优项目进度计划解决方案.
图3总结了上述步骤,从初始人口到精英人口再到新人口迭代的全部过程.
将使用HGAPSO算法来解决建设项目规划中的实际TCRO问题的案例,从研究方法中找到的最优项目解决方案并与现有优化算法的结果进行比较.
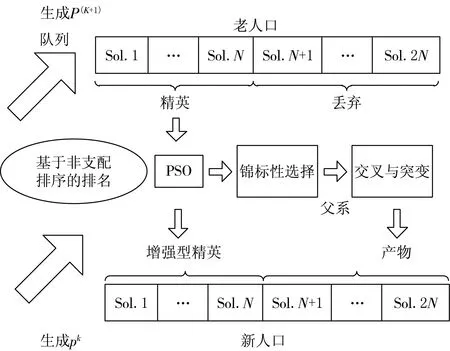
图3 HGAPSO算法的框图
2 案例分析
案例分析1 第1个例子由7个相互关联的活动组成的项目,活动节点图(AON图)如图4所示.本项目使用R1,R2,…,R77种资源类型,每个活动有若干个选项可以使用这些资源的不同配置.表1显示了活动(1)的11个执行活动的时间、资源和成本配比.此外,假定该项目的间接成本为每天1 500美元.
文献[2]使用模糊GA算法来解决这个项目规划问题,并找到最优的项目进度解决方案,并且在2009年应用NSGA-Ⅱ演化算法找到项目进度解决方案的Pareto最优前沿.图4展示了该项目第一项活动的时间和成本函数.
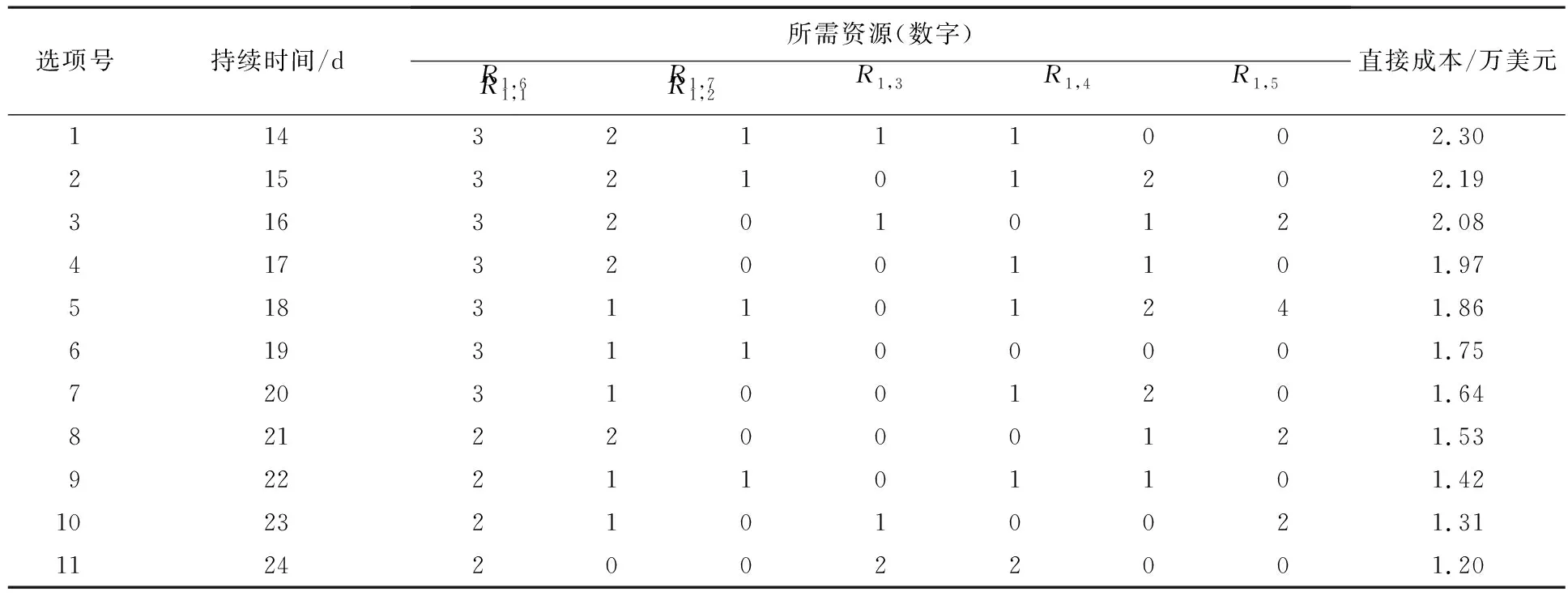
表1 例1中活动(1)的可行项目进度表选项
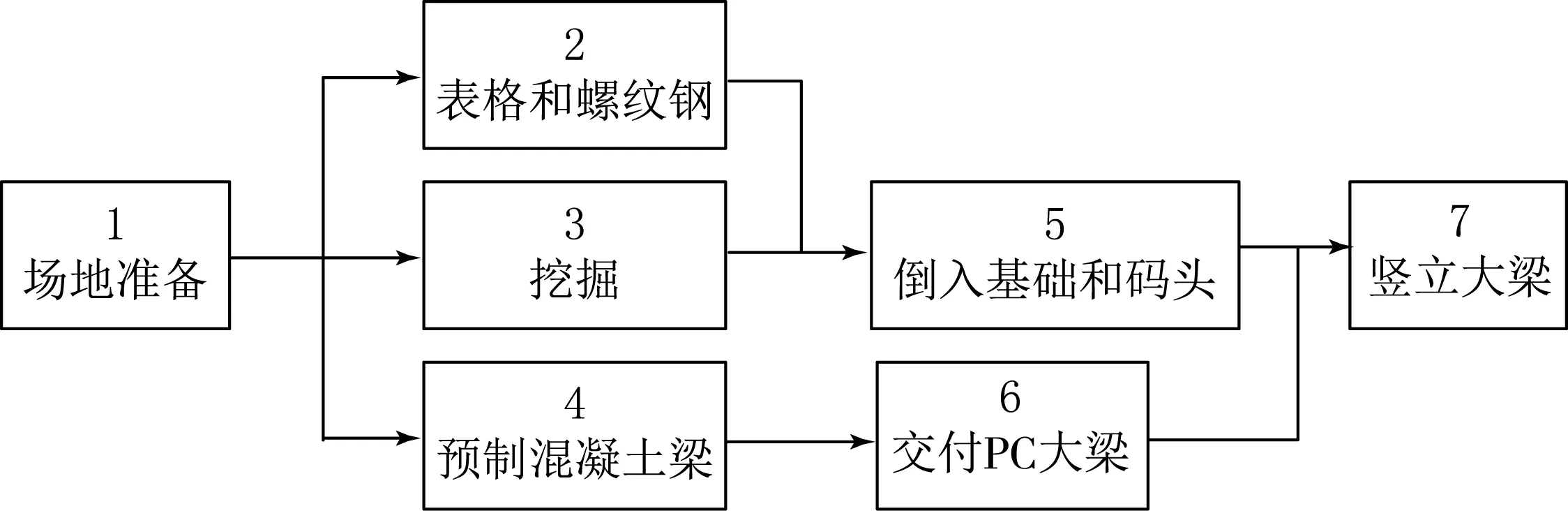
图4 例1中项目活动的AON图
本文也在同一问题中用HGAPSO算法解决这个项目规划问题,以找到项目进度解决方案的Pareto最优解,然后将本文的解决方案与前两种算法的结果进行比较.
活动的持续时间和直接成本的离散化隶属函数见图5.将HGAPSO算法与HGA和NSGA-Ⅱ算法进行比较(见图6),考虑同时最小化总项目成本、总项目持续时间和资源分配的总变化.可以看出HGAPSO算法比HGA算法得出更多的最优解,比NSGA-Ⅱ算法最优解的总项目花费更低.
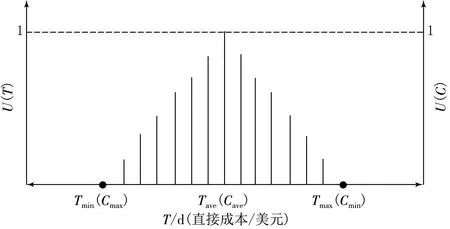
图5 活动的持续时间和直接成本的离散化隶属函数
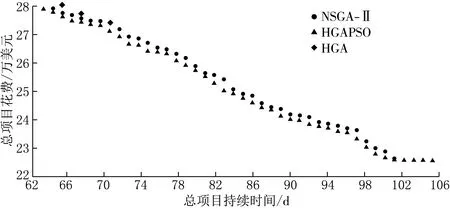
图6 项目总成本和项目工期的2D空间中的最优项目进度解
项目目标三维空间中Pareto最优前沿的项目进度解决方案中项目总成本、总项目持续时间和资源分配总变化见图7,这些Pareto最优点显示了总项目成本,总项目持续时间和非主导项目进度解决方案的资源分配总变化,可以看出在3个目标前提下,在三维图中能够找到本案例的最优解(图7两图资源配比不同).
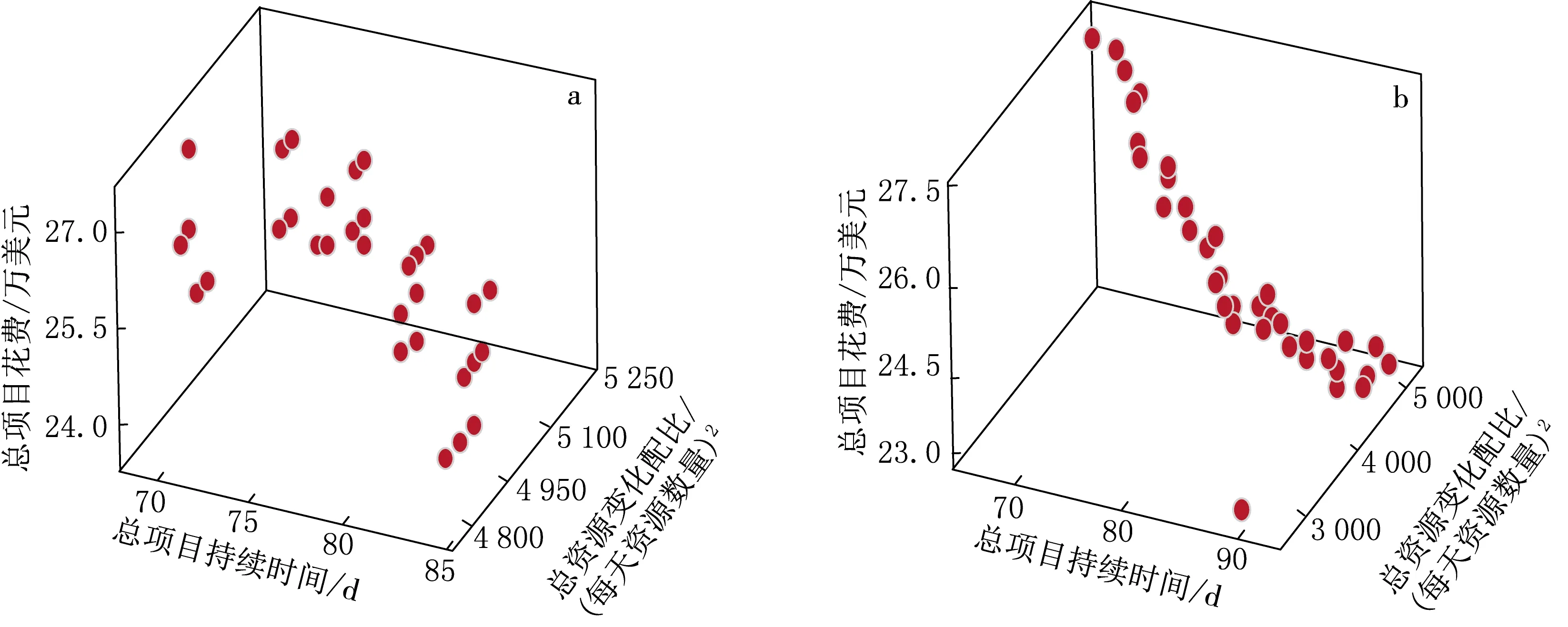
a:资源配比1;b:资源配比2
为了更好地比较这两种算法在项目规划的目标二维解空间中得出的最优项目进度计划解决方案,在解空间中两两目标进行比较:总项目成本和总项目持续时间之间(及C与T之间),总项目成本和总资源分配变化之间(C与R之间),项目总时间和资源分配总变化之间(T与R之间)(见图8).
从图8可以看出,对于总项目成本和总项目持续时间这两个目标而言,相对于NSGA-Ⅱ算法、HGAPSO算法在相同时间条件下,找到的解总项目花费更低;对于同样的总项目花费而言,HGAPSO算法消耗的总资源最少;对于同样的总持续时间而言,HGAPSO算法找到更多最优解,并且消耗资源较少.尤其在图8a中可以找到64 d的最优解,在NSGA-Ⅱ中没有找到;HGAPSO算法发现的最低项目总成本(227 250美元)低于NSGA-Ⅱ算法(228 750美元).在图8b中HGAPSO算法发现的资源分配总量变化最小.

图8 二维解空间两种算法的对比
案例分析2 第2个例子是一个快餐店项目,由14个相互关联的活动组成.该项目还使用了10种不同的资源类型:R1,R2,…,R10,考虑可行资源、时间和成本的各种组合,有几个项目进度计划选项可以执行每项活动.表2中的几个不同的连续和离散的时间-成本函数描述了项目进度选项,每个活动都可以使用不同的资源集合进行.表3总结了执行活动(1)的资源配置的几个示例,每个资源配置对应确定的特定时间-成本配置.该项目的间接费用设定为600美元/d.

表2 案例2中执行项目活动的成本-时间函数
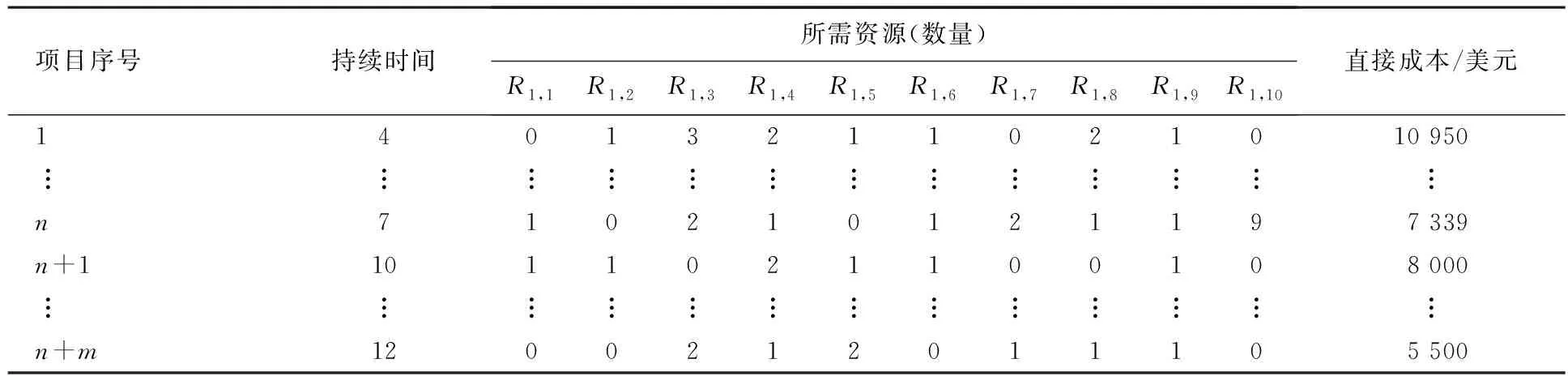
表3 案例2中执行活动(1)的可行项目时间表选项示例
有学者使用PSO算法来解决过这个项目调度问题,并找到了最优的项目进度解决方案.此外,在2009年也将NSGA-Ⅱ算法应用于此问题中寻找最佳项目进度表选项,相比较用HGAPSO算法来解决这个优化问题,能找到更多项目进度解决方案及Pareto最优解.在项目总成本和总项目时间的二维空间中针对该问题的Pareto最优项目进度解决方案见图9.图9显示了HGAPSO、PSO以及NSGA-Ⅱ算法找到的解决方案的总项目成本和总项目持续时间对比.可以看出,HGAPSO算法能够找到更多解决方案,其总项目成本和总项目持续时间较低.尤其是HGAPSO算法所找到的最优解(21 d)的最短总项目持续时间少于PSO算法(27 d)和NSGA-Ⅱ算法(36 d).HGAPSO算法发现的最低项目总成本(81 265美元)低于PSO算法(93 156美元)和NSGA-Ⅱ算法(96 708美元).在本案例中HGAPSO算法以较低的项目总成本和较短的总项目时间寻找额外的最优项目进度解决方案.

图9 项目总成本和项目工期的2D空间中最优项目进度解
3 结论
综上所述,在两个案例中得出以下结论:
(1) 相比于NSGA-Ⅱ算法和PSO算法,HGAPSO算法能找到更多最优解;
(2) 在总持续时间相同的前提下,HGAPSO算法总项目花费时间更低;
(3) 在总花费相同的前提下,HGAPSO算法总资源数量更小;
(4) 在总持续时间相同前提下,HGAPSO算法需要总资源数量更少.
因此,本文在建设项目TCRO问题求解中,HGAPSO算法比NSGA-Ⅱ算法和PSO算法有明显优势.
