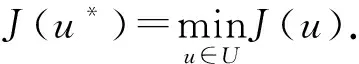中性技术进步条件下的经济控制模型的最优控制分析

孔凡亮，付丽娜，徐加波

(1.新疆工程学院数理学院，新疆 乌鲁木齐 830023；2.新疆工程学院信息工程学院，新疆 乌鲁木齐 830023)

0 引言

宏观经济模型研究从美国学者穆尔进行劳动力市场分析开始到现在已经有近一个世纪的历史了.对宏观经济模型的研究，引起了众多学者的广泛关注.文献[1]从系统学观点出发，把投资—生产—分配—消费等社会生产过程作为一个系统来讨论，并引入了Cobb-Douglas生产函数，建立了宏观经济中的投资—生产—再投资过程的发展模型，研究了该方程的解的存在唯一性及稳定性.文献[2]以希克斯中性技术进步生产函数为反馈要素建立了如下资产发展方程：

其中：Ω=(0，am)，Q=Ω×(0，T)，p(a，t)为t时刻资产存量按役龄a的分布密度函数，μ(a，t)为t时刻资产存量按役龄a的相对折旧率，p0(a)为初始时刻资产按役龄a的分布密度函数，γ(t)为t时刻生产性积累率，A(t)为t时刻综合要素生产率，L(t)为t时刻劳动力函数.文献[3]研究了一类带有时滞的固定资产投资系统的积累率的最优控制问题.文献[4]利用Banach空间理论和Banach-Saks-Mazur定理讨论了一类非定常经济系统资产相对折旧率的最优控制问题.文献[5-7]对资产投资系统的最优控制问题进行了研究，但此类研究还比较少.

许多学者致力于关于具有年龄结构的种群动力系统的最优控制问题的研究[8-18]，对非线性系统的控制问题的研究所引进的方法很有参考价值.

受上述文献的启发，本文研究投资系统关于资产外资的控制问题，并利用中性技术进步生产函数的性质，研究如下一类非线性经济控制模型的最优控制问题：

(OH)

其中：p0(a，t)为某一给定的理想资产分布密度函数；控制变量u∈U={u∈L∞(QT)|0≤u(a，t)≤L，a.e.(a，t)∈QT}，QT=(0，am)×(0，T)，am，T∈(0，+∞)；pu(a，t)满足

(1)

1 系统(1)解的性质

为方便讨论，本文作如下假设：

(H2)γ(t)，A(t)∈L∞(0，T)，0≤γ(t)≤γ，0≤A(t)≤A，a.e.t∈(0，T)；

(H3)p0(a)∈L∞(0，am)，p0(a)≥0，a.e.a∈(0，am)；

(H5)u∈U={u∈L∞(QT)|0≤u(a，t)≤L，a.e.(a，t)∈QT}；

(H6)p0(a，t)∈L∞(QT)为给定理想资产分布密度函数.

定义1.1 所谓系统(1)的解是指存在函数p(a，t)∈L∞(QT)在每一条特征线a-t=k(常数)上绝对连续，且满足

应用特征线法[9]可将系统(1)的解表示为

(2)

其中：

为了得到系统(1)的解，首先给出以下引理：

引理1.1 假设(H1)—(H5)成立，设任意给定T>0，p(a，t)∈L∞(QT)，则p(a，t)是系统(1)的解，当且仅当它是问题(2)的解.

引理1.2 假设(H1)—(H5)成立，如果对任意给定T>0，p(a，t)∈L∞(QT)是问题(2)的解，那么：

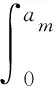
(2)φ(t)≤γAH(amt‖u‖L∞(QT)+am‖p0‖L∞(0，am))eγAHt，a.e.t∈(0，T).

证明

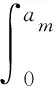
由Gronwall不等式可得

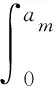
从而

φ(t)≤γAH(amT‖u‖L∞(QT)+am‖p0‖L∞(0，am))eγAHt.

不失一般性，本文假定T>am.记V=L∞(QT)，对任意给定的p∈V，定义算子K(p)(a，t)如(2)式的右端，即

(3)

其中：

令：

M1t=(amT‖u‖L∞(QT)+am‖p0‖L∞(0，am))eγAHt，

M2t=max{γAH(amT‖u‖L∞(QT)+am‖p0‖L∞(0，am))eγAH(t-a)，‖p0‖L∞(0，am)}+T‖u‖L∞(QT)，

W={p∈L∞(0，T|L1(0，am))；p(a，0)=p0(a)，‖p(·，t)‖L1(0，am)≤M1t，0≤p(a，t)≤M2t，a.e.(a，t)∈QT}.

易知W是V的闭子集.

(4)

证明首先对任意p∈W，t∈[0，T]，由引理1.2可得K(q)∈W.

其次对任意p1，p2∈W，t∈[0，T]，由(3)式可得

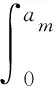
由Gronwall不等式得

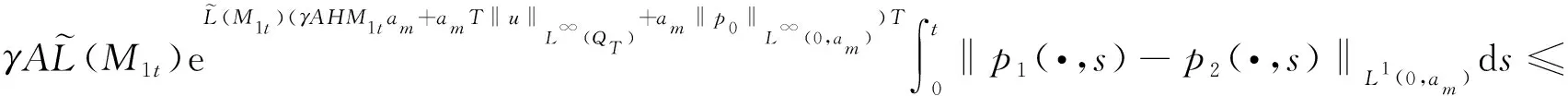
定理1.1 假设(H1)—(H5)成立，则对任一给定的u∈U，系统(1)存在唯一的非负解pu∈L∞(QT)，它关于u一致有界且满足pu(a，t)≤M2T.

对任意p1，p2∈W，由引理1.3知

所以算子K是完备子空间W上的严格压缩映射，由Banach不动点定理可知算子K在W上有唯一不动点，从而问题(2)有唯一非负解.再由引理1.1可知系统(1)有唯一非负解pu∈L∞(QT)，且由引理1.2可得其关于u一致有界并满足pu(a，t)≤M2T.

2 最优解的存在性

考虑下面控制问题解的存在性：

(OH)

其中pu(r，t)是系统(1)的解.

为了求解问题(OH)，借鉴文献[3]的方法，先考察其等价形式.令

U1={p(a，t)|存在u(r，t)∈U，使得p(a，t)是系统(1)的解}.

引入新的性能指标泛函

于是问题(OH)就等价于寻找p*(a，t)∈U1，使得

(OH)′

引理2.1 函数集{Nu|u∈U}在L2(0，T)中是相对紧的.

证明由于pu为系统(1)的解，故对充分小的ε>0，设

则当t∈(0，T)时，Nu，ε(t)是下列微分方程的解：

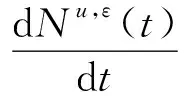
下面利用L2(0，T)空间相对紧定理[8]，证明集合{Nu，ε|u∈U}在L2(0，T)中是相对紧的.由于Nu，ε关于u∈U一致有界，只需验证以下两个条件：

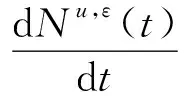
从而引理结论成立.

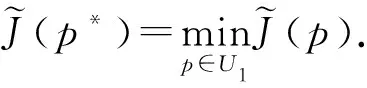
pn在L2(QT)中弱收敛于p*.

(5)

由引理2.1和集合U1的构造，相应地存在Nun的子序列(仍记为Nun)，使得下列关系式成立：

在L2(0，T)中Nun→N*；对[0，T]中几乎处处t，Nun(t)→N*(t).

(6)

(7)

(8)

由(6)和(7)式可得

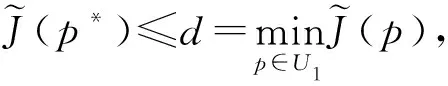
由u(a，t)与p(a，t)的对应关系可得以下定理：