权为1的多项式Rota-Baxter代数的模
2022-01-05吴钇娴唐孝敏
吴钇娴,唐孝敏
(黑龙江大学数学科学学院,黑龙江 哈尔滨 150080)
1 预备知识
Rota-Baxter代数最早出现在20世纪60年代,源于Baxter在概率论中对波动理论的积分方程的代数研究[1].其在代数学中的重要作用,引起了Rota,Atkinson和Cartier等数学家的兴趣,并对其做了深入研究[2-5].近年来,出现了许多有关Rota-Baxter代数的研究结果.[6-12]Baxter[1]在研究涨落理论中的Spitzer等式时引入了一类满足特殊关系式的k-线性算子,称为(权为λ的)Rota-Baxter算子.确切地说,设k是一个含1的交换环,则有如下定义:
定义1.1 设R是一个交换的k-代数,λ是R中的数.若k-线性映射P:R→R满足如下的Rota-Baxter等式:
P(r)P(s)=P(P(r)s)+P(rP(s))+λP(rs),∀r,s∈R,
(1)
则称P是R上的一个权为λ的Rota-Baxter算子.若一个k-代数R带有一个权为λ的Rota-Baxter算子,则称(R,P)是一个权为λ的Rota-Baxter代数.
定义1.2 令(R,P)是权为λ的Rota-Baxterk-代数,设M是一个左R-模,p:M→M是M上的一个k-线性算子,且满足:
P(r)p(m)=p(P(r)m)+p(rp(m))+λp(rm),∀r∈R,m∈M,
则称(M,p)是一个权为λ的Rota-Baxter左(R,P)-模.
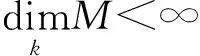
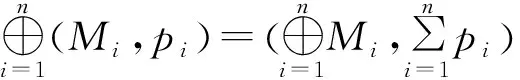
Rota-Baxter代数的模是结合代数的模的推广,近年来才引起学者的关注[9-11].本文将研究权为非零的多项式Rota-Baxter代数模的结构.
注1 若P是k-代数R上的一个权为λ的Rota-Baxter算子,且λ≠0,则易验证λ-1P是一个权为1的Rota-Baxter算子.因此,不失一般性,当研究权为非零λ的Rota-Baxter算子(代数或模)时总假设λ=1.
假设k是特征为零的域.设k[x]是系数取自k且以x为变元的多项式代数.将给出一个权为1的Rota-Baxter代数(xk[x],P),其中P是由k[x]上一类权为1的Rota-Baxter算子限制得到的[12].
定义1.3 在xk[x]上定义线性算子P,其作用确定为
P:xk[x]→xk[x],P(xm)=-xm,m∈N+,
其中N+为所有正整数构成的集合.则易知(xk[x],P)是一个权为1的Rota-Baxter代数.本文以下所说的多项式Rota-Baxter代数均指此权为1的Rota-Baxter代数(xk[x],P).
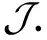
定义1.4 设k〈x,y〉是以x和y为变元的非交换多项式代数,I(x,y)是由多项式xy+yxy生成的k〈x,y〉的主理想.定义商代数如下:
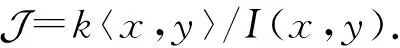
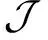
2 多项式Rota-Baxter代数与代数 模
设(xk[x],P)是本文给出的多项式Rota-Baxter代数,即对任意的m∈N+,都有P(xm)=-xm.注意到k〈x,y〉是以x和y为变元的非交换多项式代数,令IP是由集合
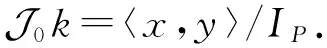
对于任意m∈N+,有P(xm)y-yP(xm)-yxmy-yxm=-yxmy-xmy.由于P是k线性的,因此集合
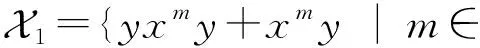
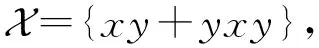

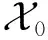
yxm+1y+xm+1y=yxm+1y+yxmyxy-yxmyxy+xm+1y=yxm(xy+yxy)-yxmyxy+xm+1y=yxm(xy+yxy)-yxmyxy-xmyxy+xmyxy+xm+1y=yxm(xy+yxy)-(yxmy+xmy)xy+xm(yxy+xy).
由归纳假设可知yxm+1y+xm+1y∈I(x,y),推出X1⊂I(x,y),于是有IP⊆I(x,y).因此IP=I(x,y).
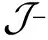
P(f)p(v)=p(P(f)v)+p(fp(v))+p(fv),∀f∈xk[x],v∈M.
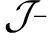
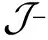
p(v)=yv,∀v∈M,
(2)
则(M,p)是一个(xk[x],P)-模.反之,若(M,p)是一个(xk[x],P)-模,定义
yv=p(v),∀v∈M,
(3)
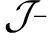
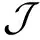
(P(xm)y-yP(xm)-yxmy-yxm)v=P(xm)yv-yP(xm)v-yxmyv-yxmv=0.
将(2)式代入上式可得
P(xm)p(v)=p(P(xm)v)+p(xmp(v))+p(xmv).
因此(M,p)是一个(xk[x],P)-模.
反之,假设M是一个k〈x,y〉-模,(M,p)是一个(xk[x],P)-模.于是,对于任意v∈M,有
(P(xm)y-yP(xm)-yxmy-yxm)v=P(xm)yv-yP(xm)v-yxmyv-yxmv.
利用等式(3),上式等于P(xm)p(v)-p(P(xm)v)-p(xmp(v))-p(xmv),即
IP⊆annM={F∈k〈x,y〉∣Fv=0,∀v∈M}.
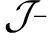
推论2.1 设M是一个xk[x]-模,p∈Endk(M),则(M,p)是一个(xk[x],P)-模,当且仅当
xp=-pxp.
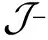
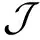
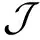
xym=xyym-1=-yxyym-1=-yxym.
由此易知结论成立.
3 多项式Rota-Baxter代数的模的刻画
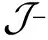
x(e1,e2,…,en)=(xe1,xe2,…,xen)=(e1,e2,…,en)A,
y(e1,e2,…,en)=(ye1,ye2,…,yen)=(e1,e2,…,en)B.
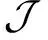
命题3.1 设M是一个xk[x]-模,p∈Endk(M)并设x和p在M的某组基下的矩阵分别为A和B.则(M,p)是Rota-Baxter代数(xk[x],P)的一个模,当且仅当关于A和B的如下矩阵方程成立:
(In+B)AB=0.
(4)
由命题3.1,刻画多项式Rota-Baxter代数(xk[x],P)的模只需解矩阵方程(4).下面给出几个多项式Rota-Baxter代数的模:
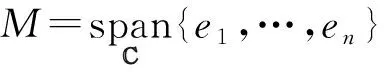
(ⅰ)M∶=M0,θ∶xei=0,p(ei)任意,∀i=1,…,n;
(ⅱ)M∶=Mθ,0∶xei任意,p(ei)=0,∀i=1,…,n;
(ⅲ)M∶=Mθ,-I∶xei任意,p(ei)=-ei,∀i=1,…,n.
证明设x和p在M的基{e1,…,en}下的矩阵分别为A和B.由命题3.1,(M,p)是多项式Rota-Baxter代数(xk[x],P)的一个模,当且仅当(4)式成立,即(In+B)AB=0.注意到M∶=M0,θ恰是A=0的情形,M∶=Mθ,0恰是B=0的情形,而M∶=Mθ,-I恰是B=-In的情形.定理得证.
命题3.3 取定s=(a1,a2,a3,a4,λ2)∈k5.记M为k上的2维线性空间,具有基底{e1,e2}.则M上的线性映射p和x在M上的以下5 种作用分别使得(M,p)是Rota-Baxter代数(xk[x],P)的5种模:
(ⅰ)x(k1e1+k2e2)=k1(a1e1+a3e2),p(k1e1+k2e2)=λ2k2e2,∀k1,k2∈k,其中λ2≠-1,0;
(ⅱ)x(k1e1+k2e2)=(k1a1+k2a2)e1+k2a4e2,p(k1e1+k2e2)=-k1e1,∀k1,k2∈k;
(ⅲ)x(k1e1+k2e2)=(k1a1+k2a2)e1,p(k1e1+k2e2)=-k1e1+λ2k2e2,∀k1,k2∈k,其λ2≠-1,0;
(ⅳ)x(k1e1+k2e2)=k2a2e1+k2a4e2,p(k1e1+k2e2)=k2e1,∀k1,k2∈k;
(ⅴ)x(k1e1+k2e2)=(k1a1+k2a2)e1,p(k1e1+k2e2)=(-k1+k2)e1-k2e2,∀k1,k2∈k.
证明设x和p在M的基{e1,e2}下的矩阵分别为A和B.易见上述5种情形A,B分别如下:
直接验证可知每种情形都有(I2+B)AB=0.由命题3.1可知结论成立.
下面给出Rota-Baxter代数(xk[x],P)的1维和2维模的刻画.
定理3.1 设(M,p)是一个1维Rota-Baxter代数(xk[x],P)的模,则M必为命题3.2给出的3种模之一,即:M0,θ,Mθ,0,Mθ,-I.
证明设x和p在M的基{e1}下的矩阵分别为a和b.由命题3.1,(M,p)是Rota-Baxter代数(xk[x],P)的一个模,当且仅当
(b+1)ab=0.
注意到a,b∈k, 于是由上式可得a=0,或b=0,或b=-1.这导致3种情形:(ⅰ)a=0,b任意;(ⅱ)a任意,b=0;(ⅲ)a任意,b=-1.它们分别对应M0,θ,Mθ,0,Mθ,-I.证毕.
定理3.2 设(M,p)是一个2维Rota-Baxter代数(xk[x],P)的模,则M必为命题3.2和命题3.3给出的8种模之一.
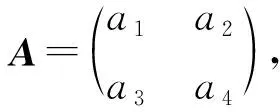
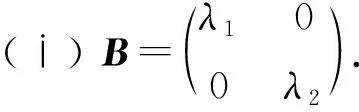
(5)
此时分λ1,λ2∉{0,-1},λ1∈{0,-1}和λ2∈{0,-1}的情形讨论.注意到λ2∈{0,-1}可以通过调换基底元素的顺序归结为λ1∈{0,-1}的情形.因此,共分为以下6种情形:
(ⅰ1) 若λ1,λ2∉{0,-1},则由(5)式可得A=0;
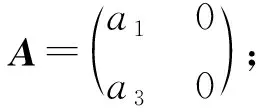
(ⅰ3) 若λ1=0,λ2=0,即B=0,则由(5)式可知A任意;
(ⅰ4) 若λ1=-1,λ2=-1,即B=-I2,则由(5)式可知A任意;
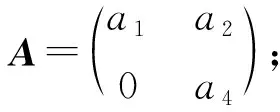
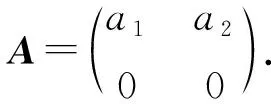
对照可知,(ⅰ1)是命题3.2给出的模M0,θ的一种;(ⅰ2),(ⅰ5),(ⅰ7)分别是命题3.3中(ⅰ),(ⅱ),(ⅲ)给出的模;(ⅰ3),(ⅰ4)分别是命题3.2给出的模Mθ,0,Mθ,-I.
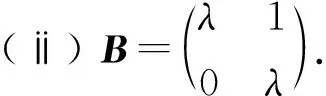
(6)
此时分λ∉{0,-1}和λ∈{0,-1}的情形讨论.
(ⅱ1) 若λ∉{0,-1},则由(6)式可得a3=a4=a2=a1=0,即A=0;

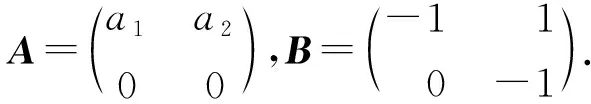
对照可知,(ⅱ1)是命题3.2给出的模M0,θ的一种,(ⅱ2),(ⅱ3)分别是命题3.3中(ⅳ),(ⅴ)给出的模.即结论得证.
