一类半离散可积方程族的无穷守恒律
2022-01-05张艳妮
张艳妮,邢 维,李 雯
(1.吉林建筑科技学院基础科学部,吉林 长春 130114;2.海军大连舰艇学院基础部,辽宁 大连 116013;3.吉林大学数学学院,吉林 长春 130012)
0 引言
可积方程是一类特殊的非线性系统,在物理学、生物学、光学等领域中有着重要的应用.按照变量的不同,可积方程可以分为连续的、半离散的和全离散的.对于可积性,目前还没有严格的统一定义,但普遍认为,可积方程应该具有一对线性谱问题(Lax对),或有非常丰富的数学结构,例如无穷守恒律、无穷多对称、双Hamiltonian结构等.此外,人们发现可积方程普遍存在孤立子解,对可积方程的研究已有很多重要成果[1-4].无穷守恒律是可积方程的一个重要性质,自1968年Miura[1]发现KdV方程的无穷守恒律以来,很多学者尝试给出构造方程的无穷守恒律的方法[5-7].2002年,Zhang等[3]基于Lax对,通过研究Ricatti方程给出了一种行之有效的构造方程无穷守恒律方法.近年来,Fan等[8-9]成功地利用该方法构造了一些方程的无穷守恒律.
迄今为止人们已经发展了多种构造可积方程的方法,如屠格式[10]、AKNS方法[11]等.屠格式不仅可以构造Lax可积的方程族,还可以通过变分、迹恒等式等方法给出Hamiltonian结构和Liouville可积的计算方法.AKNS方法一般从线性散射问题的空间部分出发,展开求解线性散射问题的时间部分,从而得到可积系统.这些构造可积系统的方法为孤子理论和非线性科学提供了丰富的研究对象和内容.
2004年,Xu等[12]考虑了如下离散谱问题:
(1)
其中:φn=(φ1,n,φ2,n)T是特征函数;rn,sn是势函数;λ是谱参数,λt=0.从谱问题(1)出发,利用屠格式构造了一类方程族,并研究了方程族的可积性,建立了相应的辛映射.
2006年,Sun等[13]提出如下谱问题:
(2)
从谱问题(2)出发,利用屠格式构造了正向和负向的可积方程族,建立了对应的耦合可积方程.
基于谱问题(1)和(2),本文将考虑如下广义的离散谱问题:
(3)
从谱问题(3)出发,利用屠格式构造新的半离散可积方程族,并借助Ricatti方程构造法建立无穷守恒律,研究方程的可积性质.
1 预备知识
设fn=f(n,t)是格函数,移位算子E、逆算子E-1和差分算子Δ定义如下:
Ef(n,t)=f(n+1,t)=fn+1;
E-1f(n,t)=f(n-1,t)=fn-1;
Δf(n,t)=(E-1)f(n,t)=fn+1-fn.
考虑半离散方程
un,t=f(un-N,un-N+1,…,un,…,un+M-1,un+M),
(4)
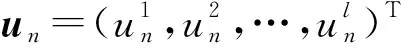
Eφn=Unφn,φn,t=Vnφn
(5)
的相容条件,即Un,t=(EVn)Un-UnVn,则称方程(4)是Lax意义下可积的,称谱问题(2)为方程的Lax对.这里:φn是m维向量函数,被称为特征函数;Un,Vn是m阶矩阵,其元素中包含谱参数λ,un以及un的移位,un被称作势函数.
如果存在标量函数
ρn=ρn(un-m1,un-m1+1,…,un+m2),Jn=Jn(un-r1,un-r+1,…,un+r2),
使得
Dtρn=ΔJn,
(6)
则称(6)式是方程(4)的局部守恒律,ρn和Jn分别称为相应的守恒密度和流.
2 一类新的半离散可积方程族
从广义谱问题(3)出发,通过屠格式构造新的半离散可积方程族.求解如下驻定的离散零曲率方程:
即
(7)
将
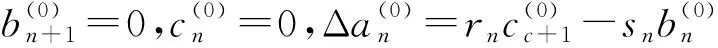
(8)
令
其中“+”表示选取λ的正次幂.利用递推关系(8)式,直接计算得
(9)
不难看出,此时(9)式和Un,tm是相容的.因此,当
(10)
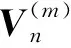
(11)
由(11)式可得到如下新的半离散方程族:
(12)
其中谱问题(3)和(10)构成了方程族(12)的Lax对,即方程族(12)是Lax意义下可积的.
当m=1时,由(12)式可得如下Lax可积的半离散方程:
(13)
Lax对为
(14)
且
(15)
3 无穷守恒律
利用Ricatti方程构造法给出方程(13)的无穷守恒律.根据(14)式得
φ1,n+1=λrnφ2,n,
(16)
φ2,n+1=λsnφ1,n+(λ2+qn)φ2,n.
(17)
由(15)式得
(18)
令Γn=φ2,n/φ1,n由(16)和(17)式知
λrnΓnΓn+1=λsn+(λ2+qn)Γn.
(19)
进一步将(19)式表示为
(20)
假设
(21)
根据(16)和(18)式得
(22)
将(22)式带入恒等式
中,可得
(23)
其中
这里
将Φn和Ψn带入(23)式,对比等式两端λ的同次幂系数,得到方程(13)的无穷守恒律
(24)
其中:
