具有外部扰动分数阶不确定性单摆混沌系统的自适应滑模同步
2022-01-05毛北行王东晓
毛北行,王东晓
(郑州航空工业管理学院数学学院,河南 郑州 450015)
混沌同步自提出以来就备受重视[1-9].分数阶系统在现实世界中大量存在,且用分数阶微分方程建模更符合模型本身的特点,因而随着分数阶微分学与积分学的发展,分数阶混沌系统的同步控制引起了工程科学界的浓厚兴趣.例如:文献[10] 研究了一类分数阶不确定同步发电机系统的自适应滑模控制与参数辨识;文献[11]根据自适应滑模方法研究了一类分数阶不确定系统同步问题;文献[12]研究了一类分数阶不确定混沌系统的自适应滑模同步,获得主从系统达到滑模同步的充分条件;文献[13]研究了不确定分数阶混沌系统的主动滑模同步;文献[14]研究了分数阶不确定系统的有限时间滑模同步技巧;文献[15]研究了不确定分数阶Victor-Carmen系统的滑模同步.另一方面,单摆混沌系统引起了众多学者的高度关注.例如:文献[16]研究了大角度单摆周期的估计;文献[17]研究了重力常数的测定;文献[18]研究了有界扰动下单摆的分岔混沌分析;文献[19]研究了从周期到有界混沌;文献[20]研究了从单摆到混沌的动力学分析与控制;文献[21]研究了单摆混沌现象问题;文献[22]对单摆系统多参数混沌边缘进行了研究,得到了单摆系统产生混沌的条件;文献[23]研究了单摆到混沌的条件;文献[24]研究了一类整数阶分数阶单摆的混沌同步;文献[25]研究了一类分数阶单摆混沌系统的终端滑模同步.虽然来自模型及系统本身的不确定性和外部扰动在工程实际中大量存在,且是系统不稳定和产生扰动的根源,但有关分数阶单摆不确定系统的自适应滑模同步方面的研究还鲜有报道.在上述研究基础上,本文研究了分数阶具有外部扰动和不确定性单摆混沌系统的自适应滑模同步,分别设计了滑模面并证明了滑模面的稳定性与可达性,获得不确定分数阶单摆系统取得自适应滑模同步的两个充分条件.
1 预备知识
无阻尼单摆系统可描述为
(1)
其中:θ为摆线的夹角,L为摆长,g为重力加速度.如图1所示.
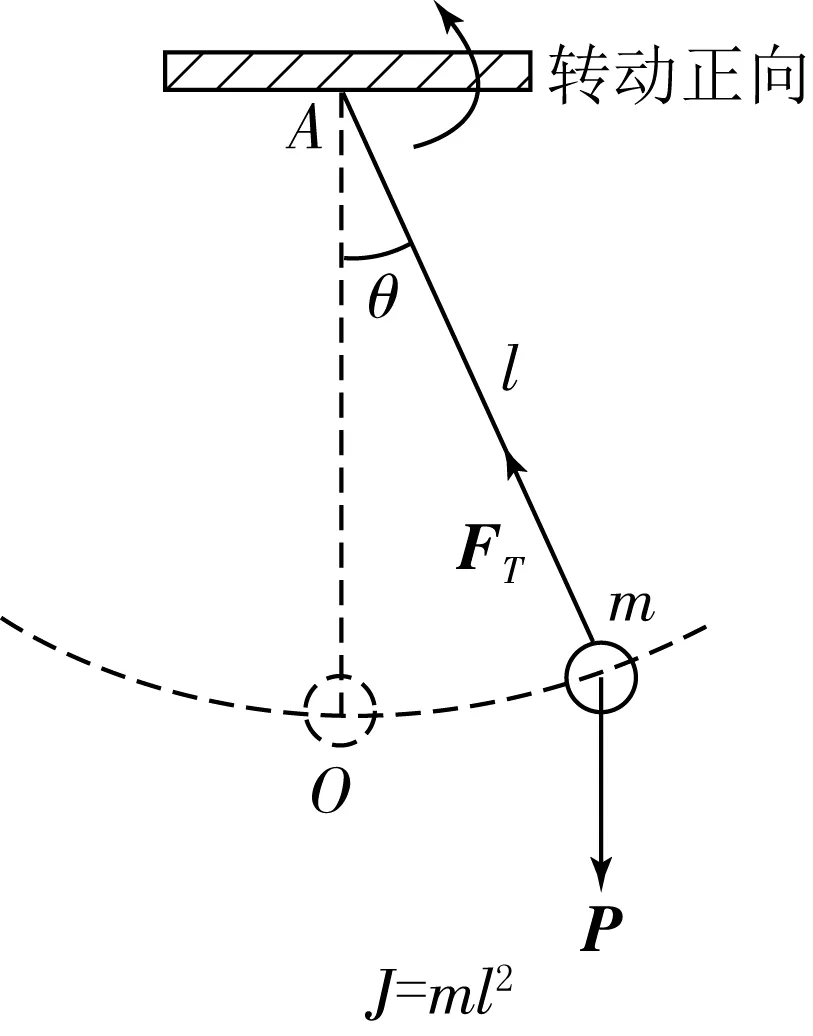
图1 单摆图
考虑阻力,设阻尼系数为γ,则单摆系统可描述为
(2)
其等价系统如下:
主系统设计为
(3)
考虑外部扰动和不确定性,从系统设计为
(4)
这里y(t)=(y1,y2)T,Δfi(y,t)和di(t)分别为有界不确定项和外部扰动,ui(t)为控制器.
定义ei=yi-xi(i=1,2),则
(5)
定义1[26]Caputo分数阶导数定义为
分数阶单摆混沌可描述为
(6)
当g=10,L=1,γ=0.46,q=0.86时,系统呈现混沌态,系统的相图如图2所示.

图2 单摆系统相图
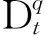
(7)
假设1 不确定项Δfi(y,t)和外部扰动di(t)均有界,即存在未知常值参数mi,ni>0,满足
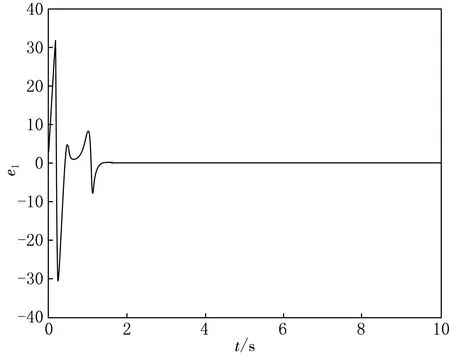
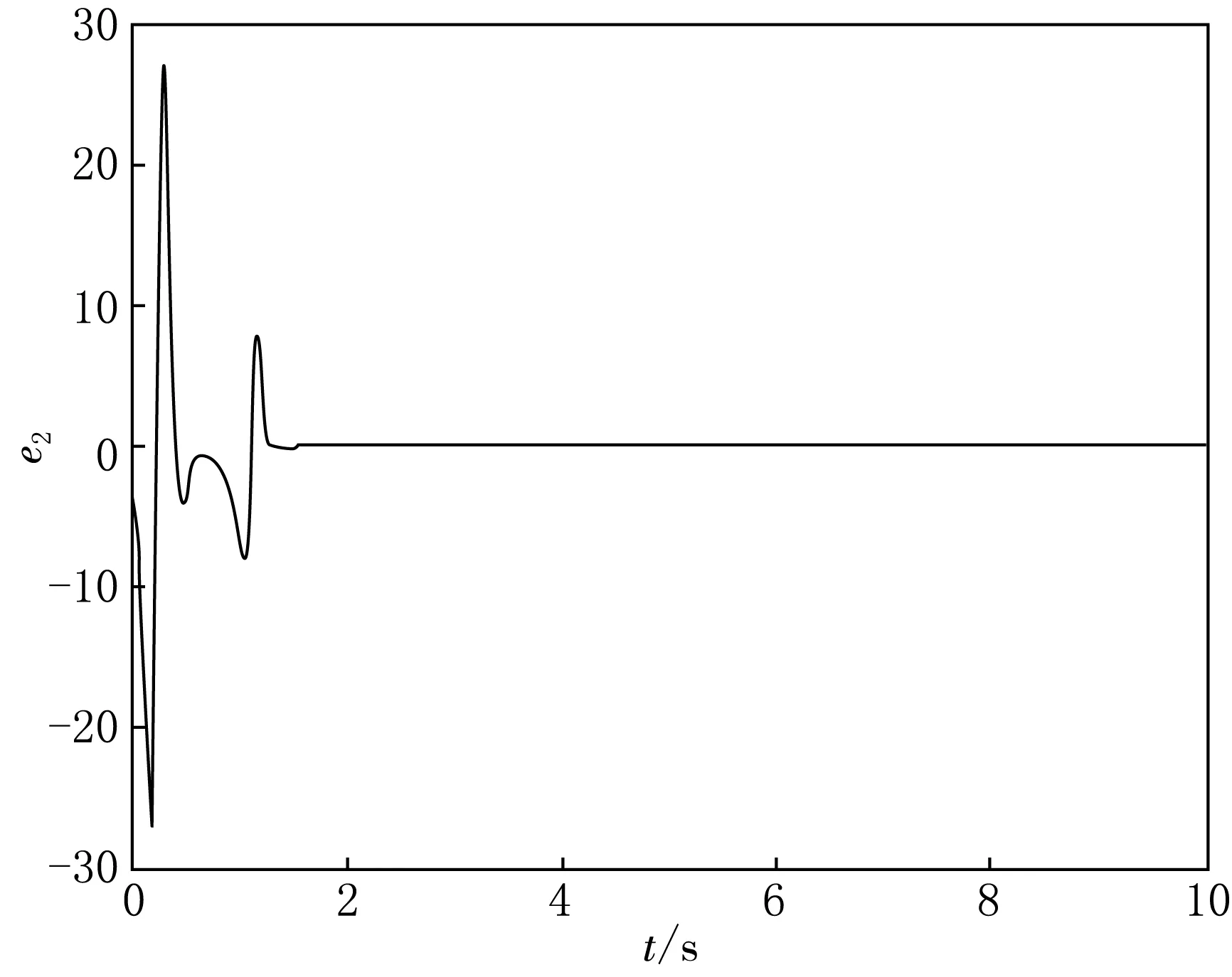
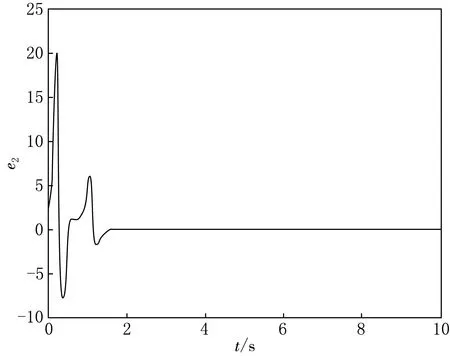
|Δfi(y,t)| 定义ei=yi-xi,i=1,2,则 (8) 用引理2,得到si→0⟹ei(t)→0. 定理2 假设1满足.构造滑模面si(t)=ei(t).控制律为 不在滑模面上时,设计函数 由引理1得 由引理2,从而得到si→0⟹ei(t)→0. 以分数阶单摆混沌系统为例,使用Matlab工具箱中的软件程序进行数值仿真.令g=10,L=1,γ=0.46,q=0.86,Δf1(y,t)=cos(2πy2),Δf2(y,t)=0.5cos(2πy1).d1(t)=0.2cos(t),d2(t)=0.6sin(t). 定理2中设计滑模面si(t)=ei(t).控制律为 定理1与2自适应律设计为(i=1,2) 定理1误差如图3—4所示,定理2误差如图5—6所示.由图3—4中可看到,误差初始时刻相差较大,距原点较远,随时间推移,误差逐渐趋近于一致并向坐标原点趋近,表明系统取得同步.定理1与定理2的区别在于选取不同的滑模函数控制效果不同,定理1中设计的滑模函数和控制器都比定理2复杂一些,定理2中的滑模面简单实用,控制形式简单且控制效果良好.从图5—6上可看出定理1中误差摆幅较大,比较难于趋向稳定;定理2的误差摆幅则较定理1小一些,很容易趋近于原点,并趋于同步.文章设计了两种截然不同的滑模函数,当q=1时,分数阶系统退化为整数阶系统,该方法对整数阶系统仍然适用和成立. 图3 定理1第一误差 图4 定理1第二误差 图6 定理2第二误差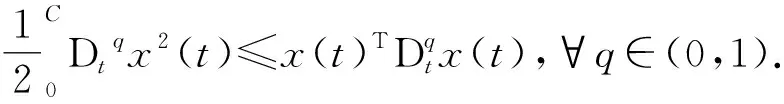
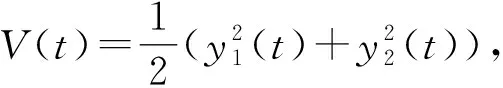
2 主要结果
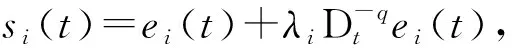
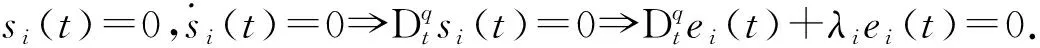
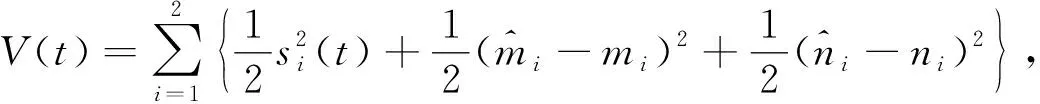
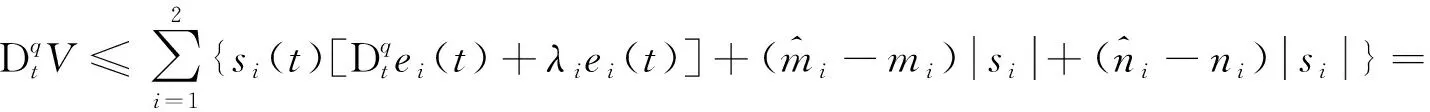
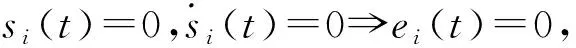
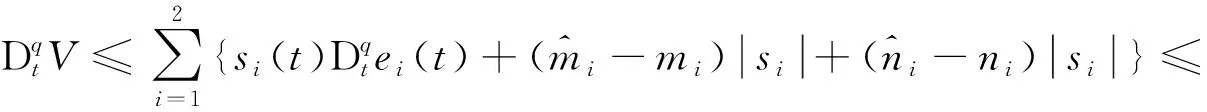
3 数值仿真