动态Casimir效应中的量子同步效应
2022-01-05关若男龙玉梅郑泰玉
关若男,龙玉梅,张 雪,郑泰玉
(东北师范大学物理学院,吉林 长春 130024)
真空扰动产生光子被人们称为动态Casimir效应(DCE)[1],这是量子电动力学最伟大的预言之一,1970年首次在理论上被提出.对动态Casimir效应的观测一直是许多科学家为之努力的一项工作,直到2011年Wilson等人利用超导量子干涉仪(SQUID)中断超导波导传输线,并通过对超导量子干涉仪(SQUID)的外部磁通量进行高频调制实现了动态Casimir效应的实验观测.实验表明,磁场诱导的有效运动产生了初始准真空状态下的微波光子对,这是人们第一次在实验中观测到超导电路中的动态Casimir效应[1-2].此外实验还证明DCE产生的光子对显示出了量子纠缠[3]和量子失谐[4].理论研究表明,即使在考虑环境热噪声的情况下,也可测量出量子关联,这使得我们可以对动态Casimir效应中的非经典特征进行量子化处理[3-5],这些关联可以被转换为超导量子位元,从而产生高度纠缠的量子位态[6].因此,更详细地研究如何利用DCE产生其他有用的量子关联以及它们在现实环境中对热噪声的鲁棒性,具有特别重要的意义.
近年来,两个或两个以上互连的经典系统的同步效应引起了广泛的关注.同步效应在许多领域表现出独特的应用潜力,例如互联网中信息的同步传输、耦合激光器之间信号的同步传输和放大、使用无序同步技术的信号的加密和解密等.人们开始期望在量子系统中发现类似的同步现象,以便实现量子信息或状态的同步传输.2013年,文献[7]将经典同步概念推广到量子系统,发展了量子系统演化的连续变量系统同步的定量理论.而且还介绍了量化耦合连续变量同步水平的两种不同措施.随后,在相关理论和实验方面取得了一定的进展,并得到了量子同步的判定标准.本文基于对超导电路中动态Casimir效应的研究,得出本文所选系统可以看作连续变量的高斯系统[8],根据Mari等提出的量子同步判定标准,进一步研究此系统的量子同步水平,以及系统中各因素对同步水平的影响.
1 理论模型
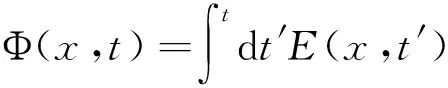
(1)
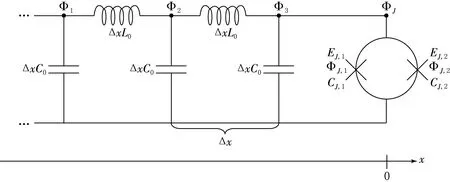
图1 一维半无限超导波导管理论模型示意图
根据文献[11-12],当超导量子干涉仪中的频率足够大时,超导量子干涉仪对磁通量场提供的边界条件为
Φ(0,t)+Leff(t)∂xΦ(x,t)|x=0=0.
(2)
定义有效长度为
Leff(t)=(Φ0/2π)2/(EJ(t)L0).
(3)
式中:L0为单位长度波导的特征电感;EJ(t)=EJ[Φext(t)]为与磁通量有关的有效约瑟夫森能,其中Φext(t)为超导量子干涉仪中的外加磁通量.对于谐波驱动频率ωd/2π与归一化振幅,可以得到sinωdt],则有效长度调制振幅为δLeff=Leff(0).若有效速度veff=δLeffωd相对于波导中的光速v来说很大,那么动态Casimir效应中发射的光子数非常多.
在这个框架下,利用散射理论研究动态Casimir效应,进一步讨论如何在含时边界条件中加入独立的输入、输出模式[13].在参考文献的微扰理论中[3,11-12]详细分析过,得到的输出场与模式中的角频率ω+,ω-有关,而ω++ω-=ωd,所以我们将ω+,ω-定义为ω±=ωd/2±δω,其中δω即为失谐.引入a±=a(ω±),b±=b(ω±)则输入、输出场的关系为
(4)
令
(5)
可以得到
(6)
2 应用于双模高斯态的量子同步理论
在海森堡绘景下,令q±,p±分别为系统两种模式对应的正则算符.由于平均值近似适用于介观系统,这就意味着介观系统中的算符o(t)可写为o(t)=〈o(t)+δo(t)〉的形式.因此可以将系统的误差算符写为:
(7)
(8)
其中:
其验证流程也十分简明,客户端使用用户凭据登录系统,服务器验证通过后,依据上述规则生成jwt 返回给客户端。客户端之后在向服务器请求时,通过header 中的Authorization 字段以Bearer 形式携带此token 来发送至服务器端验证身份和权限。一般的token流程可以由图2 来表示,申请为1~2 步骤进行,请求资源以3~6 步骤进行。
(9)
(10)
系统的量子效应可以由δo(t)来表征,所以在讨论因量子效应引起的同步误差时,只考虑δQ(t)与δP(t)即可,由于海森堡不确定性关系,二者都不能同时达到非常小的数值.出于这个原因,Mari等人,引入了基于方程(7)—(8)的品质因数为
(11)
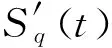
为了求解(11)式,这里引入协方差矩阵.对于任一连续变量的双模高斯系统,其协方差矩阵可表述为
(12)
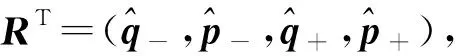
(13)
(14)
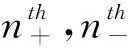
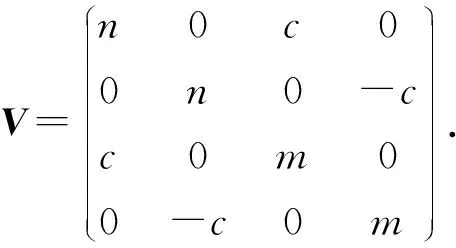
(15)
其中:
(16)
可由系统的主方程进一步推导出双模高斯态演化的协方差矩阵形式[15],i表示不同的通道.(15)式可看作描述此系统高斯态初始时刻的协方差矩阵,即
V(0)=V.
(17)
两个模式的演化矩阵可表述为
(18)
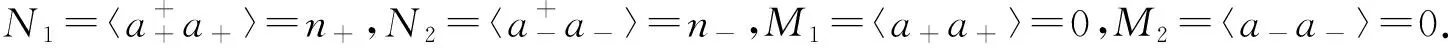
耦合后的耗散矩阵为
(19)
则系统状态随时间变化可由协方差矩阵描述[15]为
V(t)=V(0)e-γt+V∞(1-e-γt).
(20)
其中γ为耦合系数,这里讨论两个通道耦合系数相同的情况.将(17)和(19)式代入到(20)式得
(21)
其中:
得到了系统考虑耗散的双模高斯态协方差矩阵.将(21)式代入(11)式中,可得
(22)
3 影响系统同步水平因素的讨论
不同参数对系统达到同步时间的影响见图2.在图2(a)图中,v=1.2×108m/s,ωd=2π×10 GHz,k=1.38×10-23,δω/ωd=0.2,Leff(0)=0.5 mm,=0.5,γ=0.5,实线表示温度T=0.03 K,虚线表示温度T=0.05 K.在图2(b)中温度T=0.03 K,其他参量与图2(a)相同,实线表示=0.1,虚线表示=0.4.在图2(c)中实线表示δω/ωd=0.1,虚线表示δω/ωd=0.3,其他参数与图2(a)中一样.在图2(d)中实线表示γ=0.5,虚线表示γ=2,其他参数与前面一样.
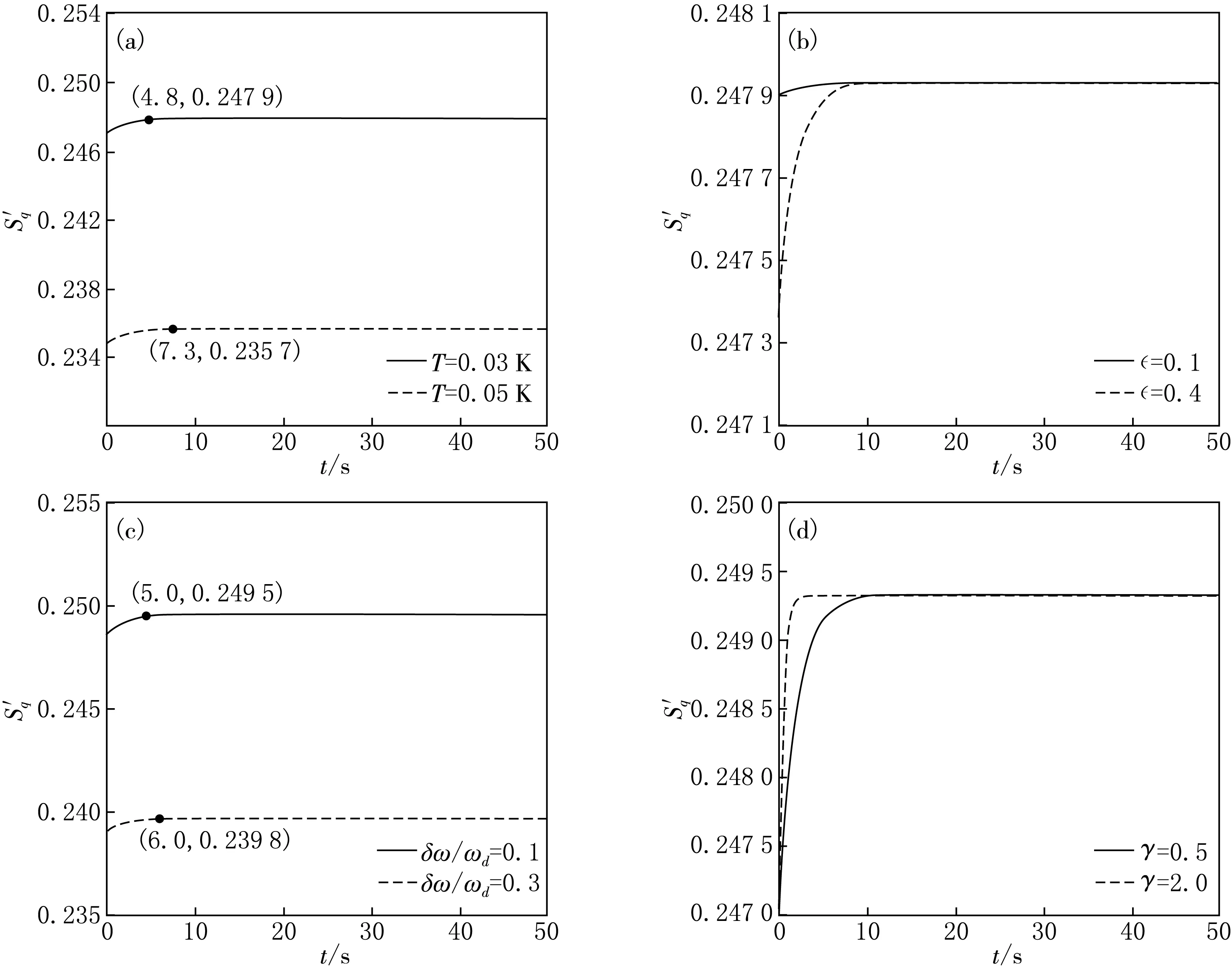
图2 不同参数对系统达到同步时间的影响
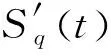
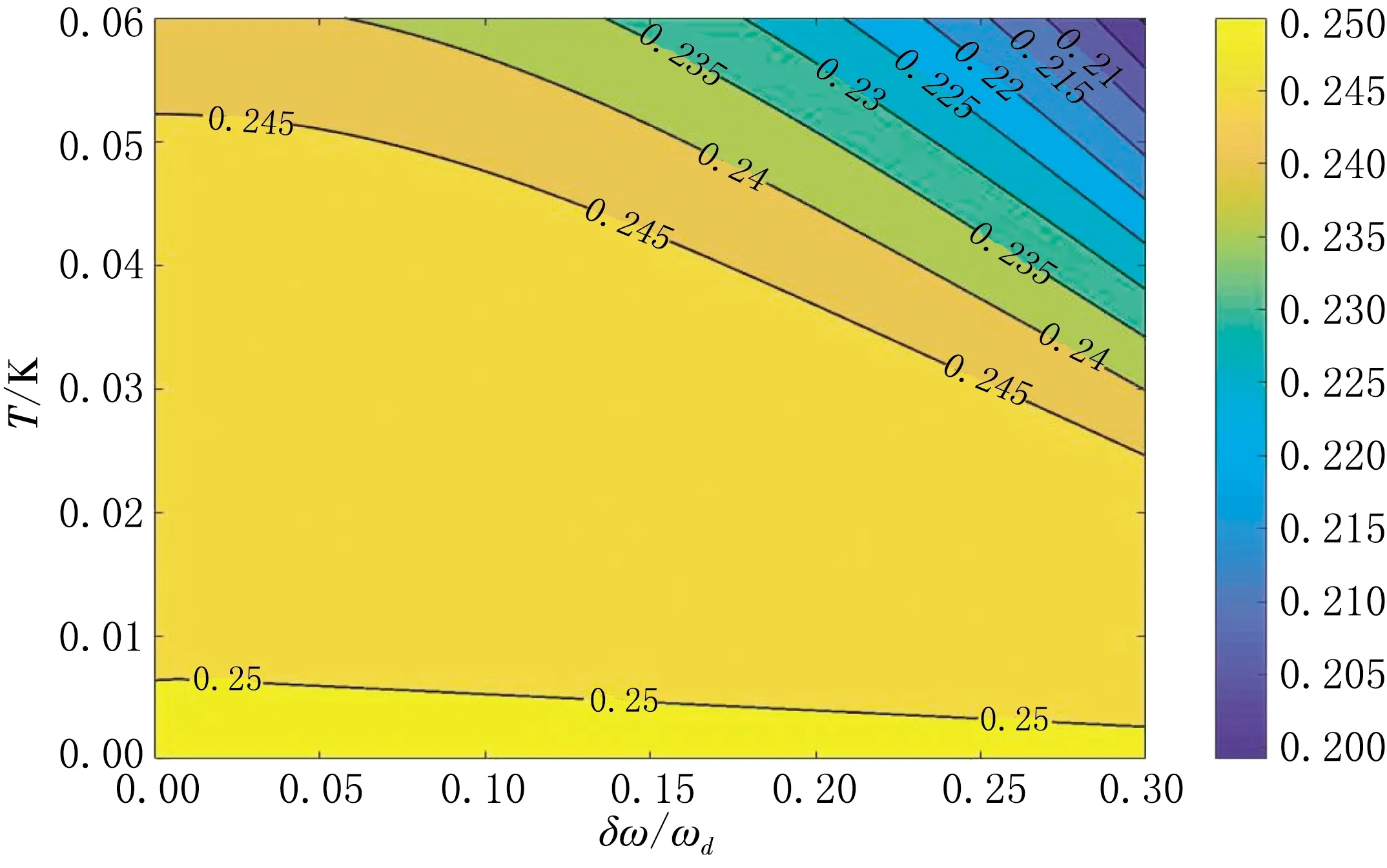
v=1.2×108m/s,ωd=2π×10 GHz,k=1.38×10-23,Leff(0)=0.5 mm,=0.5,γ=0.5
4 结论