考虑传感器倍频干扰的磁轴承自动平衡控制*
2022-01-05李延宝吕奇超周一恒
吉 文,李延宝,吕奇超,周一恒,陈 曦
(1.同济大学 磁浮交通工程技术研究中心·上海·201804;2.上海航天控制技术研究所·上海·201109;3.上海市空间智能控制技术重点实验室·上海·201109)
0 引 言
相对于传统的滚珠轴承,磁悬浮轴承利用电磁力实现了转子与定子的无接触支撑,具有无机械摩擦、无需润滑、参数可调等优点,被广泛应用于对精度要求高的超精加工、高速储能、航空航天等多个领域[1-2]。与其他旋转机械类似,磁悬浮转子也存在复杂的振动问题[3-4]。
实际测试数据表明,传感器倍频干扰是引发磁悬浮转子微振动的重要因素。特别是在特定转速范围内,传感器倍频信号分量与控制系统、结构模态相互影响,容易诱发共振,导致系统失稳[5-6]。
针对由传感器谐波噪声引发的倍频扰动问题,研究人员提出了多种辨识和抑制策略。Setiawan等[7]指出,传感器的感应面并非理想的圆形,其将在传感器信号中引入干扰,通过辨识轴承刚度的微小变化,可自适应确保转子几何中心的稳定。Xu等[8]提出了一种基于可变相位陷波反馈的同步电流抑制方法,该方法通过分析转子几何中心、惯性轴的同步位移关系,采用重复控制算法成功抑制了残余谐波振动。张激扬等[9]通过构造分级自适应相移陷波器,提高了系统在全转速范围内的稳定性。魏静波[10]结合磁悬浮转子位移传感器不对中的规律,基于低转速零同频位移控制设计了差值辨识方法,采用超前前馈补偿策略抑制了传感器的振动。Zhang等[11]进一步分析了由传感器跳动而产生的多谐振动的机理,采用将广义陷波器和重复控制相结合的方法,同时抑制了由转子质量不平衡和传感器跳动引起的谐波振动。张凯等[12]提出了一种同步坐标变换倍频谐波抑制策略,对磁悬浮鼓风机系统的三次谐波进行了筛选和滤除,取得了较好的效果。吕奇超等[13]指出,磁悬浮控制力矩陀螺内部的多源高频振动会导致系统出现谐波振动,进而提出了一种自适应跟踪滤波器,对系统同频和倍频分量进行辨识和抑制。任正义等[14]以600Wh飞轮储能系统为研究对象,采用数值积分法,经分析得知定转子在平动和倾斜运动过程中,改变飞轮转速或基础径向支承刚度会影响三个激励对应的频率分量和幅值。荣海等[15]通过引入多频率陷波器抑制了转子的同频与倍频振动,有效抑制了磁悬浮电主轴振动的动不平衡振动。
根据上述研究结论,不难看出,通过消除或抑制轴承的同频或倍频反作用力,可使由传感器谐波扰动产生的电磁力得到衰减。当磁轴承不产生与传感器谐波干扰信号同频的电磁力激励时,轴承基座也就不再产生相应的振动。为了研究大质量转子在更高转速下由传感器谐波噪声引起的振动问题,本文在以上研究的基础上,首先建立了考虑位移传感器倍频信号扰动的系统模型,分析了传感器谐波与系统微振动的内在机理,然后提出了一种基于自适应多频陷波器的磁轴承自动平衡控制方法,并通过仿真算例验证了该算法在抑制高速转子位移传感器谐波扰动方面的有效性。
1 系统结构与数学模型
本文研究了一种两自由度磁轴承,其结构示意图如图1所示。该系统主要由一个径向磁轴承组成,可实现转子的两个径向平动主动控制,而轴向平动控制和绕径向控制依靠磁轴承被动回复力实现。当磁轴承的线圈通过大小合适的电流时,铁芯内部将产生磁场,对转子形成一定的电磁吸力。电磁吸力将转子悬浮在空中,实现了定子与转子的无接触支撑。
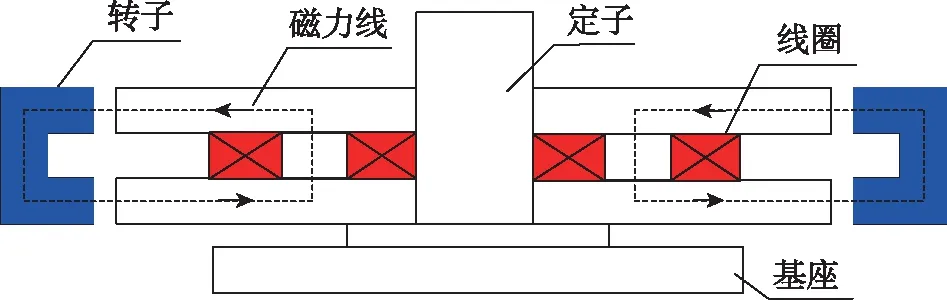
图1 两自由度磁轴承结构示意图
该磁轴承包含了4个位移传感器,如图2所示。4个传感器检测的转子位移信号分别为di(i=1,2,3,4)。两个轴承的几何中心轴线为Z轴。其中,传感器1、3为一组,两个位移的差构成了X轴的差动控制量;传感器2、4为一组,两个位移的差构成了Y轴的差动控制量。当差动控制量不为0时,控制系统将产生合适的电磁力,使转子的几何中心与Z轴重合。
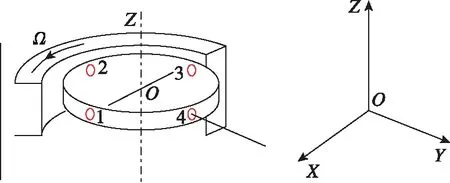
图2 两自由度磁轴承传感器布局
考虑到磁轴承X轴、Y轴方向的对称性,以上磁轴承以X通道为例开展研究。磁轴承的质心沿X轴的位移简记为x1,则有
x1=d1-d3
(1)
在平衡点附近,转子磁轴承沿X轴所受的电磁力为
(2)
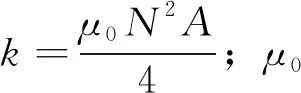
在平衡点处对电磁力公式进行线性化处理,得到电磁力fx1关于位移、电流的表达式当考虑传感器谐波扰动时,径向传感器的位移信号可表示为
fx1=kxx1+kii1
(3)
其中,kx是位移刚度系数;ki是电流刚度系数。
x1=x0+xs
(4)
其中,x0为转子X通道径向位移的基频分量。
一般地,位移传感器的谐波干扰xs可以表示为
(5)
其中,sk和φk分别为k次谐波干扰的幅值和初相位;ω为转子旋转角速度。
上磁轴承质心沿X轴方向的质心平移运动方程为
(6)
其中,m为转子质量。
将上述式子联立可得
(7)
由于两个平动通道X和Y的结构和控制方式相同,为了简化问题,这里可用一个单输入单输出系统来描述X通道的工作原理。图3所示为磁轴承X通道的闭环控制系统框图。其中,C(s)、Gi(s)、Gs(s)分别为控制器模块、电流环模块和传感器模块的传递函数。
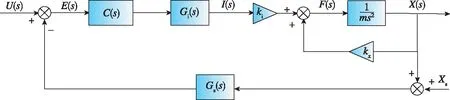
图3 单通道磁轴承闭环控制系统框图
根据图3,上磁轴承X通道的开环传递函数为
(8)
当考虑传感器的谐波扰动时,不妨以Xs(s)为输入,电磁力F(s)为输出,可得如下的传递函数为
(9)
由式(9)可知,位移传感器的谐波信号通过反馈进入控制系统,产生与谐波信号相关的微振动力。
2 考虑传感器倍频干扰的自动平衡控制器设计
针对由传感器谐波信号引起的倍频电磁力干扰,设计了一种抑制传感器倍频干扰的磁轴承自动平衡控制器。考虑传感器倍频干扰的磁轴承自动平衡控制框图如图4所示。
图4中,将考虑传感器倍频干扰的自动平衡控制器N(s)串入控制器C(s)的前端。其中,虚线框内的N(s)由多个级联的自适应同频信号陷波器组成,其传递函数可表示为[8-9]
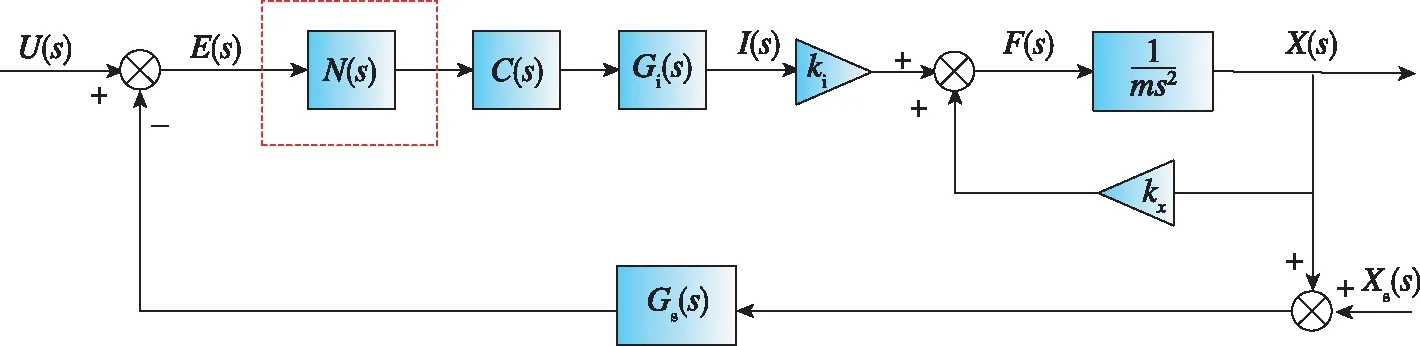
图4 考虑传感器谐波干扰的磁轴承控制系统框图
N(s)=N3(s)N5(s)N7(s)…N2k+1(s)
(10)
这里,k的取值为k≥1。这是因为,试验中发现的多为传感器奇数次谐波信号。
其中,Ni(s)的传递函数为[9-11]
(11)
这里,γ、p和q为可调参数。
引入自动平衡控制器后,以Xs(s)为输入,电磁力F(s)为输出,可得到系统新的闭环传递函数为
(12)
根据式(10)~式(11)可知,如果
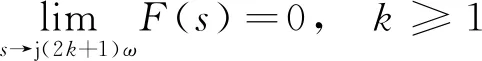
(13)
则式(12)表明,在理论上,此时该陷波器可以抑制由传感器倍频干扰引发的磁力振动。
3 仿真分析
高速磁悬浮转子的系统参数详见表1。位移传感器的干扰频率可分别设置为1500Hz、2500Hz。

表1 磁悬浮系统参数
结合上述系统参数,采用PID控制策略,当比例系数kP=3.8、微分系数kD=0.09、积分系数kI=0.11时,该系统可以实现稳定悬浮。当不采用传感器谐波扰动抑制措施时,在转速为30000r/min的条件下,系统的仿真曲线如图5所示。由图5(a)可知,由于位移传感器的倍频干扰,在30000r/min转速条件下,系统存在明显的、与转速500Hz同频、3倍频和5倍频的振动。图5(b)表明,当不采用主动振动控制时,由于位移传感器存在倍频干扰,电磁力将导致系统产生较大的振动,振动将达到120N。其中,与转速同频、3倍频和5倍频的振动力幅值分别为63N、41N和22N。不难看出,与转速同频的电磁干扰力最大。
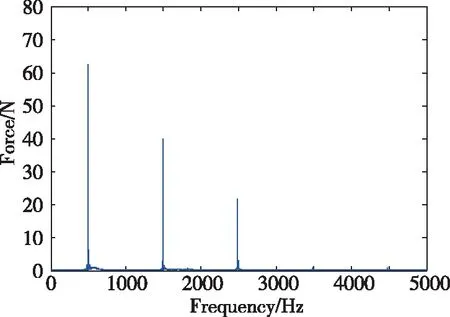
(a)不采用干扰抑制措施时的系统频域响应
当引入多个级联的自适应同频信号陷波器后,在转速为30000r/min时,令可调参数γ=0.45,p=80,q=-60,可得到图6所示的系统仿真曲线。
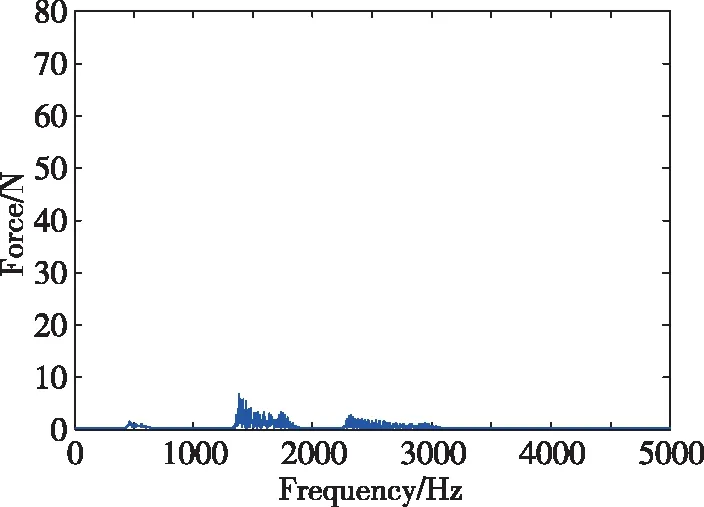
(a)采用干扰抑制措施时的系统频域响应
图6(a)表明,采用上述设计的位移传感器的谐波干扰抑制多频陷波器后,在30000r/min转速条件下,系统不再存在明显的与上述传感器倍频干扰相关的振动。由图5(b)可知,采取该主动振动控制措施时,电磁干扰力将减小到50N。其中,与转速同频、3倍频和5倍频的振动力得到了抑制,幅值分别衰减至约1N、6N和2N。不难看出,与转速同频的电磁干扰力仅为原来的1.6%。
4 结 论
针对磁轴承存在的位移传感器倍频干扰问题,本文重点研究了高转速条件下抑制位移传感器倍频干扰的有效方法。通过建立考虑位移传感器倍频信号扰动的磁轴承模型,得到了传感器谐波与系统微振动的内在机理,进而提出了一种基于自适应多频陷波器的磁轴承自动平衡控制方法。仿真结果表明,在转速为30000r/min时,采用上述自适应陷波器后,由位移传感器中与转速有关的同频、3倍频和5倍频等谐波干扰导致的电磁振动力得到了有效抑制。其中,与转速同频的电磁干扰力仅为原来的1.6%。
由于引入陷波器会增加闭环系统传递函数的阶次,有可能改变原系统的稳定性,后续将进一步研究增加陷波器后系统的闭环稳定性问题。
