多场景高分辨率遥感图像快速拼接技术*

吴 晗，金 磊

(北京航空航天大学 宇航学院·北京·102206)

0 引 言

光学遥感卫星的高分辨率和大视场是一对相互矛盾的指标，美国WorldView系列[1]、法国Pleiades系列[2]、印度Cartosat系列[3]、韩国Kompsat系列[4]，以及我国最新的高分系列卫星[5]，最高分辨率均能够达到1m，并且光学遥感卫星的空间分辨率也在向分米级、厘米级发展。但是，与此同时，光学有效载荷的视场范围也随之缩减。为了解决这一问题，工程领域已有多种解决方案，其中基于多相机、多视角的成像技术具有易于实现、有实时性、能够有效增加覆盖能力、可将高分辨率与大视场进行有效结合等优点，已在北京一号(BJ-1)卫星、资源一号02C(ZY-1 02C) 卫星、高分一号(GF-1)卫星、高分二号(GF-2)卫星以及法国SPOT-7卫星等卫星上得到了成功应用[6]。

自1996年Richard Szeliski总结并提出了基于图像间旋转、平移等多种变换技术的全景图像拼接经典模型[7]后，Burt、Brown和Lowe等也先后对该模型进行了改进[8-10]，并建立了遥感图像拼接的基本框架。图像配准是该框架中的关键步骤，包括角点检测与匹配两个部分。常用的角点检测算法有Harris[11]、尺度不变特征变换(Scale Invariant Feature Transform，SIFT)[12]、加速分割检测特征(Features from Accelerated Segment Test，FAST)[13]、加速鲁棒特征(Speeded Up Robust Features，SURF)[14]等。其中，SURF算法在效率和鲁棒性方面具备更多的优势，在图像拼接过程中得到了广泛应用。不同图像间的角点的匹配方法有序贯相似检测算法(Sequential Similarity Detection Algorthms，SSDA)[15-16]、层次性匹配方法[17]、KD树(K-Dimension Tree)算法[18]等。由于KD树算法具有较高的效率，其在特征点初始匹配阶段被应用得较多。在完成初始匹配后，利用随机抽样一致性(Random Sample Consensus，RANSAC)算法对匹配点对进行提纯、计算配准模型的单应矩阵是一种经典算法[19]。文献[20]根据配准得到的单应矩阵给出了一种相机参数估计方法，该方法有效降低了图像拼接的累积误差。

目前，遥感图像拼接算法的框架已经基本完善，如何提高拼接过程中的实时性以及对不同场景的适应性、鲁棒性等[21-22]是目前的研究热点。针对拼接过程实时性的研究主要包括两个方面：一是硬件加速的方法[23]，该方法能够极大程度地提高拼接效率，但过于依赖硬件，对成本的要求较高；二是改进拼接算法，该算法包括了对输入图像的预处理[24]和改进配准算法[25]等，能够提高配准的质量和效率，且不受成本限制，具有更高的研究和应用价值。但是，由于不同场景中的遥感图像所含信息的丰富程度不同，不同的算法对不同场景的图像具有不同的适应性和鲁棒性，进而可影响拼接的质量和成功率[26]。针对上述问题，本文对安装有多视角、高分辨率光学载荷的遥感卫星，提出了一种基于相机参数保持的快速拼接算法(改进算法)。相对于传统的拼接算法，该算法在配准前可将待拼接图像进行降分辨率处理。本文基于成像原理建立了相机内参矩阵的恢复模型，能够有效提高图像拼接的质量和效率，并研究了该算法对建筑、森林、湖泊、农田四种常见场景的适应性和鲁棒性。

1 图像拼接算法与流程

遥感图像传统拼接算法的流程如图1所示：首先，获取由多个光学成像系统拍摄的待拼接大幅面序列图像，对图像进行预处理，包括降噪、亮度校正和除雾；然后，对大幅面图像进行特征点检测与配准，获取相机参数，对遥感图像进行全局校正；最后，将遥感图像投影变换至对应模型，生成拼接区域，寻找待拼接图像的最佳缝合线，对缝合线进行膨胀运算，在缝合线两侧进行多分辨率融合。

图1 图像拼接流程

1.1 预处理

考虑到在卫星成像过程中，不同位置的光学载荷成像的亮度差异、图像噪声以及因云雾影响而导致的图像模糊，在获取遥感图像后，需首先对图像进行预处理，减少不必要的角点信息，提高图像质量及配准精度。

对不同位置光学载荷成像的亮度差异，可通过选择基准图像、利用RGB三通道直方图原理进行校正；对拍摄过程中遥感图像存在的噪声，可利用处理速度更快的高斯滤波算法对其进行去除；对因云、雾、气流引起的图像细节模糊，可采用基于暗通道的去雾处理方法[27]，其除雾模型为

I(z)=J(z)t(z)+A(1-t(z))

(1)

式中，I(z)表示待除雾的图像；J(z)表示无雾的图像；A表示全球大气光成分；t(z)表示折射率。

通过求取图像暗通道，在暗通道中计算得到全球大气光成分A、暗通道折射率t，根据式(1)即可计算除雾后的恢复图像

(2)

其中，t0为t(z)的下界，在本文中的取值为0.1。

1.2 配准与校正

(1)图像特征配准

对多幅遥感图像进行配准是进行图像校正、拼接和融合的基础。本文采用SURF算法对图像的角点信息进行了检测和描述，该算法对图像的尺度、光照、仿射变化具有一定的适应性和稳健性，且无论是从计算速度或鲁棒性角度考量，该算法均优于SIFT算法，其具体算法流程可参见文献[14]。

在得到遥感图像的特征点后，可采用基于KD树的最近邻搜索算法对图像特征点进行粗匹配，并运用RANSAC算法对误匹配点进行筛选。该算法通过反复迭代，可求解出一个符合最多样本数目的模型参数值，并确定单应矩阵H，最终将样本点分为内点和外点。内点为符合模型参数的样本点，反之为外点。

(3)

其中，h11、h12、h21、h22表示图像尺度和旋转量变换；h13表示水平方向位移，h23表示垂直方向位移；h31、h32表示水平和垂直方向的变形量。

(2)基于相机参数的全局校正

根据成像的几何基础，光学成像系统的参数包括内参矩阵M1和外参矩阵M2，如式(4)所示。设相机只做了旋转处理(或者认为物体离相机的距离很远)，则可通过RANSAC算法确定的单应矩阵H得到光学成像系统的内参矩阵，外参矩阵可由内参矩阵与单应矩阵求得

(4)

其中，u0、v0表示像平面坐标系中的坐标原点在图像坐标系中的位置；αx=f/dx，αy=f/dy，f表示成像平面到光心的距离，即焦距，dx、dy表示每个像素占据的物理长度，单位为mm；R、q分别表示世界坐标系到相机坐标系的旋转矩阵、平移向量。

由式(4)可得相机的估计参数，利用相机的估计参数可对待拼接的遥感图像进行校正。但是，估计参数与实际参数之间的误差会导致两变换图像间的重映射误差(如图2所示)。若待拼接图像的数量较多，拼接结果会出现明显变形，故可利用光束平差法(Bundle Adjustment)获取更精确的相机参数。

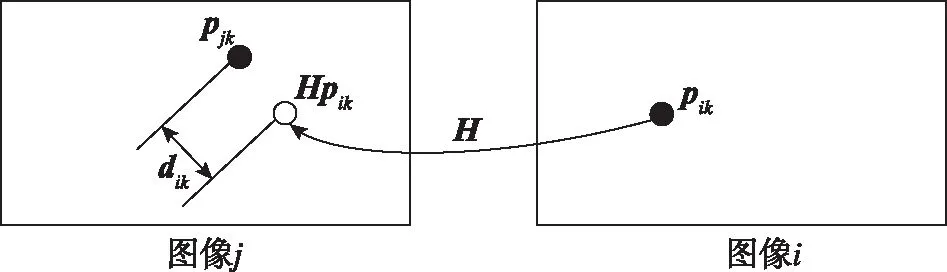
图2 图像重映射

定义Hpik点与匹配点pjk点间的距离误差为

dik=pjk-Hpik

(5)

对所有匹配特征点对的距离误差求和，可以得到待优化的目标方程

(6)

其中，n表示待拼接图像的数量；Γ(i)表示与图像i有匹配关系的图像的集合；F(i,j)表示图像i与图像j之间的匹配特征点的集合；h(·)为Huber鲁棒误差函数[10]。运用Levenberg-Marquardt算法迭代求解，优化单应矩阵H，使得目标方程(6)达到最小，即可获得精确的相机参数。

1.3 拼接与融合

由于光学载荷的位置不同，拍摄出的图像视角也不相同，因此在进行图像的拼接与融合之前，需要将待拼接图像投影生成拼接区域。常用的投影变换模型包括平面投影、球面投影、柱面投影和立方体投影[28]，为保证视觉效果，本文选用了平面投影。

为实现图像重叠区域的平滑过渡，避免出现拼接缝及重影，本文选用了基于最佳缝合线的多分辨率融合算法。最佳缝合线是指在两幅图像经过配准与变换后，在重叠区域内进行搜索并找到的一条两幅图像像素差异最小的线。本文选用动态规范法寻找最佳缝合线，其基本原理如下:

定义像素点(x,y)处的最佳缝合线计算准则

(7)

其中，Ecolor(x,y)为图像的颜色差异强度值；Egeometry(x,y)为图像的结构差异强度值[29]。

根据准则(7)，利用动态规划思想即可通过追溯而得到最佳缝合线：将重叠区域第1行的每个像素点作为起始点，计算每个点的准则值初始化为强度值；对每行的点向下一行相邻的3个像素点进行扩展，取强度值最小的点作为下一行的扩展点，并将该像素点更新为缝合线的当前点，直至最后一行；选择强度值之和最小的一组缝合线作为最佳缝合线。

针对拼接缝两侧的图像融合，本文采用了由Burt提出的多分辨率融合方法[8]。该方法对图像进行了高斯金字塔分解，然后建立了拉普拉斯金字塔，并基于拉普拉斯金字塔进行了图像融合，最后对合成图像进行了重构。该算法是一种低分辨率、多尺度的方法，能够获得更好的拼接效果，同时消除拼接缝。

2 遥感图像拼接系统的改进

图3 改进算法流程

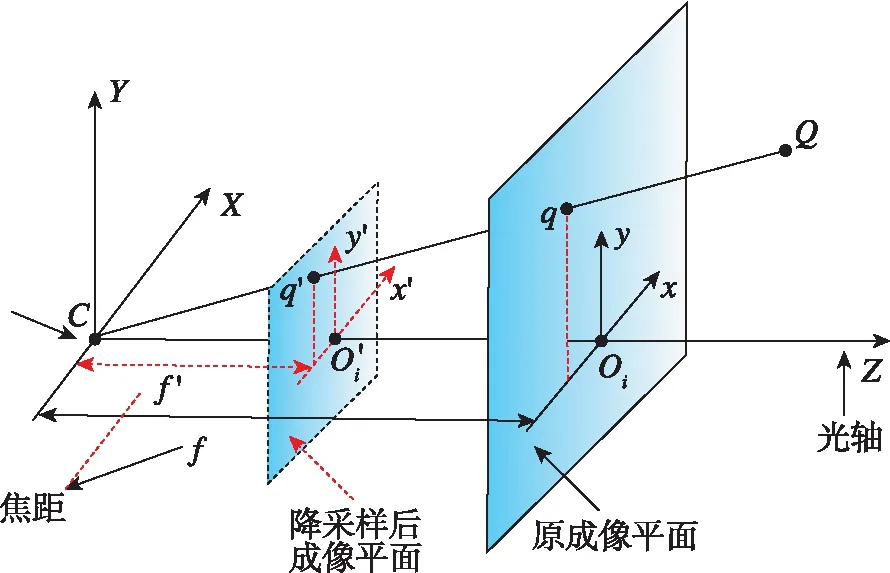
图4 相机成像原理

f=l×f′

(8)

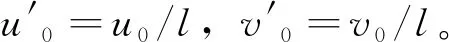
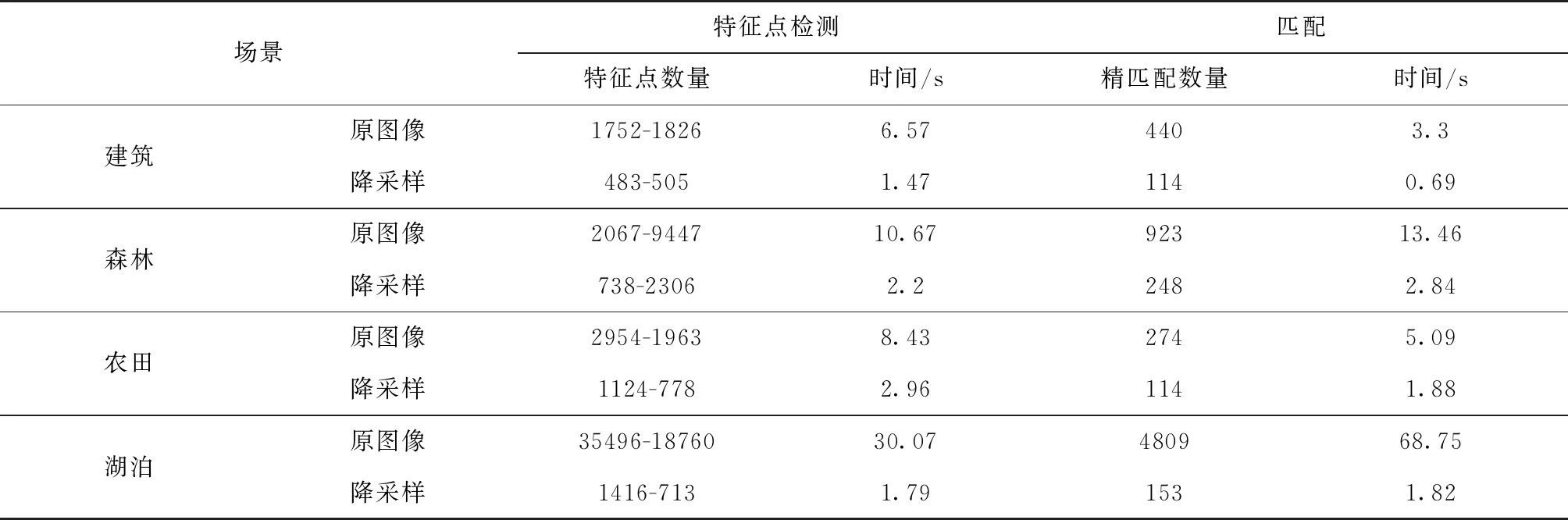
表1 特征点的检测与匹配过程

(a) 原图像

(9)

根据表1可知，对于建筑、森林、农田三种场景，特征点检测和匹配的数量能够降低约60%，同时检测与匹配的效率能够提高约60%；对于湖泊类场景，特征点检测和匹配的数量能够降低95%以上，而检测与匹配的效率能够提高95%以上。可以看出，本文提出的改进算法的本质是通过降低图像的分辨率，减少特征点的检测和匹配数量，提高配准和拼接的效率，这与理论分析的过程一致。

3 实验结果与分析

3.1 实验数据及环境

实验采用的测试图像为Inria Aerial Image Labeling Dataset遥感图像数据库。首先，将5000像素×5000像素的图像裁剪为2000像素×2000像素的图像，确保相邻图像间具有25%的重合度；然后，再将裁剪后的图像进行透视变换，以模拟相机间不同的位置。

遥感图像拼接系统由C++编程语言实现。其中，图像的拼接处理调用了OpenCV开源代码库，实验的硬件配置为Inter(R) Core(TM) i5-5200CPU@2.2GHz，RAM为4.00Gbit的PC，采用的集成开发环境是Windows10(64位)操作系统下的Microsoft Visual Studio2012。

3.2 评价指标

在完成遥感图像的拼接后，对拼接图像的质量进行评价是重要的一环。目前，常见的评价方法可分为两种：一类是主观评价，即通过人眼的视觉效果对拼接图像进行定性评价，该方法受主观因素影响较大；另一类是客观评价，即通过建立拼接图像与待拼接图像或拼接图像与参考图像间的数学关系，进行定量计算，对计算结果进行判断。本文选用交叉熵作为客观评价标准。交叉熵能够反映图像信息的数量，是评价图像质量的重要指标。交叉熵越小，表明两幅图像拼接效果越好。图像P与图像Q之间的交叉熵可定义为

(10)

式中，P={p(0),p(1),…,p(i),…,p(L-1)}、Q={q(0),q(1),…,q(i),…，q(L-1)}分别表示两幅待拼接图像的像素值分布；L表示图像的灰度级。

若拼接系统存在参考图像，则将式(10)的P、Q分别用拼接图像与参考图像进行替换即可。但是，大多数拼接系统均不存在参考图像。设F表示拼接完成的图像，定义拼接前的图像P、Q与拼接图像F的交叉熵CEN(P∶F)和CEN(Q∶F)，然后通过求取均值，可得到总体交叉熵，用于进行图像的客观评价

(11)

3.3 实验结果

(1)改进算法的效率与参数恢复精度分析

本文设计的算法通过改进配准过程提高了拼接的效率。为进一步说明本文算法的优势，有必要对降分辨率前后相机参数的恢复精度以及配准时间进行研究。对原图像进行降2下采样，即通过下采样将分辨率为2000像素×2000像素的图像降至1000像素×1000像素，然后统计配准时间，求解降分辨率前后相机参数间的误差。在4个典型场景的图像库中，各选取一组(上下左右共四张)待拼接图像进行测试，得到的降分辨率前后的配准时间对比如表2所示，相机参数误差如表3所示。

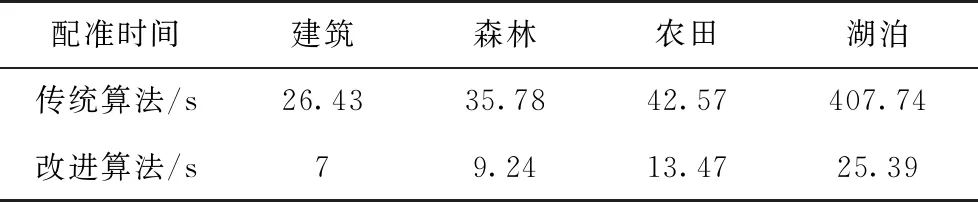
表2 降分辨率图像与原图像的配准时间对比

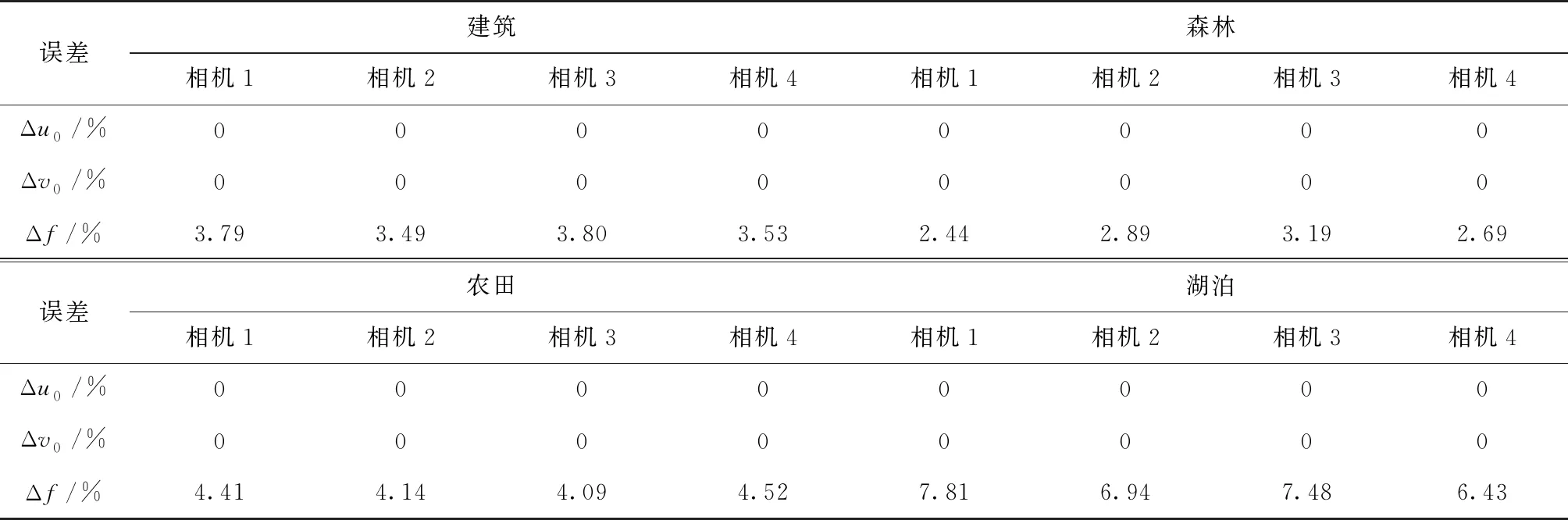
表3 降分辨率前后的相机参数误差

由表2可知，该算法能够将遥感图像配准时间缩短至不到之前的50%,特别地，湖泊类遥感图像的配准时间缩短至此前的30%，这表明该算法的加速效果显著；由表3可知，改进算法获得的相机内参能够恢复至与原图像坐标一致，而焦距f的恢复误差在8%以内。因此，该算法在保证拼接速度的同时，能够恢复相机参数，保证拼接质量。

(2)四类典型场景拼接质量分析效果评价

针对建筑、森林、农田、湖泊四种不同场景的遥感图像，在每种场景中进行5组实验。以原拼接算法作为对比，对本文提出的改进算法进行验证，选用主观评价与客观评价相结合的方式对遥感图像拼接结果进行综合评价。

事实上，两种算法对四种场景中的遥感图像均可实现高质量的拼接。除在农田、建筑两类场景中，个别拼接结果的细节方面存在细微差别(如图6所示)，其他场景和拼接结果的差异几乎很难通过肉眼观察到。图6(a)展示了改进算法在图像拼接细节处的优势，图6(b)展示了传统算法在图像拼接细节处的优势。因此，仅通过主观评价无法确定两类算法的优劣，还需要借助客观的评价指标。

(a)第一组

根据式(10)～式(11)计算拼接图像与待拼接图像的交叉熵、拼接图像与参考图像的交叉熵。在完成统计后，对各场景得到的实验数据求取均值。表4给出了四种场景中图像拼接效果的客观评价指标。由表4可知，相对于传统算法，本文设计的改进算法能够将拼接图像的拼接质量提升5%～35%。其中，算法对农田场景的图像质量的提升效果最为明显，建筑和湖泊场景次之，对森林场景的图像质量提升效果最小。综合主观评价，改进算法能够最大程度地保留原图像的信息。

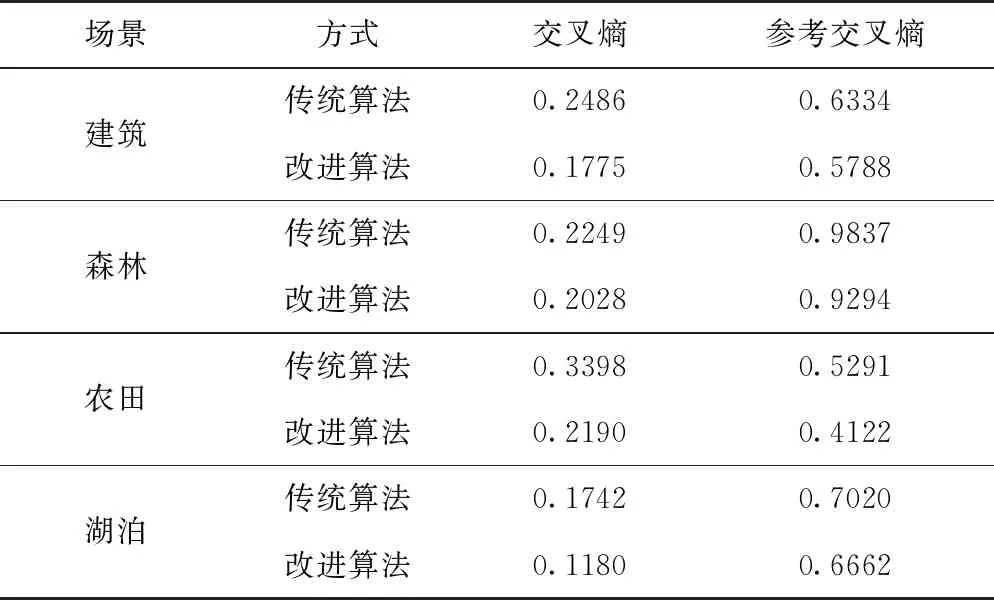
表4 不同场景拼接效果客观评价

(3)鲁棒性测试

以上实验过程均采用了理想情况下的遥感图像，没有考虑在成像过程中由常见的噪声、亮度差异、相机运动或抖动而引起的模糊等问题。在遥感图像的实际拼接系统中，这些问题会影响角点配准的准确性，从而导致图像质量降低甚至拼接失败。因此，有必要对改进算法的有效性和鲁棒性进行测试。本文采用在1.1节中介绍的方法对不同环境下的遥感图像进行了预处理，图7展示了不同环境下遥感图像的拼接结果。

(a)亮度差异明显

根据图7可知，无论对于存在亮度差异、模糊，还是存在噪声的遥感图像，该系统均能够较好地消除图像噪声、亮度跳变、拼接缝和重影等问题，这说明该系统具有可行性，对于由环境或相机参数而引发的图像质量降低具有鲁棒性。

4 结 论

本文针对安装有多视角光学载荷的卫星，研究了多场景高分辨率遥感图像的快速拼接技术，并提出了一种基于相机参数保持的快速拼接算法。该方法通过检测降采样图像的角点信息，利用降采样图像的配准信息恢复了原相机的参数，最后进行了图像的变换与融合，得到了高分辨率、大幅面的遥感图像。对建筑、森林、农田、湖泊四种场景进行了拼接实验。实验结果表明，该算法对遥感图像的亮度差异、模糊程度变化及图像噪声具有较好的鲁棒性。相对于传统算法，该算法能够恢复原相机的参数，将配准时间缩短至不到此前的50%，且能够将拼接图像的质量提升5%～35%。