运载火箭十表捷联惯组配置的故障诊断与决策*

李桂芳，王 威，王 鹏

(1.上海交通大学 电子信息与电气工程学院·上海·200240；2.上海航天控制技术研究所·上海·201109)

0 引 言

近年来，随着现代控制理论、计算机技术和航天技术的发展，运载火箭对导航制导系统的可靠性和精度提出了更高的要求。捷联惯导系统以其低成本和便于维护等优点，在导航领域发挥着越来越重要的作用。捷联式惯导系统(Strap-down Inertial Navigation System， SINS)在平台式惯导系统的基础上发展而来，是把陀螺仪和加速度计等惯性仪表直接固联在载体上，用计算机完成导航电子平台功能的惯性导航系统[1]。相对于平台惯性组合，捷联惯导组合在质量、体积、价格等方面均具备一定的优势，因而在航空航天领域得到了广泛的应用。

故障诊断的主要方法有基于硬件冗余[2-3]、基于解析技术[4-6]、基于知识[7]、基于信号处理[8]等的诊断方法。运载火箭固有的特点要求故障诊断系统能够快速准确地检测出故障数据，并进行迅速的判断、处理，以确保顺利完成飞行任务。为了提高导航系统的精度和可靠性，目前国内外在研、在役的运载火箭大多采用冗余技术消除I、II类单点数量，同时通过引入容错技术和故障诊断技术以提高系统的可靠性。其中，器件级冗余技术通过单纯地增加器件的数量即可大幅提升系统的可靠性，因而在提高可靠性和控制成本等方面，其较系统级的冗余技术具有较大的优势[9]。

由于惯性器件是惯组中的关键部件，因此，冗余配置的捷联惯导系统主要针对惯性器件进行故障检测和诊断，使系统具备应对一定程度故障的容错能力，进而可提高整个导航系统的可靠性。系统惯性器件的配置数目和结构、故障诊断方法、故障检测门限的设计都将影响系统精度及可靠性[10]。

单套“十表”配置的惯组由5个陀螺和5个加速度计组成，单表配置的捷联惯导系统在可靠性、经济性和简易性等方面均体现出了一定的优势，将成为后续型号应用的主流[11]。本文提出了一种针对“十表”配置的捷联惯组故障诊断算法、诊断流程、信息重构方案及故障诊断门限设计方法。

1 “十表”捷联惯组及其决策流程

1.1 “十表”捷联惯组配置方案

本文研究的“十表”捷联惯组配置了5个陀螺仪和5个石英加速度计，其中采用了3个陀螺仪(加速度计)正交安装、另外2个陀螺仪(加速度计)斜置安装的配置方案。箭载计算机通过采集陀螺仪和加速度计的输出[9]，即箭体坐标系的角速度和视加速度信息，进行导航、制导及姿态方程的计算，其示意图如图1所示。

图1 “十表”捷联惯组冗余配置示意图

图1中，Gx、Gy、Gz、Gs、Gt为5个光纤陀螺,其中，Gx、Gy、Gz为正交安置，测量轴正向为箭头所指方向；Gs、Gt为斜置安装，分别沿OS、OT轴安装，测量轴正向为图中箭头所指方向。Ax、Ay、Az、As、At为5个石英挠性摆式加速度计，其中，Ax、Ay、Az为正交安置，测量轴正向为箭头所指方向；As、At为斜置安装，分别沿OS、OT轴安装，测量轴正向为图中箭头所指方向。X1、Y1、Z1为箭体坐标系，Xs、Ys、Zs为惯组坐标系，Z与X、Y遵从右手定则。

其几何配置矩阵为

(1)

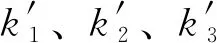
m=Rω

(2)

根据式(2)，采用最小二乘法可以得到

ω=(RTR)-1RTm

(3)

矩阵R含有5行，当5个陀螺中有1个出现故障时，有

mi=Riωi=x,y,z,s,t

(4)

式中，mi表示除去第i个陀螺故障的测量值后的测量向量;Ri为对应的测量矩阵。此时，tr(Ri)=3，可得到

(5)

理论上，根据矢量分配关系，几何配置矩阵R的任意3行组成的矩阵均满秩。惯组中，5个陀螺表头中的任意4个表均满足一定的数学关系，输出具有一致性，即任意1个表的输出可以用其余4个表中的3个表的输出来表示。如在正装表没有故障情况下，有

ms=k1mx+k2my+k3mz

(6)

(7)

1.2 冗余决策流程

在n维空间中，至少(n+1)个传感器的配置才能检测故障，至少(n+k+1)个传感器的配置才能检测并隔离k度(陀螺、加速度计分别计算)故障。“十表”捷联惯组陀螺和加速度计分别配置了5个表头。在正常状态下，任意3个表头即可构建导航系统，可以实现“十表”捷联惯组陀螺和加速度计分别存在1度故障的隔离与重构。

从系统的角度，根据“十表”捷联惯组输出脉冲，进行故障诊断算法及故障门限设计。通过故障判别和表决，输出各个表头的结果，进而计算火箭的姿态角、速度、位置等导航信息[11]，实现火箭的正常飞行。

根据表决结果，在正装表正常时，仅需采用3个正装表参与解算。若正装表被诊断出异常，再引入其他表参与解算。即在进行表头可用状态判别之后，如果X、Y、Z表头信息可用，则采用正装表信息；如果正装表有异常，根据十表“三正两斜”的配置结构。当X表或Y表出现异常时，采用Z、S、T三个表头参与解算;当Z表出现异常时，采用Y、S、T三个表头参与解算。

在故障判别和表决过程中，对敏感器的角速度和视加速度信息，常采用常零判别和一致性判别方法，同时也需要设计合理的故障门限。门限值过大，容易产生漏检；门限值过小，容易产生误检，进而将直接影响系统的误检率和漏检率。

“十表”捷联惯组的单表冗余决策流程如图2所示。

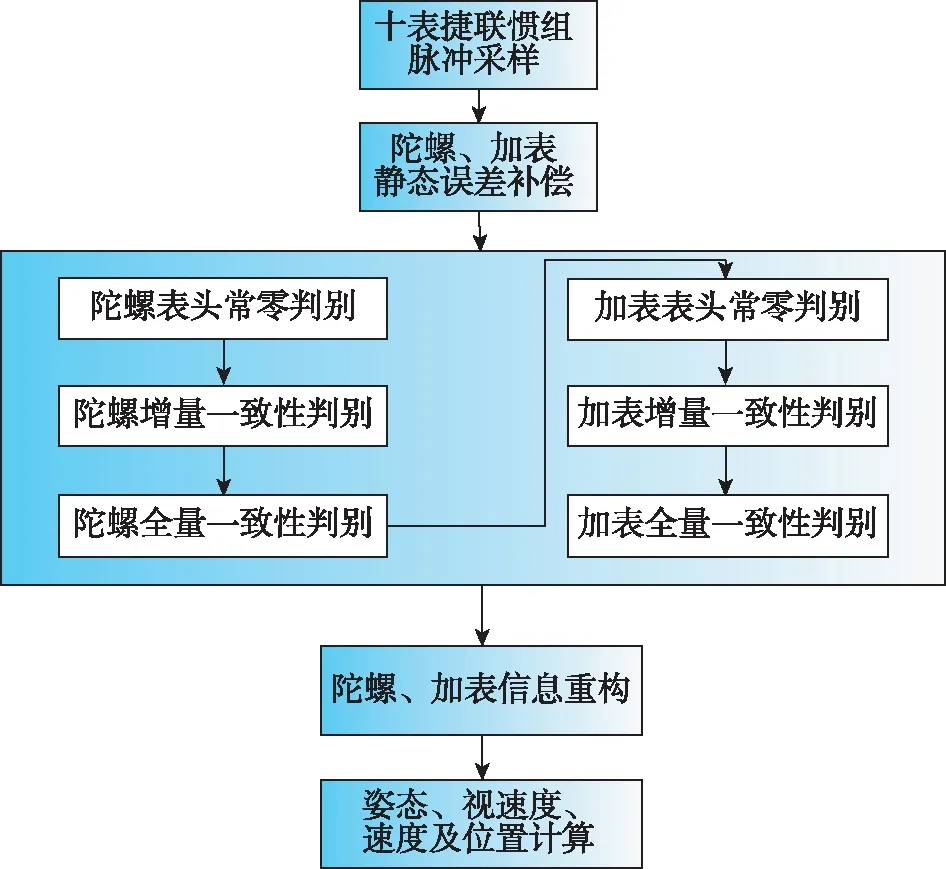
图2 “十表”捷联惯组冗余决策流程

2 故障诊断算法与信息重构方案

2.1 故障诊断算法

在单表惯性导航系统的故障诊断中，采用常零判定、一致性判定对系统故障进行检验。

2.1.1 常零判别

常零故障是指捷联惯组所有陀螺和加速度计的输出均值近似为零，陀螺和加速度计的输出绝对值小于一定门限则被判别为常零故障[12]。由于“十表”捷联惯组为单表冗余，常零故障判别需针对单个表头进行。采用原始增量脉冲进行运算，判别方法如下

(8)

(9)

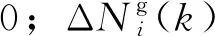
该诊断方案在全程范围内进行常零判别。当表头的常零故障计数达到故障门限后，故障表头暂时不参与导航解算，采用其他表头进行解算；若后续判别出该表头不是常零输出，则可继续参与导航解算，重新进行常零故障计数。

2.1.2 增量一致性判别

一致性判别的原理是将正装表的输出值向斜轴方向投影，投影值之和与斜装表测量值的差值构成了残差函数。通过对残差值进行门限判别，进而确定是否发生了一致性故障。若残差绝对值较大，则认为发生了一致性故障；否则，认为无故障。一致性判定的数据采用静态误差补偿后的惯组角增量或视速度增量数据进行累加，得到Nsnum拍的角增量累加和以及视速度增量累加和，分别按下式进行一致性判别[13]

θbs-k1Gθbx-k2Gθby-k3Gθbz≤δGself

(10)

Wbs-k1AWbx-k2AWby-k3AWbz≤δAself

(11)

式中，θbs、θbx、θby、θbz分别为惯组Nsnum拍输出值的角增量累加和;Wbs、Wbx、Wby、Wbz分别为惯组Nsnum拍输出值的视速度增量累加和;k1G、k2G、k3G分别为陀螺X、Y、Z轴向S轴的投影系数(常值);k1A、k2A、k3A分别为加速度计X、Y、Z轴向S轴的投影系数(常值);δGself、δAself分别为陀螺和加速度计的一致性门限，可通过误差模型计算得出。

在n维空间中，(n+1)个传感器的配置只能检测故障而不能分离故障。仅对5个表头(X、Y、Z、S、T表)中的4表的输出进行一致性判别，不能达到分离故障的功能。因此，需要对5个表头中的任意4表进行一致性判别，共计5组。当只有其中1组满足一致性时，系统才能分离出表头故障，分离各表头故障需满足的条件如表1所示。

表1 分离表头故障需满足的条件

单十表冗余状态可以通过故障诊断实现1度故障的隔离，但不能实现2个表头(陀螺、加速度计分别考虑)同时的故障检测及隔离。

在进行一致性判别时，设定S轴为主斜轴，采用如下配置进行载体系角增量Δθb及视速度增量ΔWb计算：

用由XYZ陀螺计算所得的Δθb用于XYZS和XYZT陀螺的一致性判别，将由XYT陀螺计算所得的Δθb用于XYST陀螺的一致性判别，将由YZT陀螺计算所得的Δθb用于YZST陀螺的一致性判别，将由XZT陀螺计算所得的Δθb用于XZST陀螺的一致性判别。

用由XYZ加速度计计算所得的ΔWb用于XYZS和XYZT加速度计的一致性判别，用由XYT加速度计计算所得的ΔWb用于XYST加速度计的一致性判别，用由YZT加速度计计算所得的ΔWb用于YZST加速度计的一致性判别，用由XZT加速度计计算所得的ΔWb用于XZST加速度计的一致性判别。

2.1.3 全量一致性判别

增量一致性判别常用于诊断惯性仪表突发性快速发散的故障，但对表头慢漂故障不能进行有效的识别。为了解决这个问题，采用长时间的故障累加进行故障判别。全量一致性判别的原理与增量判别类似，通过构造残差函数，间隔一定的周期，采用角增量、视速度增量进行累加，然后进行故障判别。需要说明的是，为了防止误判，视速度全量一致性判别门限需要结合相应弹道的过载特性进行设计。

为了防止故障信号反复引入系统，在判出不一致后，需进行故障计数。累计达到门限后，可将故障表头切掉，不再参与导航解算。

2.2 信息重构方案

在对5个表头进行一致性故障判别后，还要结合表头常零故障的判别结果，确定可用的表头。在确定可用的表头时，如果可用的表头的数量小于3个，则降低常零判别结果的参考性，将通过常零判别出不可用的表头的状态升级为可用，然后再采用无故障的表头信息进行捷联解算。信息重构方案的表头可用状态的判别算法如下:

(1)陀螺判别

Use_Gi=!(K0_GiorKself_Gi)i=x,y,z,s,t

(12)

其中，K0_Gi=1表示陀螺表头常零故障；Kself_Gi=1表示通过增量或者全量一致性判别后,判出表头故障；Use_Gi为1时，陀螺表头可用，为0时，表头不可用。

如果∑Use_Gi<3，则Use_Gi=!(Kself_Gi),

i=x,y,z,s,t。

(2)加速度计判别

Use_Ai=!(K0_AiorKself_Ai)i=x,y,z,s,t

(13)

其中，K0_Ai=1表示加速度计表头常零故障；Kself_Ai=1表示通过增量或者全量一致性判别后，判出表头故障；Use_Ai为1时，加速度计表头可用，为0时，表头不可用。

如果∑Use_Ai<3，则Use_Ai=!(Kself_Ai),

i=x,y,z,s,t。

在十表惯组“三正两斜”配置构型中，信息重构策略需考虑斜表的投影影响。如果陀螺或加速度计可用的表头数为5，则采用3个正装表参与解算；如果可用的表头数为4，则当X表或Y表有异常时，需采用ZST表参与解算,当Z表有异常时，需采用YST表参与解算，否则采用3个正装表参与解算；如果可用表头数为3，则采用3个可用的表头进行解算。在不一致性判别结果为4个表头的情况下，故障诊断及信息重构的关系详见表2所示。

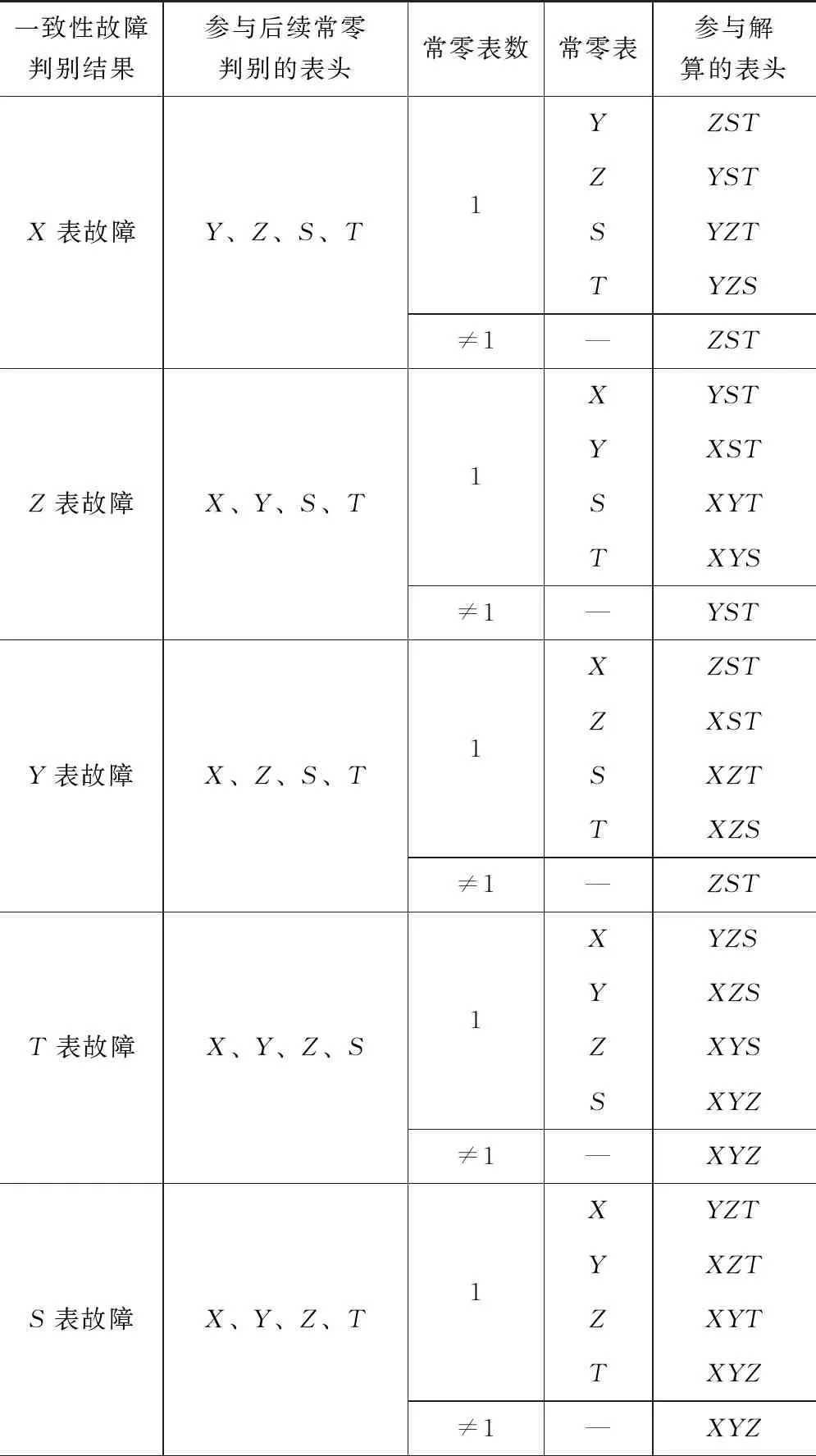
表2 故障诊断及信息重构关系

2.3 累加和替换及重调处理

根据一致性判别，能够将故障定位到具体表头，因此可对故障表头进行处理，使当前拍的故障信号不会污染到后续增量累加和处理，进而不会影响故障判别。对采用故障表头计算的用于一致性判别的角增量或视速度增量进行重调或替换，为获取正确的增量累加信息，可采用参与导航的三表静态误差的补偿结果进行重调。

在表头发生故障而未到一致性门限前，故障信息会进入系统，影响导航解算。即使单十表系统采用先控后切的模式，仍然会有部分故障信号被引入，对系统产生影响。

姿态误差需要用无故障陀螺解算姿态重调当前的姿态解算结果，如果以3个陀螺为一组进行热备份姿态解算，每一组陀螺可隔离2个陀螺故障。由于5表中任意1表均有可能发生故障，在考虑1度故障的情况下，则最少需要选择三组陀螺才能够保证在发生故障时有一组陀螺的备份姿态解算结果正确。

就独立性而言，在x、y、z、s、t陀螺中选取三组陀螺。由于X、Y、Z轴相互垂直，独立性最好，故为第一组陀螺选取X、Y、Z三轴。根据十表光纤惯组中陀螺的投影系数，在S轴投影系数中，z陀螺的系数最小。在T轴投影系数中，同样是z陀螺的系数最小，故选出第二组Z、S、T。在第三组陀螺中，不能包括Z轴，可选X、Y、S。在研判出各轴的故障后，采用的姿态重调的组合如表3所示。

表3 故障表头与姿态重调组合

3 故障门限设计

在故障诊断中对残差的假设检验，通常是将残差值与故障门限值进行比较。因此，门限值的合理设计是故障检测的关键，它是判别该系统是否发生故障的标准[14]。十表故障诊断的门限设计主要包括常零判别门限、增量一致性门限、全量一致性门限。门限设计要充分考虑飞行弹道的特点、惯性器件的特点以及对入轨精度的影响[15]。主要可从以下几个方面分别进行考虑：

(1)常零判别在全程范围内进行，出现误判的概率较大；若表头在火箭大机动飞行段出现常零故障，系统会进入增量或全量不一致区域；十表惯组的常零判别不作为表头故障判别的依据，而仅作为该表是否参与导航解算判断的依据。因此，当十表惯组表头在采样周期内的输出为0时，需累计一定时间才可判定该表头为零输出。

(2)增量一致性门限设计，可根据惯组陀螺、加速度计输出误差模型，最大角速度、视加速度需考虑恶劣情况，并取一定余量进行计算

δωb=Eg-1δEgω+Eg-1δD0+δGω+Eg-1δGD0

(14)

δa=εa-1δεaa+εa-1δK0+aδa+εa-1δaK0

(15)

式中，δωb、δa分别为陀螺输出误差角速率、加速度计输出误差视速度；Eg、εa分别为陀螺、加速度计安装系数矩阵；δEg、δεa分别为陀螺、加速度计安装误差矩阵；ω为角速率向量；a为视速度向量；D0、K0分别为陀螺、加速度计零偏；δD0、δK0分别为陀螺、加速度计零偏稳定性；δG、δa分别为陀螺、加速度计标度因数重复性。

(3)十表捷联惯组全量一致性判别旨在剔除增量一致性判别检测不出的慢漂故障，考虑到微小故障本身对系统的影响较小，可从误检角度对全量一致性门限进行设计。

4 仿真验证

故障诊断仿真通过在表头加入故障信息，比较表头输出的一致性曲线及故障表头信息，从而验证该故障诊断及重构方法的有效性及正确性。以十表惯组作为备份的某一发任务飞行试验数据为例，在10路遥测脉冲输出上模拟了各表头的故障输出。由于正常状态仅采用正装表信息进行计算，为了便于比较，这里仅模拟正装陀螺表故障的情况。

在每个采样周期中，将X陀螺表头多注入1个脉冲故障，陀螺输出的增量一致性曲线如图3所示，陀螺输出的全量一致性曲线如图 4所示。可以看到在0.3s后，XYZS/XYZT/XYST/XZST超出了设计门限，而YZST在设计门限内。根据方案及设计门限，系统将在2.8s判别出X陀螺的表头故障。

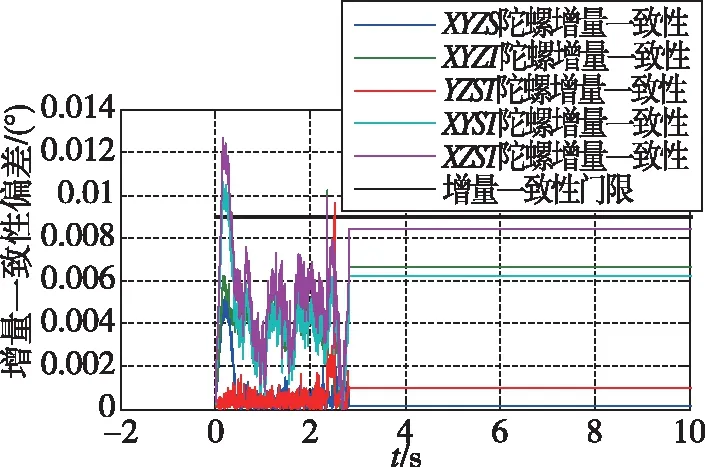
图3 陀螺输出的增量一致性偏差

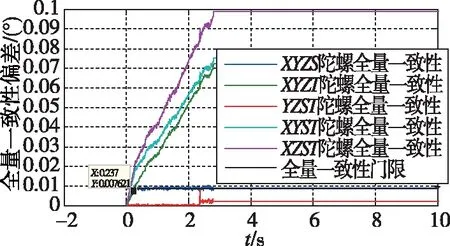
图4 陀螺输出的全量一致性偏差

根据该重构方案，系统计算姿态采用的表头信息如图5所示。其中，1表示在用，0表示没有使用。在判出X故障后，系统采用正确的ZST陀螺表头信息进行姿态解算。在Y、Z陀螺表头加入故障后，系统均能根据故障诊断与决策方案快速判别出故障表头，并采用正确的表头进行捷联解算。最终的导航结果对比如表4所示。

图5 导航系统采用的表头

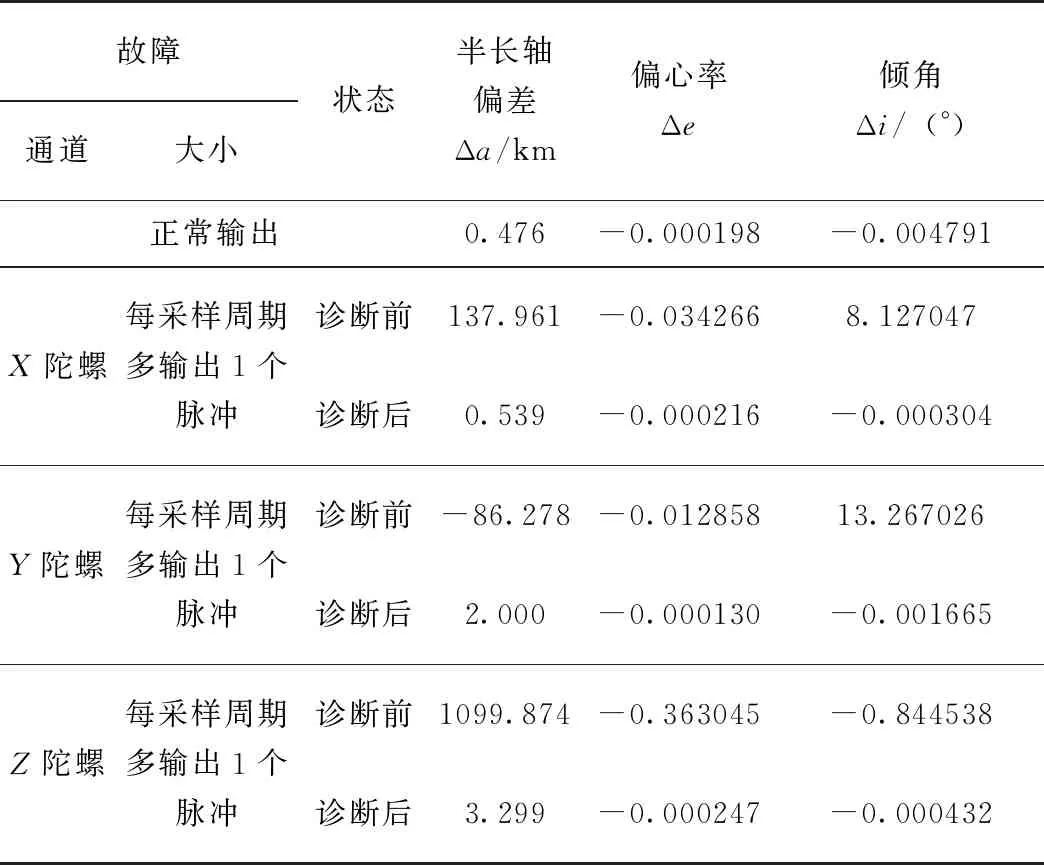
表4 导航结果比较

由上述仿真结果可知，当惯组的某个表头发生故障却不进行故障诊断与决策时，入轨精度的各项指标均严重超差，控制系统将无法完成飞行任务；经执行本文所提出的故障诊断与决策方案后，系统能够快速诊断出故障表头并重新进行信息重构，故障信息不会被引入系统，且对系统的影响较小，入轨精度仍能够满足指标的要求，进而完成飞行任务。

5 结 论

运载火箭惯性导航系统有多种冗余方案。本文结合运载火箭工程实际应用情况，提出了一种基于十表捷联惯组导航系统的故障诊断和决策流程方法，并给出了具体的诊断算法。仿真结果表明，该方法能够覆盖1度故障并且兼顾部分2度故障，能够实现故障情况下导航及姿控信息的正常输出，具有一定的工程参考价值。