内环向加筋对功能梯度圆柱壳模态频率的影响
2022-01-04刘文光吕志鹏
刘 超,刘文光,吕志鹏
(南昌航空大学 航空制造工程学院,南昌 330063)
功能梯度材料(functionally graded materials,FGMs)是一种新型非均质复合材料,其结构内部组分随体积分数和空间位置变化而连续变化。其中,金属陶瓷功能梯度材料具有良好的耐热、隔热、缓和应力集中等优点,在航天飞机的结构设计中具有良好的应用前景。由于功能梯度材料的物理属性和传统复合材料或者纯金属材料的物理属性不同,使功能梯度结构的振动行为与材料的热物理属性变化密切相关。
基于不同的板壳理论,研究者对FGMs结构的振动行为开展了大量的研究。基于Love薄壳理论,Loy等[1]采用Rayleigh-Ritz法计算了两端简支FGMs圆柱壳的模态频率,Abdul等[2]采用能量法讨论了FGMs组分变化对FGMs壳模态频率的影响,刘文光等[3]探讨了考虑热应力后温度梯度对FGMs壳模态频率的影响,叶曦等[4]研究了热环境对FGMs壳频散特性的影响。基于Sanders薄壳理论,Qin等[5]研究了任意边界条件下FGMs壳的自由振动行为,Hashemi等[6]研究了不同边界条件下旋转速度对FGMs壳模态频率的影响。基于Donnell壳体理论,杜长城等[7]研究了FGMs薄圆柱壳的非线性自由振动,Hadi等[8]研究了热环境载荷作用下轴向、横向及热载荷对FGMs圆柱壳非线性振动的影响。基于Flügge理论,梁斌等[9]利用波动法研究了环肋FGMs圆柱壳在静水压力作用下结构固有频率随壳体几何尺寸、肋条尺寸和肋条数目等参数的变化规律。基于一阶剪切变形理论,Liu等[10]利用波动法研究了不同边界下FGMs圆柱壳的自由振动行为,Farahani等[11]利用波动法研究了流体中FGMs壳在静水压力作用下的振动,蒲育等[12]利用广义微分求积法研究了不同边界条件下FGMs梁的自由振动。基于高阶剪切变形理论,Punera等[13]讨论了FGMs开孔圆柱壳的自由振动,Song等[14]研究了热环境中碳纳米增强FGMs壳的振动,郝育新等[15]结合Galerkin法和Hamilton原理研究了材料非线性和几何非线性对FGMs板内共振行为的影响。
分析表明,FGMs结构的振动与其材料组分、热环境变化、结构几何尺寸等因素有关。但是,要推进FGMs在航天飞机圆柱壳设计中的应用,除考虑各种因素对FGMs圆柱壳振动行为的影响之外,还要保证圆柱壳在使用寿命范围内能够尽量节省材料。因此,开始有研究者探究加筋对FGMs圆柱壳振动行为的影响。基于经典薄壳理论,Dao等[16]研究了加强筋对FGMs圆柱壳振动特性的影响。基于Donnell薄壳理论,Phuong等[17]分析了加筋FGMs圆柱壳在热环境下的振动稳定性;基于一阶剪切变形理论,Sheng等[18]研究了热环境对加筋FGMs圆柱壳非线性振动的影响。
虽然研究者对加筋FGMs圆柱壳的振动开展了一些分析,但是鲜有分析采用高阶壳体理论讨论加筋变化对圆柱壳模态频率的影响。现有的文献中,研究者一般忽略圆柱体和加筋的剪切和旋转惯性。本工作主要采用三阶剪切变形理论推导加筋圆柱壳的模态频率方程,研究热环境下内环向加筋对FGMs圆柱壳模态频率的影响。
1 功能梯度圆柱壳模型
1.1 圆柱壳几何模型
加筋FGMs圆柱壳,圆柱壳的长度为L,厚度为h,圆截面的中面半径为R,如图1所示。在圆柱壳左端中面建立柱坐标系(x,θ,z),其中:x,θ和z分别为壳中面在轴向、环向和径向的坐标,u0,v0,w0分别为圆柱壳中面任一点沿坐标(x,θ,z)方向的位移。在圆柱壳的内表面设计若干条加筋,加筋的截面设计为矩形。假设第k条加筋位置距圆柱壳原点的距离xk,且加筋的宽和高分别为ak和bk。
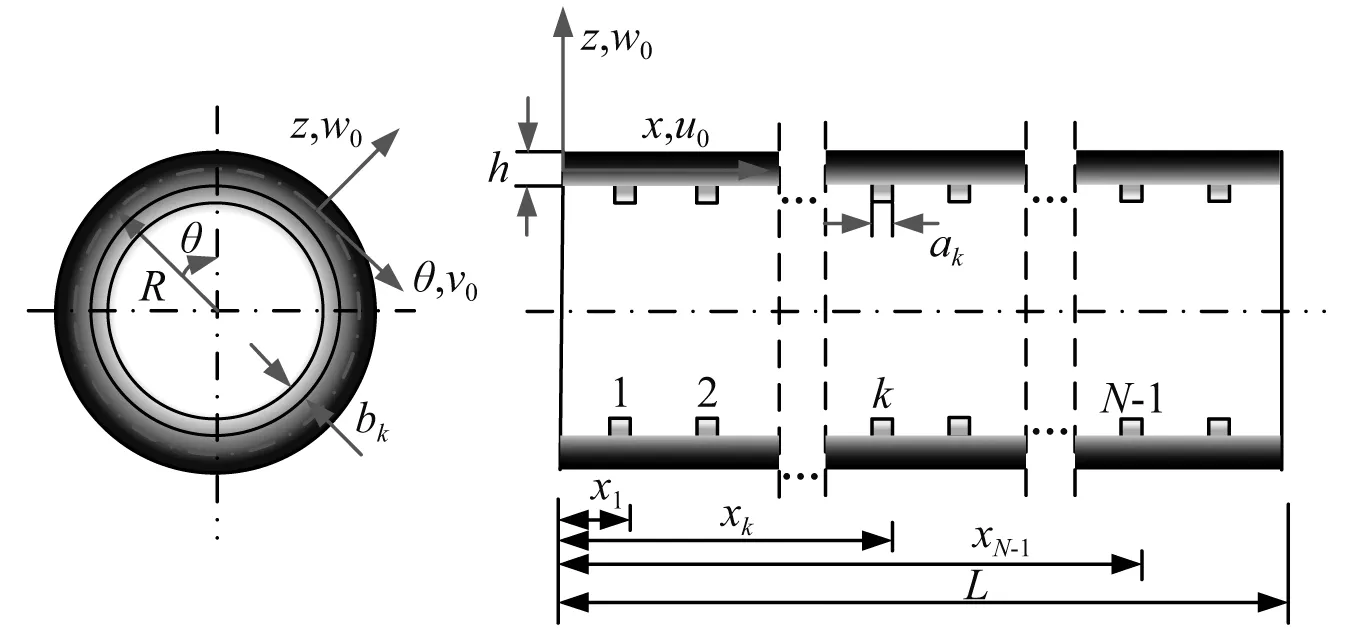
图1 加筋FGMs圆柱壳几何模型
1.2 功能梯度材料模型
假设FGMs圆柱壳的外表面为纯金属,内表面为纯陶瓷。根据Mori-Tanaka模型[19],FGMs的有效材料参数表达式为
(1)
式中:T为热环境温度;Gm和Gc分别为金属和陶瓷的剪切模量;Km和Kc分别为金属和陶瓷的体积模量;αm和αc分别为金属和陶瓷的热膨胀系数;Geff,Keff,αeff分别为FGMs的有效剪切模量、有效体积模量和有效热膨胀系数;Vm和Vc分别为金属体积分数和陶瓷体积分数(Vc+Vm=1),具体表达式与圆柱壳的加筋设计方法有关。
本文采用分离式和整体式两种方法对圆柱壳内表面添加加强筋。分离式加筋是指加筋和圆柱体采用不同的陶瓷体积分数。整体式加筋是指加筋和圆柱体采用相同的陶瓷体积分数。
对于分离式加筋圆柱壳,陶瓷体积分数表达式为
(2)
式中:Vc1和Vc2分别为加筋和圆柱体部分的陶瓷体积分数;ψ1和ψ2分别为加筋和圆柱体部分的体积分数指数。
对于整体式加筋圆柱壳,陶瓷体积分数表达式为
(3)
式中,Vc3和ψ3分别为加筋圆柱壳的陶瓷体积分数和体积分数指数。
取h/bk=5,ψi=1(i=1,2,3),分离式加筋和整体式加筋下FGMs圆柱壳的陶瓷体积分数沿厚度方向的变化规律,如图2所示。从图2可知,不同设计准则对材料组成与分布影响明显。因此,不可忽视设计准则对FGMs圆柱壳振动特性的影响。
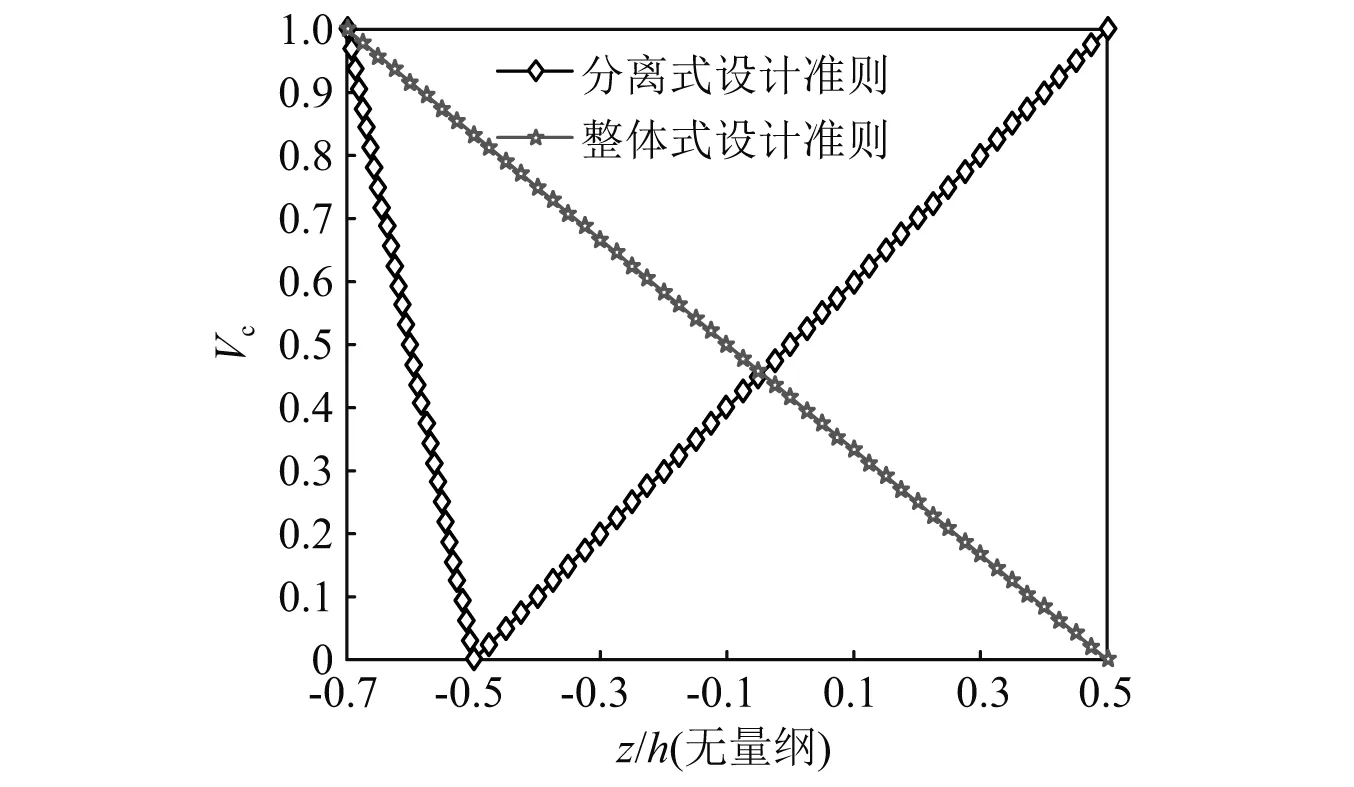
图2 陶瓷体积分数沿厚度方向的变化
根据剪切模量、体积模量与弹性模量和泊松比的关系,可推出加筋和圆柱体部分的有效弹性模量和有效泊松比
(4a)
(4b)
根据Voigt混合率模型,加筋和圆柱体部分的有效质量密度表示为
ρeff(z)=ρcVc(z)+ρm(1-Vc(z))
(5)
假设热环境下FGMs的物理属性与温度变化之间服从非线性关系[20]
pc,m=p0(1+p1T+p2T2+p3T3)
(6)
式中:pc,m分别为陶瓷和金属的物理属性(例如:密度ρ/kg·m-3、弹性模量E/GPa、泊松比υ、热膨胀系数α/1·K-1);p0,p1,p2,p3为材料的温敏特性系数,具体取值如表1所示。
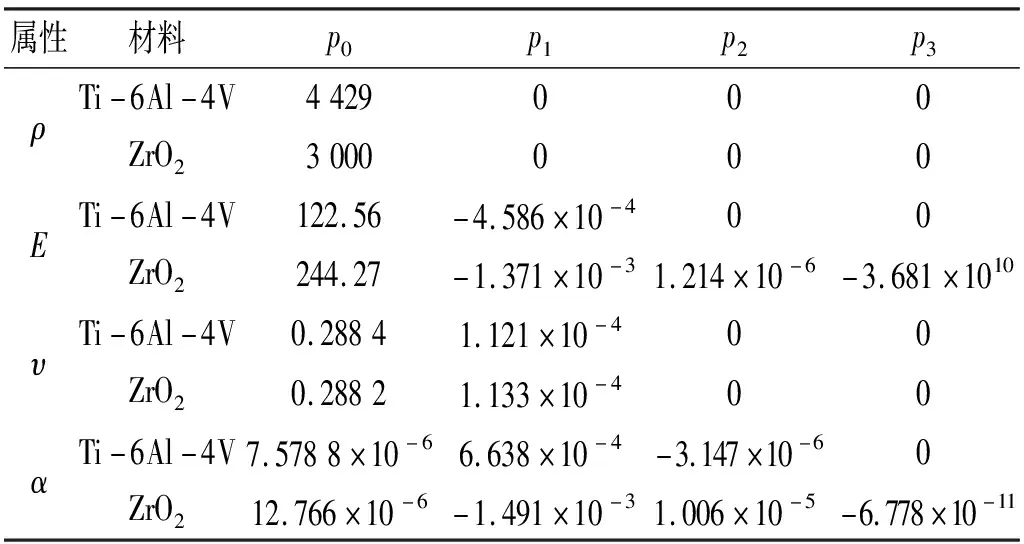
表1 ZrO2/Ti-6Al-4V温敏特性系数
考虑热环境下加筋圆柱壳温升沿厚度方向服从线性梯度变化形式
(7)
式中:Tcm=Tin-Tout为加筋圆柱壳最内层以及最外层的温差;Tin,Tout分别为加筋圆柱壳最内层、最外层被施加的温度;T0为环境温度(文中取T0=300 K)。
2 圆柱壳的模态频率方程
2.1 加筋圆柱壳的能量模型
根据二维胡克定律,加筋FGMs圆柱壳的应力-应变本构关系可以表示为
{σ}=[Q]{ε}
(8)
式中:{σ}为应力向量;{ε}为应变向量;[Q]为简化刚度矩阵。具体表达式为
{σ}={σxxσθθτxθτxzτθz}T
(9)
{ε}={εxxεθθγxθγxzγθz}T
(10)
(11)
式中:σxx,σθθ分别为x,θ方向的正应力;τxθ为xθ面内剪应力;τxz和τθz为厚度方向剪应力;εxx,εθθ分别为x,θ方向的正应变;εxθ为xθ面内剪应变,γxz和γθz为厚度方向剪应变;Qij(i=1,2,4,5,6)为简化刚度元素,定义为
(12)
考虑加筋和圆柱体的剪切和旋转效应,由三阶剪切变形理论得到加筋FGMs圆柱壳的位移场,具体表达式为[21-22]
(13)
式中:u1,v1,w1分别为圆柱壳内任一点沿x,θ和z方向的位移;φx和φθ为中面法线绕x和θ轴的偏转角。
加筋圆柱壳的弹性应变能等于
U=Us+Ur
(14)
式中:Us为圆柱体部分的应变能;Ur为加筋部分的应变能。具体表达式为
式中:若加筋和圆柱体厚度较小,则(R+z)可近似为R;δ(.)为Dirac函数;N为加筋的条数。
加筋圆柱壳的动能等于
K=Ks+Kr
(16)
式中:Ks为圆柱体部分的动能;Kr为加筋部分的动能。具体表达式为
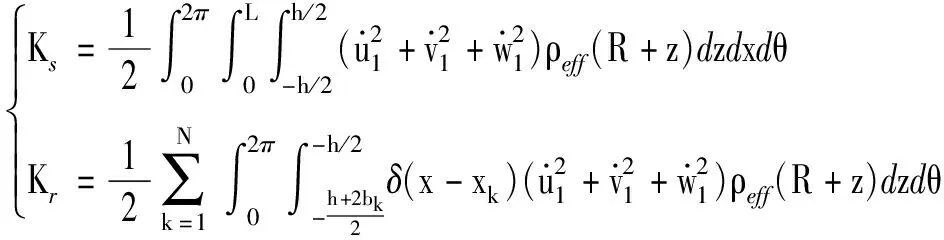
(17)
式中:ρeff为FGMs的有效质量密度;上标‘·’为对时间求导。
考虑热环境做功的影响,热载荷对加筋圆柱壳做的功能等于
W=Ws+Wr
(18)
式中:Ws为热载荷对圆柱体部分做的功;Wr为热载荷对加筋部分做的功。具体表达式如下[23]
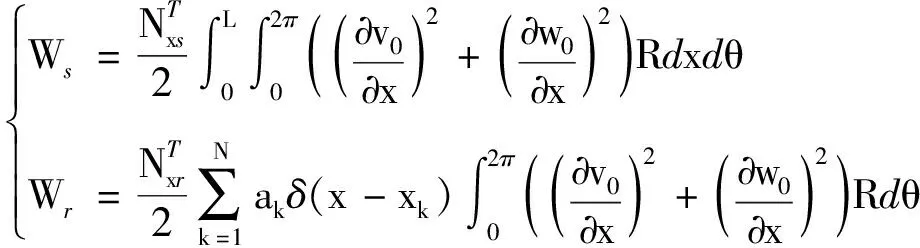
(19)
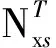
(20)
式中,ΔT(z)=T(z)-T0,为FGMs圆柱壳内任一点的温度与环境温度的差值。
2.2 Rayleigh-Ritz法
假设加筋圆柱壳中面振型函数为[24]
(21)
式中:ξ1,ξ2,ξ3,ξ4和ξ5分别为圆柱壳各个方向的振动幅值;m,n分别为圆柱壳轴向和环向波数;f为圆柱壳的模态频率。
根据Lagrange函数,加筋圆柱壳的能量函数为
Π=(Ks+Kr)max-(Us+Ur)max+(Ws+Wr)max(22)
式中,(Ks+Kr)max,(Us+Ur)max和(Ws+Wr)max分别为加筋圆柱壳的最大动能、最大应变能以及最大热载荷做功。取能量函数Π关于振幅的极值推导出模态频率特征方程。根据齐次方程组有非零解的充要条件得到关于模态频率的十次方程
a1f10+a2f8+a3f6+a4f4+a5f2+a6=0
(23)
式中,ai(i=1,…,6)为方程系数。
假设加筋等间距分布,且加筋圆柱壳由单一材料制成[25],其材料物理性能为:E=206.832 GPa,v=0.3,ρ=7 826.4 kg/m3。圆柱壳的几何尺寸为:R=0.103 7 m,h=0.001 2 m,L=0.942 m,加筋数量与模态频率的对比关系,如图3所示。
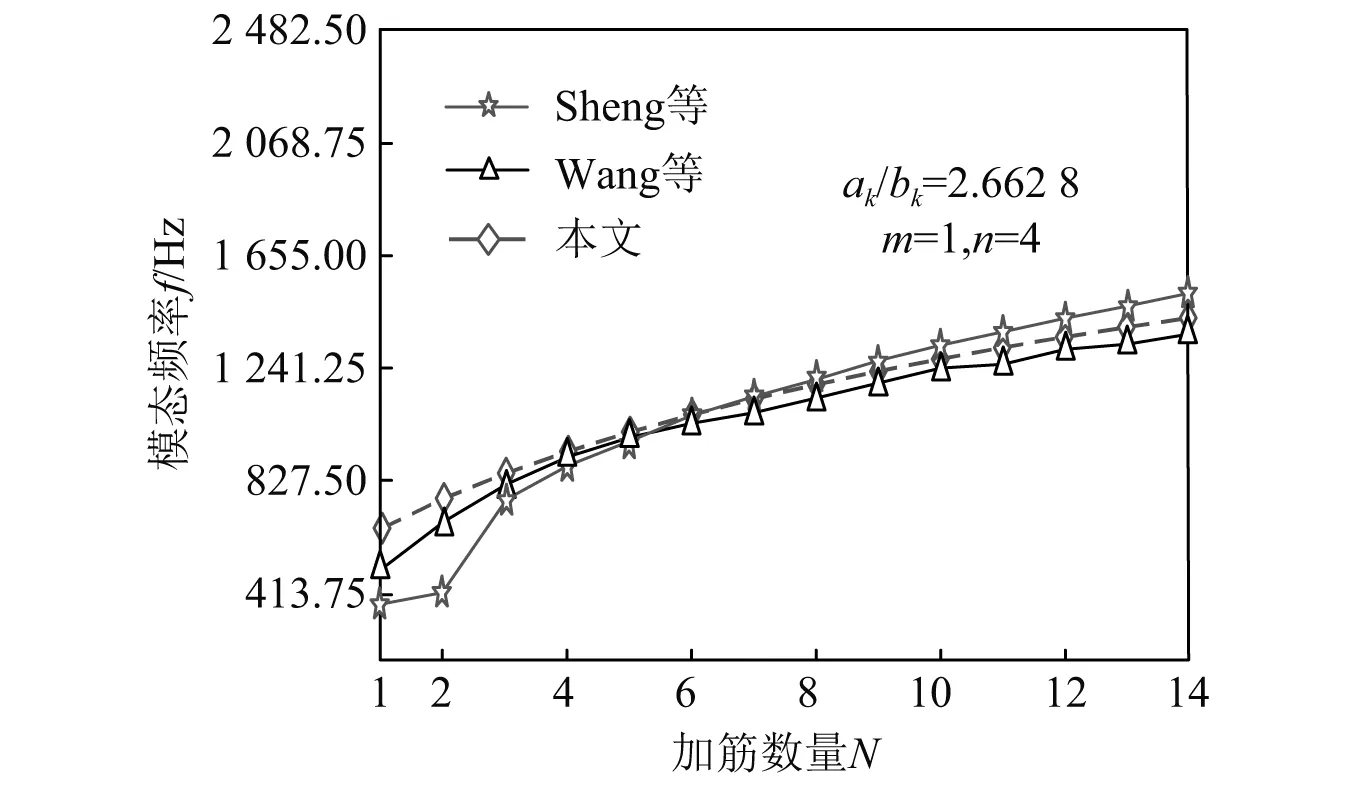
图3 加筋数量与圆柱壳模态频率的关系
从图3可知,应用本文模型计算加筋圆柱壳的模态频率与Sheng等、Wang等研究中的模态频率较吻合,说明上述推导模型有效。
3 加筋对FGMs圆柱壳模态频率的影响
如无特殊说明时,以下算例研究所用加筋圆柱壳的几何尺寸取:R=1 m,L=1 m,h=0.01 m,ak=0.01 m和bk=0.1 m;轴向振动波数m=1;加筋数量N=8;加筋为等间距分布。分析发现,陶瓷体积分数指数只影响加筋FGMs圆柱壳模态频率的大小,不改变加筋变化对模态频率的影响趋势。因此,以下讨论取圆柱壳和加筋部分的体积分数指数ψ=1,主要讨论加筋的设计方式、加筋数量和位置、加筋的宽高比等对圆柱壳模态频率的影响。
3.1 加筋的设计方式对模态频率的影响
有无热环境时加筋设计方式对FGMs圆柱壳模态频率的影响,如图4所示。
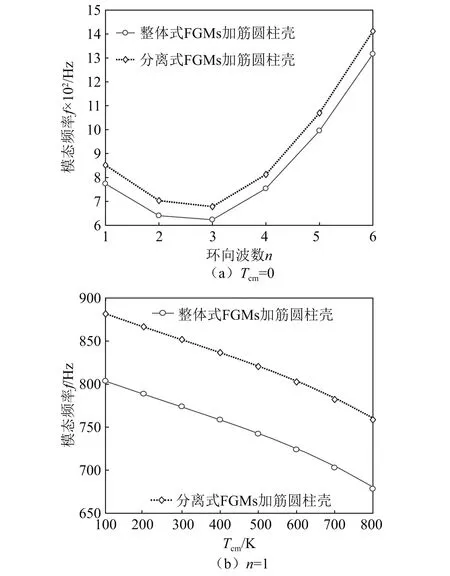
图4 加筋设计方式对FGMs壳模态频率的影响
从图4可知,不同环向波数下,分离式设计加筋FGMs圆柱壳的模态频率总是大于整体式设计加筋FGMs圆柱壳的模态频率;温度梯度增大,加筋圆柱壳的模态频率逐渐下降,且分离式设计对温度梯度敏感性相对更弱。因此,后续主要讨论分离式加筋FGMs圆柱壳模态频率的变化规律。
3.2 加筋数量对模态频率的影响
加筋数量N对FGMs圆柱壳模态频率的影响,如图5所示。从图5可知,在不同环向波数n下,模态频率随着N的增大基本呈现单调递增的趋势,但是模态频率并非随加筋数量的增大而成比例递增。当N达到约11时,模态频率逐渐收敛,特别当n=1时,圆柱壳的轴向振动频率随N的增大而逐渐减小。这说明加筋虽能提高结构刚度,但也会引起增加质量。进一步分析发现,N对低环向波数时模态频率影响较小,对高环向波数时模态频率影响较为明显。热环境下,当Tcm较小,N增大至14能有效提高模态频率;随着Tcm的增大,N对模态频率的影响越来越不显著,这说明N和Tcm对圆柱壳刚度的影响具有相互耦合的作用。结论表明,热环境下加筋的数目并非越多越好,加筋虽能提高圆柱壳的高环向模态频率,但这些模态频率并不主导圆柱壳的动力学设计。
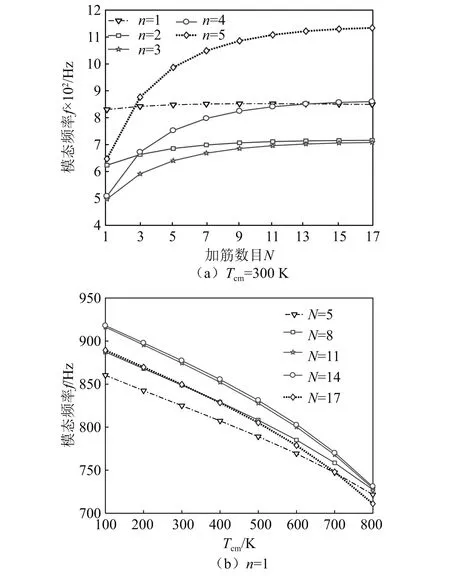
图5 加筋数目对FGMs壳模态频率的影响
3.3 加筋位置对模态频率的影响
除等间距加筋分布之外,加筋在圆柱壳轴向也可能非均匀分布。为了便于描述加筋的分布位置,定义加筋的位置函数xk
(24)
式中:xk为第k根加筋与圆柱壳左端原点距离;N为加筋数量,若N为奇数,则第((N-1)/2+1)根加筋在圆柱壳轴向中间位置。τ为非均匀位置参数,当0<τ<1时,加筋靠近轴向中心处较为密集分布;当τ= 1时加筋为均匀分布形式;当1<τ时加筋靠近圆柱壳的两端密集分布,具体分布形式如图6所示。
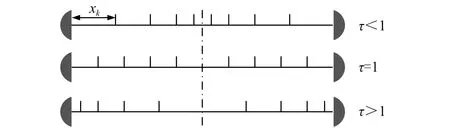
图6 加筋位置分布形式
加筋位置对FGMs圆柱壳模态频率的影响,如图7所示。
从图7可知,模态频率随着τ的增大呈先减小后增大的趋势,当0.4≤τ≤0.6时,模态频率出现最小。这说明加筋的分布越靠近圆柱壳两端或轴向中心越有利于提高模态频率。热环境下,模态频率随着τ的增大呈先减小后增大后又减小的趋势。当τ≤1时,Tcm对加筋布置在圆柱壳轴向中心处的模态频率影响较小,当1≤τ时,Tcm对加筋布置在圆柱壳两端的频率影响很大。总的来说,非均匀参数τ应尽量控制在τ≤0.4或1.2≤τ≤1.4内,适当调控加筋的分布位置可达到较大幅度提高圆柱壳模态频率。
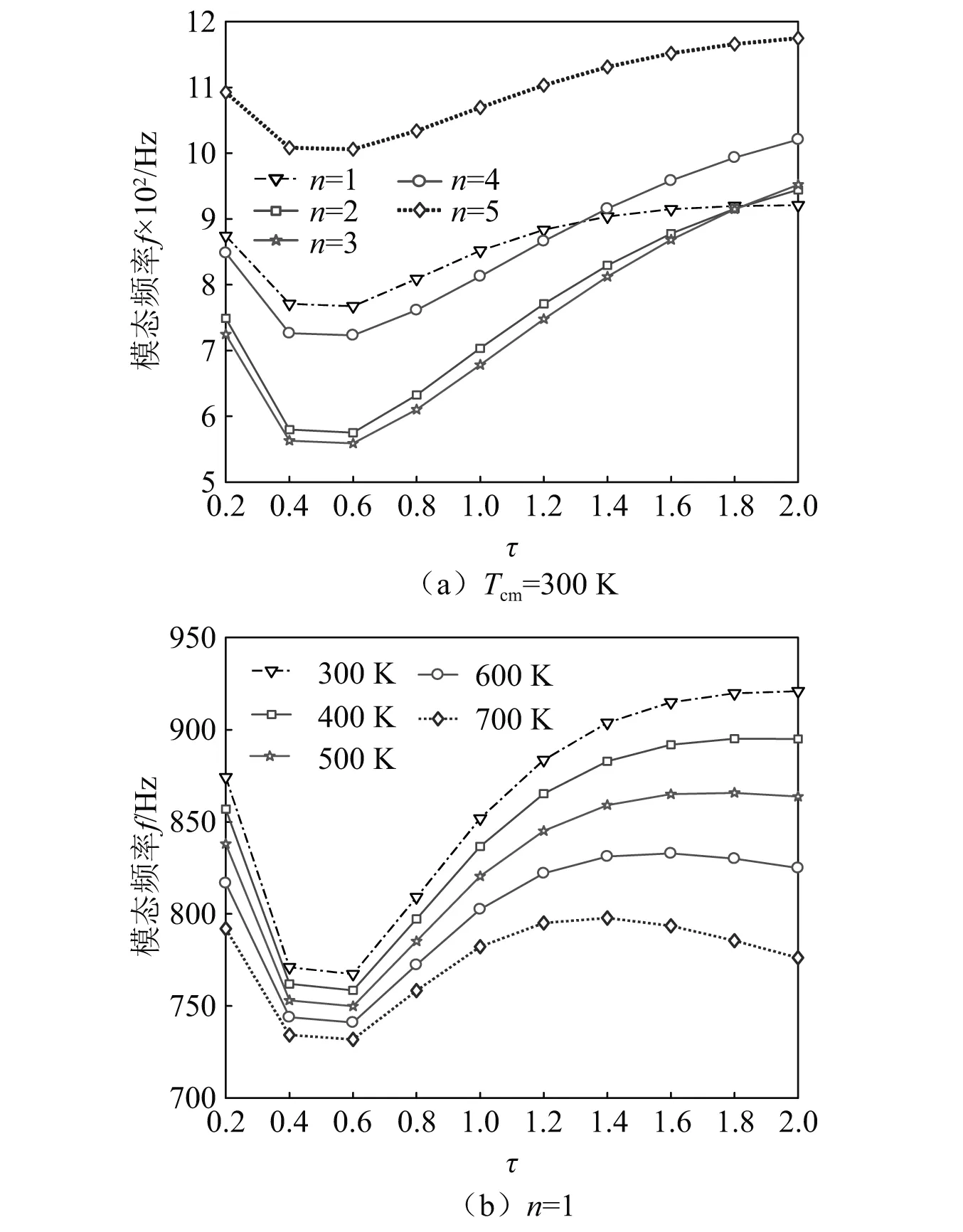
图7 加筋位置对FGMs壳模态频率的影响
不同壳体厚度下加筋位置对FGMs圆柱壳模态频率的影响,如图8所示。从图8可知,随着τ的增大模态频率基本逐渐增大,且非均匀参数τ对低环向波数的模态频率影响较大,高环向波数下影响较小。增大壳体厚度,环向波数大于4时,模态频率随着τ的增大逐渐减小。结论表明:加筋的非均匀位置参数τ对圆柱壳模态频率的影响较为复杂,圆柱壳的振动特性可能取决于加筋位置参数和圆柱体参数之间的匹配关系。
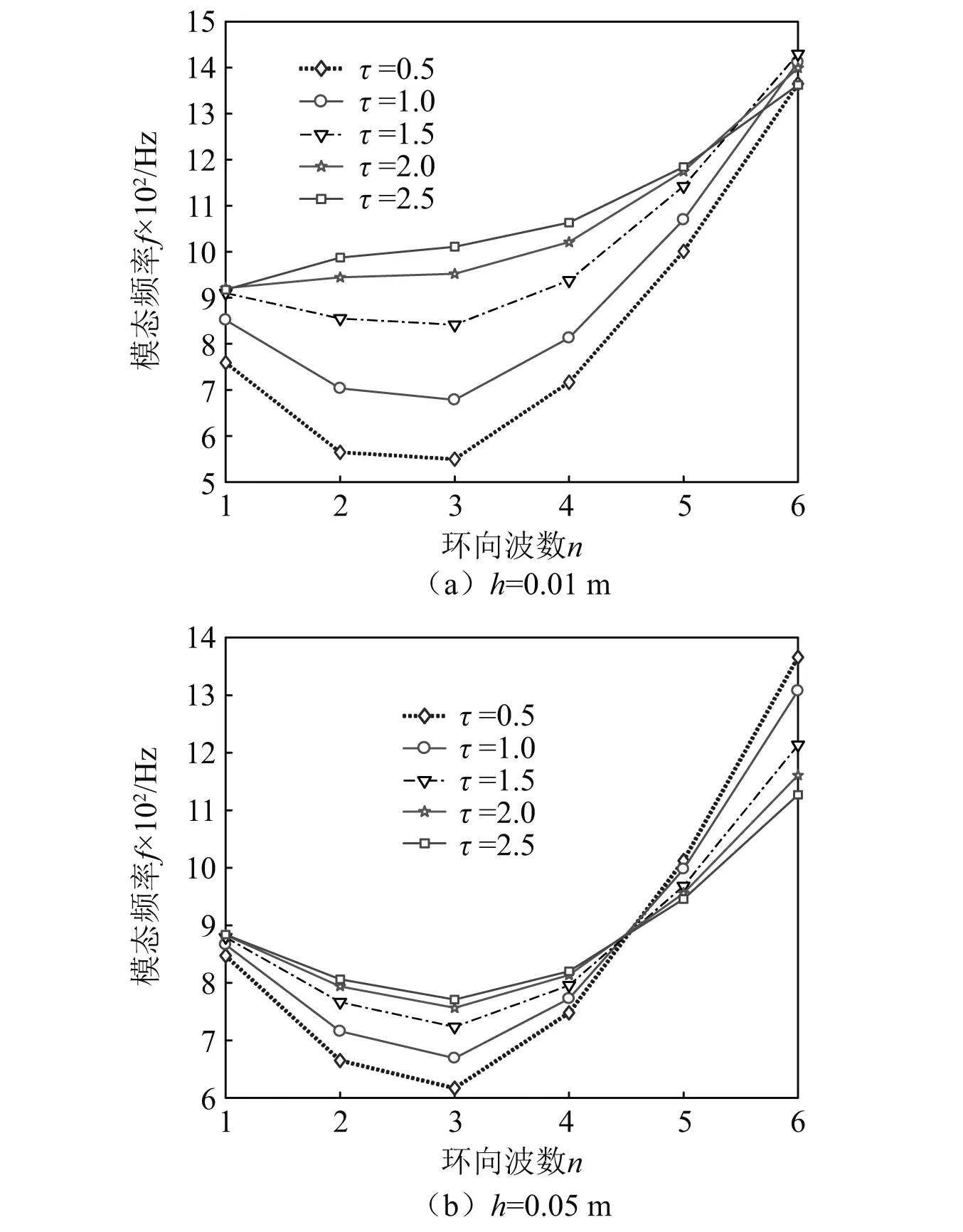
图8 不同厚度下加筋位置对FGMs壳模态频率的影响
3.4 加筋的宽高比对模态频率的影响
加筋宽度对壳模态频率的影响,如图9所示。从图9可知,当n=1或n=2时,模态频率均随ak的增大呈现先增大后减小的趋势;当n>2时,模态频率随着ak的增大呈现先增大后趋于稳定的趋势。在0.4≤ak≤1.3内,ak对模态频率的影响很显著。进一步分析可发现,圆柱壳的基频出现在n=3时,且在n=1和n=4时出现模态交叉现象,相应振型发生改变;当环向波数n=1时,模态频率在Tcm= 300 K时随着ak的增大呈现先增大后减小的趋势,而在Tcm>300 K时,模态频率随ak增大呈现单调递减的趋势。Tcm越大,圆柱壳的模态频率随ak增大而减小趋势越明显。因此,低温环境下,ak在0.4≤ak≤1.3内能一定程度提高圆柱壳的模态频率;高温环境下,温度梯度对圆柱壳刚度的贡献大于截面宽度对刚度的贡献,设计中应充分考虑温度梯度的影响。
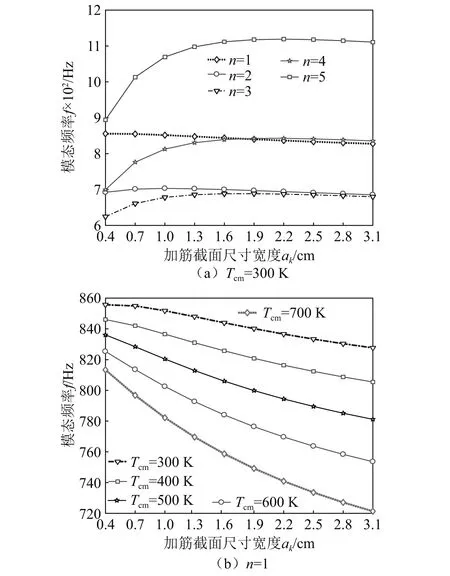
图9 加筋截面宽度对FGMs壳模态频率的影响
加筋高度对壳模态频率的影响,如图10所示。从图10可知,圆柱壳模态频率随着bk的增大呈逐渐递增的趋势。当1
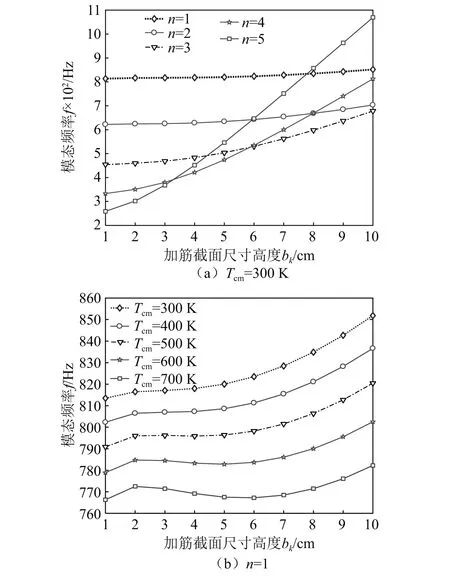
图10 加筋高度对FGMs壳模态频率的影响
加筋在同一截面面积下,宽高比对圆柱壳模态频率的影响,如图11所示。从图11可知,ak=0.01 m,bk=0.1 m和ak=0.1 m,bk=0.01 m条件下,圆柱壳的模态频率的差值随着环向波数增大而增加;ak=0.2 m,bk=0.005 m和ak=0.1 m,bk=0.01 m条件下,圆柱壳的模态频率差值很小;ak=0.005 m,bk=0.2 m和ak=0.01 m,bk=0.1 m条件下,模态频率差很大。这说明加筋的截面高度bk相对截面宽度ak对圆柱壳的刚度更为敏感,工程中应尽量注重截面高度的合理设计,并选用较大的截面高度以提高圆柱壳基频。
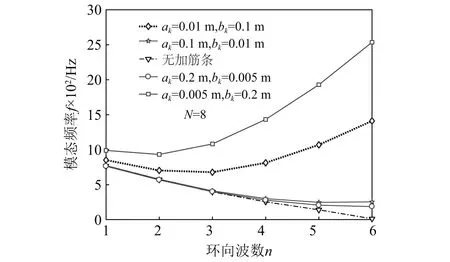
图11 加筋截面宽高比对FGMs壳模态频率的影响
4 结 论
考虑加筋圆柱壳的剪切和旋转效应,计算了加筋圆柱壳的应变能、动能和热载荷做功。利用能量函数推导了加筋圆柱壳的模态频率方程。探讨了加筋的设计方式、数量和位置、截面变化等对圆柱壳模态频率的影响。主要得到以下结论:
(1)分离式设计加筋相比整体式设计加筋对提高圆柱壳的模态频率更为有利,而且对温度梯度的敏感性更弱。
(2)加筋越多越能提高圆柱壳的模态频率,但模态频率的增加与加筋数目的增大并非比例关系,当加筋数目约为11时,模态频率趋于稳定。
(3)加筋位置参数τ在τ≤0.4或者1.2≤τ≤1.4内更有利于提高圆柱壳的模态频率,且加筋的非均匀位置参数和圆柱壳参数之间存在匹配关系,对加筋圆柱壳模态频率的变化规律影响较复杂,在圆柱壳结构设计中应当注意。
(4)加筋截面的高度相对截面宽度对圆柱壳刚度更为敏感,低温环境下0.4≤ak≤1.3时能提高圆柱壳模态频率;但在高温环境下,温度梯度对圆柱壳刚度的贡献大于截面宽度对刚度的贡献,设计中应充分考虑温度梯度的影响,此时应从增大截面高度的角度提高圆柱壳的模态,避免圆柱壳在高环向波数下发生共振。
