极地车辆车轮与雪壤交互作用模型研究综述

闫清东, 科蒂耶夫, 魏巍,3*, 朱明, 陈修齐, 张渊博,郑浩泉, 扎哈罗夫, 伊尔西耶夫, 柯西琴, 戈卢布奇克,斯塔杜欣, 郑怀宇

(1.北京理工大学 车辆传动国家重点实验室，北京 100081；2.俄罗斯莫斯科国立鲍曼技术大学 轮式车辆系，莫斯科 105005；3.北京理工大学 重庆创新中心，重庆 401120)

北极地区富含矿产资源和其他各类自然资源，但冬季平均气温约为-22.3 ℃，极限低温达-60 ℃以下，多数季节积雪覆盖，局部深度甚至超过2 m.车辆在极地环境下的性能面临着极大的考验[1].对极地雪的力学性能的理论、试验以及数值仿真的研究，是研究极地车辆在极地雪壤环境行驶动力学性能的基础.极地车辆大多采用履带或者低压轮胎作为行走机构，行走机构与雪壤间的相互作用直接决定车辆行驶性能，也是提高极地环境下车辆通过性的基础.

文中针对高纬度地区可变性组分雪壤，在雪的力学特性理论及试验研究基础上，总结分析了车轮-雪壤复杂交互过程的经验模型、解析模型和离散元/有限元数值模型进行概括，提出了轮-雪交互作用进一步研究方向.

1 雪的力学特性模型

在高纬度严寒地区，车辆在积雪地形行驶时，轮胎与雪壤的交互过程较为复杂，其复杂性是由诸多不确定性因素造成的，如雪的密度、微观结构、含水量和温度等影响雪材料特性的因素，以及宏观堆积状环境、雪块的碎裂与重结晶、考虑雪深的支承面轮廓等[2].其中密度通常是表征雪力学性能最常用的参数，但由于雪的微观结构对雪的力学性能的影响较大，仅用雪密度作为单一评价指标来表征雪地行驶特性是不够的.

1.1 粘弹性力学模型

雪是粘弹性的物质，当施加在雪上的外力(压力)足够小的时候，不会发生断裂以及破坏.M.de Quervain[1]通过在实验室进行雪柱实验来研究雪的粘弹性，最终得出雪的力学特性可由一个Maxwell单元模型和一个Voigt单元模型串联，以及应力松弛时间τ构成的流变力学模型来定性表示，如图1所示.Maxwell单元模型由一个弹性单元与一个阻尼单元串联组成；Voigt单元模型由一个弹性单元与阻尼单元并联组成.

图1 代表雪压缩特性的流变力学模型

日本北海道大学低温科学研究所的相关学者[3]对模型中的参数进行了定量研究.以下关系式是弹性模量E(MPa)和粘性阻尼常量C(MPa·min)在不同温度条件下与积雪密度ρ(kg/m3)关系的经验公式.

1)E1和C1的确定

当环境温度为-1～-3 ℃时，

E1=-1.5+(0.04/3)ρ，

(1)

1/C1=2-0.006 5ρ.

(2)

当环境温度为-5～-15 ℃时，

E1=-5.4+0.036ρ，

(3)

1/C1=0.85-0.003ρ.

(4)

2)E2和C2的确定

当ρ=100～200 kg/m3时，环境温度高于-1.5 ℃，E2约为E1的2～4倍，C2约为C1的0.7～0.91倍.

当ρ>200 kg/m3时，环境温度低于-10 ℃，E2小于2E1，C2约为C1的0.11倍.

3)τ1和τ2的确定

材料在恒定应变下，应力随着时间的变化减小到某个有限值的过程称为应力松弛，这是材料结构重新调整的一种现象.

应力松弛时间τ1=C1/E1约为4～15 min，松弛时间τ2=C2/E2约为0.5～1 min.

在某些情况下可以用Maxwell简化模型来表示雪的粘弹性模型，相关参数分别记为EM、CM、τM.

(5)

CM=C1,

(6)

τM=CM/EM=(C1/E1)+(C1/E2)=
τ1+(C1/C2)τ2,

(7)

应力松弛时间τM通常为8～30 min.由流变力学可知，Maxwell模型构成的物质表现出的力学性能，在作用时间小于τM时，为类固体物质；大于τM时,为类液体物质.

1.2 压力-沉陷经验模型[3]

在某一下陷深度下，雪可以承载一定范围内的压力，而不是单一的压力值.文献[3]利用自动记录负载支撑强度和下沉深度的装置(如图2所示)来确定雪在特定下陷量下的压力宽度，并进行近似拟合，得到了雪承受压强受下陷量影响的函数关系：

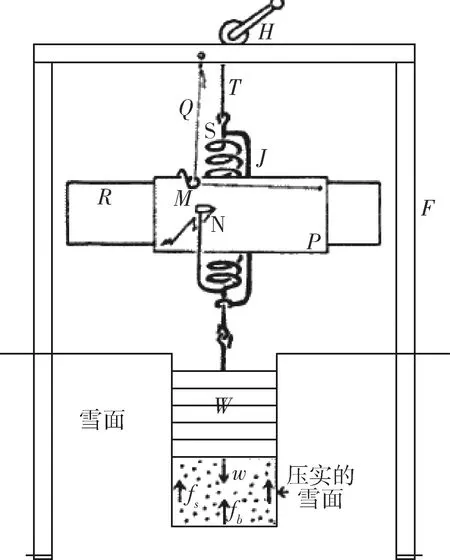
图2 自动记录负载支撑强度和下陷量的装置

pm=4+1.70D+ 0.28D2，

(8)

式中：pm为雪的压强，100pa；D为雪的下沉量，cm.

Alger[4]分别在实验室与野外进行的圆盘加载试验表明：在测量雪的下陷量时，由于雪的性质易变，受密度、时间、雪的类型和地区的影响较大，只有初雪的性质差别较小，所以，一般取初雪进行测试.测试的试验数据用来验证有限元模型中雪的不同材料属性，其中，实验室数据与有限元模型曲线较为符合，特别是与Modifified Drucker-Prager Cap(MDPC)模型(在1.3节中介绍)更加接近，而野外测试与实验室测试偏差较大，野外测试的影响因素更加复杂.

袁永丽[5]在实验中直接将不同质量的重物轻放在雪面上，测其自由下陷距离，得到雪的下陷量与压强的多项式曲线拟合方程为

P=0.049D2+111.5D+18.6，

(9)

式中：P为压强，pa；D为雪的下陷量，mm.

虽然该方法的测试结果可以作为雪地车的设计依据，但由于试验方法简单，试验中重物下放存在惯性力和动载荷，试验数据偏大，近似线性的结果和上文的经验公式存在较大差别.

1.3 压力-沉陷数值计算模型

参考板压痕理论[2]的观点，将轮-雪交互过程抽象地分为3个阶段：第1个阶段为弹性变形，发生于零压力、零下陷起始点到压力接近材料(雪)的内聚压力，可视为线性过程的弹性变形；第2个阶段为发生于材料(雪)开始屈服时，在接触物(轮胎)的底部将形成球状压力面，如果雪的深度足够，则一直会硬化传播到雪的底部，此过程为塑性变形过程；第3个阶段发生在达到有限的深度后，表现为弹性变形.

根据接触力学，压头下的应力状态可类似视为腔体膨胀问题，即将受压雪面视为内部压力作用下的厚壁圆柱或球形压力容器.图3示出了应用于具有3个区域压痕问题的接触力学的概念：芯部是位于压头正下方的区域，该区域可能具有准单轴应力状态；中间区域是塑性变形区；外围则是一个弹性变形区.

图3 压痕试验的变形区域

这样可将芯部区域建模为空腔，即由压头在图3的芯部区域中引起的压力建模为空腔的内部压力；芯部区域的其余部分建模为压力容器.通过解决空腔膨胀问题，计算给定载荷下塑性区域和弹性区域中的应力，即随着载荷的增加，塑性区域将膨胀.对于半无限域，塑性区将无限增加，直到达到材料的破坏强度为止；对于有限域，塑性区域可以增加，直到整个域变为塑料或达到材料的破坏强度为止.

适用于轮-雪交互作用下的雪的破坏屈服准则：Mohr-Coulomb(MC)屈服准则是考虑了正应力或平均应力作用的最大主剪应力或单一剪应力屈服理论，Drucker-Prager(DP)屈服准则可以看作是MC屈服准则的三维推广.改进的Drucker-Prager模型-Modifified Drucker-Prager Cap(MDPC)模型-与MC屈服准则相比更加细致，两者都有粘聚力和剪切角.空腔膨胀的求解是基于MC屈服准则的，MDCP模型适用于数值模拟.文献[6]研究的上限压痕理论使用了简化的DP屈服准则，其屈服条件可以写成

(10)

此外，有多种方法可以表示压力相关屈服面.一般认为，屈服面与材料的拉伸和抗压强度(C，T)的绝对值直接相关.

(11)

式中：C为材料的拉伸强度;T为材料的抗压强度.

图4 有限元模型

总结以上关于雪的力学特性模型的描述，雪的粘弹性力学模型引入了应力松弛时间，来表征雪的应力应变的时变效应，适用于长时间轻载下雪的力学特性的研究；压力-沉陷经验模型注重雪的宏观力学特性研究，多项式拟合的关系可以为车辆在雪地中的行驶提供相对可靠、实时性强的载荷值，但雪在特定下陷量的压力受时间、地区等的影响较大，只有初雪的差别较小；特定下陷量下存在压力宽度的轮-雪交互特性，研究文献较少；压力-沉陷数值计算模型提供了用于有限元计算材料弹性、塑性以及破坏时的材料属性，可以提供车辆行驶过程中雪壤的应力分布，准确地模拟车辆行驶过程中雪壤的力学行为.

2 轮-雪交互模型

2.1 轮-雪接触经验模型[7]

文献[8]提出了浅层雪机动性模型，主要针对简化模型-单个牵引元件进行建模，提出单轮胎或履带在浅雪表面行驶时积雪压实产生的阻力(Rs)经验公式：

当ρ0<ρf(z>0)时,

(12)

当ρ0=ρf(z=0)时，

Rs=0，

(13)

式中：p为轮胎充气压力，100pa；b为轮胎或履带最大宽度，m；h为雪深，m；ρ为给定轮胎通过后雪的密度，kg/m3；ρ0为雪的初始密度(轮胎或履带通过前)，kg/m3；ρf为雪的最高(最终)密度(车辆通过后)，kg/m3；z为下陷量，cm.

轮胎或履带与雪面的相互关系可由图5来描述.

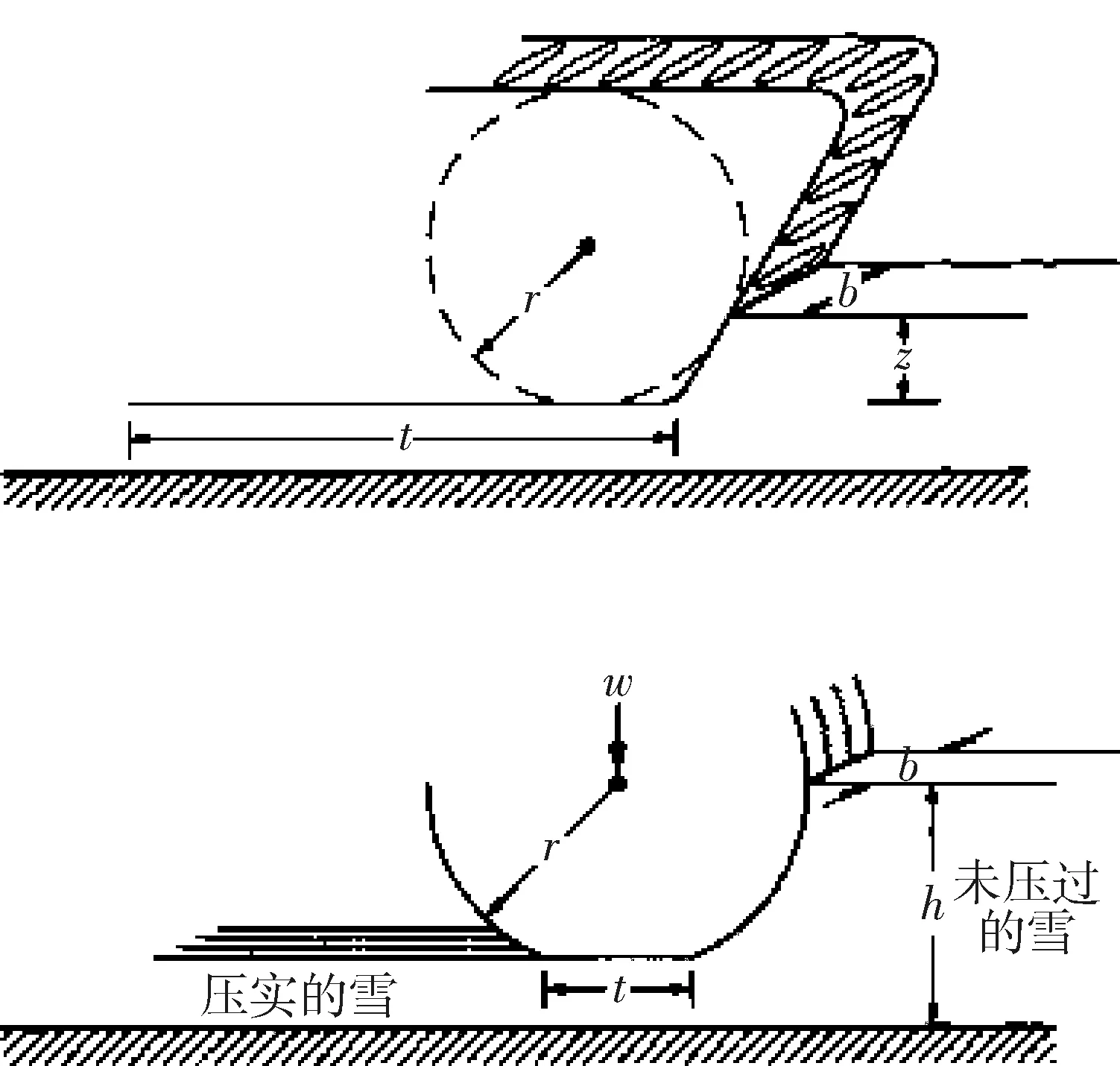
图5 履带和轮胎与雪壤交互作用关系示意图

压实部分是轮胎施加在雪地表面的垂直力(车辆重量)的结果；然而，压实是沿着弯曲的路径进行的，因此，也会施加水平力.压实功等于外部运动阻力乘以水平行驶距离.在这一经验公式，存在以下假设：首先，假设在压实过程中雪的横向流动不明显(即压实仅限于轮胎或履带的宽度)，雪的体积变化可以用下沉量z表示.其次，假设在压实过程中雪的总质量没有变化，那么雪的初始和最终体积可以用雪的初始密度和最终密度表示.

而牵引力Tg由公式拟合：

Tg= 0.851N0.823，

(14)

式中：N为轮胎或履带给地面的法向应力，kpa.此方程仅限于雪面未受干扰条件下的轮式或履带车辆.

文献[9]在整车机动性模型中对轮-雪压力-密度关系进行拟合，并将轮胎、履带与雪面交互的过程分解为离散过程，分别用经验公式进行拟合.

首先假设车辆通过时所产生的最大下陷量可以通过式(15)计算获得：

(15)

式中：h0为未压过雪的深度，m；ρf为雪的最大(最终)密度(车辆通过后)，kg/m3.假设zmax和ρf会出现在车辆施加的压力达到最大的时候，则ρf是由车辆上轮胎或履带所施加的最大压力来确定.ρf可由表1作为参考来选取.

表1 SSM 2.0中雪的最终密度

将车辆在雪面上的行进过程离散化表示，那么车辆前进的每个时刻所对应的相关参数如图6所示.

图6 轮胎通过雪面时雪面的渐进变化

由于雪受到的压力与下陷量的关系不是线性的，假设他们之间存在幂函数关系，对于接触压力小于pmax的轮胎或履带来说，下陷量z可由式(16)来确定：

(16)

式中：zmax为雪的最大下陷量，cm；pmax为雪在压实过程中受到的最大压力，kg/m3；p为雪在压实过程中受到的压力，kg/m3.

将车辆在雪面上的行驶过程分解为多个过程后，第i时刻前进的下陷量z可由下式确定：

当ρi>ρi-1,ρi-2,...ρ0时，

(17)

当ρi≤ρi-1,ρi-2,…ρ0时

zi=0.

(18)

式中：ρi、zi分别为在第i时刻雪的密度和雪的下陷量.

为计算运动阻力Rs，我们需要知道任意i时刻雪的密度ρi，因此,基于前面所给出的公式以及假设，可以给出：

(19)

式中：ρi-1和hi-1为i-1时刻车辆通过雪面时，雪的密度和深度，zi为i时刻的下陷量.

由于轮式或履带车辆不可能一直在未受压的雪面上行驶，或者沿着之前压实形成的通道行驶，又或者更为复杂的情况.我们需要考虑轮胎或者履带有一定比例的宽度具有在新雪上通过的可能性，而其余的宽度上则在以前压实形成的通道行驶.因此，Rs和Tg的方程修改为：

当ρi>ρi-1时，

(20)

当ρi=ρi-1时，

(21)

当ρi<ρi-1时，

Rsi=0,

(22)

Tg=0.851N0.823.

(23)

2.2 轮-雪接触解析模型

图7展示了简单的轮胎-雪面交互模型中的一系列重要参数.其中，雪壤的材料属性采用1.3节提到的Drucker-Prager模型.在车辆行驶过程中，给定车轮施加扭矩Tapp(My)，产生了角速度w和纵向速度v，轮胎半径为r，传递给轮胎的垂直载荷为Fz.未变形积雪深度为hs，轮胎下沉深度为Z0.在轮-雪接触表面,接触剪应力为τ，接触正应力为σn，由于τ产生的力的水平分量定义为牵引力Fτx.类似的，由σn产生的力的水平分量定义为运动阻力Rx.

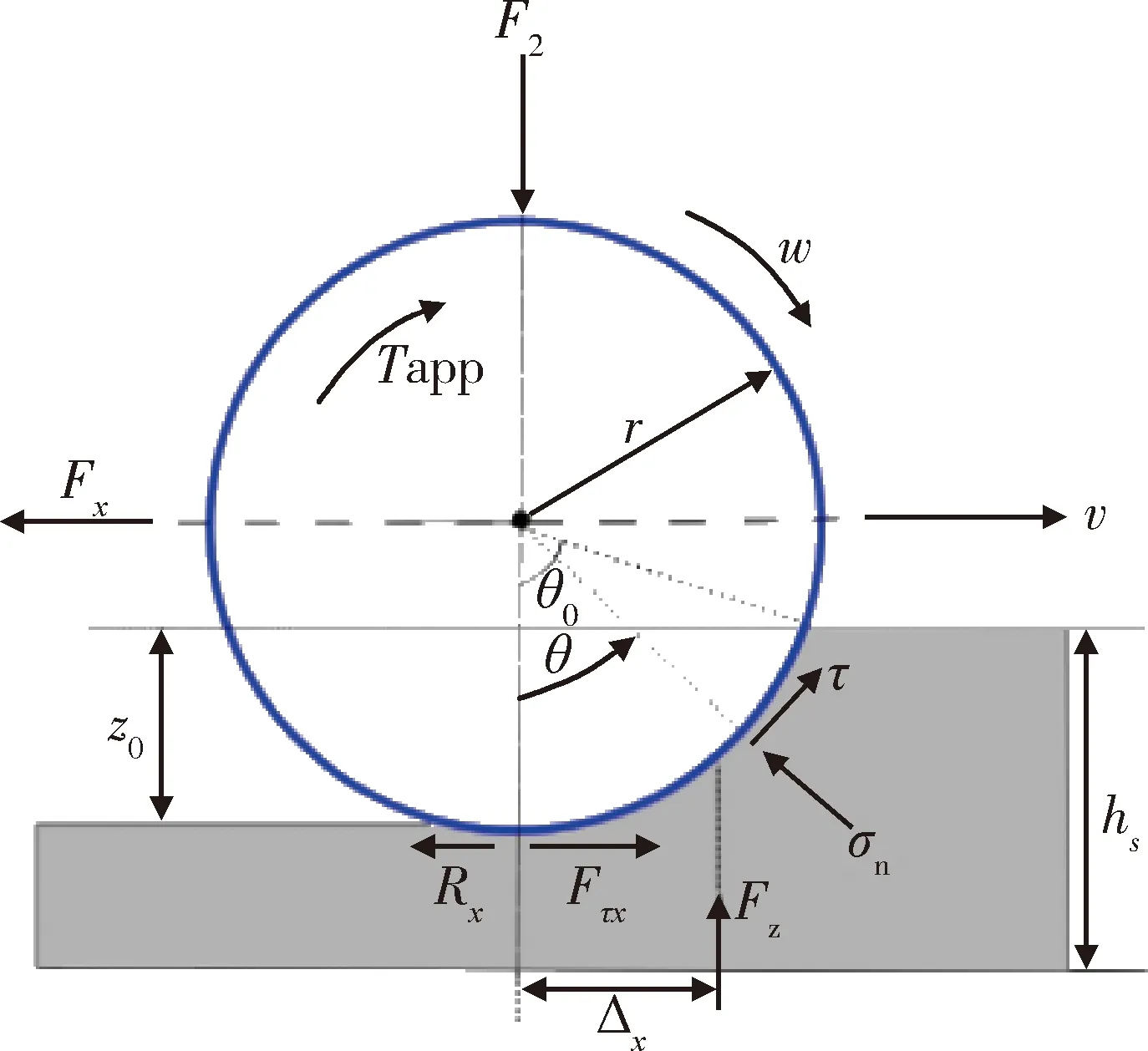
图7 轮-雪交互解析模型

运动阻力定义如下：

(24)

牵引力定义如下

(25)

式中：b为轮胎接地面的宽度;r为车轮半径;frr为轮胎滚阻系数.

合牵引力Fx由Fτx和Rx的之和表征：

Fx=Fτx+Rx.

(26)

2.3 轮-雪接触有限元模型[9-11]

轮-雪交互作用状态受很多因素的影响，比如驱动或制动时的纵向滑移、转向时的侧向滑移、制动转向时的组合滑移、轮胎的法向载荷、界面摩擦系数等.文章[12]对有限元仿真中的雪壤材料使用改进的Drucker-Prager模型-Modifified Drucker-Prager Cap(MDPC)，对不同的垂向载荷、全域纵向、侧向滑移工况下的轮-雪交互作用进行了有限元仿真，对运动过程中的界面力、下陷量、车轮状态、接触应力、接触剪应力以及雪密度等状态量进行了分析.

根据轮-雪交互作用力和车轮的滑移状态，确定的车轮运动状态如图8所示.

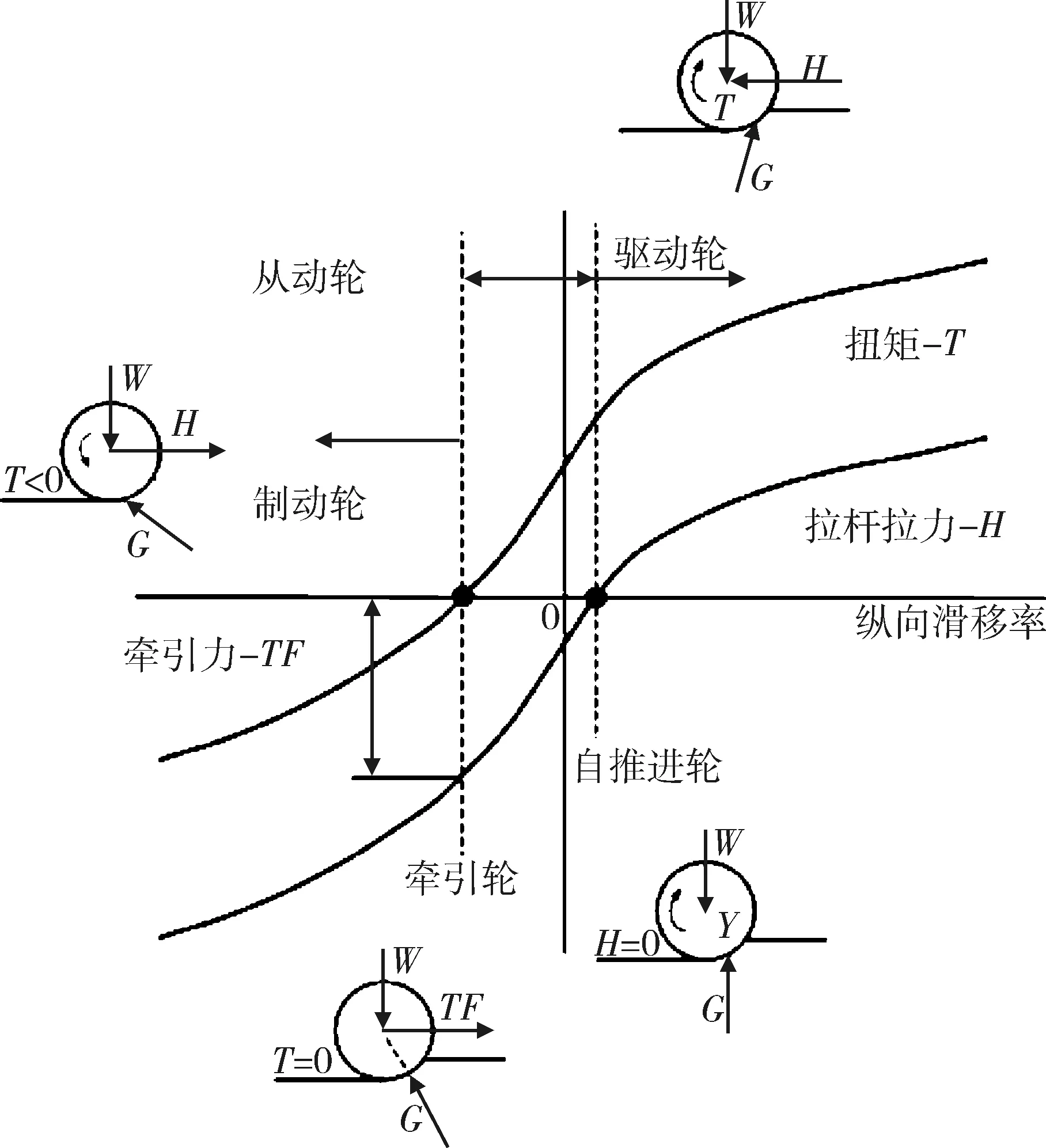
图8 轮胎状态

图中，水平轴是纵向滑移ix；垂直轴是拉杆拉力(H)或扭矩(T)；TF是牵引力；W(Fz)是施加在轮胎上的垂向力;G是接触力的合力.

当车轮上的驱动转矩T为零时，车轮此时的状态称为牵引状态，牵引力与运动阻力大小相等，方向相反；当拉杆拉力为零，驱动转矩大于零时，车轮此时的状态称为自推进状态；纵向滑移率小于牵引轮状态时，车轮处于制动状态；纵向滑移率介于牵引轮和自推进轮的车轮状态称为从动轮状态；纵向滑移率大于自推进状态时的车轮状态称为主动轮状态.

对于轮-雪交互作用下的界面力而言，驱动力、运动阻力以及合牵引力与纵向滑移率的关系如图9所示.

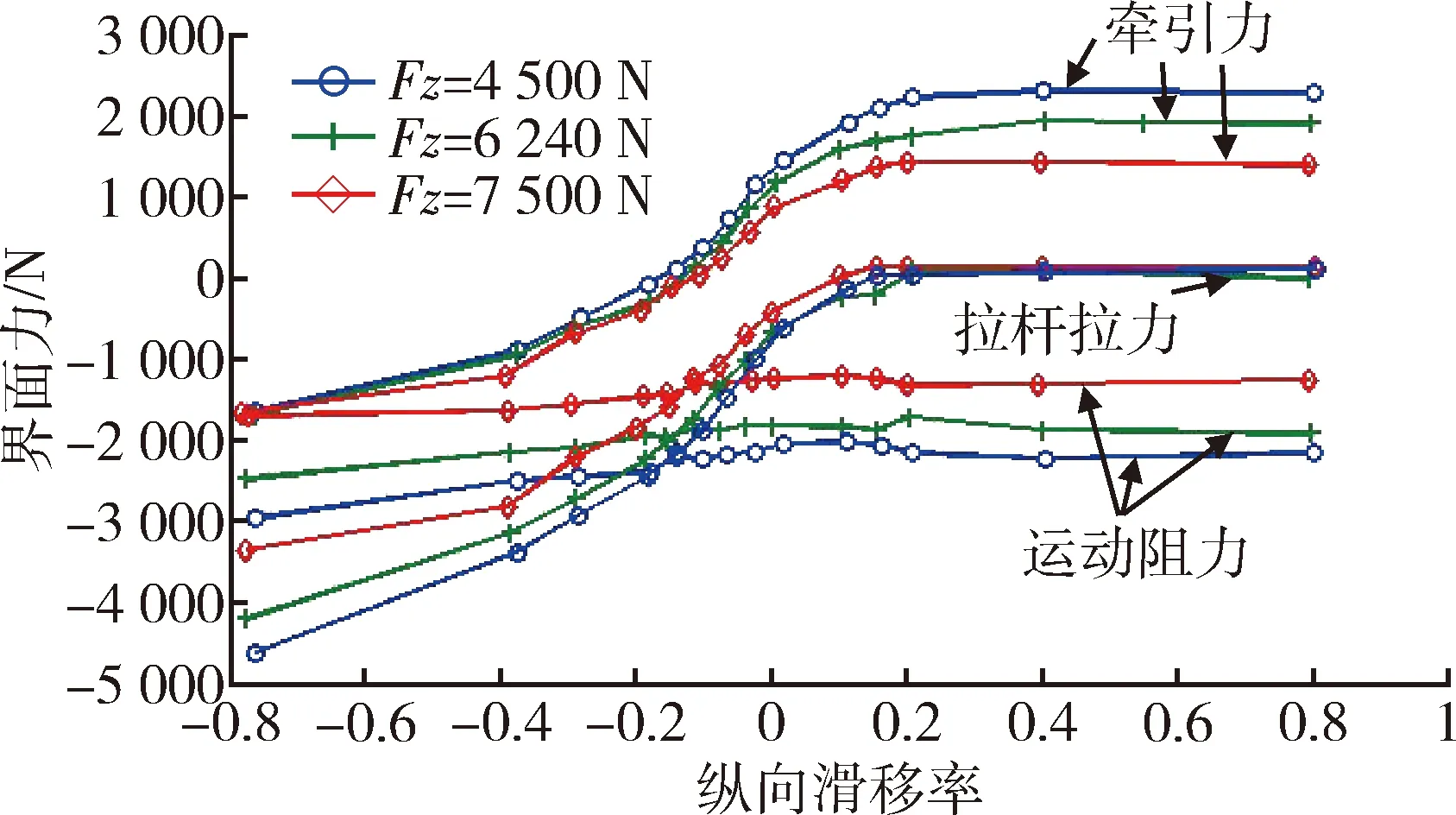
图9 界面力与纵向滑移率的关系

车轮处于制动状态时雪壤的下陷量要大于车轮处于其他状态时的下陷量.不同垂向载荷下的下陷量随纵向滑移率的关系如图10所示；同一垂向载荷不同侧偏角下的下陷量与纵向滑移率之间的关系如图11所示.

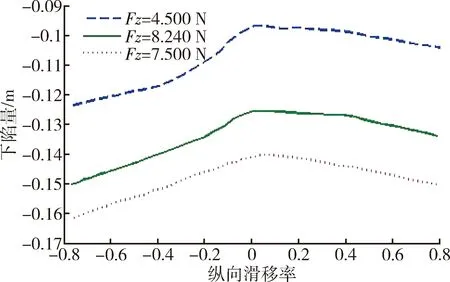
图10 雪的下陷量与滑移率的关系

图11 不同侧偏角下下陷量与纵向滑移率间的关系

对于接触剪应力而言，轮-雪交互作用下的雪壤表面存在4个明显的区域，如图12所示.在车轮处于制动状态时，区域1为正应力：由于轮胎向前运动，轮胎外表面与雪地接触而产生的正应力；区域2为负应力：由于轮胎向前运动导致轮胎前部与雪接触而产生的负应力；区域3为负应力：轮胎旋转产生了正的滑动位移，轮胎底部与雪接触产生的负应力；区域4为正应力：轮胎旋转产生了负的滑动位移，轮胎底部和积雪接触产生的正应力.

图12 不同行驶状态下的雪壤的剪应力分布

对于制动轮而言，剪应力沿着纵向界面从负变为正，最大剪应力发生在车轮前后缘；对于从动轮而言，只存在区域1-3；对于驱动轮而言，只存在区域4.

对于轮-雪交互作用下的雪密度分布，文献[13]将试验结果和有限元法仿真结果进行了比较.雪密度分布的试验值和仿真结果趋势一致，最大误差发生在胎肩处，仿真值大于实验值，误差为25%；在轮胎正下方，仿真值小于实验值，误差为10%.见图13.

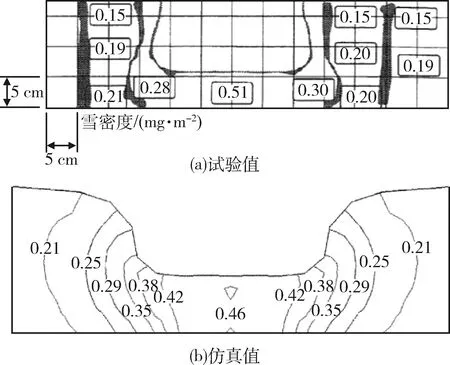
图13 雪密度分布的试验和仿真结果比较

总结以上轮-雪交互模型，经验公式可以拟合雪的下陷量、压力和密度之间的关系，并由此计算轮胎、履带在雪面行驶时的阻力和牵引力，但由于雪的流变特性，不同时间、环境下的雪材料参数依然会有较大的变化；解析模型应用雪的材料属性模型，在轮-雪交互的变形作用下，通过对雪面的受力分析，可以得到轮胎的牵引力、行驶阻力解析值，但只能提取单一的性能参数；有限元模型可以结合轮胎行驶状态，研究不同纵向滑移、侧向滑移等情况下的应力分布，可以得到轮-雪交互作用下，车辆不同行驶工况下的车轮以及雪壤状态信息.

3 总结与展望

文中针对高纬度极寒地区的轮-雪交互作用，归纳了雪的力学特性，轮-雪交互作用的经验模型，解析模型和有限元模型的优缺点及其应用和改进方向.

未来对于轮-雪交互作用的研究需要结合极地雪壤硬度、厚度、密度、平均接地比压等物理特性,综合考虑内摩擦角和粘结力效应，建立极地车辆行走机构与雪面交互的数值计算模型，采用离散元法等方法模拟可变性积雪与行走机构动态交互作用下的雪颗粒行为，分析不同车速和典型极地雪壤环境下，基于轮-雪交互作用的行走机构构型的优化，综合提升极地车辆行走机构推进效率.