基于格陷门的高效密钥封装算法

谭高升, 张 锐 , 姜子铭 , 孙 硕

1中国科学院信息工程研究所 信息安全国家重点实验室 北京 中国 1000932中国科学院大学 网络空间安全学院 北京 中国 100049

1 引言

1.1 研究背景

密钥封装机制(Key Encapsulation Mechanism, KEM)是密码系统中重要的密码原语之一, 结合数据封装机制(Data Encapsulation Mechanism, DEM), 可以构造实用的公钥加密方案, 这种混合加密方式已经被国际标准化组织采纳为公钥加密标准[1], 广泛应用于互联网等通信系统。密钥封装方案还可以用来构造密钥交换协议、认证密钥交换协议[2-3], 为网络安全通信提供基础保障。传统密钥封装方案通常基于大整数分解问题或离散对数问题构造, 随着量子计算机研究的深入, 传统密钥封装方案将面临被彻底攻破的风险[4], 因此, 研究抵抗量子计算攻击的密钥封装方案已经成为密码学界关心的热点。

美国国家标准与技术研究院(NIST)于2017年开始向全球征集后量子公钥密码算法标准, 中国密码学会(Chinese Association for Cryptologic Research, CACR)于2018年末同样开展了密码算法设计竞赛活动, 并鼓励提供后量子密码算法。其中, 从提交算法的数量分析, 基于格的密钥封装算法是后量子密钥封装算法的主流算法。基于格的密钥封装算法具有抵抗已知量子攻击[4-5]、计算简单[5-8]、底层困难问题存在“最坏情形(Worst-Case)”到“平均情形(Average-Case)”的安全归约[6,9]等优势, 是后量子密钥封装算法中最具应用前景的基础算法。NIST和CACR均要求从算法设计、可证明安全分析、参数选取、攻击分析和高速实现等方面对提交算法进行全面设计与分析, 这是后量子算法设计的标准规范。据此设计完成的密钥封装算法为后量子算法标准化提供了重要的算法支持。

密钥封装方案作为基础的密码算法之一, 支持计算资源受限设备之间的安全通信同样重要。综合考虑后量子通信及计算资源受限设备等新型网络机密通信的需求, 本文的研究目标定位设计并实现高效的基于格的密钥封装算法。

1.2 相关工作

在IND-CCA安全的密钥封装算法构造中, 存在两种构造模型, 分别是标准模型和随机喻言机模型。标准模型下的方案可以避免随机喻言机实例化带来的安全隐患[10-11], 但通常效率较低, 无法满足实用性要求; 随机喻言机模型下的方案则结构简单, 算法效率高, 更容易满足实用性要求。

Micciancio与Peikert、Zhang等人分别利用BCHK变换[12]构造了基于格的IND-CCA安全的公钥加密(密钥封装)方案[13-14], 但方案效率较低, 在LWE (Learning With Error)假设[5]下, 达到近似128比特经典安全性, 参考文献[14]中统计的两种方案的密文长度分别为24.74KB与13.80KB, 不利于构造高效的IND-CCA安全的密钥封装方案。参考文献[15]利用有损陷门函数(Lossy Trapdoor Function)构造了标准模型下, 基于LWE假设的IND-CCA安全的公钥加密方案, 与文献[13]和[14]相比, 其方案密文长度更长, 算法效率更低, 更不利于构造高效的公钥加密方案。

为构造基于格的IND-CCA安全的高效密钥封装方案, NIST后量子标准化竞赛的候选算法均采用量子随机喻言机模型下的构造方式。遗憾的是, 在基于基础公钥加密方案(低安全性公钥加密)构造IND-CCA安全的密钥封装算法时, NIST提案都采用了非常相似的方式进行构造, 即利用量子随机喻言机模型下的Fujisaki-Okamoto (FO)变换[16], 将不同假设下的 Lindner-Peikert (LP)加密方案[17]转化为IND-CCA安全的密钥封装方案。

Naehrig等人[18]基于LWE假设构造密钥封装方案, 其基础公钥加密方案本质上是基于LWE的LP加密方案, 然后利用Hofheinz等人[19]提出的量子随机喻言机模型下的FO变换, 将基础公钥加密方案转化为IND-CCA 安全的密钥封装方案。基于LWE的密钥封装方案优势在于降低了因特殊环结构带来的安全风险, 因此安全性更高, 缺点在于公钥较大, 密文扩展因子(密文长度/明文长度)较大, 近似128比特经典安全性下, 密文长度为15.40KB, 不利于方案的实际应用。

为避免LWE假设带来的密文扩展问题, NIST后量子算法竞赛的大部分提案采用环结构进行方案构造。Poppelmann等人基于Ring-LWE (RLWE)假设[7]构造了满足IND-CCA安全性的密钥封装方案[20], 显著地解决了公钥长度、密文扩展因子较大的问题。Schwabe 等人对LWE和RLWE假设进行了折衷处理, 提出了基于Module-LWE (MLWE) 假设[8]的密钥封装方案[21], 方案既保留了RLWE类方案公钥和密文扩展因子较小的优势, 同时降低了环代数结构带来 的安全风险。Lu等人[22]结合纠错码, 构造了基于RLWE的密钥封装方案, 其方案可以使用非常小的模数(q=251), 显著压缩了公钥和密文长度。D’Anvers 等人基于RLWR (Ring Learning With Rounding)假设[23-24]构造了IND-CCA 安全的密钥封装方案[25], 部分解决了加密算法误差采样的问题, 但并未彻底解决, 其密钥封装方案依然需要部分误差采样。Chen与Bernstein等人分别提出了基于NTRU假设[26]的密钥封装方案[27-28]。Garcia-Morchon 等人[29]则基于RLWE 假设利用Reconciliation机制直接构造了密钥交换协议, 但并未达到CCA的安全性。在环结构下, 达到近似256比特经典安全性, 大部分方案的公钥在2KB左右, 基本满足实用要求。

虽然这些基于格的密钥封装方案在算法安全性和效率上均达到了较优的水平, 但是, 这些方案仍然存在一定的不足。首先, 在构造IND-CCA安全的密钥封装方案时, 需要对基础加密方案进行去随机化操作, 即将其转化为确定性加密。去随机化操作既增加了计算开销, 又增加了安全性证明中安全归约的复杂度(去随机化的哈希函数需要作为量子随机喻言机处理)[19,30]。其次, 加密和密钥封装算法均需要进行随机数和误差采样操作, 降低了算法效率且容易受到侧信道攻击。

显然, 如果基础公钥加密采用基于格的确定性公钥加密, 则加密算法不需要随机数采样和误差采样的操作, 这种基础加密方案更利于构造量子随机喻言机模型下, IND-CCA安全的高效密钥封装方案。但是, 目前基于格的确定性公钥加密方案效率较低[31]。一方面, 如果基于Gentry-Peikert-Vaikuntan- athan (GPV)陷门[32]构造基础加密方案, 则方案的密钥生成算法耗时很长, 难以大规模应用。另一方面, 如果基于Micciancio-Peikert (MP)陷门[13]构造基础方案, 则方案的公钥和密文较大, 同样无法满足应用需求。因此, 目前两种陷门均无法构造出高效的确定性公钥加密方案。

1.3 本文贡献

本文的主要贡献是基于优化的格上单向陷门函数, 构造了IND-CCA安全的高效密钥封装方案, 具体贡献如下:

(1) 针对密钥封装场景, 构造了高效的基于格的单向陷门函数, 从而构造了高效的确定性基础公钥加密方案。具体地, 当加密消息为比特或比特向量(多项式)时, 可以极大地压缩MP陷门, 从而显著地减小了基于MP陷门的确定性公钥加密的公钥、私钥和密文的长度。设RLWE (RLWR)假设中的模数为q, 则公钥、私钥和密文的长度比(压缩后长度/压缩前长度)分别为2/(logq+ 1)、1/logq和3/(logq+ 2), 当logq取较为常用的参数值13时, 公钥、私钥和密文的压缩率(1-长度比)分别为86%、92% 和80%。

(2) 基于优化的格上单向陷门函数和量子随机喻言机模型下的FO变换[30], 构造了IND-CCA安全的高效密钥封装方案。方案避免了去随机化、随机数生成、误差采样等操作, 提升了方案效率。

(3) 对方案进行攻击分析、参数设置分析以及软件实现。通过攻击分析, 在256比特经典安全性下, 密钥封装方案的公钥长度约为2KB。在Intel(R) Core(TM) i5-7200U CPU @ 2.50GHz 平台下, 达到256比特经典安全性, 密钥封装算法的运行时间仅为452 μs, 验证了密钥封装算法高效的预期。

1.4 技术原理

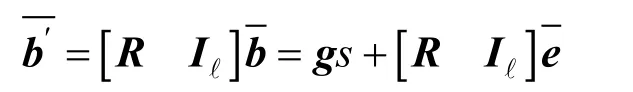
由于g特殊的结构形式, 当误差项的长度(二范数)“较小”时, 可以容易的利用最近平面算法[33]求出s。但是, 如果直接利用MP陷门, 校验多项式向量a的维数至少为log+1q维。由于a与公钥和密文直接相关, 当logq较大时, 导致方案的公钥和密文长度快速扩张, 无法满足实用要求。

值得注意的是, 密钥封装方案中, 基础加密方案的消息通常只取系数为二进制的多项式m∊R2, 并作为导出会话密钥的随机种子。我们发现, 此时的g向量只选取一项即可实现秘密信息的求解。基于这个观察, 可以对MP陷门进行显著压缩, 进一步, 实现了对校验多项式向量a的显著压缩。在第4章方案构造中, 可以看到R作为私钥只包含1个多项式,a作为公钥只包含2个多项式元素, 极大地减小了基于MP陷门的基础公钥加密方案的存储开销(自然降低计算开销), 为构造基于格的IND-CCA安全的高效密钥封装方案奠定了基础。基于RLWR假设构造的基础加密方案满足确定性OW-CPA安全性, 因此, 结合量子随机喻言机模型下的FO变换[30], 可以构造不需要去随机化、随机数采样和误差采样的IND-CCA安全的密钥封装方案, 使得方案效率更高、安全归约更简单。

由于基于RLWR假设的密钥封装方案对模数q要求更高, 因此, 在RLWR假设的模数q下, 很难使用Number Theorem Transform (NTT)计算模多项式乘法运算, 使得方案实现效率较低。本文为使用NTT进行快速计算, 首先在足够大的素数下使用NTT计算整数域上的多项式乘法, 计算结束后再通过模q运算将多项式的模数转化到RLWR模数下。这种实现方式显著提高了算法运行效率, 同时扩展了基于格的密码算法参数选取空间, 保证了算法的运行效率。

1.5 对比分析

与NIST征集的基于格的后量子密钥封装算法相比, 本文的密钥封装算法具有如下特点。

第一, 方案的设计具有创新性。由于基于格的单向陷门函数要么陷门生成算法较为耗时, 要么需要较大存储空间, 因此, 所有提案均未直接使用单向陷门函数作为基础原语, 构造IND-CCA安全的密钥封装方案或公钥加密方案。本方案首次对基于格的单向陷门函数进行了压缩优化, 并利用优化的单向陷门函数构造了高效的密钥封装方案, 丰富了基于格的密钥封装方案的构造方式, 从而可以满足更多应用场景的需求, 例如, 缺少计算资源进行误差分布采样的设备。

第二, 本方案的密钥封装(加密算法)算法不需要去随机化、误差采样、随机数采样等操作, 降低了对计算资源的要求, 减小了遭受侧信道攻击的风险。理论上, 更利于在资源受限设备上应用部署, 例如多种传感器网络、物联网等。

第三, 虽然方案的模数与多项式的次数不满足直接使用NTT的一般性条件要求(q≡ 1(mod2n)且q为素数,n为2的幂次, 模多项式为 1n X+ ), 但我们先在大模数下利用NTT计算多项式乘法, 得到多项式在整数域上的乘积, 再通过模运算将其转化为qZ上的多项式, 依然实现了使用NTT计算多项式乘法[34]。我们发现, 计算多项式乘法时大模数NTT与小模数NTT的实现效率十分接近。因此, 本文的实现方法可以扩展RLWE或RLWR假设[7,23-24,35]参数选取空间。

本文提出的算法不足之处在于密钥封装算法传递的随机种子空间受限, 只适用于分量为比特的向量(多项式)。其次, 由于RLWR假设的误差分布为上的均匀分布, 为保证方案的正确性,p的取值具有下界要求, 为保证RLWR的安全性,q与p的比值同样具有下界要求, 导致模数q比同等安全强度下RLWE假设模数大, 从而算法的公钥和密文长度较长。图1与图2分别为近似(AES) 128比特与(AES) 256比特(NTRU算法均为128比特, NTRUPrime算法最高为192比特)经典安全性下, 本文密钥封装算法与NIST二轮候选算法在公钥、密文长度和封装算法、解封装算法运行时间的对比图。

图1 128比特经典安全性下本算法与NIST二轮密钥封装(交换)算法性能对比Figure 1 The comparison of the performance on NIST round 2 candidates and ours in 128-Bit classical security

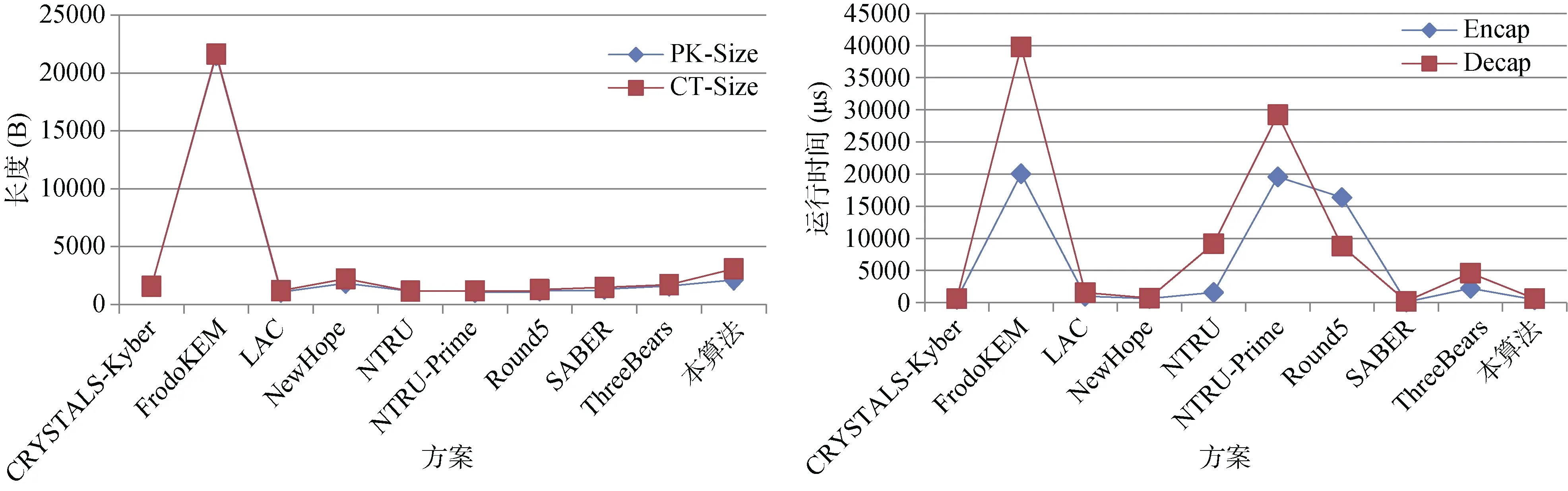
图2 256比特经典安全性下本算法与NIST二轮密钥封装(交换)算法性能对比(256比特)Figure 2 The comparison of the performance on NIST round 2 candidates and ours in 256-Bit classical security

如图1与图2中公钥长度与密文长度对比图所示, 除FrodoKME外, 其他NIST算法的密文长度和公钥长度较为接近。在128比特经典安全性下, 公钥长度与密文长度均约为1KB, 在256比特经典安全性下, 公钥长度和密文长度均约为2KB, 基本满足实用性要求。而FrodoKEM公钥和密文长度较长的原因是, 此算法基于LWE假设, 而其他算法基于环结构下的基本假设, 在存储和传输开销方面, 基于环结构的基本假设更具优势。由于本文算法的模数q取值较大, 相对而言, 本文算法的公钥长度与密文长度相对较大。其中, 相应安全强度下, 公钥长度约为1KB或2KB, 与NIST征集算法公钥长度近似, 而密文长度约为2KB或3KB。虽然在使用密文压缩算法下, 密文长度会减小, 但出于方案安全性考虑, 本文未对密文进行压缩。即使如此, 在当前终端设备存储能力和网络速度不断提高的环境下, 方案依然满足实用性要求, 模数较大是本算法获得算法效率提升的代价。

如图1与图2中封装算法与解封装算法运行时间对比图所示, 本文算法运行时间优势较为突出。本文在统一的实验环境(Intel (R) Core (TM) i5-7200U CPU @ 2.50GHz, 8GB RAM, Ubuntu 16.04 LTS, gcc 5.4.0, OpenSSL 1.1.1c)下, 测量了NIST二轮候选算法中基于格的密钥封装算法, 并选取“参考实现”进行测量。从图中可以看出, 无论128比特经典安全性还是256经典比特安全性, 提案算法的运行时间均为数百微秒, 且与运行平台无关。而对比的NIST方案有些则需要特定平台优化。我们相信, 针对特定平台, 本文方案效率还有提升空间。

2 预备知识

符号定义:

小写黑体字母表示向量, 例如a, 大写黑体字母表示矩阵, 例如A;

D-RLWE假设是指给定多项式个采样, 对任意多项式时间区分算法, 区分采样来自分布 ,,sqAχ还是上的均分分布是困难的, 即区分成功的概率是可忽略的。当sχ← 时, 称此为D-RLWE假设的Normal Form形式[17], 与标准假设下的D-RLWE假设具有相似的安全性, 由于后文均采用此种形式下的D-RLWE假设, , 本文统称为D-RLWE假设, 多项式s的次数称为RLWE假设的维数。

定义2 (S-RLWR假设) 设正整数pq﹤ , 给定构造分布As,p,q如下

类似地, S-RLWR 假设指给定多项式个取自分布 ,,spqA的采样, 对任意多项式时间算法, 求出s的概率是可忽略的。特别地, 对于S-RLWR假设, 当s←R2时, 假设同样成立[24]。

定义=3 (g-陷门) 设m和q为正整数, 令ℓ =「logq」, 且满足m﹥ℓ, 记g=(1,2,… , 2ℓ-1)T, 设h∊Rq是可逆元素,是a以h为标识的g-陷门, 如果R满足

陷门R的“质量”在文献[13]中由R的最大奇异值衡量, 本文将其放宽为 2|| ||R, 且 2|| ||R越小表示R质量越高, 后文取 1h= 。

定义4 (密钥封装方案) 密钥封装方案由三个多项式时间算法构成, 记作KEM=(KG, Encap, Decap), 设安全参数为λ、密文空间为C、会话密钥空间为K, 三个算法定义为:(pk,sk) ← KG(1λ), 概率性密钥生成算法, 输入安全参数λ, 输出一对公钥和私钥(pk,sk); (c,k) ←Encap(pk), 概率性封装算法, 输入公钥pk, 输出密文c∊C和会话密钥k∊K;k′← Decap(sk,c), 确定性解封装算法, 输入私钥sk和密文c, 输出会话密钥k′, 这里k′可以为⊥, 即允许解封装失败。

定义5 (KEM方案的IND-CCA安全性) 设安全参数为λ, 称KEM方案满足IND-CCA安全性, 如果对任意多项式时间敌手A, 如下定义的攻击优势满足

公钥加密方案同样由三个多项式时间算法构成, 记PKE=(KG, Enc, Dec), 设明文、密文空间分别为M与C, 则有(pk,sk) ← KG(1λ), 概率性密钥生成算法, 输入安全参数λ, 输出一对公钥、私钥(pk,sk);c←Enc(pk,m), 概率性或确定性加密算法, 输入公钥pk与消息m, 输出密文c;m′← Dec(sk,c), 确定性解密算法, 输入私钥sk和密文c, 输出消息m′。定义PKE方案解密失败的概率为

E表示求期望, 即此处定义了平均意义下, 解密失败的概率。在完美解密(Perfect Decryption)意义下, 方案解密失败的概率定义为对任意( , )pksk, 失败概率定义为。此处使用平均意义下的定义是因为, 本文构造的方案无法实现完美解密, 而在我们的安全性定义下, 使用平均意义下的定义即可。进一步, 参考文献[19, 30]亦采用平均意义下的定义, 为正确利用其中的相关结论, 本方案也必须采用平均意义下的定义。PKE满足选择明文攻击(Chosen Plaintext Attack, CPA)下单向安全性, 如果对任意概率多项式时间敌手A, 如下定义的攻击优势满足

进一步, 可以定义关于PKE的选择密文攻击下不可区分安全性(IND-CCA), 即对任意概率多项式时间敌手A, 如下定义的攻击优势满足

3 RLWE陷门优化

本节主要介绍如何利用MP陷门求解RLWE或RLWR问题, 并且, 针对特殊的秘密信息s, 实现对MP陷门的优化。RLWE与RLWR假设具有非常相似的结构形式, 唯一的区别在于两种假设下误差分布不同, 在MP陷门求解RLWE或RLWR问题中, 只有误差的长度对求解过程有影响, 而误差分布的形式对求解过程没有影响, 因此, 本节将以RLWE假设为目标, 分析RLWE问题的求解和陷门优化, 对于RLWR假设, 具有完全相同的求解和优化方法。

4 方案构造

本节基于RLWR假设, 首先构造满足OW-CPA安全性的公钥加密方案, 再利用QROM模型下的FO变换, 将OW-CPA的公钥加密方案转化为IND-CCA安全的密钥封装方案。在构造OW-CPA公钥加密方案时, 利用优化的g-陷门作为解密私钥, 加密算法中将明文消息作为RLWR假设的秘密消息, 而密文则是RLWR假设的样本实例。方案的优势在于, 加密算法不需要误差采样和随机数采样, 提高了加密算法的运行效率, 避免了采样带来的侧信道攻击风险。构造的IND-CCA安全的密钥封装方案自然地继承了这种优势, 从而同样提升了密钥封装算法的效率, 降低了遭受侧信道攻击的风险。同时, 由于OW-CPA方案又是确定性公钥加密方案, 避免了QROM模型下使用FO变换时去随机化操作, 减少了安全性证明中量子随机喻言机的个数, 降低了安全归约损失。

4.1 OW-CPA公钥加密

在构造g-陷门中特定结构的公开向量(矩阵)a时, 存在两种构造方式, 分别得到与(a中的分量1不包含在内)上的均匀分布统计或计算不可区分的公开向量, 在实际应用中, 采用计算不可区分就已经足够。同时, 满足计算不可区分的参数使得方案公钥、私钥和密文长度更小, 从而提高了加密方案的性能。本文采用计算意义下不可区分性, 并且通过RLWE假设保证公开向量a的计算不可区分性。假设方案的安全参数为λ, RLWE假设中误差分布为R上参数为σ的高斯分布, 即误差多项式的每个系数服从qZ上参数为σ的离散高斯分布, 记作χ。RLWR假设中,modq运算取值空间为基础加密方案的具体构造如图3。 根据近似取整得根据定理1的条件得

图3 OW-CPA公钥加密方案 Figure 3 Public key encryption with OW-CPA security

根据g-陷门恢复RLWR假设的秘密信息算法可知, 解密算法可正确输出明文信息。

定理2 (公钥加密方案安全性) 构造如图3所示的公钥加密方案, 假设在方案的参数设置下, D-RLWE假设与S-RLWR假设成立, 则构造的公钥加密方案满足OW-CPA安全性。特别地, 如果存在多项式时间敌手A攻破OW-CPA的公钥加密方案, 则可构造攻击D-RLWE假设的敌手B或攻击S-RLWR假设的敌手C, 敌手攻击优势之间满足

敌手B与C的运行时间与A的运行时间近似。

证明: 我们采用“游戏”跳转的方式对定理2进行证明。记事件表示在Gamei中敌手A返回挑战密文中加密的消息m。

定理证毕。

本文构造的OW-CPA公钥加密方案非常适合构造QROM模型下, IND-CCA安全的密钥封装方案。首先, 密钥封装方案的密文只用来传递导出会话密钥的随机种子, 通常为256比特或512比特的随机字符串, 满足高效OW-CPA加密方案对明文空间的要求。其次, 构造的OW-CPA方案加密算法既不需要随机数采样, 又不需要误差采样, 提高了加密算法效率的同时, 避免了去随机化操作。

4.2 IND-CCA密钥封装方案

本节主要利用QROM模型下的FO变换和OW-CPA安全的公钥加密方案构造IND-CCA安全的密钥封装方案。本文使用目前QROM模型下最优的FO变换[30], 可在降低通信开销的同时减小归约损失。本文构造的OW-CPA公钥加密方案其明文多项式即为RLWR假设下的秘密信息(多项式)。在RLWR假设中, 维数越高, 安全性越高, 维数越低, 安全性则越低。在密钥封装算法中, 本文将导出会话密钥的随机种子按位映射成明文多项式的系数, 例如, 随机种子为比特向量(an,…,a0), 则明文多项式为在实际方案中, 为节省随机比特, 随机种子的比特数通常小于RLWR的维数, 因此, 在实现中, 我们采用输出扩展函数(Extendable Output Function)对随机种子进行扩展, 补充缺失的高位系数。

设安全参数为λ, 记OW-CPA的公钥加密方案为PKE =(KG′,Enc′,Dec′), OW-CPA公钥加密方案的明文空间为M, 密文空间为C, 密钥封装方案的会话密钥空间为K, 哈希函数 :H×=→MCK是会话密钥导出函数。图4显示了QROM模型下, 基于确定性OW-CPA安全的公钥加密方案构造的IND-CCA安全的密钥封装方案。

图4构造的密钥封装方案与参考文献[30]中的KEM-V变换有两点不同。第一点, 文献[30]通过直接哈希随机种子的方式导出会话密钥, 本文将随机种子与密文一起哈希导出会话密钥, 由于方案是确定性加密, 所以本文的哈希方式不会增加会话密钥的随机性, 两种导出方式没有本质区别。第二点, 当解密出现错误时, 文献[30]利用伪随机函数将密文导出为会话密钥, 本文则利用哈希函数H将私钥中的随机串s与密文导出为会话密钥, 在安全性证明中H作为量子随机喻言机。这两种改变本质上与KEM-V构造是相同的, 可以将ss视为伪随机函数的密钥, 因此, 本文的两种改变不会对方案的安全性证明造成影响。

图4 IND-CCA密钥封装方案 Figure 4 Key encapsulation mechanism with IND-CCA security

根据密钥封装方案的构造方式, 易得密钥封装方案解封装失败的概率与OW-CPA安全的公钥加密方案解密失败的概率相同。密钥封装方案的安全性满足如下定理(与参考文献[30]的定理6类似)。

定理3 (密钥封装方案的安全性) 假设安全参数为λ, PKE满足确定性(量子) OW-CPA安全性, 且解密失败的概率为δ, 则图4构造的密钥封装方案在QROM模型下, 满足IND-CCA的安全性。具体地, 如果存在敌手A攻击密钥封装方案, 且A可以量子查询Eq次加密喻言机、量子查询Hq次随机喻言机H和经典查询Dq次解封装喻言机, 则可以构造敌手B攻击OW-CPA的公钥加密, 满足

B的运行时间与A的运行时间类似。

定理3的证明与文献[30]中定理6的证明非常类似, 这里不再赘述。利用图3构造的OW-CPA公钥加密方案作为密钥封装方案中的基础公钥加密方案, 即可得到高效的IND-CCA安全的密钥封装方案。进一步, 利用IND-CCA的密钥封装方案与IND-CCA的数据封装方案即可构造IND-CCA安全的公钥加密方案。这是构造IND-CCA安全的公钥加密方案的一种国际标准, 也是NIST后量子公钥加密算法标准竞赛中, 构造IND-CCA的公钥加密方案的通用方式。

5 实现与性能分析

本节对构造的IND-CCA安全的公钥加密方案进行实现并做性能分析。首先, 根据安全参数, 设置方案的所有参数, 包括D-RLWE假设的维数n、模数q、高斯分布的参数σ, S-RLWR假设维数n、模数p与模数q。其次, 需要对密钥封装方案中的哈希函数进行实例化, 并且为了节省随机比特, 设置合适的填充方式实现随机种子的填充。参数设置原则为保证方案正确性和安全性的前提下, 尽量采用小的参数, 从而提高方案的效率。注意, 在安全性分析中, 由于目前的安全性证明归约损失严重, 无法指导选取实用的安全参数。因此, 本文通过攻击分析的方式衡量参数的安全强度, 这也是国际上分析此类方案参数安全性的通用方法。

在参数设置时, 需要满足正确性和安全性要求。为了衡量密钥封装方案解封装失败的概率, 需要引入衡量高斯分布向量长度的引理1, 本文称为高斯分布向量尾部有界性引理(文献[36]引理4.3)。

其中,z的每个分量独立同分布于

由OW-CPA公钥加密方案的正确性定理(定理1), 只需密文的误差向量满足

本文利用Primal Attack攻击[37]与Dual Attack攻击对方案进行攻击分析, 当前, 这两种攻击是LWE类问题最优的攻击方式。分析所选参数下D-RLWE假设与S-RLWR假设的安全强度。在衡量BKZ算法[38]复杂度时, 经典模型下复杂度评估模型为b20.292b[39], 其中,b为BKZ算法Block的维数; 量子加速模型下复杂度评估模型为评估S-RLWR假设的安全性时, 将S-RLWR 假设中的误差分布视为上的均匀分布, 其标准差为。根据正确性和安全性的参数约束条件, 本文利用参数搜索脚本从多组参数空间中搜索出满足条件约束的较优参数。取多项式的次数n分别为512或1024, 记对应阶数下的密钥封装方案分别为KEM-512与KEM-1024, 搜索所得参数如表1。

表1 密钥封装方案参数选取Table 1 Parameters of key encapsulation mechanism

表1中“C-Sec”与“Q-Sec”分表表示攻击分析下, 方案参数可以达到的经典安全性与量子安全性。在正确性分析中, 分析始终保持方案解密失败的概率约为 2-140, 因此, 不同安全参数下解封装失败的概率均约为 2-140。通过引理1可以得到解密失败概率更小的参数, 但 2-140已经满足当前正确性和安全性的需求。在多项式次数取512和1024时, 分别选取了两组参数, 即pqł 与 |pq两种形式下的参数。其中, |pq的优势在于S-RLWR假设中的误差分布在这种情况下是无偏分布, 虽然, 目前不存在对有偏误差的攻击, 但是, 有偏误差分布可能会成为潜在的攻击目标, 因此, 本文提供两种形式下的参数设置。

与NIST后量子算法标准竞赛中的参数相比, 本文的模数q较大, 导致方案的公钥、私钥和密文相对较大。为了压缩公钥长度, 本文采用伪随机生成的方式生成公钥中的随机多项式, 即首先生成相应安全强度下的随机种子, 再利用伪随机函数对随机种子进行扩展, 扩展后的字符串转化为随机多项式的系数。在伪随机生成的方式下, 只需要存储和传输随机种子, 从而实现公钥长度压缩。KEM-512中随机种子为256比特随机字符串, KEM-1024中随机种子为512比特随机字符串。由于私钥多项式2r的每个分量取自 ,qσZD , 此时, 我们取采样区间为[5,5 ]σσ- , 这会极大地节省私钥的存储空间。导出会话密钥的随机种子seed在KEM-512与KEM-1024下分别取256比特随机字符串与512比特随机字符串。本文使用输出扩展函数 )(F∙对随机种子进行高位填充, 实际实现中使用CSHAKE哈希函数[41], 使得密钥封装中加密消息的长度达到512或1024比特。密钥封装方案公钥、私钥与密文长度计算公式分别为表示生成1a所用随机种子的长度,ssρ表示私钥中随机字符串ss的长度。

表2显示了IND-CCA安全的密钥封装方案的尺寸指标。目前, 近似256比特经典安全强度下, NIST后量子算法标准竞赛中, 基于理想格的二轮候选方案, 其公钥长度与密文长度均在2KB左右, 结合纠错码优化参数的方案公钥长度在1KB左右。虽然, 本文提出的密钥封装方案的存储效率未达到最优, 但是, 依然与NIST征集的二轮提案较为接近, 具体对比参见图2。

表2 密钥封装方案尺寸指标Table 2 The size of KEM

进一步, 本文对密钥封装方案进行了软件参考实现, 实验环境为Intel (R) Core (TM) i5-7200U CPU @ 2.50GHz, 8GB RAM, Ubuntu 16.04 LTS, gcc 5.4.0, OpenSSL 1.1.1c开源代码库, 所有算法的运行时间为1000次试验结果的平均值。表3为相应参数下, IND-CCA安全的密钥封装方案的运行时间。

表3 密钥封装方案算法运行时间Table 3 The performance of KEM

根据表3, 本文提出的密钥封装算法其软件参考实现性能达到较优水平。在近似128比特经典安全性下, 密钥生成算法、封装算法与解封装算法在普通 笔记本上的运行时间均在0.5ms以下。即使达到近似256比特经典安全性, 密钥封装算法每个算法的运行时间依旧保持在0.5ms左右。当前, 在NIST二轮候选方案中, 大部分方案的参考实现以及部分方案的优化实现, 也仅仅与本文算法参考实现效率相当。因此, 本文的密钥封装算法效率较高, 且本文算法的运行效率还具有进一步提升的空间。如果将本文算法的公钥和密文长度进行合理压缩, 加之本文算法计算简单, 不需要去随机化和误差采样, 算法效率高, 理论上更适用于于物联网等计算资源受限设备。

6 结论

本文利用优化的基于格的单向陷门函数, 构造了高效的IND-CCA安全的密钥封装(公钥加密)算法。首先, 针对密钥封装机制的构造场景, 优化了MP陷门, 压缩了陷门的长度。其次, 基于优化的陷门, 构造了基于RLWE与RLWR假设的确定性OW-CPA公钥加密方案, 方案的优势在于避免了去随机化、误差采样、随机数采样等复杂操作, 提高了方案的运行效率和实现安全性。进一步, 基于OW-CPA公钥加密方案构造了QROM模型下, 高效的IND-CCA安全的密钥封装方案。最后, 利用攻击分析的方法并结合方案正确性要求, 给出了方案的参数设置, 并对方案进行了软件参考实现, 在Intel (R) Core (TM) i5-7200U CPU @ 2.50GHz 8GB RAM的运行环境下, 算法的效率与国际最优水平相当, 从而验证了算法高效的特点。