长期荷载作用对内配工字型钢方钢管混凝土轴压短柱力学性能影响
2022-01-04赵萌萌史艳莉
赵萌萌, 史艳莉
(兰州理工大学 土木工程学院, 甘肃 兰州 730050)
钢管混凝土组合柱由于具有良好的承载力、抗震和抗火性能,已在工程中得到广泛应用.现阶段,超高层建筑及大跨桥梁等工程不断涌现,结构中的承重构件需有更好的承载能力和延性性能.内配型钢钢管混凝土柱不仅继承了钢管混凝土柱良好的受力特性,而且型钢对混凝土的包裹对其产生较强的紧箍力,在外荷载作用下能有效改善组合柱的承载力及延性,避免结构倒塌,从而使之具有更好的抗震性能,可作为结构中的重载柱.国内外诸多学者已对该种构件的基本力学性能、抗震及抗火性能进行了相关的试验和理论研究[1-6].但高层和超高层建筑服役过程中,构件承受长期持续的荷载作用,柱中混凝土将产生徐变变形,引起内力重分布、预应力损失、应力集中等现象.在同一层结构中构件的变形差异可能较小,但由于现代建筑层数较多,该种影响不断积累,将进一步影响整体结构的耐久性和适用性.因此有必要分析长期荷载对该类组合柱力学性能的影响.
目前,关于长期荷载作用下钢与混凝土组合构件的试验和理论研究主要针对钢管混凝土柱[7-15].在长期荷载作用下,由于核心混凝土所处的环境不同,内配型钢钢管混凝土组合柱具有更加复杂的工作机理,型钢和钢管均影响了混凝土的徐变特性,三个影响因素相互关联,相互耦合.而关于长期荷载对内配型钢钢管混凝土柱影响的研究较少.本次研究采用数值分析方法,利用ABAQUS对长期荷载作用下内配工字型钢方钢管混凝土轴压短柱的徐变变形、各组件的应力发展、接触应力等进行计算,并与不考虑长期荷载(即一次加载)的情况进行对比,分析长期荷载对该种组合柱的影响规律.并对影响长期荷载作用下该种组合柱变形和承载力的因素进行参数分析,研究变化规律,以期为工程实践提供参考.
1 有限元建模
1.1 模型建立
建立模型时钢管和型钢均采用二次塑流模型,一次加载时核心混凝土采用塑性损伤模型[7],具体表达式如下:
(1)
其中x=ε/ε0;y=σ/σ0;σ0=f′c,f′c为混凝土圆柱体抗压强度;ε0=εc+800ξ0.2×10-6;εc=(1 300+12.5f′c)×10-6;
考虑长期荷载作用时内配型钢钢管混凝土柱在不同阶段有不同的核心混凝土本构关系.在长期荷载作用阶段,采用黏弹性流变模型描述混凝土的徐变特性,利用ABAQUS提供的材料子程序UMAT定义长期荷载作用下混凝土的本构关系[15].在长期持荷后的再加载阶段,采用对一次加载的混凝土本构关系的修正模型描述混凝土的本构关系[7],即考虑徐变效应影响,保持应力坐标值不变,将εt= [1+φ(t,τ0)]ε0+εsh进行放大平移变化.
φ(t,τ0)为徐变系数,依据ACI209[16],计算公式为
(2)
其中:t-τ0为持荷天数;τ0为加载龄期;φmax(τ0)为徐变终值系数,取其值为0.9[17].
εsh为混凝土的收缩应变,计算公式为
(3)
其中,(εsh)max为干燥收缩终值,具体见文献[18].
考虑长期荷载作用与否的核心混凝土的应力-应变关系曲线对比如图1.

图1 核心混凝土应力-应变关系曲线[7]
模型中钢管和型钢采用8节点减缩积分三维实体单元(C3D8R).考虑大应变分析,核心混凝土采用8节点完全积分三维实体单元(C3D8).钢管、型钢与混凝土的界面接触采用面面接触,界面切线方向力的传递采用库伦摩擦模型,摩擦系数取0.25,法线方向采用硬接触.型钢、钢管和混凝土与加载板间的界面约束采用绑定.
考虑长期荷载作用的内配型钢钢管混凝土轴压柱模型的建立主要分为两部分:1) 采用力加载方式瞬时加载至NL(NL为施加的长期荷载值)并进行长期持荷,直至徐变结束,得出徐变变形计算结果.2)采用ABAQUS数据传递功能,将长期荷载作用下的组合柱模型作为初始状态导入新的模型中采用位移加载方式再加载,进行承载力等相关计算.建模时约束构件底端边界条件为U1=U2=U3=0,构件顶端边界条件为U1=U2=0.有限元模型建立和边界条件如图2所示.

图2 有限元模型示意图
1.2 模型验证
采用上述建模方式,首先利用文献 [1]中3个一次加载的内配型钢钢管混凝土轴压试件进行验证,计算其轴向荷载随轴向位移的变化曲线.试件信息见表1,试验结果和有限元计算结果见图3,可见二者吻合良好.由于未搜集到考虑长期荷载作用的内配型钢钢管混凝土轴压柱试验数据,因此对已有的考虑长期荷载作用的钢管混凝土轴压试验进行验证.验证主要包括两部分:长期荷载作用下的变形计算和考虑长期荷载作用时组合柱的承载力计算.图4a为长期荷载作用下试件的纵向应变随时间的变化曲线,图4b为考虑长期荷载作用的轴向荷载随轴向应变的变化曲线.图中B为钢管直径,ts为钢管厚度,L为试件长度,NL为施加的长期荷载值,t为持荷天数.图4c为考虑长期荷载作用时承载力验算结果,其中Nue和Nuc分别为试验值和计算值,可知两种结果吻合较好.因此,该建模方法合理可行,可用于考虑长期荷载作用的内配型钢钢管混凝土轴压柱力学性能分析.

表1 一次加载的轴压试件参数

图3 一次加载的轴压柱试验结果与有限元计算结果对比

图4 考虑长期荷载的轴压柱试验结果与有限元计算结果对比
2 受力全过程分析
考虑长期荷载作用的内配型钢钢管混凝土柱较钢管混凝土柱具有以下特点:
1) 核心混凝土的纵向徐变受到外部钢管和内置型钢的双重影响.
2) 在长期持荷阶段,混凝土的徐变使柱中各组件产生应力重分布,影响型钢的受力特性.
3) 在受力全过程中,型钢对混凝土产生横向约束,使之处于更加复杂的受力状态.
因此,采用上述建模方式,建立考虑长期荷载作用的内配工字型钢方钢管混凝土轴压短柱力学分析模型.基于设计规范和工程常用参数范围,取参数如下:钢管外边长B1=500 mm,钢管壁厚t1=11 mm,构件长度L=1 500 mm,钢管和型钢的屈服强度fty=fsy=345 MPa,混凝土立方体抗压强度fcu=60 MPa,钢管含钢率αst=0.1,型钢含钢率为αss=0.058,长期荷载比n=0.4,(n=NL/Nu,NL为长期荷载值;Nu为一次加载的计算承载力),加载龄期为28 d,持荷时间为 1 000 d.构件截面形式如图5所示.

图5 截面示意图
为分析内置工字型钢对考虑长期荷载作用的组合柱力学性能的影响,同时建立材料和截面尺寸相同的钢管混凝土轴压柱模型.
2.1 应变-时间分析
图6为长期持荷阶段钢管混凝土柱和内配型钢钢管混凝土柱的纵向应变(ε)-时间(t)曲线.由于混凝土的徐变作用,二者应变初期增长较快,之后增长速率逐渐降低,曲线趋于平缓.但内配型钢钢管混凝土柱应变增长稳定的时间略早于钢管混凝土柱.经计算,钢管混凝土柱开始进行长期持荷时的初始应变为616.05με,内配型钢钢管混凝土柱的初始应变为637.6με,大于钢管混凝土柱的初始应变.这是由于相同长期荷载比下内配型钢钢管混凝土柱施加的长期荷载值大于钢管混凝土柱.钢管混凝土柱1 000 d的应变终值为867.5με,应变增长率为40.8%,加入型钢后1 000 d的应变终值为828.5με,应变增长率为29.9%,小于钢管混凝土柱,即加入型钢可有效减弱长期荷载对钢管混凝土柱应变的影响.主要原因是长期持荷阶段型钢对混凝土产生了横向约束力,影响其纵向变形.

图6 长期持荷阶段ε-t关系对比曲线
2.2 荷载-应变分析
图7为两种轴压短柱的荷载(N)-应变(ε)全过程曲线.实线表示考虑长期荷载的情况,虚线表示一次加载的情况.长期荷载使内配型钢钢管混凝土柱的极限承载力提高1.4%,对应的应变增大81.4%.对于内配型钢钢管混凝土组合柱,长期荷载分别使其极限承载力和对应的应变增大1.8%和78.0%.

图7 全过程N-ε曲线
由上述分析可知,长期荷载对内配型钢钢管混凝土柱的影响与钢管混凝土柱有所区别.因此,有必要对考虑长期荷载影响的内配型钢钢管混凝土轴压柱工作机理进行深入研究.
2.3 破坏模态分析
图8为考虑长期荷载作用与否内配型钢钢管混凝土轴压短柱的破坏模态.长期持荷后对构件再加载,其破坏模态和一次加载时类似,均表现为钢管外表面出现若干屈曲.图9为考虑长期荷载作用与否内配型钢钢管混凝土轴压短柱中截面破坏模态,和一次加载的情况类似,由于方钢管的不均匀约束,再加载后钢管和混凝土在四个角部区域接触良好,其他区域明显脱开,混凝土和型钢上下翼缘处脱开.

图8 构件整体破坏模态

图9 柱中截面破坏模态
2.4 跨中截面应力分析
2.4.1核心混凝土
图10为考虑长期荷载时跨中截面核心混凝土的纵向应力随纵向应变的变化曲线.由于混凝土各处应力发展不均匀,取图5中的1点、2点、3点和4点分析.在长期持荷阶段,由于混凝土的徐变导致其应力松弛,各点应力线性减小.长期荷载作用结束后四个特征点的应力不断强化,位于边长中部的3点和1点混凝土横向变形较大,最先达到应力峰值.随着纵向应变进一步增加,应力值开始减小.4点位于钢管角部角点处,在轴压荷载下由于此处较强的约束作用,应力强化至1.17f′c(f′c表示混凝土圆柱体抗压强度),之后由于角部作用加速混凝土微裂缝的发展,因此应力逐渐下降.2点位于型钢内包区域,型钢对该处混凝土形成较强的横向约束,可有效延缓混凝土微裂缝的发展,应力最大达到1.28f′c,下降缓慢.

图10 考虑长期荷载时核心混凝土σ-ε曲线
图11为考虑长期荷载与否轴压柱达到极限承载力时跨中截面核心混凝土的纵向应力云图.可知,长期荷载使受到约束较强的钢管角部附近和型钢包裹区域的混凝土应力值提高,而其他区域应力减弱.

图11 核心混凝土纵向应力云图
2.4.2外部钢管
图12为考虑长期荷载与否跨中截面钢管的Mises应力、纵向应力和横向应力曲线.取受轴压荷载时环向鼓曲较大的3点处(见图5)进行分析.考虑长期荷载时,在加载初期和长期持荷阶段,纵向应力和Mises应力迅速增大,此时横向应力缓慢增长,钢管横向受拉.当应变达到2 715.39με时,钢管Mises应力达到345 MPa,纵向应力不断减小,横向应力逐渐增大并在持荷后期保持稳定.一次加载时此处钢管在应变达到3 463.54με时钢材才进入屈服,即长期荷载使得钢管达到屈服应力提前21.6%.说明长期荷载作用加速了钢材的塑性发展,这是由于长期持荷阶段钢管承担了混凝土卸下的部分荷载,导致其应力增大.由于长期荷载作用的影响,钢管的纵向应力峰值有所增大,且对应的应变有所增加.另外,长期荷载使钢管开始强化的时间延后且延缓了横向应力的发展.
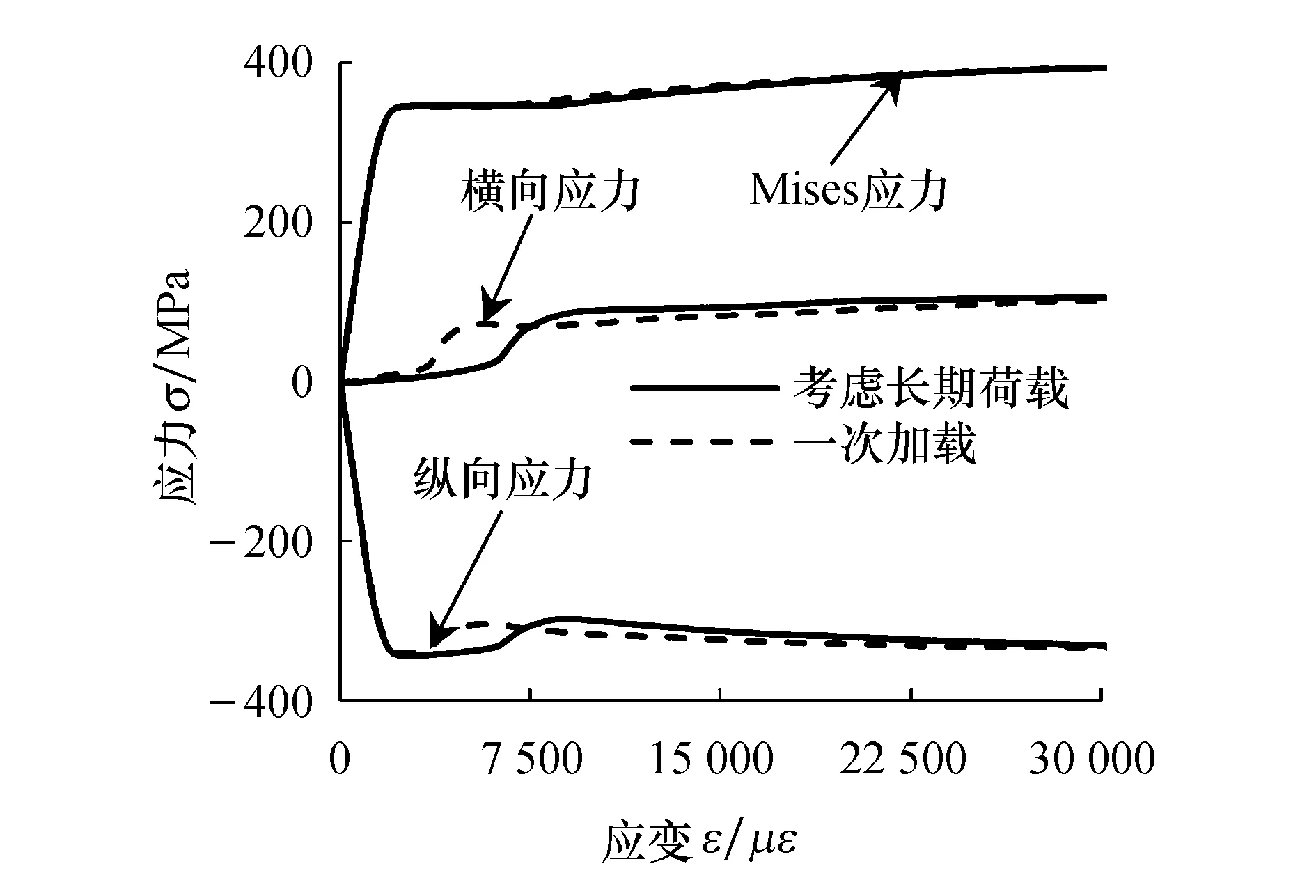
图12 钢管σ-ε曲线对比
2.4.3内部型钢
图13为考虑长期荷载与否跨中截面型钢的纵向应力-应变曲线.取图5中的2点、5点和6点进行分析.无论考虑长期荷载作用与否,型钢3个点应力发展基本一致,即随应变的增长纵向应力迅速增大,随后3个点应力几乎同时达到峰值,之后逐渐下降,进入强化阶段.但腹板中部2点处型钢塑性下降段更为明显.对比一次加载的情况可知,长期荷载作用使得3个特征点处的应力峰值有所提高,且达到峰值的时刻有所延后,但对2点处的提高幅度大于5点和6点.

图13 型钢纵向应力曲线对比
图14为考虑长期荷载作用时型钢3个特征点处的Mises应力曲线.可知三个点应力同时达到345 MPa,但进入强度阶段的时刻略有区别,腹板中部的2点最先开始强化,且应力强化程度最高.

图14 考虑长期荷载时型钢Mises应力曲线
图15为长期荷载对型钢特征点Mises应力曲线的影响规律.可知长期荷载对3个点的影响与外钢管基本一致.即考虑长期荷载作用时型钢的Mises应力达到屈服时刻早于不考虑长期荷载的情况,这是由于在长期持荷阶段柱中各组件发生应力重分布,型钢承担了混凝土卸下的部分荷载,加速了型钢的屈服.并且,长期荷载使得型钢强化开始的时间有所延迟.

图15 型钢Mises应力曲线对比
图16为长期荷载对型钢横向应力-应变曲线的影响规律.可知,3个点的横向应力发展规律较为一致,但2点的横向应力值远大于5点和6点.与一次加载的情况相比,长期荷载作用使得横向应力大幅增长的时刻有所延迟.
2.5 接触应力分析
2.5.1钢管与混凝土间的接触应力
图17为考虑长期荷载与否跨中截面钢管与混凝土的接触应力(p)-应变(ε)曲线.图中εm表示考虑长期荷载时轴压柱达到极限承载力时对应的应变,εm,not表示一次加载时轴压柱达到极限承载力时对应的应变.由于方钢管的不均匀约束,钢管在角部角点处对混凝土的约束力最大,随着离角点距离的增大约束力迅速减小,中部接触应力为0 MPa.无论是否考虑长期荷载作用,均在应变发展一定阶段后二者才产生接触应力,但长期荷载作用延缓了接触应力出现的时间.原因是在长期持荷阶段,钢管环向受拉,由于泊松比大于混凝土,二者脱开.长期荷载结束后,混凝土膨胀加快,二者开始产生接触应力.对比一次加载的情况,长期荷载作用使接触应力峰值有所增大;达到峰值应力时对应的应变也有所增大;当轴压柱达到极限承载力时,长期荷载所对应的接触应力大于一次加载的情况.

图17 跨中截面钢管与混凝土间p-ε曲线
图18为两种情况下不同高度处钢管角点和混凝土的接触应力曲线.可知二者接触应力在跨中最大,沿短柱两端逐渐减小.在长期持荷阶段,三个截面均无接触应力存在,长期持荷结束后,随着应力不断增加,混凝土膨胀变形加快,中截面首先产生接触应力,随后接触应力不断向柱端传递.长期荷载对三个截面处二者的接触应力影响规律与中截面一致.
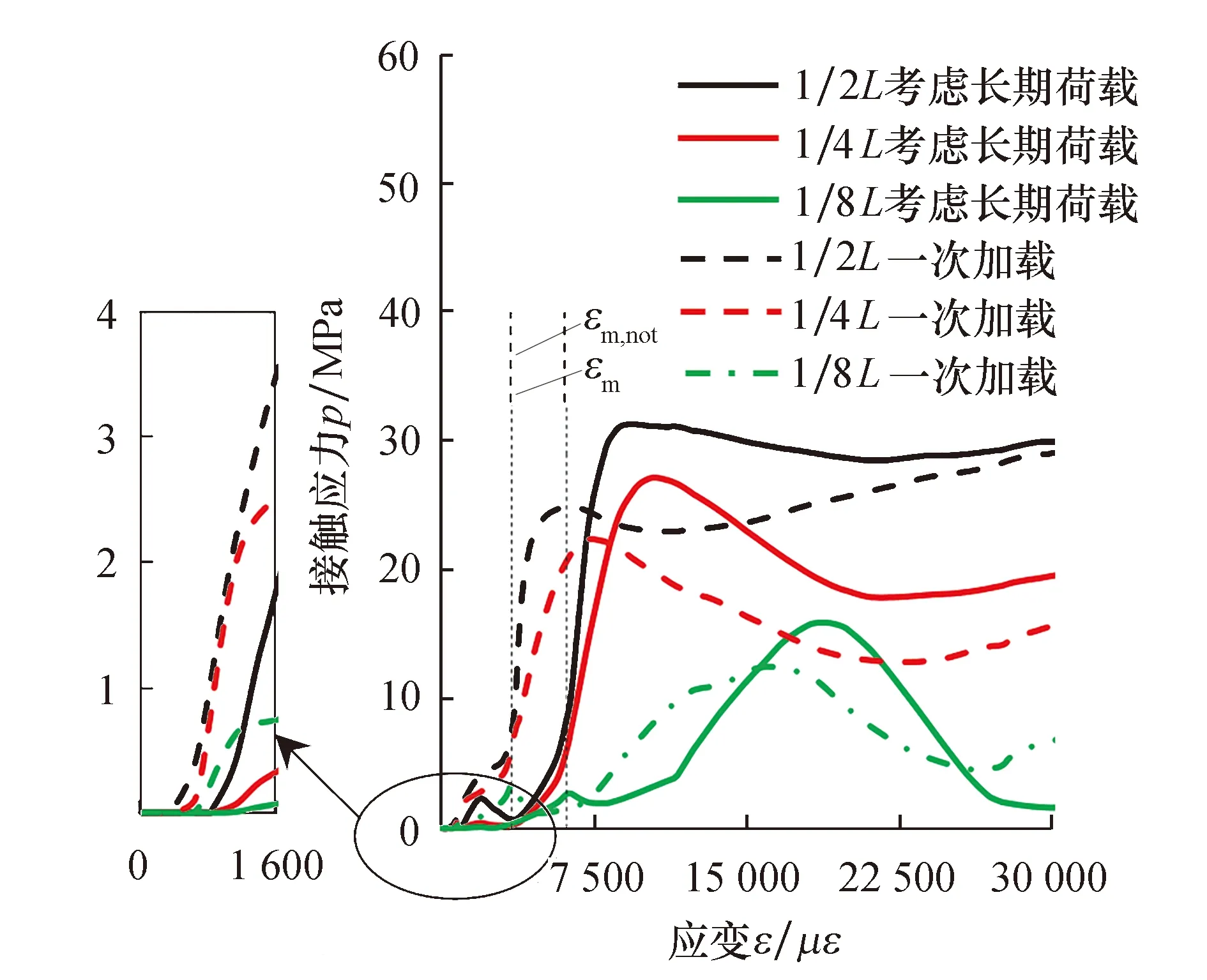
图18 不同高度钢管与混凝土间p-ε曲线
2.5.2型钢与混凝土间的接触应力
图19为长期持荷时中截面特征点处型钢与混凝土的接触应力(p)-时间(t)曲线.与钢管和混凝土的接触应力不同,在受力初期型钢翼缘上表面6点处与混凝土存在接触应力,腹板内侧的5点,中部2点与混凝土脱开,二者接触应力为0.说明在受力初期,二者的接触应力主要分布在翼缘外表面.在长期持荷过程中,由于混凝土的徐变作用,截面内混凝土应力松弛,二者接触应力随时间增长不断减小.

图19 长期荷载作用下中截面型钢与混凝土p-t曲线
图20为两种情况下跨中截面型钢与混凝土的接触应力(p)-应变(ε)曲线.可知型钢与混凝土的接触应力小于钢管与混凝土的接触应力.对于考虑长期荷载的情况,长期持荷结束后5点和2点接触应力逐渐超过6点,即随着应变的不断增长,型钢对包裹区域的核心混凝土产生的约束力强于型钢外侧.较一次加载而言,长期荷载对3个点的接触应力影响规律一致:延缓了型钢与混凝土接触应力出现的时间;使接触应力的峰值有所增大,达到峰值应力时对应的应变有所增大;当轴压柱达到极限承载力时,接触应力有所增强.这也解释了上述长期荷载使型钢包裹区域混凝土应力增大的原因.

图20 跨中截面型钢与混凝土间p-ε全过程曲线
3 参数分析
由上述分析可知,长期荷载影响了内配工字型钢方钢管混凝土轴压短柱的变形和承载力.为进一步分析不同参数对长期荷载作用下组合柱徐变变形和承载力的影响规律,定义徐变系数φt和承载力影响系数kp如下:
式中:εt为长期持荷1 000天时轴压柱的纵向应变;εi为开始进行长期持荷时的初始应变.NuL为考虑长期荷载时组合柱的极限承载力,Nuo为一次加载时组合柱的极限承载力.
图21和图22分别为长期荷载对徐变系数和承载力影响系数的影响规律.

图21 长期荷载对徐变系数的影响

图22 长期荷载对承载力影响系数的影响
3.1 长期荷载比
由图21可知徐变系数不随长期荷载比的改变而改变,这体现了长期荷载作用下混凝土线性徐变的特性.由图22可知,随着长期荷载比的增长,承载力影响系数变化较小.
3.2 混凝土强度
由图21可知,随着混凝土强度的增长,徐变系数逐渐增大,即混凝土强度提高使长期荷载作用下构件纵向应变增长更加显著.混凝土强度为90 MPa时的徐变系数较30 MPa时增加11%.由图22可知,随着混凝土强度提高,承载力影响系数也不断增大.即混凝土强度提高使得长期荷载作用对组合构件承载力的影响更加显著。当混凝土强度为90 MPa时,长期荷载使承载力提高2.5%.
3.3 钢管含钢率
由图21可知,随着钢管含钢率的增长,徐变系数不断减小.这是因为随着钢管含钢率的增大,核心混凝土的面积相对减小,其徐变减弱.由图22可知,承载力影响系数随着钢管含钢率的增大逐渐减小.钢管含钢率αst=0.05的承载力系数较αst=0.20时增大1.6%.
3.4 型钢含钢率
由图21可知,随着型钢含钢率的增长,徐变系数不断减小,原因与钢管含钢率的影响一致.由图22可知,承载力影响系数随着钢管含钢率的增大逐渐减小.型钢含钢率αss=0.04的承载力影响系数较αss=0.10时增大1.2%.
4 结论
通过数值模拟分析长期荷载作用对内配工字型钢方钢管混凝土轴压短柱力学性能的影响规律,得出以下结论:
1) 相同长期荷载比下内配型钢钢管混凝土柱变形增长稳定的时间较钢管混凝土柱有所提前,配置型钢可有效减弱混凝土徐变带来的应变增长.
2) 对受到紧箍作用较强的钢管角部附近和型钢包裹区域的混凝土,长期荷载使其纵向应力较一次加载的情况增大,使其他区域的混凝土应力降低.
3) 长期荷载作用使钢管和型钢提前进入屈服,但使二者的纵向应力提高,对应的应变增大并延缓横向应力的发展.长期荷载对钢管、型钢与混凝土间的接触应力影响规律较为一致,即延缓接触应力的发展;当组合构件达到极限承载力时,长期荷载作用使接触应力较一次加载时有所增强.
4) 由参数分析可知:长期荷载比的增长对徐变系数和承载力影响系数影响不大;混凝土强度增长使徐变系数和承载力影响系数增大;钢管含钢率和型钢含钢率增大使二者不断减小.
