桥面板徐变对曲线组合梁桥剪力钉受力性能的影响

冯军, 郭增伟*, 赵付强

(1.重庆交通大学土木工程学院, 重庆 400074; 2.中交路桥建设有限公司, 北京 100027)

钢-混凝土组合梁桥是由钢材和混凝土板通过剪力键连接而成的轻型结构，充分发挥了混凝土的抗压性能和钢材的受拉性能[1]，具有良好的受力特性，应用广泛。钢-混组合梁桥中混凝土板的徐变会使钢-混结合面之间产生相互作用力，不仅导致明显的内力重分布，还会产生一定的相对滑移[2]。众多学者对钢-混组合梁徐变效应开展了广泛的研究，刘沐宇等[3]开展钢-混组合梁混凝土桥面板的徐变试验，研究了港珠澳大桥钢-混组合连续梁桥超长时间下的收缩徐变效应，研究表明桥面板的收缩徐变对钢梁拉应力影响较小，而钢梁压应力增大显著，对混凝土板拉、压应力均有卸载作用且影响持续时间较长；冯联武等[4]以某双层钢桁架桥为背景，采用梁格法模拟钢-混组合桥面系，通过调整混凝土弹性模量以考虑徐变系数的时变特性，进而研究了徐变内力的空间分布，结果表明徐变造成结构受力较大的跨中、墩顶截面附近的桥面板上、下层有明显的应力差异，而其他部位桥面板应力上、下层之间差异不大；赵军等[5]针对大跨混凝土结构施工期间的安全问题，对比了施工期间是否考虑收缩徐变影响下结构内力的变化，结果表明在收缩徐变影响下结构的竖向位移会显著增加，并且剪力值和弯矩值均会有较大程度的增加；樊健生等[6]建立了考虑混凝土徐变的钢-混组合梁长期受力性能模型，利用逐步法计算组合梁截面内力和变形并与试验结果进行了对比，重点探讨了梁体挠度随时间的发展规律，结果表明现有规范对瞬时挠度及正弯矩区挠度的计算较为精确，负弯矩区挠度计算则需要考虑混凝土开裂的影响。

目前对于钢-混组合梁桥徐变研究多集中在桥面板、钢梁的内力和应力等方面，或梁体变形如桥梁挠度方面。实际上，作为重要连接构件的剪力钉在混凝土徐变影响下受力情况有较大变化，值得进一步研究。为探究这种变化，现以某钢-混组合曲线梁桥为背景，采用ANSYS建立包含剪力钉在内的精细化实体有限元模型，分析混凝土徐变影响下剪力钉内力及滑移变化情况，讨论预制板加载龄期、时间历程对剪力钉徐变内力的影响。

1 有限元模拟方法及正确性验证

1.1 ANSYS徐变模拟方法

混凝土徐变影响因素众多，作用机理相当复杂，徐变分析方法和理论模型较多，不同理论推导的徐变系数方程有所差异，为提高精度，需根据工程实际情况并结合混凝土试验确定其实际参数[7]。目前对于有限元中徐变研究主要集中在徐变机理的理论研究、徐变方程的推导及参数修正等方面[8-10]，较少涉及徐变计算理论在商用有限元软件中的实现，本文中侧重阐述徐变理论计算后的徐变系数在ANSYS中的应用。

金属蠕变与混凝土徐变存在相似性，ANSYS中通过金属蠕变Creep准则模拟混凝土徐变[11]，将理论推导及试验所确定的徐变系数作为金属蠕变方程的参数，而后调用该方程以金属蠕变形式考虑混凝土徐变效应。ANSYS中内置多个金属蠕变方程，选取6号方程，t时刻蠕变，即

(1)

式(1)中：σ为混凝土应力；T为环境温度；С1、С2、С3、С4为与各因素有关的常系数。

对式(1)中时间t求导得到徐变速率方程为

(2)

为使其正确模拟混凝土的徐变历程，以下对其进行参数的修正。线性徐变理论认为，徐变速率与混凝土的应力成一次线性关系，故可取式(1)中的С2=1。混凝土徐变是渐进发展的过程，本文中采用应变强化准则，即认为徐变速率取决于材料中的应变量С3取1。温度对徐变的影响较为复杂，为简化分析，暂不考虑温度影响，故С4取0，最终得到其徐变应变速率方程为

ε′=С1σ

(3)

(4)

式中：E为混凝土的弹性模量；φ为t时刻徐变系数。

而混凝土徐变应变速率一般表达式为式(4)，联合式(3)，最终可解得徐变方程参数С为

(5)

由式(5)可知，ANSYS中徐变模拟本质是根据不同时刻下材料的徐变系数φi(可根据JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[12]计算得出)求出徐变方程参数C1，将其赋值给内置的金属蠕变方程，从而实现徐变的模拟。此外，为保证真实反映混凝土的徐变变形，徐变模型需要考虑混凝土徐变系数随时间的变化。

ANSYS中对于材料徐变特性的模拟是改变不同时间步长内的材料系数，即每个时间步长内认为材料的徐变发展速率是相同的；故为保证准确性，在徐变发展较为迅速的早期，应将时间步长划分较短，而徐变后期为保证计算效率可适当加长。

综上，徐变龄期是混凝土徐变计算的关键，本桥中桥面板为预制混凝土板，在养护期间即会存在徐变变形，但此时板件处于无约束状态，变形自由，内部不存在由徐变引起的应力。在架设后，混凝土板与钢主梁通过现浇湿接缝连接为整体，混凝土板的徐变变形受到钢主梁约束，在结构内部产生徐变内力。在ANSYS中预制期间的徐变变形通过徐变龄期将其消除，即徐变龄期以架设时的混凝土龄期为准，在此之前的自由徐变不进行考虑。现浇湿接缝龄期较短，徐变发展较为剧烈，考虑到混凝土硬化需要一定的时间，其徐变龄期以3 d进行考虑。

1.2 ANSYS模型及剪力钉模拟方法

工程背景为5 m×30 m的某等截面钢-混组合曲线连续梁桥，全桥位于圆曲线上，半径R=400 m，全桥宽度为11 m。主梁采用双工字型钢板组合梁，主梁高1.55 m，中心间距为5.8 m；为满足强度和稳定性的要求，主梁内侧每隔5 m设置1道横隔梁，主梁腹板每隔2.5 m设置1道竖向加劲肋，外侧设置挑臂。上部采用存放龄期为90 d的预制钢筋混凝土板，桥面板之间通过浇筑横向、纵向湿接缝连接成整体。剪力钉采用圆柱头焊钉，直径为22 mm，采取均布式布置方式焊接在主梁、横梁上，通过湿接缝与预制混凝土板相连，实现结构整体受力。主梁采用工字型钢梁，而钢材存在蠕变特性，但考虑到金属蠕变的条件为高温和应力状态，而桥位温度显然不满足金属蠕变所需的高温状态，故不考虑钢梁的蠕变行为。预制桥面板为C50混凝土，湿接缝则采用С50微膨胀混凝土，以增强整体性；主梁、横梁、挑臂等均采用Q345低合金钢。施工时，从跨中向两边对称浇筑，最后通过浇筑支点处接缝，使全桥形成整体，桥梁的横断面如图1所示。

剪力钉是钢-混组合梁桥中传递荷载的构件，其模拟正确与否会显著影响结果的正确性。本文中使用ANSYS建立有限元模型，剪力钉采用COMBIN39单元模拟，为精确模拟钢梁与桥面板之间的滑移量，将COMBIN39单元的节点直接建立在钢板上缘和混凝土板下缘，此时2个节点位移的相对改变量即为剪力钉在实际情况下的滑移量。考虑到COMBIN39单元仅能模拟单一方向受力状态，而剪力钉的变形并非单向的，故在每个剪力钉位置布置2个COMBIN39单元，分别用于模拟剪力钉顺桥向、横桥向的受力及变形。

定义COMBIN39单元需要在有限元模型中确定其荷载-位移关系式，以确定其抗剪刚度，而对于其荷载-位移关系并无单一公式可表达，目前主要通过剪力钉抗剪试验归纳其回归函数，确定其具体表达式[13]；结合本桥剪力钉实际情况，选用Ollgaard等提出的荷载-位移关系式[14]，即

Q=Qu(1-e0.7Δ)0.4

(6)

式(6)中：Δ表示滑移量，mm；Q表示剪力钉剪力值，kN；Qu表示剪力钉抗剪承载力设计值，kN，根据《钢结构设计规范》(GB 50017—2017)[15]中对于剪力钉抗剪承载力设计值的相关规定，计算得其抗剪承载力设计值为60.1 kN。

全桥模型采用柱坐标系建立，以圆曲线圆心为坐标原点，X向为横桥向，Y向为顺桥向，Z向为竖向。混凝土桥面板采用SOLID65实体单元模拟，钢筋通过实常数进行定义，亦不考虑钢筋蠕变；钢主梁、横隔梁和加劲肋采用SHELL43单元模拟；根据剪力钉节点设置可知，钢主梁与桥面板之间存在一定的间隙，最初剪力钉和桥面板处于“杀死”状态，在同时激活剪力钉和桥面板后，两者通过剪力钉连接，桥面板受到钢主梁的约束，实现施工状态的转变。对于连续梁桥，固定支座应置于中跨，故约束2～3跨支点处钢横梁底部节点的DX、DY、DZ；其余支点处钢横梁底部节点则仅约束DX、DZ。全桥采用映射网格划分，共计613 461个节点，491 878个单元，其中X向及Y向剪力钉单元数均为15 636。考虑到施工阶段会对剪力钉的内力有较大影响[16]，采用“单元生死”功能模拟施工阶段，具体施工顺序为：①钢梁一次落架；②安装预制桥面板；③浇筑纵、横向湿接缝；④施加二期恒载。鉴于每跨布置相同，给出单跨钢梁有限元模型网格划分如图2所示。

图1 桥梁标准横断面图Fig.1 Bridge standard cross-section diagram

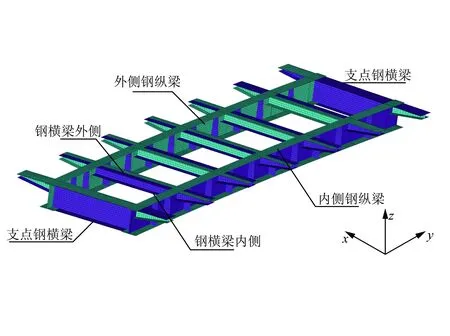
图2 单跨钢梁有限元模型及网格划分图Fig.2 Single-span steel beam finite element model meshing diagram

1.3 ANSYS徐变模拟的正确性验证

为验证上述混凝土徐变模拟的正确性，选取文献[17]中的两端固支的单跨超静定梁进行验证。该梁跨径18 m，截面为1.0 m×1.0 m的矩形，采用C50混凝土，自重以均布荷载形式施加，大小为1 kN/m。其施工顺序：先吊装固定两侧悬臂梁，而后浇筑C部位合龙单元，形成超静定结构，A梁与B梁的徐变龄期分别为190、5 d，算例结构如图3所示。

使用ANSYS建立有限元模型，主梁采用BEAM23单元模拟，全梁共99个节点，划分为98个单元，并通过“单元生死”功能模拟施工阶段，具体过程：激活A、B梁，并约束固定端节点位移并施加均布荷载，模拟“悬臂阶段”，而后激活合龙单元C并进行求解。按徐变参数计算公式(5)，分别计算A梁、B梁的徐变参数，并据此修改模型材料参数分步求解结构的徐变效应，2 000 d后不同关键截面的徐变弯矩值如表1所示,并与文献[17]中按Trost力法计算得到的理论值进行对比。

由表1看出，ANSYS计算得到的控制截面徐变弯矩值与经典算法Trost力法理论值最大相对误差仅为3.2%，说明了上述徐变模拟方法的可行性。值得注意的是，为便于Trost力法理论计算，悬臂梁中不考虑钢筋且下部不存在支撑，故其内力及边界条件与实际桥面板存在较大差异，由于内部应力状态对混凝土徐变特性有显著的影响，这可能导致两者徐变特性有一定的差异，但从徐变方程可以看出应力差异的问题可以较好地考虑在内。

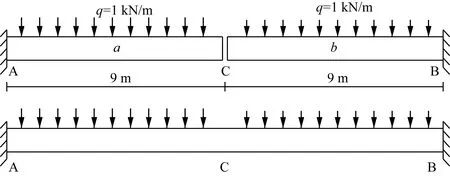
图3 算例结构示意图Fig.3 Schematic diagram of the example structure

表1 Trost力法理论值与ANSYS计算值对比Table 1 Comparison of the theoretical value of Trost force method and the calculated value of ANSYS

2 剪力钉徐变内力及滑移位移的空间分布

本桥桥面板预制龄期为90 d，本节对该龄期桥面板徐变影响下的剪力钉特性进行分析。不同于车辆荷载的“瞬时”作用，混凝土板徐变对剪力钉的影响是缓慢且持续性较长的过程，为直观表现这种影响，以成桥10年后剪力钉的徐变内力和滑移位移为例讨论其空间分布。下文中用到的剪力钉徐变效应T的计算方法为

T=Sj-Si

(7)

式(7)中：T表示徐变效应值(剪力钉内力、滑移)；Sj和Si分别为成桥j、i某时刻剪力钉内力、滑移量。

2.1 剪力钉内力变化的空间分布分析

2.1.1 钢纵梁剪力钉沿顺桥向的内力变化规律

在桥梁顺桥方向上，分别提取外、内钢纵梁成桥初期及成桥10年时剪力钉沿顺桥向、横桥向内力，按照式(7)绘制徐变内力分布图(图4、图5)。值得注意的是，COMBIN39单元内力是有方向的，若单元力为正，表示单元受到沿整体坐标系“向外”的剪力作用，反之相反；故若以剪力增量表现其受力特性时，为正表示剪力钉在徐变影响下，受到沿整体坐标系“向外”的作用，反之“向内”。

由图4、图5看出，外、内侧钢纵梁剪力钉在横桥向与顺桥向的内力均呈现出关于跨中“反对称”的分布规律，且由每跨跨中向两侧支点逐渐增大，且极值多出现在支点湿接缝附近，这是由于支点处采用现浇混凝土加载龄期短造成的，可采取加密布置剪力钉的方式降低单钉的徐变内力。此外，对比剪力钉在顺桥向与横桥向的徐变内力值，可以看出剪力钉在横桥向的徐变内力极值大约是顺桥向内力的2.0倍，在桥梁中徐变会导致梁体产生纵桥向的下挠，而在钢-混组合梁桥中纵桥向有钢主梁的约束，相对而言桥面板在横桥向上受的约束较弱，这一定程度加剧了剪力钉的横桥向徐变内力。

2.1.2 钢横梁剪力钉沿横桥向的内力变化规律

选取具有代表性的第1跨跨中截面、第1～2跨交界支点湿接缝截面，第2～3跨交界处湿接缝截面(固定支座处)的徐变内力进行对比(图6)。从图6中可知，3个控制截面的钢横梁上剪力钉的横桥向及顺桥向徐变内力在横截面上均呈现“中间小、两端大”的分布规律；受截面弯矩影响，跨中截面与支点截面上剪力钉的徐变内力的方向正好相反。此外，钢横梁上剪力钉沿顺桥向的徐变内力较横桥向大，表明在钢纵梁和钢横梁上的剪力钉中，剪力钉在钢梁轴线垂直的方向上的徐变内力更大，这可能是弯桥特有的现象，由“弯扭耦合”效应所导致。

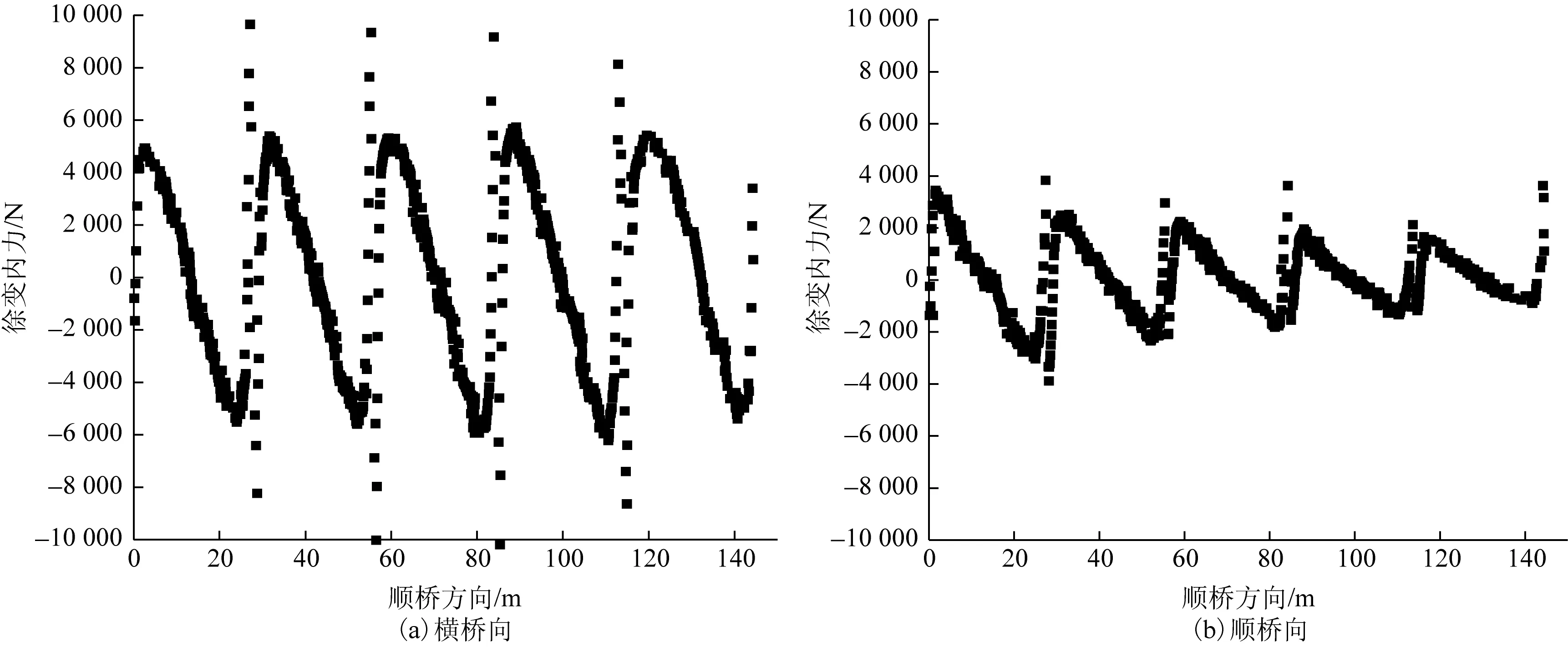
图4 外侧钢纵梁剪力钉徐变内力分布Fig.4 Internal force distribution of shear nail creep of external steel beam

图5 内侧钢纵梁剪力钉徐变内力分布Fig.5 Internal force distribution of shear nail creep of internal steel beam

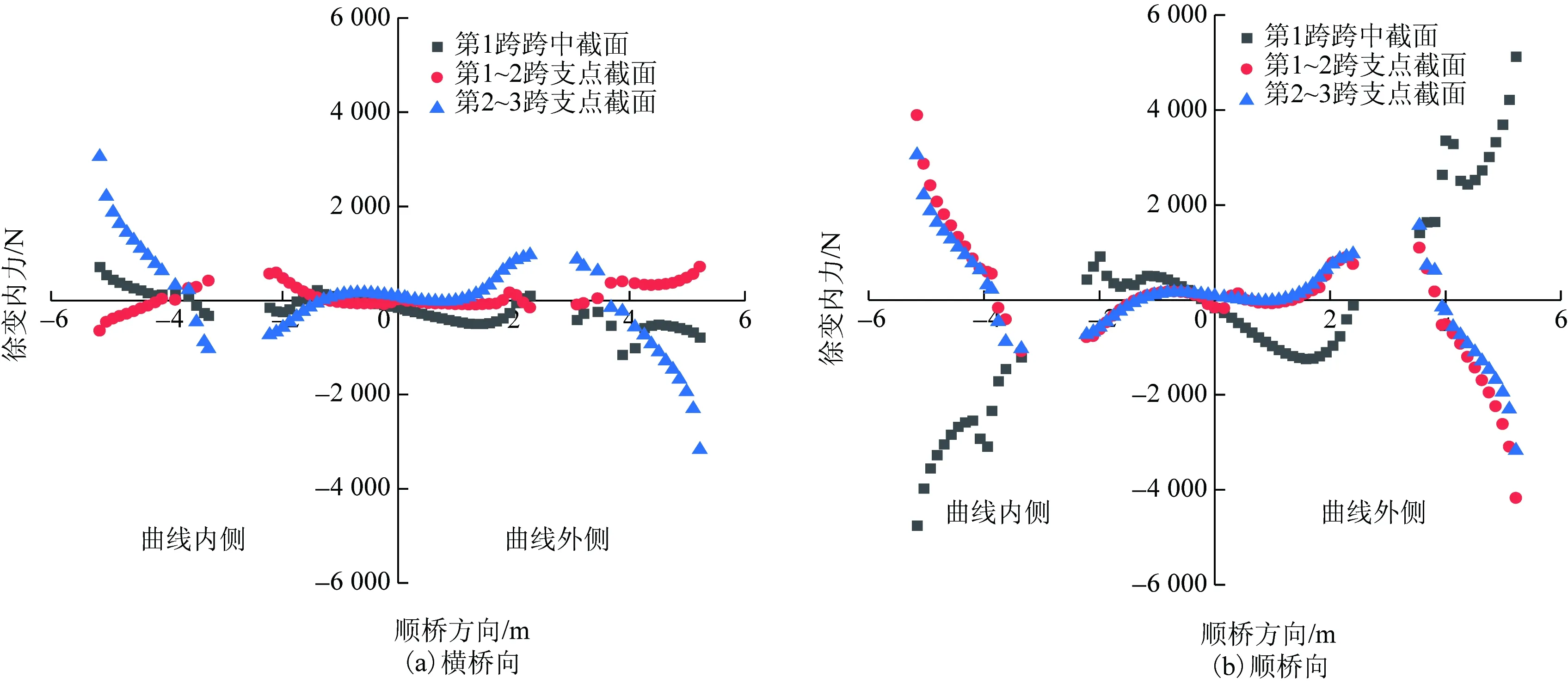
图6 横截面剪力钉徐变内力分布Fig.6 Internal force distribution of cross-section shear nail creep

2.2 剪力钉徐变滑移的空间分布

钢-混组合结构在混凝土板徐变影响下，剪力键发生变形导致混凝土板下缘与钢梁上缘之间产生相对滑移[18]，对结构受力产生不利影响。为探究徐变影响下剪力钉滑移情况，提取全桥剪力钉成桥初期和成桥10年时的剪力钉滑移量，按照式(7)做出剪力钉横桥向及顺桥向徐变滑移量云图(图7、图8)，直观得出徐变影响下剪力钉的滑移情况。

分析图7和图8可知：相比横桥向而言，剪力钉沿顺桥向的徐变滑移分布更加均匀、量值更小，同一剪力钉顺桥向的徐变滑移量仅为横桥向徐变滑移量30%～50%。在钢纵梁剪力钉沿横桥向的徐变滑移量中，边跨比中跨更大，滑移量极值出现在支点湿接缝附近钢梁处剪力钉上，且湿接缝两侧滑移方向相反，这与徐变影响下剪力钉受力是一致。钢横梁上剪力钉以桥面板横截面中线为界，在“弯扭耦合”效应影响下，钢横梁横截面中线内、外侧剪力钉滑移方向明显相反，且剪力钉顺桥向徐变滑移量极值出现于支点横内、外侧剪力钉处。

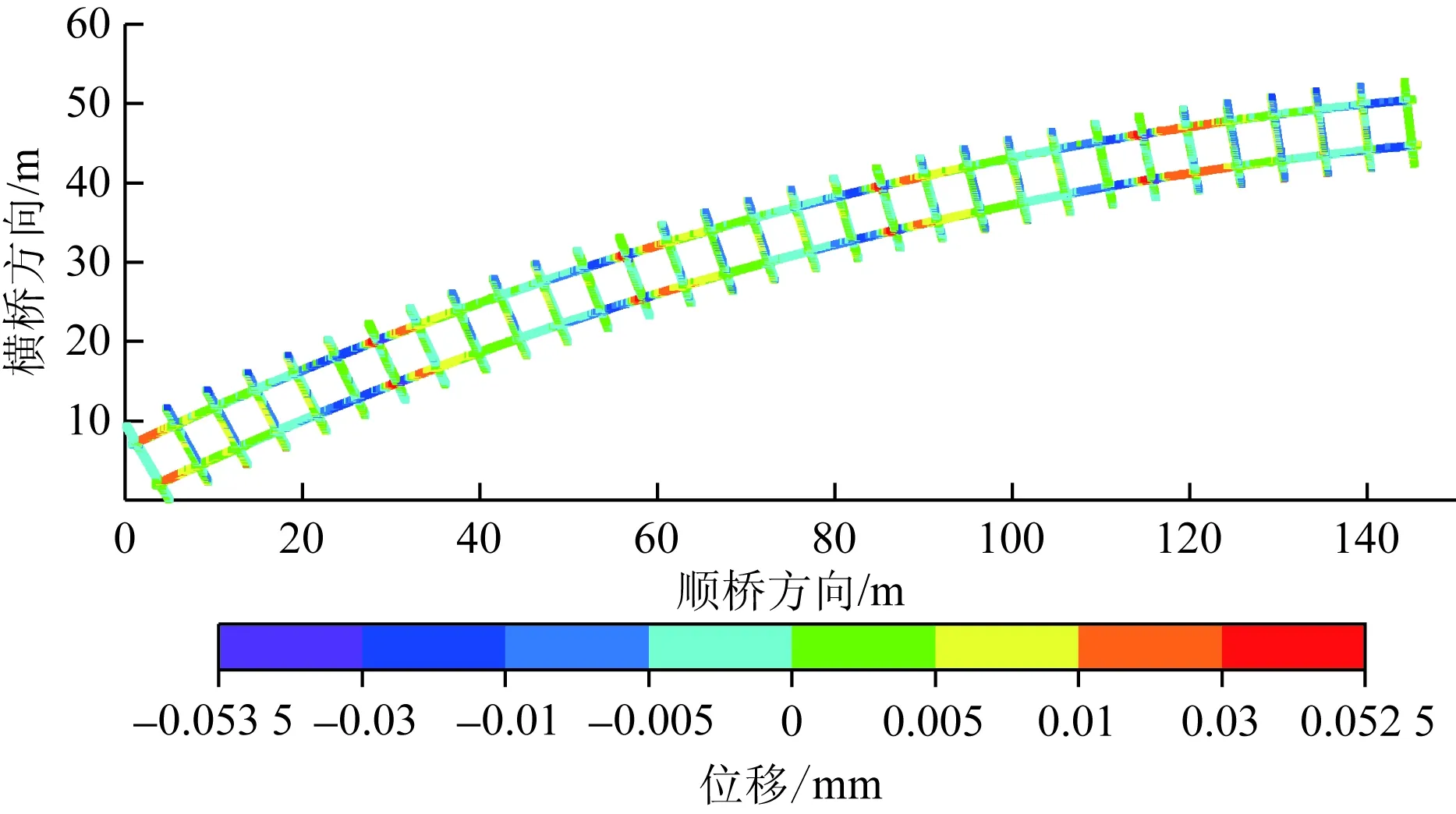
图7 徐变影响下剪力钉横桥向徐变滑移量云图Fig.7 Cloud image of shear nail cross-bridge creep under the influence of creep

图8 徐变影响下剪力钉顺桥向徐变滑移量云图Fig.8 Cloud image of shear nail creep along the bridge under the influence of creep

综上所述，剪力钉在横桥向和顺桥向的徐变滑移极值均出现在支点湿接缝附近，所不同的是，横桥向滑移极值出现在钢纵梁剪力钉上，而顺桥向滑移极值出现在钢横梁内、外侧剪力钉上，故支点湿接缝的钢纵梁及横梁区域应进行剪力钉的加密布置，以保证桥面板与下部结构的整体稳定性。

3 徐变影响参数分析

3.1 徐变影响时间历程分析

为探讨剪力钉徐变内力影响随时间的发展规律，选取龄期90 d桥面板分析湿接缝浇筑后的剪力钉徐变内力，对比由混凝土板徐变引起的不同位置、不同时长下剪力钉在横桥向的徐变内力(表2)。可以看出：混凝土板徐变对剪力钉内力的影响主要集中在成桥初期，特别是成桥第1年中；以外侧钢梁处剪力钉徐变内力为例，其第1年最大徐变内力值为8.618 kN，占到了成桥10年最大徐变内力值11.201 kN的76.9%。随着时间的推移，混凝土徐变发展趋于平缓，对剪力钉内力的影响较小；第10年剪力钉横桥向最大徐变内力值仅为0.081 kN，仅占成桥10年最大徐变内力值的0.7%，这充分说明同类型桥梁考虑10年的混凝土徐变影响是完全可以满足工程要求的。

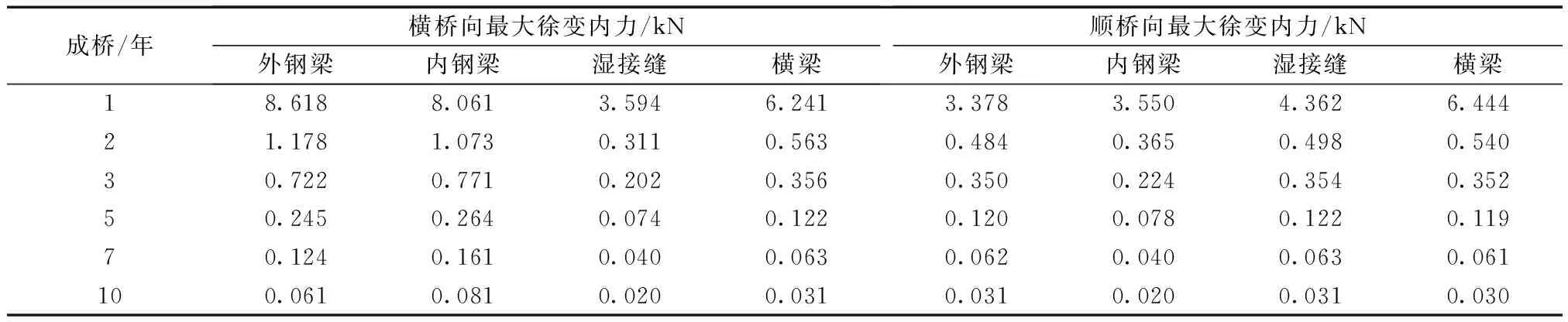
表2 不同年份徐变引起剪力钉最大徐变内力Table 2 Maximum creep internal force of shear nails caused by creep in different years

为进一步明确剪力钉徐变内力随时间的发展规律，选取受徐变影响较大的第2～3跨湿接缝截面(固定支座处)剪力钉，分析其成桥第1年中每30 d剪力钉横桥向徐变内力(图9)。可以看出，即使在徐变发展迅速的第1年，不同月份内剪力钉徐变内力依然存在较大差异，混凝土板徐变影响主要集中在成桥初期前3个月，此期间最大徐变内力为0.512 kN，占到了该截面剪力钉成桥1年最大徐变内力0.608 kN的84.2%。

图9 剪力钉横桥向徐变内力Fig.9 Internal force of shear nail creep in transverse directio

综上，预制桥面板存放90 d后再进行架设安装，其徐变对剪力钉内力影响仍然较大，且主要集中在成桥初期特别是前3个月，而后混凝土板徐变速率显著下降但持续时间较长。为防止局部剪力钉过载，造成桥面板与钢梁之间滑移过大，建议将桥面板预制龄期延长，并在存放期间维持较高湿度进行养护，以减少成桥期间混凝土板的徐变效应。

3.2 不同加载龄期下预制板徐变效应分析

随着时间推移，混凝土内部结构变得更加密实，强度不断提高，徐变效应也随之减弱[19]；为了降低混凝土板徐变效应对桥梁内力、挠度等的影响，预制桥面板达到规定强度后还需放置养护一段时间后再进行架设安装。为探究不同存放龄期下预制桥面板徐变效应对剪力钉内力的影响，本文中对比了桥面板存放龄期为30、90、180、270 d时全桥剪力钉的最大徐变内力Qmax和最大徐变滑移量Smax；为使结果更具有普适性，使用剪力钉最大抗剪承载力Qu对徐变内力进行无量纲化，相关结果见表3。

可以看出，随着桥面板龄期的增加，预制混凝土板徐变效应对剪力钉内力的影响也随之减弱。以剪力钉横桥向徐变内力为例，预制龄期为30 d时，最大徐变内力为13.470 kN，当预制龄期增加到90 d时，最大徐变内力为11.201 kN，减小的2.269 kN占预制龄期为30 d时最大徐变内力的16.8%。当预制混凝土板龄期增加到180、270 d时，与预制龄期为30 d时相比，其最大徐变内力减小值为3.845、4.499 kN，分别占到了预制龄期为30 d时最大徐变内力值的28.5%、33.4%。综上，增加预制桥面板的龄期可显著减小混凝土板徐变效应对剪力钉内力的影响，但随着龄期的增加徐变效应趋于平缓，考虑到存放预制混凝土板需要一定的时间及空间成本，综合经济性角度，推荐钢-混组合梁桥的预制桥面板养护180 d，可在减小徐变效应的同时兼顾成本。

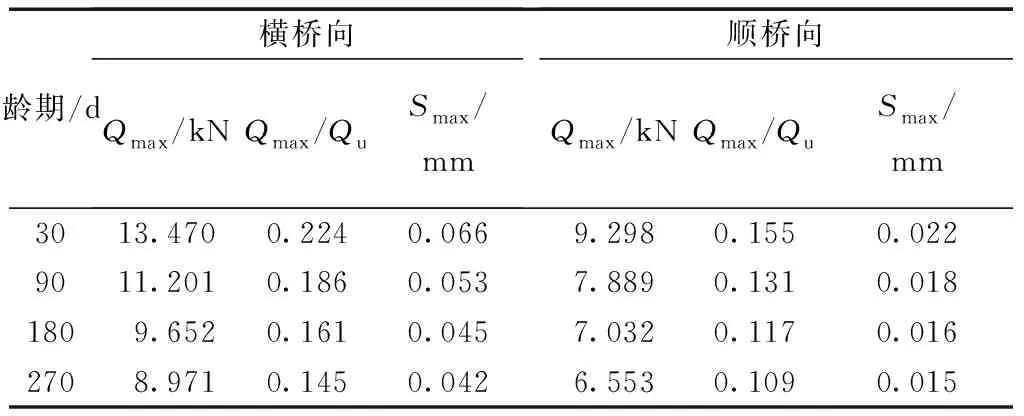
表3 不同预制龄期桥面板下剪力钉的受力行为Table 3 Stress behavior of shear nails in bridge deck of different prefabricated ages

4 结论

(1)考虑施工阶段的钢-混组合梁桥，钢纵梁处剪力钉横桥向徐变内力大约为顺桥向的2.0倍；与钢纵梁不同，位于钢横梁横截面两侧的剪力钉顺桥向徐变内力仅为横桥向的20%～40%。钢纵梁上剪力钉徐变内力由每跨跨中向两侧支点逐渐增大，且受现浇湿接缝的影响，徐变内力峰值多出现于支点湿接缝位置；钢横梁剪力钉徐变内力则由横截面中线向两侧逐渐增大，且受弯桥“弯扭耦合”效应影响，钢横梁横截面中线内、外侧剪力钉的徐变内力方向相反。

(2)混凝土板徐变效应导致的剪力钉滑移中，沿顺桥向的徐变滑移空间分布更为均匀，其滑移量仅为横桥向滑移量30%～50%。在剪力钉横桥向徐变滑移中，钢纵梁剪力钉滑移量明显大于钢横梁剪力钉，钢纵梁处剪力钉徐变滑移量由每跨跨中向支点两侧逐渐增大，滑移量极值出现于跨间支点湿接缝附近钢梁上。受“弯扭耦合”影响，钢横梁剪力钉内、外侧徐变滑移量数值相差不大但滑移方向相反，内侧区域剪力钉“向内”滑移而外侧区域剪力钉“向外”滑移。跨间支点湿接缝钢横梁剪力钉徐变滑移量显著大于跨中钢横梁剪力钉，全桥顺桥向徐变滑移量极值出现于跨间支点湿接缝横梁上。

(3)混凝土板徐变效应对剪力钉内力的影响主要在成桥初期，特别是成桥3个月内的徐变内力可占到成桥10年剪力钉徐变内力的84.2%，成桥3个月后混凝土板徐变效应对剪力钉内力影响较小但持续时间较长，成桥10年后混凝土板徐变效应对剪力钉内力影响微弱，可不再计入。增加预制桥面板加载龄期可显著降低徐变效应对剪力钉内力的影响，但这种下降趋势随龄期的增加而逐渐减弱，经对比兼经济性角度，推荐预制板存梁180 d并考虑10年的徐变效应，可满足工程实际要求。