一种融合遗传算法和二分法的船舶航速优化方法

赵 科， 张焱飞， 文逸彦

(1. 中国远洋海运集团有限公司， 上海 200127;2. 上海船舶运输科学研究所 航远技术与安全国家重点实验室， 上海 200135)

0 引 言

自2008年金融危机爆发以来，航运市场一直处于低迷状态，面对各种不确定因素和激烈的市场竞争，各航运公司不得不通过降低营运成本保持公司的利润[1]。对于散货船而言，燃油成本约占营运成本的50%，很多航运公司尝试通过技术改造、降速航行等方式降低油耗[2]。另外，全球气候的逐渐恶化促使国际海事组织(International Maritime Organization，IMO)制定了一系列关于碳排放的政策，引导全球航运业为控制气候变暖做出更多贡献[3]。例如：IMO海洋环境保护委员会(Marine Environment Protection Committee，MEPC)第75届会议引入了船舶能效指数(Energy Efficiency Existing Ship Index, EEXI)和碳排放强度指数(Carbon Intensity Indicator, CII)；RightShip制定了能效排放评估体系，评分越低，船舶可采用的航线和可航行的区域越少，相应的航运公司的市场越小[4]。因此，越来越多能耗控制法规的制定迫使航运公司采取更多的技术手段降低能耗。现阶段，对于营运船舶而言，降低船舶能耗的措施主要有更新主要设备、安装节能附体和采用航速优化方案等3种[5]。若采用更新主要设备和安装节能附体2种措施，需要航运公司专门安排船舶进坞修理，这会影响船舶的航次计划，且成本较高。相对而言，采用航速优化方案更为合适，能有效降低船舶营运能耗。

航速优化的难点是要充分考虑风、浪、流等海洋气象因素，在保证船舶、人员和货物满足安全性要求的前提下，优化船舶在整个航线上的航速，使燃油消耗最低。对于远洋船舶而言，由于航期较长，通常要求其在整个航次内不断地接收新的气象数据，用以更新航速优化建议。因此，构建精准的油耗预估模型、动态地更新海洋气象预报和采取合理的航速优化算法是远洋船舶航速优化的难点所在。国内外很多学者在开展航速优化研究时都以普通集装箱船或同一班轮的历史数据为基础构建油耗预估模型的经验公式，而超大型油船(Very Large Crude Carrier，VLCC)、超大型矿砂船(Very Large Ore Carrier，VLOC)和万箱级集装箱船等超大型船舶的数据更新速度较快且同类型船舶的数量较少，因此适用于普通船型的经验公式并不能应用于超大型船舶的计算中[5]。同时，很多学者在进行航速优化研究过程中采用历史气象数据验证航速优化算法的有效性，而实际中远洋船舶经历的气象情况是时刻变化的，计划航线上的气象预报数据也是时刻变化的，只有根据时刻变化的气象数据和船舶位置进行航速优化，才能充分保证船舶接收的航速优化建议是可靠的、准确的[5]。另外，航速优化是一个寻找全航线最优航速的过程，因此选用的航速优化算法需避免因陷入局部最优而无法进行迭代计算，同时还需考虑多个限制条件的影响，避免这些限制条件影响优化结果的准确性。

对此，本文以国际标准化组织(International Organization for Standardization, ISO)的ISO 15016—2015规范推荐的船舶风浪阻力计算公式为基础构建油耗模型。以遗传算法为基础，采用二分法对寻优个体的规模进行缩减，构建以油耗最低为目标的航速优化算法；以每日更新的气象信息和实船位置为基础，提供航速优化建议；通过数据对比，验证提出的航速优化方法的有效性。

1 油耗预估模型

构建油耗预估模型是确保航速优化效果良好的关键环节，油耗预报的精度决定着航速优化的可靠性，在相同的风浪条件下，油耗预估模型预估值偏高或偏低都会影响航速优化效果。简化油耗模型的难点有2个，分别是确定主机的输出功率和确定主机的燃油消耗率。燃油消耗率通常采用目标船给定的主机油耗率(Specific Fuel Oil Consumption, SFOC)曲线公式求取，不同的功率对应不同的消耗率，因此计算主机的输出功率是构建油耗模型的关键，既要考虑目标船的水动力性能，又要考虑船舶航行过程中遭遇的风浪对其主机输出功率的影响。本文采用直接功率法确定主机的输出功率，根据该方法，船舶在风浪中航行时，其主机输出功率主要由静水中的主机额定输出功率和风阻浪阻带来的功率增加值组成，即

P=Ps+Padd

(1)

式(1)中：P为主机总输出功率；Ps为静水中的主机额定输出功率，根据目标船型的自航模型水动力试验结果插值得到；Padd为风阻浪阻带来的功率增加值。Padd的计算公式为

Padd=(Rwind+Rwave)vs/ηD

(2)

式(2)中：Rwind为风阻；Rwave为浪阻；vs为对地航速；ηD为推进效率。Rwind和Rwave采用ISO 15016—2015推荐的风阻浪阻增加公式[6]计算，即

(3)

(4)

最终，将主机总输出功率代入目标船主机的SFOC公式中，获得油耗值F。

F=SFOC(P)

(5)

式(3)～式(5)中：vg为对水航速；ρA为空气的密度；CAA为风阻系数；vWR为参考高度的相对风速；ψWR为参考高度的相对风向；AXV为迎风横截面面积；ρs为水的密度；g为重力加速度；H1/3为有义波高；B为型宽；LBWL为船首至95%型宽处的水线长度；F为燃油消耗。

2 融合遗传算法与二分法的航速优化算法

2.1 遗传优化算法

遗传优化算法是美国学者Holland在20世纪70年代提出的，其寻找最优解的基本原理借鉴了达尔文进化论中物竞天择的自然优化法则[7]。首先确定适应度；然后通过复制、杂交和变异等操作将父代中较为优秀的个体遗传给下一代，淘汰不良基因，从而提高整个群体的适应度；最后一代又一代地进化，直至达到规定的适应度或完成规定的迭代次数。优化结束时，将最后得到的种群中适应值最大的个体作为优化问题的最优解。

遗传算法所具有的以下特点可避免出现局部最优解：

1) 遗传算法可进行多峰搜索，避免出现单峰搜索时出现的极值点；

2) 遗传算法是基于概率规则得到的，能避免出现确定性规则下易出现的局部缺陷；

3) 对于复杂目标函数，遗传算法根据适应度计算结果进行选择。

在实际工程应用中，利用遗传算法解决最优问题的步骤如下：

1) 确定初始种群；

2) 定义适应度函数，利用适应度函数有效筛选群体中的个体，以获得具有较高适应度的个体，并将其遗传给下一代；

3) 下一代继承上一代的基因，并继续杂交、变异和重组，进化出适应度更高的个体；

4) 根据筛选条件，保留适应度更高的个体，进化产生下一代种群；

5) 重复上述步骤，直至满足需求或获得适应度最高的种群。

遗传算法流程图见图1。

图1 遗传算法流程图

2.2 二分法

二分法即折半法，是一种在特定顺序中进行有序搜索的方法。特别是对于数据量较大，需对处理的时间复杂度进行优化的情况而言，二分法是一种较为高效的搜索方法，每次搜索可抛弃1/2的搜索区间，缩小搜索的范围[8]，提高搜索效率。

在待定数据范围内利用二分法搜索，逐步缩小搜索范围，直至确定有无记录位置，主要流程如下：

1) 取特定顺序数组中间位置的元素与目标元素相比较，若中间元素恰好是给定的目标元素，则结束搜索，否则继续进行下一步操作。

2) 若目标元素大于中间元素，则在数据大于中间元素的半区搜索；若目标元素小于中间元素，则在数据小于中间元素的半区搜索，以此重复上一步操作。

3) 若中间一步为空，则表示找不到目标元素。

2.3 航速优化算法

根据营运船舶的航次计划，利用实时更新的气象预报数据为目标船提供全航路航速优化建议。以航次计划中的到达时间和转速禁区为基本限制条件，以目标船的装载信息和航路气象信息为优化变量，以全航路油耗最低为目标函数，进行航速全局优化。

首先，将整个航线等分为N个分段，从而获得N个分段总油耗的最小值。每个航段在遗传算法中代表1个个体，对于航程超过5 000 n mile的远洋航线而言，细分出更多的分段有助于更充分地计算各分段遭遇的气象条件对油耗的影响，从而获得更精确的优化结果。然而，划分的分段越多，计算效率越低。因此，为进一步提升遗传算法的优化精度和计算效率，采用二分法对寻优个体的规模进行缩减，即将整个航线划分为2个分段，先对后半航段采用1个转速进行规划，再将前半航段等分为2个分段，对划分后的前半航段中的后半航段采用1个转速进行规划，直至划分到最小的航段。以1 000 n mile的航线为例，100 n mile为最小划分距离，按常规方法需划分10个分段进行优化，而采用二分法划分的航段为5个，见图2。

图2 二分法缩减个体数量示意

其次，根据遗传算法的规则，初步设定各分段的转速范围和初始化转速值。以该航线的起点要求时间和结束点时间为约束条件，以完成该航次消耗的总燃油最低为目标，对该航线各等分段的航速进行优化，得出最低油耗下各分段的主机转速。建立对应优化问题的数学模型，有

(5)

Level(wind)i≤Setlevel(wind)

(6)

Level(wave)i≤Setlevel(wave)

(7)

(8)

Nmsi∉NB

(9)

式(5)～式(9)中：min Oil为优化的目标函数；Level(wind)i为第i个优化转向点处遭遇的风级；Level(wave)i为第i个优化转向点处遭遇的浪级；Setlevel(wind)为本航次设定的最大许可风级，对于本船压载状态，设置为7级；Setlevel(wave)为本航次设定的最大许可浪级，对于本船压载状态，设置为5级；Distancei为第i个优化转向点与第i-1个优化转向点之间的距离；vi为第i个优化转向点与第i-1个优化转向点之间的优化预估航速；Navtime为航行计划时长，等于预计到达时间减去预计出发时间；Nmsi为第i个优化转向点与第i-1个优化转向点之间的优化预估转速；NB为目标船主机的转速禁区。

3 航速优化效果实船验证

在目标船开航之前，根据制订的航次计划和船舶装载数据确定整个航路的基本限制条件。在目标船开航之后，根据实船采集的航行数据和实时更新的气象数据，每日动态调整剩余航线的航速优化建议，并定时将其推送至船端。具体的实船航速优化流程见图3。

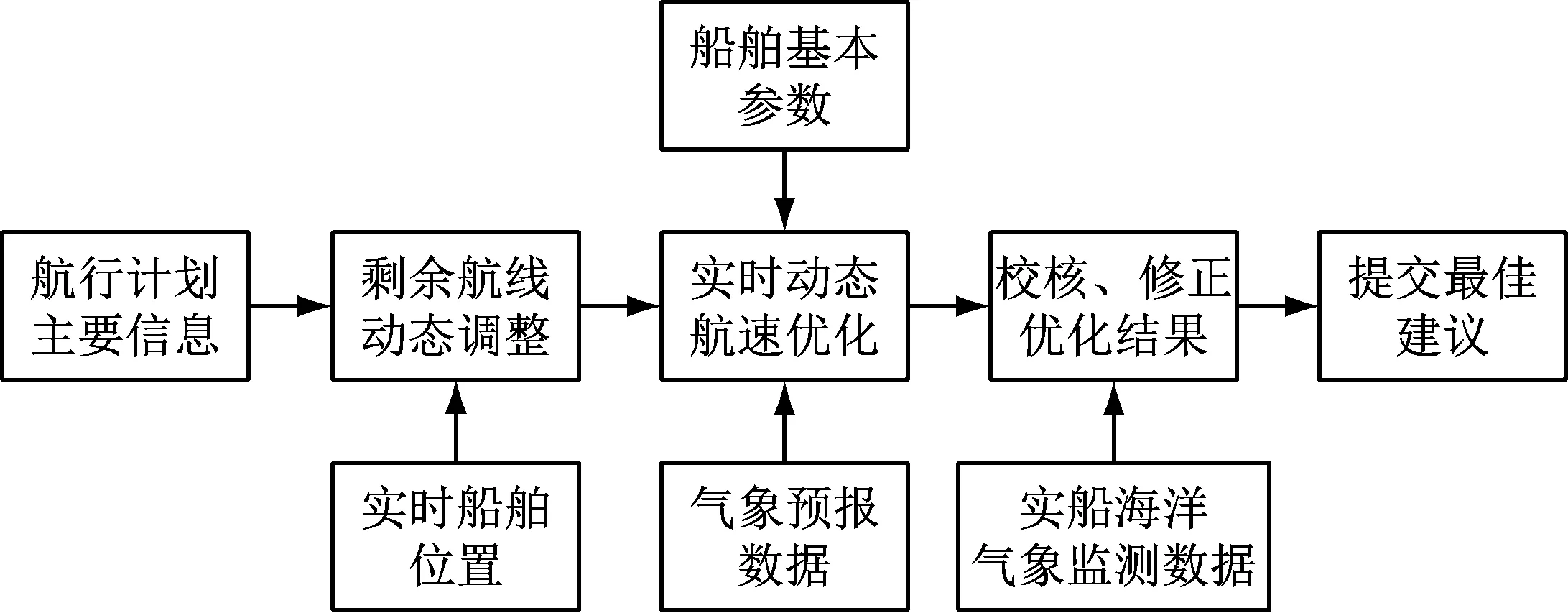
图3 实船航速优化流程

每日推送给船端的航速优化建议包含剩余航线各转向点遭遇的风浪数据、预估油耗、剩余里程、推荐转速和预估航速等信息。

整个航次结束之后，选择载况相同的历史航次进行对比，验证本文提出的航速优化方法的节能效果。该目标船装有航行数据实时采集系统，能将航行数据实时发送给岸端数据管理平台。为更好地验证优化效果，选取稳定的航行阶段作为比较对象，从而筛选出停泊或航行异常产生的异常油耗。此外，为进一步验证航速优化的效果，采用ISO 15016—2015给定的风阻浪阻计算方法对船舶遭遇的气象条件进行修正，将对比航次遭遇的气象条件修正为与优化航次相同的气象条件，对比结果见表1。由表1可知：优化航次的航行距离(总里程)为11 615 n mile，平均航速为10.54 kn，总油耗为2 087.49 t；对比航次的总里程为12 010 n mile，平均航速为10.14 kn，总油耗为2 446.27 t；修正之后优化航次的节能效果达到8.9%。因此，以航次油耗最低为目标，融合遗传算法和二分法的航速优化方法具有很好的节能效果。

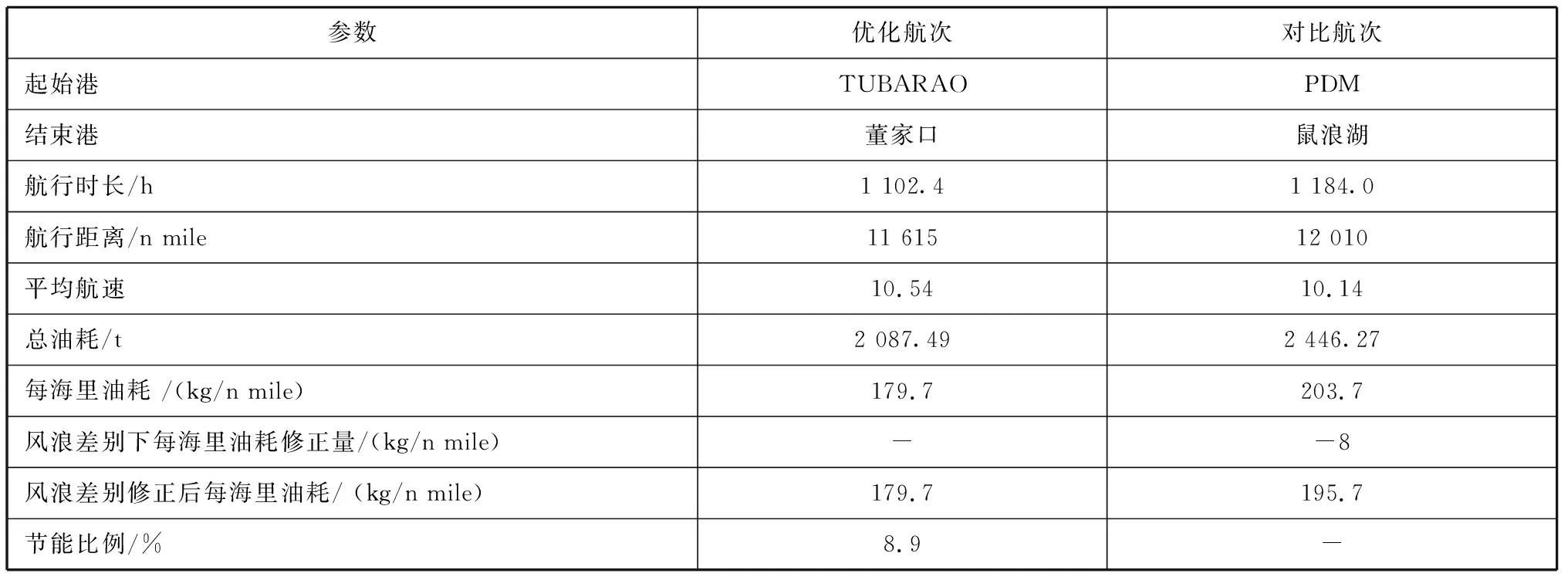
表1 对比航次统计数据及节能效果

4 结 语

本文以营运船舶油耗最少为目标，提出了融合遗传算法和二分法的航速优化方法，比较了实船优化航次与对比航次采集的航行数据，结果表明，该航速优化方法的节能效果良好，具有较高的应用价值。同时需看到，目前航速优化方法中的油耗、风阻和浪阻的计算均是基于船模水池水动力试验数据和国际通用的经验公式进行的，而这些计算公式能否适用于各种船型有待进一步考证，且在风浪条件下对船舶失速的影响需深入研究。未来，通过融合实船数据、船模水动力试验数据和主机台架数据进行更深层次的研究，有望提供更符合目标船实际航行情况的航速和转速优化建议，进一步提升航速优化的节能效果。