基于时空注意力图卷积神经网络的交通速度预测
2022-01-01黄伟坚李春贵
黄伟坚 李春贵


摘 要:交通速度是衡量交通状态的一个重要指标,实时、准确的交通速度预测是构建智能交通系统的重要一环。针对交通速度存在随机性、非线性、时空相关性等问题,提出了一种新的基于注意力机制和图卷积神经网络相结合的交通速度预测模型。首先,使用注意力机制构建时空注意力权重矩阵,再联合图卷积方法捕获交通信息中的空间相关性特征;然后,通过门控时卷积的方法获取时间相关性;最后,将所提模型与其他5个基准模型分别在2组公开的交通速度数据集上进行预测。实验结果表明,该预测模型在2个数据集上的准确率分别为75.1%和86.6%,比先进的基准模型的准确率高3%左右。说明所提模型具有较高的准确率和稳定性,可为交通管理提供科学依据。
关键词:交通速度预测;注意力机制;图卷积;时空相关性
中图分类号:TP183;U491.2 DOI:10.16375/j.cnki.cn45-1395/t.2022.01.009
0 引言
交通在日常生活当中起着至关重要的作用,构建健康有序的智能交通管理系统,缓解交通拥堵成为了当今社会的迫切需求。交通速度是反映交通状况的一个重要因素,精准的交通速度预测不仅可以为交通管理者提供科学的交通规划依据,还可以为出行者规划出行路线,从而有效地缓解交通拥堵问题。交通速度作为交通流的主要参数,反映交通路网的服务水平。然而,由于交通路网在不同时段的交通道路之间存在着不同的交通状态,在路网中不同位置的车辆速度也存在显著的差异性,因此,交通速度具有复杂的时空相关性。
目前常见的交通预测模型分为3大类:基于統计理论方法的模型、基于传统机器学习方法的模型、基于深度学习方法的模型。随着互联网的发展和大数据时代的到来,交通数据量急剧增长,一些传统的交通预测方法难以在智能交通的实际应用中达到满意的效果,因此,基于深度学习的算法模型成为了研究热点。近年来,基于神经网络方法的循环神经网络(RNN)在自然语言处理领域中应用甚广。Ma等[1]首次提出了将长短期记忆网络(LSTM)应用于交通速度预测,利用循环神经网络捕获交通速度在不同时间片段中的潜在相关性,并取得不错的预测效果。Fu等[2]利用LSTM和门控循环神经网络(GRU)进行短时交通流预测,实验结果表明,基于LSTM和GRU等循环神经网络的预测效果优于传统的时间序列模型。秦胜君等[3]提出基于LSTM模型的交通轨迹异常挖掘模型,提高了异常检测的精度。虽然循环神经网络常被用于处理时序数据,但其本身存在着梯度消失和梯度爆炸的风险。为了同时捕获交通数据中的空间相关性和时间相关性,罗文慧等[4]通过结合卷积神经网络(CNN)和支持向量回归(SVR)的方法用于交通流预测,利用一维CNN来捕获交通路网下的空间相关性,通过SVR模型挖掘交通流量的时间变化特征。由于交通数据不是标准的网格数据,交通网络具有复杂的拓扑结构,因此,基于CNN的预测方法具有局限性。Yu等[5]提出STGCN模型,通过使用图神经网络和普通一维卷积神经网络进行交通速度预测。虽然该方法使用了图神经网络来捕获交通信息的空间特征,但是,该模型在时间维度上还是延续传统的一维卷积神经网络,导致模型在获取交通信息的时间相关性方面受限。为了避免传统CNN和RNN存在的缺点,更好地捕获交通数据中的时空相关性,本文将提出一种新的基于注意力机制和图卷积神经网络相结合的交通速度预测模型,用于提高交通速度预测的准确率。
1 问题描述与模型构建
1.1 问题描述及定义
以交通速度预测作为目标。交通速度预测是指根据道路上交通速度的历史数据来预测未来一段时间的交通速度,如式(1)所示:
[[Xt+1, Xt+2, …, Xt+P]=f(Xt?t?, …, Xt?1, Xt)], (1)
其中:[t?]表示输入的时间序列长度,[P]表示被预测的时间序列长度,[X∈? N×t]为特征矩阵,[?]为实数集,[N]为道路总数,[t]为历史数据的时间序列总长度。
交通路网具有拓扑特性,使用图[G=(V, E, A)]来表示路网结构,如图1所示,将每一段交通道路假设为一个节点,[V]表示所有节点的集合,[V=(v1, v2, …, vN)],[N]为道路总数,道路之间通过边来连接,[E]表示边的集合。用邻接矩阵[A∈?N×N]表示道路之间的连通关系,[Wij]表示节点[i]到节点[j]的权重关系。
1.2 模型结构
由于交通速度预测问题存在着复杂的时间相关性和空间相关性,为了提高预测准确率,降低训练误差,提出一种新型的交通速度预测模型:基于时空注意力机制下的图时序卷积神经网络模型(ST-AGTCN)。ST-AGTCN包含3大模块:1)注意力模块,利用注意力机制模块,通过对输入的交通数据进行学习,从而构建出时空注意力矩阵[S'];2)GCN模块,使用与切比雪夫多项式近似的GCN方法来获取交通数据的空间相关性特征;3)门控时卷积模块,通过门控时卷积捕获交通数据的时间相关性特征。ST-AGTCN模型总体框架如图2所示。
1.3 注意力模块
由于交通路网信息随时间动态变化,因此,在不同的时间段中,每个节点的相关性权重是动态变化的。注意力机制的核心思想是根据输入数据自适应地关注最相关的特征。本文使用Soft-attention机制[6],构建时空注意力权重矩阵,动态地捕获交通速度在交通网络上的时空相关性特征。
在时间维度上,不同时间段之间的交通速度存在着相关性。通过注意力机制对输入数据赋予不同的时间相关性权重[7],可根据当前的输入数据动态调整时间注意力矩阵[W],如式(2)所示:
[W=Vt?σ((XTU1)U2(U3X)+bt)], (2)
式中:[W∈?t?×t?]是时间相关性的权重矩阵;[X∈?N×t?]是输入的特征矩阵;[Vt, bt∈?t?×t?]、[U1∈?N]、[U2∈?C×N]、[U3∈?C],为该注意力网络的可学习参数;[N]为节点数;[t?]表示输入的时间序列长度;[C]为特征通道数,在本文中,设[C]=1。
使用softmax函数对时间注意力矩阵进行归一化处理,然后对输入数据进行时间相关性加权处理来动态调整输入数据,如式(3)所示:
[W'i, j=exp(Wi, j)j=1t exp(Wi, j)], (3)
[Xh=(X1, X2, …, Xt?)=(X1, X2, …, Xt?)W'] , (4)
式中:[Wi, j∈?t?×t?]表示第[i]个时间段和第[j]个时间段的交通速度的时间相关性矩阵,[Xh∈?N×C×t?]表示在时间维度上动态调整后的特征矩阵。
在空间维度上,由于不同路段之间的交通状态互相影响,因此,使用注意力机制对不同节点构建权重矩阵,如下所示:
[S=Vs·σ((XhQ1)Q2(Q3Xh)T+bs)], (5)
[S'i, j=exp(Si, j)j=1N exp(Si, j)] , (6)
其中:[S∈?N×N]是时空注意力矩阵,根据当前的 输入动态来计算;[Vs,bs∈?N×N]、[Q1∈?t?]、[Q2∈?C×t?]、[Q3∈?C]为注意力网络的可学习参数;[Xh∈?N×t?]是在时间维度上处理过的输入数据,将[Xh]作为当前层的输入,计算出时空注意力矩阵[S],然后使用softmax函数对时空注意力矩阵进行归一化处理;[S'i, j]矩阵元素的数值大小表示对应节点[i]和节点[j]之间时空相关性强度。基于Guo等[8]的研究,当执行图卷积操作时,联合注意力矩阵[S'i, j]动态提取交通数据的空间特征。
1.4 图卷积模块
如何利用交通网络各观测节点之间的空间相关性一直是交通预测中重点研究的问题。卷积神经网络(CNN)在计算机视觉领域中得到了很好的应用[9],但是CNN模型只适用于在欧式空间中处理网格数据,并不适用于具有复杂拓扑结构的交通网络。如图3所示,图像数据属于网格数据,而交通数据是具有拓扑结构的图数据。近年来利用图卷积神经网络(GCN)的方法处理具有拓扑结构的图数据受到了广泛关注。GCN 分为2个主流派:基于频谱图理论的方法[10]和基于空间域的方法[11]。本文将采用基于频谱图理论的方法从交通数据中提取空间特征。
在谱图分析中,图由其对应的拉普拉斯矩阵表示。图拉普拉斯矩阵定义为:
[L=D?A] , (7)
标准化的拉普拉斯矩阵定义为:
[L=IN?D?12AD?12=UΛUT] , (8)
式中:[IN]为单位矩阵,[A∈?N×N]为邻接矩阵,[D∈?N×N]为度矩阵,[Λ]为[L]矩阵的特征值组成的对角矩阵。
在频谱图理论中,输入特征[x∈?N×t?]被视为图上的信号,信号[x]通过图形傅里叶变换被变换到谱域。GCN是通过在傅里叶域中对角化的线性算子来代替经典卷积算子而实现的卷积运算[12]。信号[x]在图上的卷积操作表示为:
[gθ?Gx=gθ(L)x=gθ(UΛUT)x=Ugθ(Λ)UTx]. (9)
如式(9)所示,[gθ]为卷积核;[?G]表示图形的卷积运算;[L∈?N×N],为图拉普拉斯矩阵;[Λ∈?N×N];[UTx] 表示[x]的傅里叶变换。
当图的规模较大时,计算[L]矩阵特征值分解的复杂度会变得很高。为了解决特征值分解计算成本高的问题,采用切比雪夫多项式近似的GCN方法有效地解决了这个问题[13]。如式(10)所示:
[gθ?Gx=gθ(L)x≈k=0k?1 θktk(L)x] , (10)
式中:[θk∈?k]是切比雪夫多项式的系数向量,[L=2L/λmax?In],[λmax]是拉普拉斯矩阵[L]的最大特征值。切比雪夫多项式的递归定义为:
[tkx=2xtk?1x?tk?2x], (11)
其中:[t0x=1],[t1x=x]。本文通过切比雪夫多项式近似方法完成图卷积运算,将中心节点周围0到k -1阶的邻居节点的相关信息进行聚合。
为了动态调整邻居节点之间的相关性,将时空注意力矩阵[S'∈?N×N]与切比雪夫多项式[tk(L)]相結合。最终,GCN公式如式(12)所示:
[gθ?Gx=gθ(L)x=k=0k?1 θk(tk(L)⊙S')x] , (12)
其中,[⊙]为哈达玛积(Hadamard product)。在捕获了节点之间的空间相关性之后,将GCN的输出进一步堆叠到门控时卷积模块;通过门控时卷积模块,进一步提取交通数据在各个时间片段上的时间相关性特征。
1.5 门控时卷积模块
交通数据是一组时间序列数据,有着复杂的时间相关性。传统的CNN处理时间序列数据具有效率低、信息易泄露等风险。由于CNN只能通过不断增加卷积层和增大卷积核的方式才能扩大感受野,所以很难提取长时间序列的时间相关性特征。常用于处理长时间序列的循环神经网络方法有着梯度爆炸和梯度消失等缺点[14]。为了解决上述问题,受wavenet模型的启发[15],采用门控时卷积的方法来捕获交通数据的时间相关性特征;使用扩张因果卷积作为时间卷积网络(TCN),用于捕获交通数据在时间片段上的变化趋势,如图4所示。
TCN通过控制扩张因子的大小和增加层的深度使感受野以指数级放大,从而减少网络叠加层数,减少了模型的参数量。扩张因果卷积操作如式(13)表示:
[x?f(t)=s=0l?1 f(s)x(t?d×s)], (13)
式中:[x∈?t] 为当前的输入数据;[f∈?l]为卷积操作的滤波器;[d]为扩张因子,用于控制空洞数量;[l]表示卷积所在的层数。
门控时卷积模型是基于TCN的变形。门控时卷积模型由两部分组成,如式(14)所示:
[hout=g(Θ1?X+a)⊙σ(Θ2?X+b)], (14)
式中:[?]表示卷积操作;[Θ1]、[Θ2]、[a]、[b]为模型参数;[g]是一个tanh激活函数,用来增加非线性;[σ]是一个sigmoid函数,是一个滤波器,用于过滤无用信息,保留有用信息。门控时卷积模型结构如 图5所示,[1*1]是一个全连接层,用来调整输入的 维度。
经过门控时卷积提取时间特征后,在输出处增加一个ReLU 激活函数。之后,再经过一个全连接层,通过线性变换得出最终的输出结果,如式(15)所示:
[Output=Linear(ReLU(hout))]. (15)
2 ST-AGTCN模型训练
2.1 实验数据的选取
为消除非典型车流量的影响,以工作日的交通速度作为研究目标,选取了国内和国外2个公开数据集来评估模型的预测性能。
SZ-taxi数据集:该数据集采集了深圳市罗湖区2015年1月1日—1月31日所有工作日的出租车轨迹数据,并选择罗湖区的156条主要道路作为研究区域,将采集到的数据样本每15 min聚合一次。该数据集包含2个数据矩阵,一个是特征矩阵X,该矩阵描述了每条道路在不同时段的交通速度,矩阵的每一行数据表示每段交通道路在该时段的交通速度,每一列数据表示同一段道路在不同时段的交通速度;另一个数据矩阵是156[×]156的邻接矩阵A,该矩阵用0和1描述道路与道路之间的连接 关系。
PeMSD7数据集:该交通速度数据集由美国加州交通运输部在加州第七区通过228条道路的交通传感器采集,并将采集到的数据样本每5 min聚合一次。PeMSD7数据集记录了加州第七区2012年5月1日—6月30日的车辆速度。该数据集包含2个数据矩阵,同上所述,一个是特征矩阵X,另一个是228[×]228的节点距离矩阵,邻接矩阵A是根据交通路网中站点之间的距离计算的,计算公式如 式(16)所示:
[Aij=exp (?dijσ2), i≠j and exp(?dijσ2)≥?0, otherwise], (16)
式中:[Aij]表示节点[i]和节点[j]的连通关系;[dij]表示节点之间的距离;[σ2]、[?]是控制邻接矩阵[A]的分布和稀疏性的阈值,按照经验将2个阈值分别设置为[σ2=10]、[?=0.5]。
为了减小预测误差,利用min-max标准化方法对原始数据进行标准化,使其落到[0,1]内,如 式(17)所示:
[z=x?xminxmax?xmin], (17)
式中:[z]表示归一化后的数据,[x]为原始数据,[xmin]为原始数据的最小值,[xmax]为最大值。本文将数据集进行划分,80%数据作为训练集,20%数据用作测试集,通过ST-AGTCN模型预测各路段未来 15 min、30 min的交通速度。
2.2 实验环境与参数设定
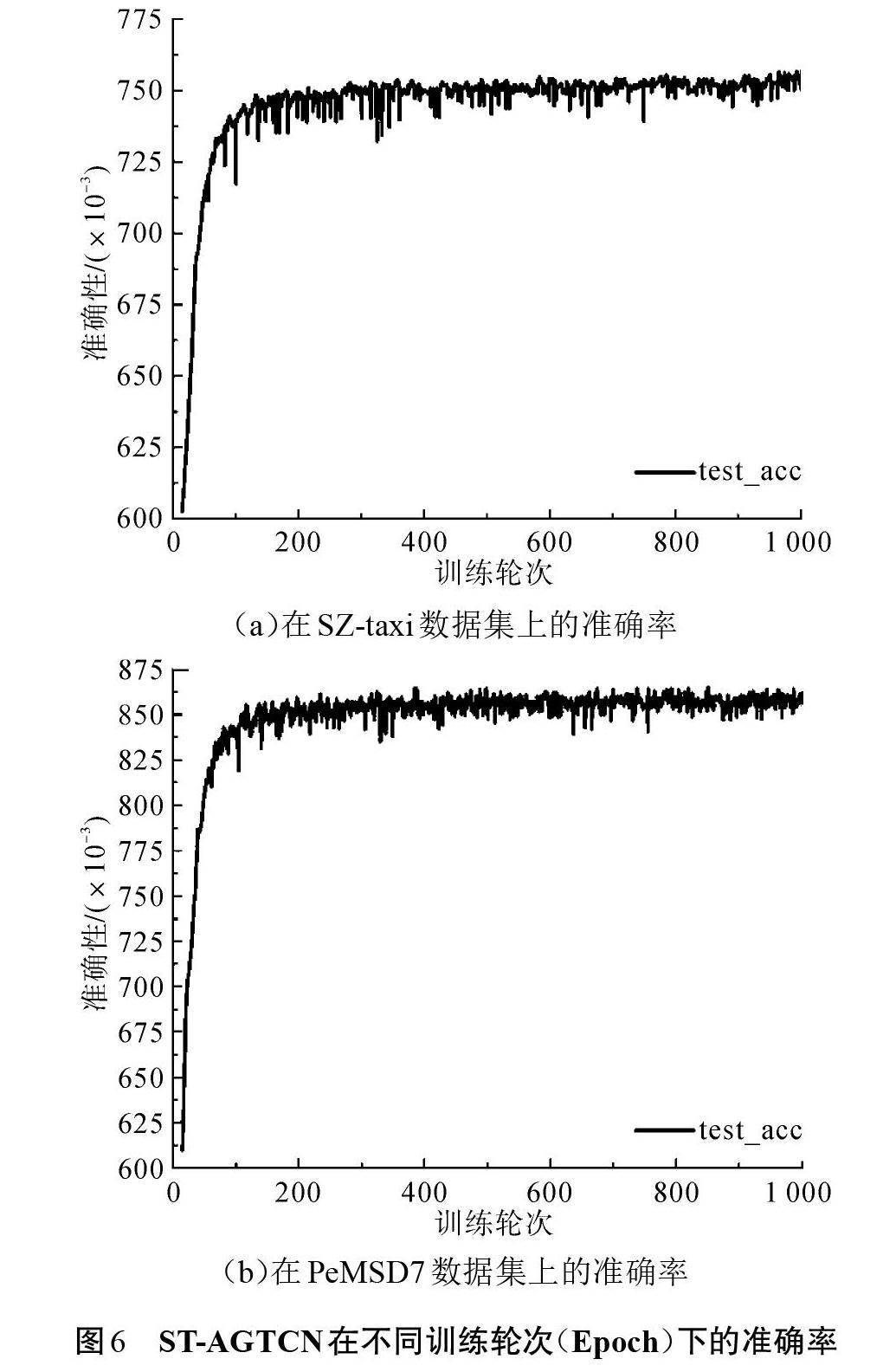
实验在Ubuntu20.04.2操作系统中的PyCharm2020.2.1社区版的环境下进行,Python 版本为3.7,Intel(R) Core(TM) i7-8700 CPU @ 3.20 GHz,运行内存16 GB,显卡型号为GTX TITAN X,显存为12 GB。使用Pytorch 深度学习框架来搭建ST-AGTCN模型,其中还使用到了数学工具包Numpy和Pandas,并将机器学习库Scikit-learn用作属性的预处理工作和相关机器学习模型的实现。在本实验中,使用12个历史观测数据作为单次输入大小,即[t?=12],输入批量大小设置为32。考虑到计算效率和预测性能的提高程度,在图卷积模块,对切比雪夫多项式在[k={1,2,3,4}]的情况下进行了实验。当[k=3]时,模型训练效果最佳。在门控时卷积模块中的时卷积网络中使用了8层,每层的扩张因子设置为[1,2,1,2,1,2,1,2],卷积核大小设置为3,卷积核个数为64。选择Adam优化算法作为优化器,初始学习率设置为[γ=0.001],正则化超参数设置为[λ=0.001 5],将训练轮次设置为1 000次。如图6所示,在训练过程中,当训练轮次为 1 000时,ST-AGTCN预测模型的准确率最高且趋向于稳定。
2.3 损失函数
在模型训练过程中,本实验的训练目的是降低交通速度真实值和预测值之间的误差。ST-AGTCN的损失函数如式(18)所示:
[loss=||Vt?Vt||+λLreg], (18)
式中:[Vt]是实际交通速度值;[Vt]是预测值;[Lreg]是[L]2正则化项,用于防止过拟合;[λ]是一个正则化超参数。
2.4 性能评估指标
为了评估不同模型的预测效果,采用3种常用于评价回归任务效果的评价指标。
[△]为平均绝对误差(MAE),计算公式如下:
[△=1ni=1n Vi?Vi]. (19)
[σ]为均方根误差(RMSE),[σ]对预测高速度值比较敏感,即当较差的预测模型在预测高速度值时会出现比较大的[σ]值,计算公式如下:
[σ=1ni=1n (Vi?Vi)212]. (20)
[A]为准确率(Accuracy),模型预测性能越好,准确率越高,计算公式如下:
[A=1?||V?V||F||V||F]. (21)
3 实验结果与分析
为了更直观地观测ST-AGTCN模型的预测效果,在SZ-taxi数据集和PeMSD7数据集上分别选取一条道路,并将ST-AGTCN模型在15 min时间序列上的预测结果进行可视化。如图7所示,图中的黑色实线是真实的交通速度值,绿色实线为 ST-AGTCN模型的交通速度预测结果。从图中可以看出,绿色线条的变化趋势和黑色线条的变化趋势基本吻合,说明了ST-AGTCN模型拥有不错的拟合效果,并在交通速度预测任务中表现良好。
将ST-AGTCN模型的预测性能与以下5个基准模型进行比较:
1)HA:历史平均法[16],该模型用同时刻的历史数据求平均的方法来预测未来时刻的交通数据。
2)ARIMA:自回归综合移动平均法[17],一种时间序列预测模型,将时间序列拟合到参数模型中,对未来时刻的交通数据进行预测。
3)SVR:支持向量回归模型[18],使用核函数将数据从低维空间映射到高维空间,通过线性支持向量机的方法获得输入与输出之间的关系,对未来时刻的交通数据进行预测。
4)STGCN:时空图卷积模型,该模型通过使用GCN和普通一维CNN进行交通速度預测。
5)T-GCN:时间图卷积模型[19],该模型通过使用GCN和GRU相结合的方法进行交通速度预测。
在表1和表2中记录了ST-AGTCN模型和其他5个基准模型分别在2个交通速度数据集上进行15 min和30 min交通速度预测的结果。
1) 训练误差:训练误差越小,模型的预测性能越好。从表1和表2的数据可看出,ST-AGTCN 模型的MAE误差和RMSE误差的值在15 min和30 min的交通速度预测任务中均比其他模型小。如图8所示,图8(a)和图8(b)显示了各个模型在SZ-taxi数据集上的RMSE值,图8(c)和图8(d)显示了各个模型在PeMSD7数据集上的RMSE值。从图8可以看出,ST-AGTCN的RMSE值在所有模型当中最小,说明ST-AGTCN模型的预测性能优于其他5个基准模型。
2)传统模型的评估:从表1和表2 的数据可以看出,在15 min和30 min的交通速度预测任务中,从预测性能上来看,基于深度学习方法的模型在交通速度预测任务中比传统的机器学习模型和时间序列模型性能更好。STGCN、T-GCN、ST-AGTCN都是基于深度学习方法的模型,SVR是传统机器学习模型,HA和ARIMA是传统的时间序列分析模型。在SZ-taxi数据集的15 min交通速度预测任务中,STGCN模型的预测准确率比HA模型高了2.4%,比ARIMA模型高了25.8%,比SVR模型高了1.1%;T-GCN模型的预测准确率比HA模型高了3.5%,比ARIMA模型高了26.9%,比SVR模型高了2.2%; ST-AGTCN模型的预测准确率比HA模型高了6.0%,比ARIMA模型高了29.4%,比SVR模型高了4.7%。由于HA模型和ARIMA模型是在将交通速度假设为平稳的时间序列数据的前提下进行的交通预测,实际上这并不符合交通速度具有非线性、非平稳的特点,特别是当利用历史数据进行多步预测的时候,预测误差会累计传播。而SVR模型主要根据核函数思想,完成对输入输出关系之间的映射。这些方法都没有考虑到交通信息的空间相关性,难以处理具有复杂时空相关性的交通信息,因此,它们的预测效果差于基于深度学习方法的预测模型。
3)基于深度学习方法模型的评估:将STGCN、T-GCN、ST-AGTCN这3个预测模型进行比较,三者都利用了图卷积方法从交通数据中提取空间相关性特征。在空间维度上,STGCN和T-GCN都使用了一阶近似的GCN方法, ST-AGTCN模型使用切比雪夫多项式近似的GCN方法。在时间维度上,STGCN模型使用普通一维CNN处理,T-GCN模型使用GRU处理交通信息的时间相关性。如1.4节所述,使用CNN或者RNN的方法处理时序数据具有一定的局限性。ST-AGTCN模型通过增加注意力模块,根据输入数据构建出时空注意力矩阵;联合图卷积获取空间相关性特征,并通过门控时卷积方法捕获交通信息中的时间相关性特征。通过实验结果可知,在2个数据集上的15 min和30 min交通速度预测任务当中, ST-AGTCN的预测准确率高于STGCN和T-GCN。例如,在SZ-taxi数据集的15 min交通速度预测任务当中,ST-AGTCN的预测准确率比STGCN高3.6%,比T-GCN高2.5%。该实验结果表明了ST-AGTCN模型在挖掘交通信息的时空相关性特征方面具有优势。
4 总结
交通速度随着时间和路段的不同而不断变化,具有强烈的时空相关性、随机性、非线性等特点。针对这些问题,本文基于注意力机制和图卷积神经网络相结合的方法提出了ST-AGTCN模型,通过挖掘交通速度的时空相关性特征,提高交通速度预测准确率。实验结果表明,ST-AGTCN预测模型的准确率高于其他5个基准模型,在挖掘交通信息的时空相关性特征方面具有优势。该预测模型为交通管理和交通出行提供了科学依据。今后将进一步优化网络结构和参数设置,探究将ST-AGTCN模型应用于其他具有时空结构的预测场景,如社交网络预测、空气质量预测等现实场景。
参考文献
[1] MA X L,TAO Z M,WANG Y H,et al.Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J].Transportation Research Part C:Emerging Technologies,2015,54:187-197.
[2] FU R,ZHANG Z,LI L.Using LSTM and GRU neural network methods for traffic flow prediction[C]//Youth Academic Annual Conference of Chinese Association of Automation (YAC),IEEE,2016.
[3] 秦胜君,李婷.一种基于长短记忆模型的交通轨迹异常挖掘模型[J].广西科技大学学报,2021,32(2):58-64.
[4] 罗文慧,董宝田,王泽胜.基于 CNN-SVR 混合深度学习模型的短时交通流预测[J].交通运输系统工程与信息,2017,17(5):68-74.
[5] YU B,YIN H,ZHU Z.Spatio-temporal graph convolutional neural network:a deep learning framework for traffic forecasting[C]//Proceedings of the 27th International Joint Conference on Artificial Intelligence
(IJCAI),2018:3634-3640.
[6] VASWANI A,SHAZEER N,PARMAR N,et al.Attention is all you need[C]//31st Conference on Neural Information Processing Systems(NIPS),2017:5998-6008.
[7] FENG X C,GUO J,QIN B.Effective deep memory networks for distant supervised relation extraction[C]//Proceedings of the 26th International Joint Conference on Artificial Intelligence(IJCAI),2017:4002-4008.
[8] GUO S N,LIN Y F,FENG N,et al.Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[J].Proceedings of the AAAI Conference on Artificial Intelligence,2019:922-929.
[9] 朱宗洪,李春贵,李炜,等.改进Faster R-CNN模型的汽车喷油器阀座瑕疵检测算法[J].广西科技大学学报,2020,31(1):1-10.
[10] DEFFERRARD M,BRESSON X,VANDERGHEYNST P.Convolutional neural networks on graphs with fast localized spectral filtering[C]//30th Conference on Neural Information Processing Systems(NIPS),2016:3844-3852.
[11] HAMILTON W L,YING R,LESKOVEC J.Inductive representation learning on large graphs[C]//Conference on Neural Information Processing Systems(NIPS),2017:1024-1034.
[12] 朱凱利,朱海龙,刘靖宇,等.基于图卷积神经网络的交通流量预测[J].智能计算机与应用,2019,9(6):168-170,177.
[13] SIMONOVSKY M,KOMODAKIS N.Dynamic edge-conditioned filters in convolutional neural networks on graphs[C]//Conference on Computer Vision and Pattern Recognition(CVPR),2017:3693-3702.
[14] 袁华,陈泽濠.基于时间卷积神经网络的短时交通流预测算法[J].华南理工大学学报(自然科学版),2020,48(11):107-113,122.
[15] OORD A V D,DIELEMAN S,ZEN H,et al.WaveNet:a generative model for raw audio[EB/OL].arXiv:1609.03499,2016[2021-08-01].https://arxiv.org/abs/1609.03499v2.
[16] LIU J,GUAN W.A summary of traffic flow forecasting methods[J].Journal of Highway and Transportation Research and Development,2004,21(3):82-85.
[17] WILLIAMS B M,HOEL L A.Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: theoretical basis and empirical results[J].Journal of Transportation Engineering,2003,129(6):664-672.
[18] SMOLA A J,SCH?LKOPF B.A tutorial on support vector regression[J].Statistics and Computing,2004,14(3):199-222.
[19] ZHAO L,SONG Y J,ZHANG C,et al.T-GCN:a temporal graph convolutional network for traffic prediction[J].IEEE Transactions on Intelligent Transportation Systems,2020,21(9):3848-3858.
Attention-based spatio-temporal graph convolutional neural network for traffic speed prediction
HUANG Weijian, LI Chungui*
(School of Electrical, Electronic and Computer Science, Guangxi University of Science and Technology,
Liuzhou 545616, China)
Abstract: Traffic speed is an important indicator to measure the traffic state. Real-time and accurate traffic speed prediction is an important part of building an intelligent traffic system. Towards the problems of the randomness, nonlinearity and spatio-temporal correlation of traffic speed, a traffic speed prediction model is proposed by using the attention based spatio-temporal graph convolutional neural network. Firstly, the spatial and temporal attention weight matrix is constructed by using the attention mechanism, with the spatial correlation features of traffic information captured by combining with the graph convolution method. Secondly, the time correlation is obtained by gating time convolution. Finally, the proposed model and the other five benchmark models are tested on two public traffic speed data sets respectively. Experimental results show that the accuracy of the prediction model is 75.1% and 86.6% on the two data sets respectively, which is about 3% higher than the advanced benchmark models. It shows that the proposed model can provide important scientific basis for traffic control with its high accuracy and stability.
Key words: traffic speed prediction; attention mechanism; graph convolution; spatial-temporal correlation
(責任编辑:黎 娅)
