Study on Influence Law of System Parameters on the Dynamic Response of High-static-low-dynamic Stiffness Vibration Isolator Working Under Off-design Condition
2021-12-31-,-,,-
-,-,,-
(1.Xiamen Key Laboratory of Marine Corrosion and Smart Protective Materials,Marine Engineering Institute,Jimei University,Xiamen 361021,China;2.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiao Tong University,Shanghai 200240,China)
Abstract: A high-static-low-dynamic stiffness (HSLDS) vibration isolator using a circular plate as negative stiffness corrector and paralleling with linear spring is introduced in this paper.The buckling modes of the circular plate are analyzed by using FEM while the HSLDS characteristics of the vibration isolator are calculated and verified using ANSYS software.If the load is chosen properly,the equilibrium point will be set at the zero stiffness point, any change of the load will cause the equilibrium point to deviate from the initial setting equilibrium point. The nonlinear mathematical model of HSLDS vibration isolator considering load imperfection is developed and its response characteristics are analyzed by using the increment harmonic balance (IHB)method,and the influence law of the system parameters on it is analyzed. The results show that the dynamic response will exhibit softening,hardening, and softening-to-hardening characteristics, depending on the effect of load imperfection,damper and excitation force.
Key words:high-static-low-dynamic;vibration isolator;off-design condition;FEM
0 Introduction
There always exist strong vibrations in marine equipment with rotating elements, which may cause fatigue damage to the equipment performance, or may reduce the reliability of operation and the accuracy of measurement,increasing the navigation risk.The passive isolation technology is the most common approach to attenuate the unwanted vibrations. However, the traditional linear isolator encounters the difficulty between the low resonance frequency and the large static deformation by reducing the stiffness with the same mass of the system.In recent years,high-static-low-dynamic stiffness (HSLDS)isolator systems have been introduced to overcome this disadvantage.The negative stiffness structure is parallelly connected with a linear isolator to form an HSLDS nonlinear isolator. Carrela et al[1-3]used two inclined springs to produce negative stiffness to counteract the positive stiffness provided by the vertical spring and studied both the force transmissibility and displacement transmissibility of the isolator. Other means of negative stiffness include cam-rollerspring mechanism (CRSM)[4], bi-stable structures[5], magnetic springs[6], and scissor-like structures[7-8]. The review paper by Ibrahim[9]compares many nonlinear isolators and shows that research in nonlinear isolators is a very active field. From the reviews above, if the negative stiffness mechanism is chosen carefully, the combined nonlinear isolator can exhibit quasi-zero stiffness at the equilibrium point with the rated load. However, it is very difficult to consider whether the working position at the desired equilibrium point in reality is in under-loaded or overloaded condition.With the load changing,the equilibrium point will deviate from the setting point.Huang and Liu[10~12]studied the effect of the system imperfections on the dynamic response of a high-static-low-dynamic stiffness vibration isolator using the compressed Euler beams as the negative stiffness mechanism.Meng et al[13]theoretically designed and analyzed the characteristics of a quasi-zero stiffness isolator using a disk spring as negative stiffness element, considering the overloaded or under-loaded conditions. However, there are few papers reporting the designing of the HLSDS isolator using a buckling circular plate as negative stiffness corrector. Moreover, researching the effect of different system parameters on the HLSDS isolator working under off-design condition is necessary for evaluation of the isolation performance in reality.
In this paper,the simple structure of an HSLDS vibration isolator using buckling mode of a circular plate as the negative stiffness mechanism is firstly presented. Then the buckling mode of the circular plate is analyzed using FEM while the HSLDS characteristics of the vibration isolator are calculated and verified by using ANSYS software.And thirdly,the nonlinear mathematical model of the HSLDS vibration isolator considering overloaded or under-loaded imperfection is developed and its response characteristics are analyzed by using the increment harmonic balance (IHB) method, followed by analysis of the influence law of the system parameters on the dynamic response of the isolator.
1 Structure of vibration isolator with HSLDS
It is required to develop HSLD stiffness isolators with minimum number of elements, preferably with only one that provides the best simplicity, and high reliability. The structure of an HSLDS vibration isolator is shown in Fig.1. The isolator consists of a pre-stressed buckling circular plate and a linear spring. The pre-stressed buckling circular plate acts as the negative stiffness while the linear spring acts as the positive stiffness. The HSLD stiffness is obtained by connecting the circular plate and the linear spring in parallel while the weight of the isolated object is sustained by the linear spring. The structure of the designed vibration isolator is simple and reliable.
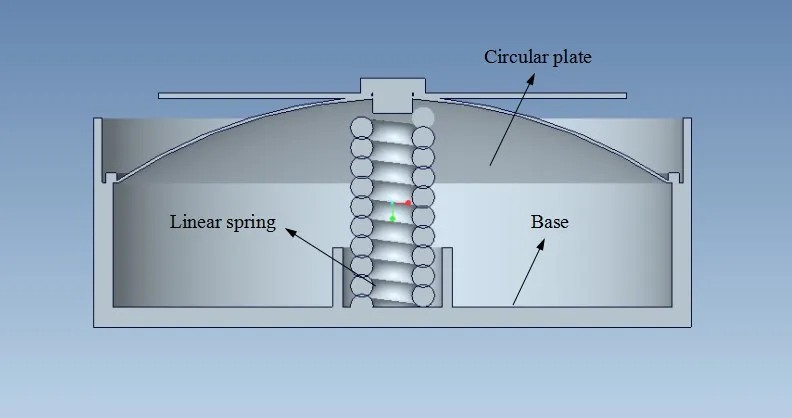
Fig.1 Structure of HSLDS vibration isolator
2 FEM analysis of HSLDS vibration isolator
2.1 FEM analysis of the buckling modes of circulate plate
The buckling modes of the circulate plate can be calculated by using the FEM. They can give the initial disturbances to the plate for calculating the nonlinear buckling analysis which can verify the HSLDS characteristics of the vibration isolator. The FEM model of circular plate with parameters ofR=260 mm,t=1 mm,E=200 GPa,ν=0.3 are built by using ANSYS software. Moreover, the boundary condition of circular plate periphery is supposed with a simple support. The first and second steps of the buckling modes of the circulate plate are shown in Fig.2 and Fig.3 respectively.

Fig.2 First step of buckling mode of circular plate

Fig.3 Second step of buckling mode of circular plate
It can be seen that the first step of the buckling mode value isPr1=141 801 Pa and the second step of buckling mode value isPr2=468 156 Pa. The fist buckling mode of the circular plate can be used to initialize the outline of circulate plate to verify the HSLDS characteristics of the designed isolator.
2.2 FEM analysis of the HSLDS characteristics of the vibration isolator
In order to verify the HSLDS characteristics of the vibration isolator shown in Fig.1, the FEM model of the isolator has been built by using the ANSYS software as shown in Fig.4.The parameters of the circular plate are the same as those in Section 3.1,and the stiffness of a linear spring connecting to the circular plate isk=10 N/mm. The boundary condition of circular plate is simple support and the base of linear spring is restrained. The first step of the buckling mode of the circular plate shown in Fig.2 is used to form the outline of circular plate for the nonlinear buckling analysis, in which the arch height of the center of the circular plate is about 8.7 mm.The center of the circular plate is applied with a static force ofF=1 000 N.The results of the nonlinear buckling analysis are shown in Figs.5-6.It is shown in Fig.5 that the displacement is increasing while the force remains unchanged.Accordingly, there is an area with stiffness close to zero as shown in Fig.6. Moreover, it can be seen from the figures that the force is about cubic displacement and the stiffness is about quadratic displacement. The structure of the vibration isolator designed in this paper has been verified with HSLD stiffness on the force characteristics. It would have great potential in vibration isolation as it is easy and reliable in application.
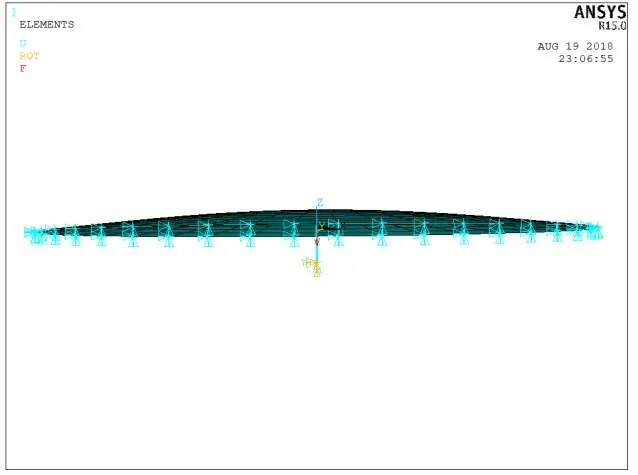
Fig.4 FEM model of vibration isolator
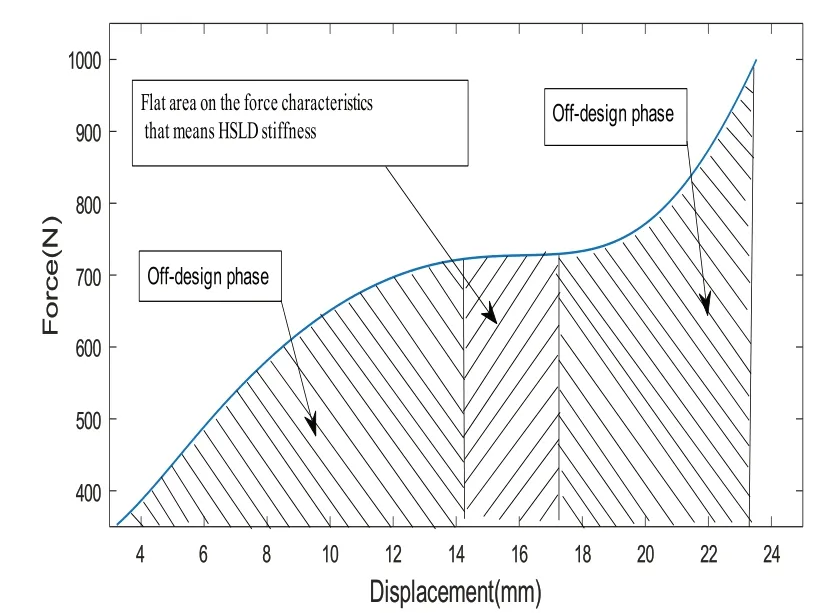
Fig.5 Relationship between the force and displacement of isolator

Fig.6 Relationship between the stiffness and displacement of isolator
3 Amplitude-frequency characteristics of the HSLDS vibration isolator working under the off-design condition
3.1 HSLDS vibration isolator working under off-design condition
If an HSLDS isolator works under the rated load,the negative stiffness of the buckling circular plate will cancel out the positive stiffness of the linear spring,it exhibits quasi-zero stiffness characteristics as shown in Fig.7. However, as mentioned above,it is difficult to assure the load to be balanced at the initial setting equilibrium point in reality. The vibration isolator working under off-design condition discussed in this paper is just considered with load imperfection without stiffness imperfection. It means that negative stiffness still cancels out positive stiffness, but the equilibrium position deviates from the initial setting equilibrium position due to overload or underload,as shown in Figs.8-9.

Fig.7 HSLDS isolator with rated load condition
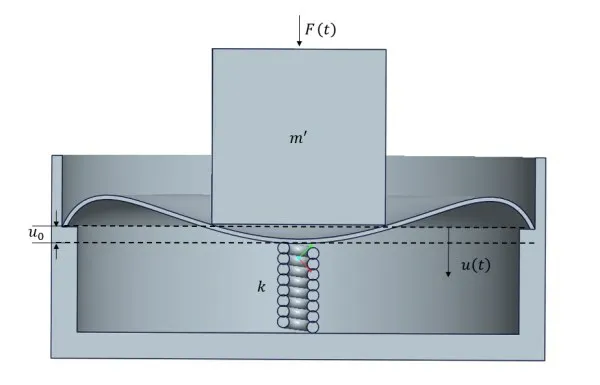
Fig.8 HSLDS isolator with overload
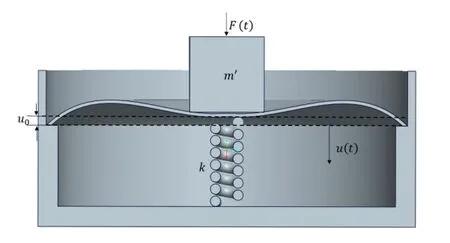
Fig.9 HSLDS isolator with underload
3.2 Amplitude-frequency characteristics of the isolator working under off-design condition
The HSLDS vibration isolator can be simplified as one-degree-freedom vibration isolation system with the nonlinear elastic restoring force as shown in Fig.10, which is different from the linear isolator system. As shown in Fig.5, the relationship between force and displacement is cubic, the elastic force of the HSLDS isolator can be written as follows:


Fig.10 Simplified system for HSLDS vibration isolator
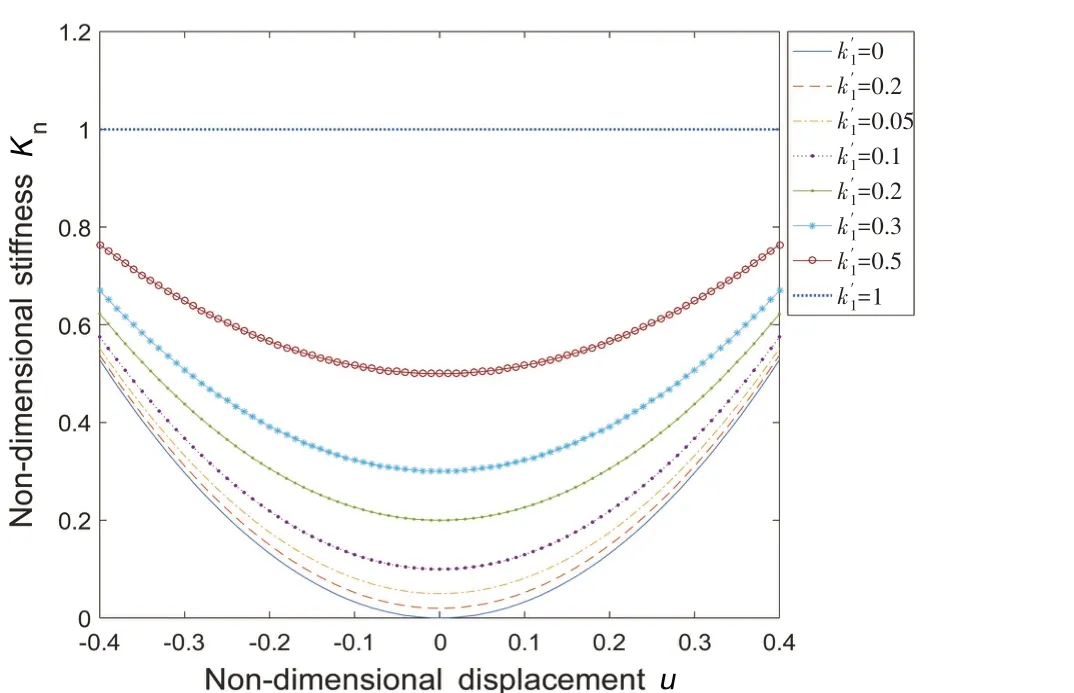
Fig.11 Non-dimensional stiffness of the HLSDS isolator for different k′1

When the system suffers from the harmonic excitation forceF=F0cosωt, the dynamic equation of the system can be written as the Duffing equation:
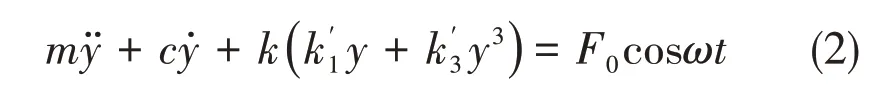
wheremandcdenote the load mass and damper respectively.For simplicity in the mathematical formulation, the following dimensionless parameters are introduced:


whereA0andA1are the response amplitudes of constant item and harmonic item respectively,andθis the phase angle.Substituting Eq.(8)into Eq.(7),the equations can be obtained by using the increment harmonic balance(IHB)method as follows:

3.3 Effects of the system parameters on the responses of the isolator working under off-design condition
The isolator working under off-design condition discussed in this paper referrs to only load imperfection which means the vibration isolator working for overload or underload,namely the equilibrium position deviating from the initial setting equilibrium position, the stiffness of the linear isolator just cancelling out the negative stiffness of the negative stiffness corrector, and the dimensionless stiffness coefficientk′1of the HSLDS isolator being zero.In other words,the effect of the system parameters on the dynamic response is investigated for a quasi-zero stiffness isolator.


Fig.12 Response amplitude items(A0,A1)of the HSLDS isolator with f0=1×10-3 and ζ=0.01 for different u~ 0(u~ 0=0,0.01,0.03,0.05)and (=0.3,0.6,0.8)
The response amplitude items (A0,A1) of the HSLDS isolator with differentu~0andf0are shown in Fig.13. It can be seen that the response amplitude exhibits the hardening characteristics when the isolator works at the initial setting equilibrium point (u~0=0) with the rated load. Moreover the harmonic itemA1and the resonance frequency are increasing as the excitation force level rises.With the overload,the system exhibits softening,softening-to-hardening characteristics as the excitation force level rises.
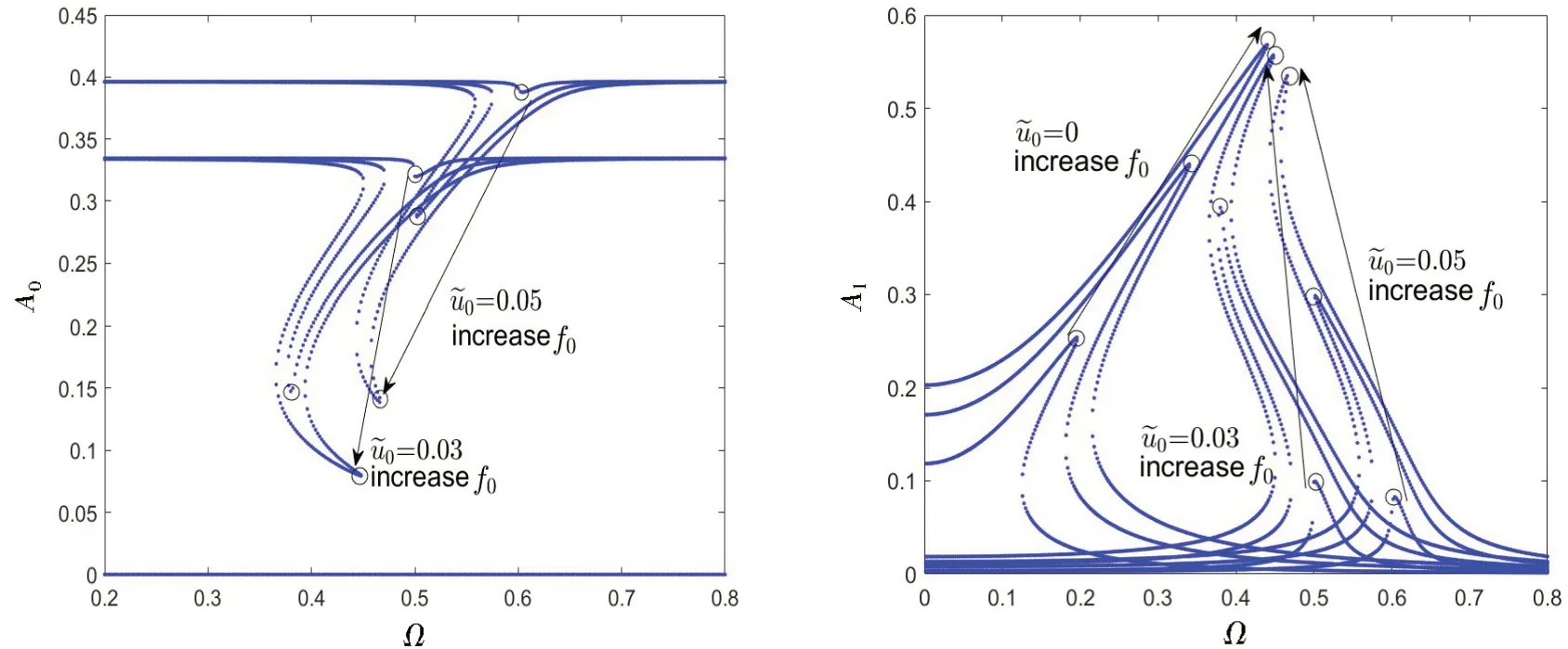
Fig.13 Response amplitude items(A0,A1)of the HSLDS isolator with k′3=0.8 and ζ=0.01 for different u~ 0(u~ 0=0,0.03,0.05)and f0(f0=1×10-3,3×10-3,5×10-3)
The response amplitude items (A0,A1) of the HSLDS isolator with differentu~0andζare shown in Fig.14.It can be seen that the response amplitude exhibits the same as that in Fig.13.The reason is that the dimensionless damping coefficientζacts like the excitation force levelf0, while it may have the opposite effect.
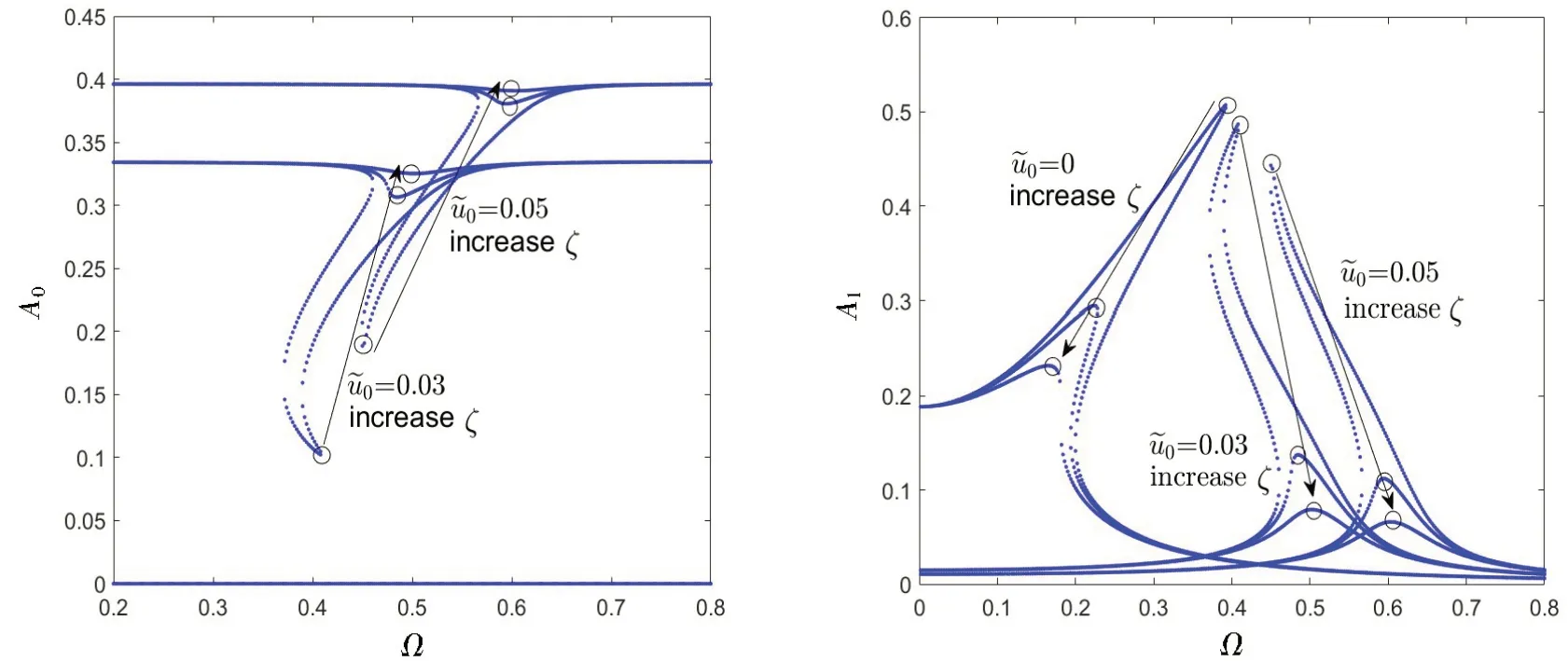
Fig.14 Response amplitude items(A0,A1)of the HSLDS isolator with k′3=0.8 and f0=3×10-3 for different u~ 0(u~ 0=0,0.03,0.05)and ζ(ζ=0.01,0.03,0.05)

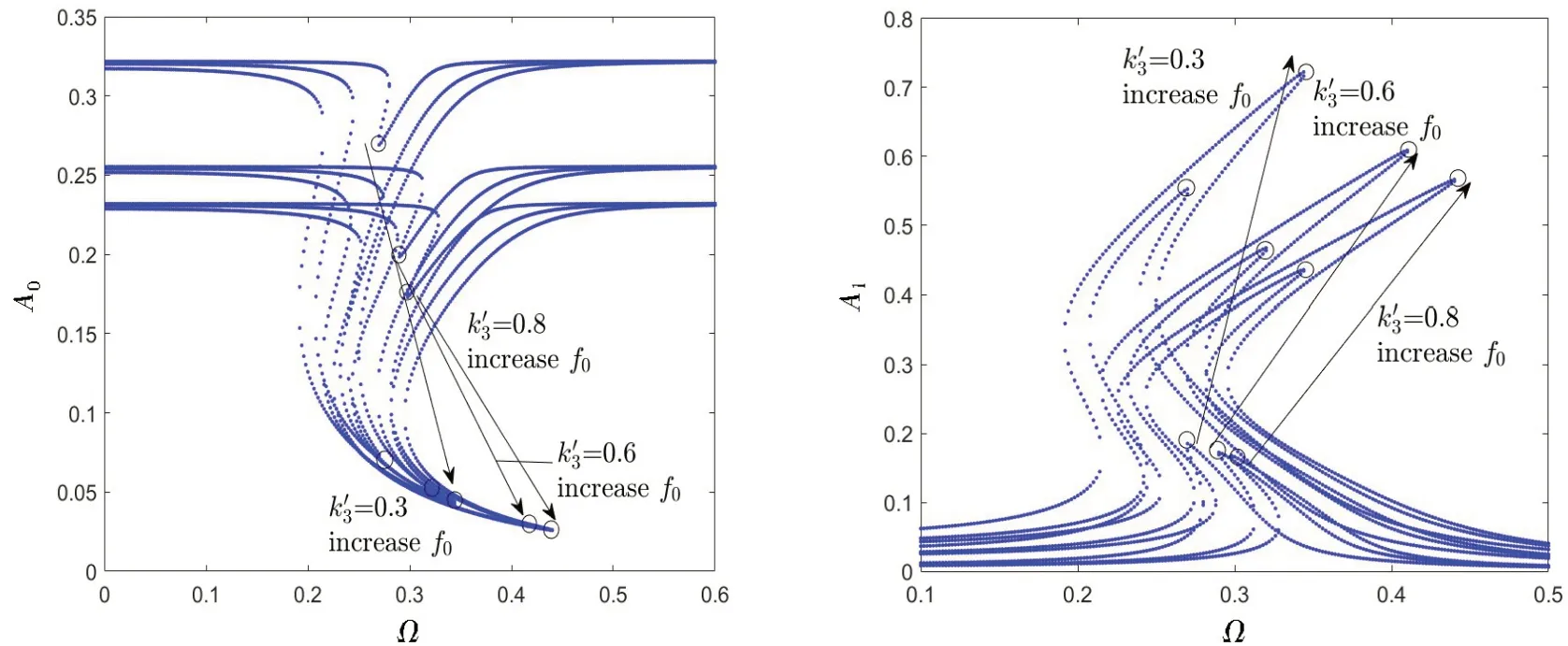
Fig.15 Response amplitude items(A0,A1)of the HSLDS isolator with u~ 0=0.01 and ζ=0.01 for different k′3(k′3=0.3,0.6,0.8)and f0(f0=1×10-3,3×10-3,5×10-3)
4 Conclusions
With a novel HSLDS vibration isolator using the circular plate as negative stiffness corrector proposed,the effects of the system parameters on the response of the isolator working under off-design condition are discussed. The results show that the overload and excitation force can make the resonance frequency of the HSLDS isolator higher, the vibration isolation frequency band narrow,and the vibration isolation effect worse.The system exhibits softening,hardening,and softening-tohardening characteristics as the excitation force level rises or the system works under overload.The damper acts like the excitation force while it may have the opposite effect. Decreasingcan make the resonance frequency lower, but the response amplitude items (A0,A1) are increasing. Although the HSLDS isolator works under the overload condition, it can also exhibit its excellent low-frequency vibration isolation property with small excitation force.
杂志排行
船舶力学的其它文章
- Responses of Large-ship Mooring Forces Based on Actual Measurement
- Experimental Study on Fatigue Crack Growth of Compact Tensile Specimens Under Two-Step Variable Amplitude Loads with Different Cyclic Ratios
- Bivariate Kernel Density Estimation for Meta-ocean Contour Lines of Extreme Sea States
- Study on the Tip Vortex Control Effect and Rule of Pump Jet Thruster by Groove Structure
- On Scale Effect of Open Water Performance of Puller Podded Propulsors Based on RANS
- Main Engine Power Prediction for Large Vessels Based on Gaussian Mixture Model and Deep Neural Network
