On Scale Effect of Open Water Performance of Puller Podded Propulsors Based on RANS

,-,-,-,

(1.Departments of Naval Architecture,Ocean and Structural Engineering,School of Transportation,Wuhan University of Technology,Wuhan 430063,China;2.Wuhan Marine Electric Propulsion Research Institute,Wuhan 430064,China)

Abstract: Podded electric propulsors are widely used for scientific research vessels, naval ships and merchant ships due to their advantages in high modularity, environmental protection, great maneuverability, low noise, etc.. The hydrodynamic characteristics of the podded propulsors are often analyzed based on the numerical simulation and/or experimental test in model scale. However, the complicated configuration of the podded propulsors imposes limitations on the extrapolation of the model-scale data to full-scale results.The current study focuses on the scale effect of the open-water performance of a puller podded propulsor based on RANS method. The open-water performance of the puller podded propulsor is numerically simulated by using the Rayleigh-Averaged Navier-Stokes (RANS)method together with a two-equation turbulence model. The scaling laws of the pressure force, frictional force and total force of different components are separately analyzed based on the calculated open-water characteristics of the puller podded propulsor with different sizes.A correction method focusing on the scale effect of the frictional drag of non-rotating components is then proposed and verified by comparing the RANS results and the extrapolated drag from the model scale to larger scales.

Key words:puller podded propulsor;scale effect;RANS method;open-water performance

0 Introduction

Podded electric propulsors are a new type marine electric propulsion system,which has recently become popular in the practical engineering due to its advantages in high modularity, environmental protection, great maneuverability, low noise, etc.. Podded electric propulsors are widely used for scientific research vessels, military ships and merchant ships, such as ocean research ships,polar icebreakers,large cruise ships,ro-ro ships,landing craft and destroyers. A lot of investigations have been carried out for the hydrodynamics of the podded propulsors that are applied in various fields. However, both of experimental tests and numerical simulations are often conducted in model scale.It is therefore of great importance to analyze the scale effect of podded propulsors in order to predict the hydrodynamic performance of full-scale podded propulsors based on the model scale data.

Many institutes like HSVA(Germany),VTT(Finland)and MARIN(the Netherlands)have conducted experimental studies on the scale effect of podded propulsors.It is suggested that the complicated configuration of a podded electric propulsor, normally consisting of the pod, strut and propeller, imposes limitations on the extrapolation from model scale to full scale by following the scaling method of traditional propellers.The numerical simulation of a podded propulsor can be carried out based on the potential flow theory and/or the viscous flow theory. Potential flow theory is generally used for preliminary design due to its high computational efficiency while the viscous flow method is often used for the study of the scale effect because it can capture more flow details. The RANS method is widely used because of its higher calculation efficiency and fair accuracy. Choi (2014)[1]studied the scale effect of a puller podded propulsor based on the RANS method. It was shown that the performance of the propeller blade was mainly related to the advance coefficient with less scale effect, while the non-rotating components (such as the pod and the strut) had a larger scale effect because the frictional drag was highly related to the Reynolds number. Park (2014)[2]also studied the hydrodynamic performance of a puller podded propulsor based on RANS method,in which a parameter of drag velocity ratio was proposed to extrapolate the model scale data to the full scale performance of the pod and the strut.The drag velocity ratio was suggested to be affected by the propeller load and the Reynolds number.

The existing correction methods for the scale effect of the podded propulsors mainly include the method that was introduced at the 25th ITTC (2008)[3]and theβcoefficient method[4]. A semiempirical method was presented at the 25th ITTC (2008) for prediction of the pod housing drag by using the form factor approach.The form factors for the pod and the strut can be calculated by simple empirical formulas according to their geometry properties.However,there are several correction factors which should be determined by experience,and their applicability on different pod types remains to be discussed. The Russian Krylov Ship Institute presented aβcoefficient method to correct the scale effect, where theβcoefficient was independent of the advance coefficient. However,theβcoefficient would be influenced by the size, advance coefficient and the geometry of the nonrotating components.It is still a challenge to establish a general correction method.

The scaling law of the open-water performance of puller podded propulsors has been studied based on the RANS method in the current study.It mainly focuses on the scale effect of the non-rotating components of puller podded propulsors by separately examining the variation of the pressure drag,frictional drag and total drag of each component with the size and the Reynolds number.A correction method for the scale effect on the open-water performance of puller podded propulsors is finally proposed and verified according to the RANS results for puller podded propulsors at different scales.

1 Numerical method

The numerical calculation of the open water performance of a puller podded propulsor is carried out by using the Rayleigh-Averaged Navier-Stokes (RANS) method together with the realizablek-εturbulence model.

1.1 Governing equations

The governing equations are written for the mass and momentum conservation of the fluid around the puller podded propulsor.The effect of turbulence on the mean flow properties is investigated by decomposing the flow properties into a mean component and a time-dependent fluctuating component.The mass and momentum conservation equations can then be rewritten as follows:

1.2 Turbulence modeling

The turbulence model is important to make the equation closed due to additional terms of Reynolds stress terms in the governing equations. The current study adopts the widely-used twoequation turbulence models based on the Boussinesq approximation (Eq.(3)). The eddy viscosity model can give relatively reasonable results for the numerical calculation of the general practical flow problem. In the current study, the realizablek-εturbulence model is selected to close the RANS equations, which was validated in previous work (Yang, 2019[5]) and was also recommended in several published works(Burg,2005[6];Choi,2014[1];Ilieva,2015[7]).

whereμtis the coefficient of the turbulent viscosity(N·s/m2),andkis turbulent kinetic energy.

1.3 Treatment of rotational motion

The multi-motion reference frame model(MRF)and the sliding mesh(SM)model are commonly used to deal with the rotational motion in the numerical simulation of propulsors. Compared with MRF, the grid nodes of SM will move and try to adapt to the rotational motion, which is more suitable for unsteady simulations and/or complicated systems. In the current study, the SM method is adopted to simulate the interaction between the moving components and the flow field.

2 Validation

To validate the numerical model for the open-water performance prediction of puller podded propellers,a propulsor is firstly selected and simulated by using the above-mentioned RANS method. The results are compared with those from the experimental tests conducted in Shanghai Ship and Shipping Research Institute(SSSRI).

2.1 Geometry description

The puller podded propulsor studied in this section is composed of a propeller, a pod, a strut and a fin, as shown in Fig.1. The typical parameters of the puller podded propulsor are shown in Tab.1.

Fig.1 Geometry modeling of the puller podded propulsor

Tab.1 Typical parameters of the puller podded propulsor

2.2 Computational domain and meshing

The entire computing domain is a cylinder domain with a diameter of 7D.It is extended to 13Din the central axial direction, starting at 5Dupstream from the propeller plane and ending at 8Ddownstream behind the propeller plane. The computational domain is divided into a stationary domain and a rotating domain, in which the data are exchanged through the interface, as shown in Fig.2. The boundary condition of the inlet is set as the velocity inlet. The outlet is set as the pressure outlet condition.The side of the cylinder is set as symmetry plane.The no-slip wall conditions are applied on the wall boundaries, including the pod body surface, the propeller blades, the fin,and the strut surface.

The trimmer meshing is adopted for the discretization of whole domain,whereas the prism layer meshing is used to simulate the boundary layer.At the same time,the components of the podded propulsor are partially encrypted,and the height of the first layer is guaranteed to ensure they+values of the no-slip wall in the current study are mostly kept in the range of 30 to 300, as shown in Fig.3. For different scales of podded propulsors, the base sizes of the mesh generation are varied with the scale changing.Especially,the near-wall meshes are adjusted via try and error to keep they+in a reasonable range.The properties of the grids at different scales are stated in Tab.2,including the number, thickness and growth rate (Rate) of the prismatic layer and the base size of different scales.

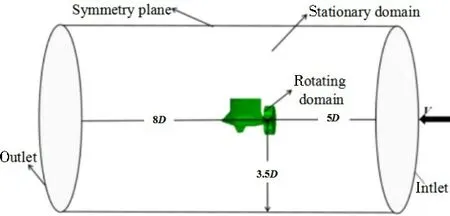
Fig.2 Computational domain for the numerical simulation

Fig.3 Close-up of the meshing scheme

Tab.2 Grid schemes of different scales

2.3 Results and analysis

The analysis of the open-water performance of the puller podded propulsor demands further definitions of the characteristic parameters of different components, including the propeller, pod and strut.To facilitate subsequent work,relevant parameters are defined as follows:

whereT,TP,RPODandRSTRUTseparately represent the thrust/drag of the overall podded propulsor,the propeller,the pod and the strut;VArepresents the advance velocity at inlet;ρrepresents the density of fluid;Qrepresents the propeller torque;nrepresents the propeller revolution speed;Drepresents the diameter of propeller.

2.3.1 Grid sensitivity

The grid sensitivity is demanded to be examined for the puller podded propulsor at different scales. Firstly, for the case of model scale (λ=1), three sets of geometrically similar grids are generated and tested, the corresponding results are given in Tab.4 and Fig.4. It can be observed that, under the working condition ofJ=0.5, the hydrodynamic performance show a monotonic convergence (0＜Rk＜1) with the mesh number increasing, where the convergence ratios (Rk) are calculated according to the ITTCQuality Manual (1999). As shown in Fig.4, for most of working conditions, the propulsors’hydrodynamic performance almost remains the same with the mesh number increasing, indicating that the current density of the grid is sufficient.

Fig.4 Comparison of open water performance of the podded propulsor of the three sets of grids

Tab.3 Grid features for the test case of λ=1

Tab.4 Hydrodynamic performance of three sets of grids(J=0.5)

2.3.2 Results of CFD and EFD

The medium density grids are selected for the following simulations of the puller podded propulsor. The numerical results are compared with the experimental ones, as shown in Fig.5.It can be observed that the calculated thrust,torque and efficiency are in good agreement with the experimental results, with errors of less than 4.5%.

Fig.5 Comparison of open water performance of the podded propulsor between numerical calculation and experimental test

3 Analysis of scale effects

By using the above-validated numerical models, the scale effects on the open-water performance of the puller podded propulsors have been investigated according to the numerical simulations of the puller podded propulsors with different sizes.The geometry of the puller podded propulsor has been modified for simplification (as shown in Fig.6), where the fin is removed, and the strut is streamlined but with the same parameters as the original geometry. The scale effect of the puller podded propulsor is explored by examining the forces on the propeller and non-rotating components at different scales,respectively.The calculation conditions are determined by geometric similarity, advance coefficient similarity, and Froude number similarity with the Reynolds number larger than the critical Reynolds number. The corresponding diameter of the propeller is varied from 0.2 m to 1.2 m. The revolution speed and the corresponding Reynolds number of the puller podded propeller with different sizes and advance coefficients are shown in Tab.5.

Fig.6 Geometry modeling of the modified puller podded propulsor

The open-water performance of the puller podded propulsor involves not only the contribution of the propeller,but also the contribution of the non-rotating components like the pod and the strut.It is therefore necessary to consider the effect of the non-rotating components on the scale effect of the open-water puller podded propulsor. In the current study, the scale effect of the puller podded propulsor has been assorted into two categories:the scale effect of the propeller and the scale effect of the non-rotating components.

3.1 Scale effects on the hydrodynamic performance of the propeller

The scale effect associated with the propeller of the puller podded propulsor has been considered in the similar way as the traditional propeller. The 25th ITTC (2008) mentioned that the scale effect of the propeller of the podded propulsor can be corrected by the correction method for the scale effect of conventional propellers provided by 15th ITTC(1978).

The torque and the thrust of the propeller of the puller podded propulsor at different scales are shown in Fig.7.It can be seen that the variation of the torque and thrust coefficients of the propeller of the puller podded propulsor is small as the size of the propeller increases.

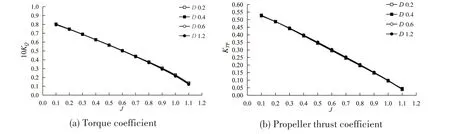
Fig.7 Open-water performance of the propeller of the puller podded propulsor at different scales

The forces on the propeller are then divided into the pressure force (with subscript p) and the frictional force(with subscript f)for further analysis.The definitions are as follows:

Fig.8 and Fig.9 show the torque and thrust of the propeller of the puller podded propulsor at different scales related to the pressure force and the frictional force,respectively.It can be observed that with the increase of the propeller size and the gradually-increased Reynolds number, the change of the torque and thrust coefficients related to the pressure force is very small, while those related to the frictional force decrease gradually. However, the proportion of the frictional force in the total force is small, resulting in a relatively limited influence on the overall scale effect of the propeller,as shown in Fig.7.It can be summarized that the scale effect on the hydrodynamic performance of the propeller of the puller podded propulsor is very small, the scale effects related to the frictional force appears to be larger than that related to the pressure force.

Fig.8 Torque coefficient of the propeller of the puller podded propulsor KQ atdifferent scales due to different forces

Fig.9 Thrust coefficient of the propeller of the puller podded propulsor KTP at different scales due to different forces

3.2 Scale effects on the hydrodynamic performance of non-rotating components

The scale effect associated with the non-rotating components, such as the pod and the strut,which generally generate drag rather than thrust,should be studied by specific methods that will be discussed in the subsequent section. Similarly, the drag of the pod and strut are also divided into the pressure drag (with subscript p)and the frictional drag (with subscript f),as shown in Eqs.(12)-(13).

whereRrepresents the drag;Crepresents the drag coefficient; and subscripts of POD and STRUT separately mean the values corresponding to the pod and the strut.

The drag coefficients of the pod and the strut of the puller podded propulsor at different scales are shown in Fig.10.The drag coefficients related to the pressure force and the frictional force of the pod and the strut of the puller podded propulsor at different scales are shown in Fig.11 and Fig.12,respectively.

The results show that both drag coefficients of the pod and the strut decrease as the propeller size increases.From the resolved drag results,it can be observed that,for the puller podded propulsor at different scales, the differences of the pressure drag coefficients of the pod and the strut are very small, while the frictional drag coefficients of the pod and the strut show more obvious variations. The overall scale effect will be affected by the proportion of the frictional drag accounting for the total drag.The scale effect of the non-rotation components of the puller podded propulsor therefore appears to be larger than that of the propeller,and the scale effect of the strut is larger than that of the pod as the frictional drag of the strut accounts for more than 40%of the total drag.

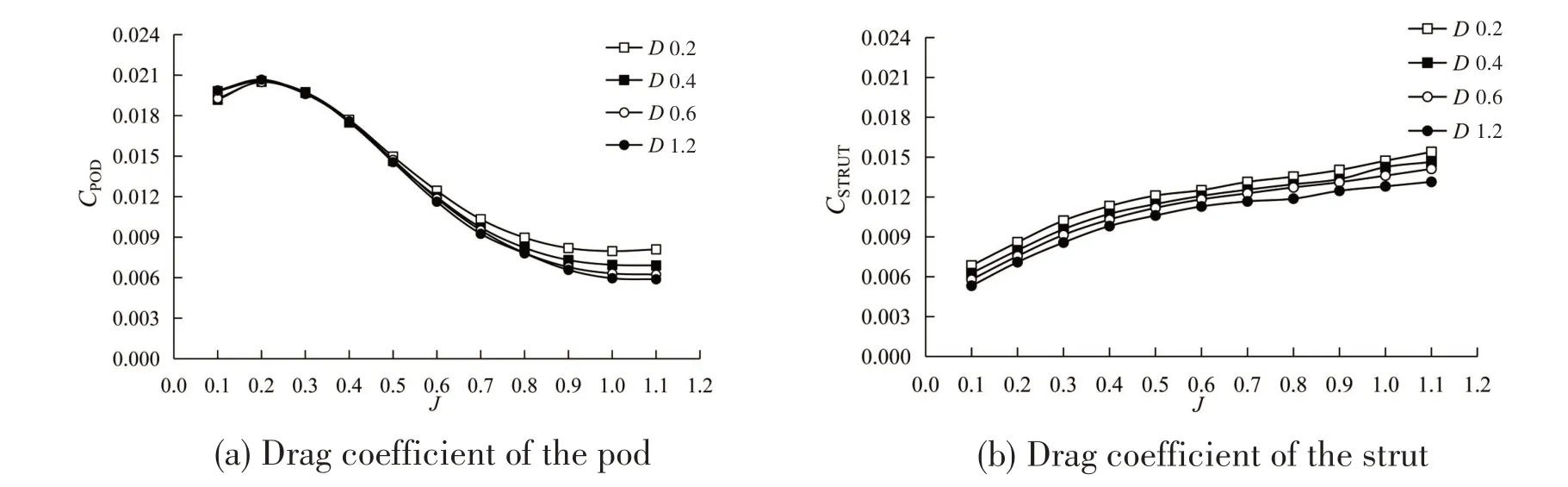
Fig.10 Drag coefficients of the pod and the strut of the puller podded propulsor at different scales

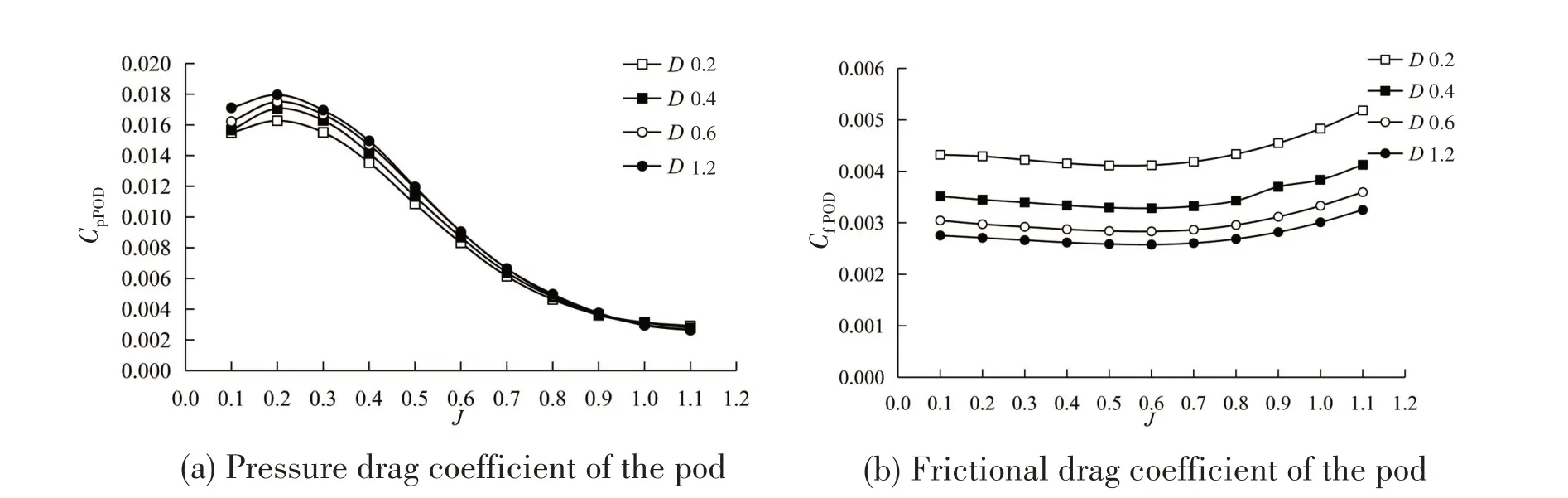
Fig.11 Drag coefficient of the pod of the puller podded propulsor CPOD at different scales due to different forces

Fig.12 Drag coefficient of the strut of the puller podded propulsor CSTRUT at different scales due to different forces

The scale effect related to each component can be summarized as:

(1)The scale effect related to the pressure drag of each component is small,while the scale effect related to the frictional drag of each component is more obvious.

(2) The overall scale effect of each component can be related to the proportion of frictional force in the total force. The scale effect of the propeller is very small because the pressure force is dominant in the total force,while the scale effect of the non-rotating components is larger than that of the propeller because the frictional drag becomes more important for the pod and strut,especially under the condition with high advance coefficients.

4 Correction method

According to the above analyses of the scale effects on the hydrodynamic performance of puller podded propulsor, it is suggested that a reasonable correction method requires different scaling laws for different components of the puller podded propulsor.The scale effect related to the frictional drag of the non-rotating components should be a major consideration.

4.1 Correction for the propeller of the puller podded propulsor

The propeller torque and thrust coefficients of full scale podded propulsors can be extrapolated from the value of model scale by the formula presented in the 15th ITTC(1978 ITTC formulae):

whereP/Dis the blade pitch diameter ratio at radius of 0.75R,b/Dis the ratio of blade chord length and diameter at radius of 0.75R,Zis the blade number,ΔCDis the blade drag coefficient difference between model scale and full scale,subscripts of S and M separately mean the values corresponding to the full scale and the model scale.

The open-water characteristics of the propeller with a diameter ofD=1.2(λ=6)under different advance coefficients are extrapolated from those of the propeller with a diameter ofD=0.2 (λ=1) by using the 1978 ITTC formulae. The extrapolated torque and thrust coefficients are then compared with the RANS results, as shown in Tab.6, where‘RANS’indicates the data calculated by the RANS method,‘1978 ITTC’indicates the data obtained by extrapolation through the 1978 ITTC formulae, and‘Error’can be expressed asError=(1978 ITTC-RANS)/RANS. It is shown that the differences between the RANS results and the 1978 ITTC results are small with errors less than 5%in most conditions, indicating that the 1978 ITTC formulae can be used for the correction of the scale effects on the propeller open-water performance of the puller podded propulsor.

Tab.6 Comparison of the open water performance of propeller

4.2 Correction for non-rotating components of the puller podded propulsor

According to the analyses of Figs.10-12, the preliminary correction method for the scale effects on the hydrodynamic performance of the non-rotating components is proposed: the pressure drag of each component can be extrapolated directly from the model scale to the full scale without considering the scale effects, whereas the frictional drag of each component related to the Reynolds number is assumed to be capable of being expressed and corrected by the formula presented in the 8th ITTC(1957 ITTC formula):

To validate the above assumption, the forces of non-rotating components of the puller podded propulsor are non-dimensionalized by usingρV2Sinstead ofρn2D4in this section, it can also eliminate the influence of the wetted surface area of different components on the subsequent analyses of scale effect. The pressure drag coefficients and frictional drag coefficients of the pod and strut are separately re-defined as follows:

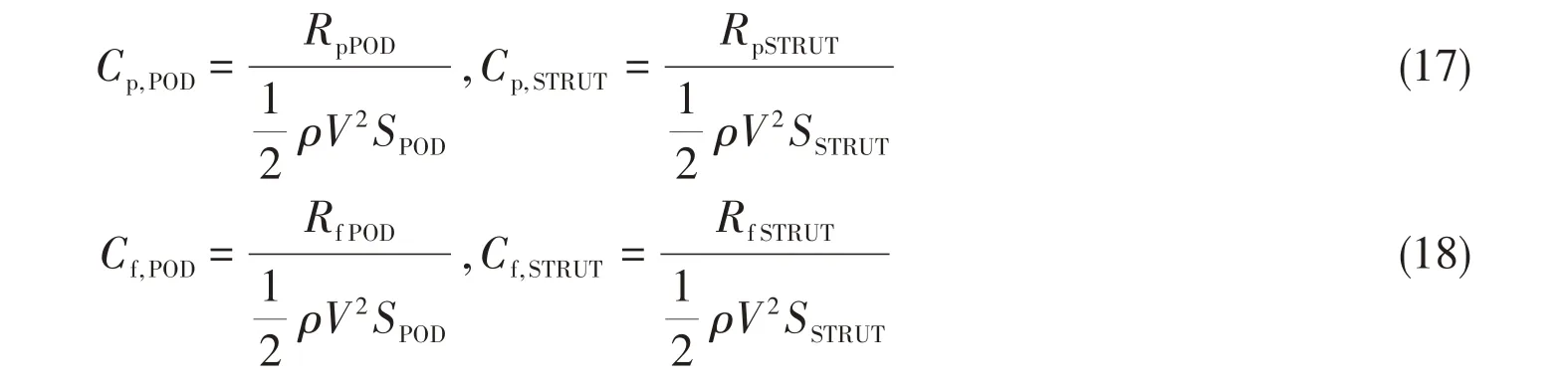
whereSis the wetted surface area of component referred,Vis the inlet velocity.

Fig.13 shows the pressure drag coefficients of the pod and the strut that are calculated by Eq.(17) for the podded propulsors at different scales. It can be seen that the scale effect related to the pressure drag of the pod and the strut is very small.It seems to be reasonable to ignore the scale effect related to the pressure drag of the pod and the strut.

Fig.13 Pressure drag coefficients of the pod and the strut of the puller podded propulsor at different scales by adopting the new dimensionless processing method

Fig.14 gives the frictional drag coefficients of the pod and the strut of the podded propulsor with different scales that are calculated by Eq.(18)versus the Reynolds numbers that are calculated by the following equation:

whereνis the kinematic viscosity,LandBare the characteristic lengths of different components,the longitudinal length and chord length are separately selected for pod and strut.

Fig.14 Frictional drag coefficients of the pod and the strut of the puller podded propulsor at different scales by adopting the new dimensionless processing method

In Fig.14, the frictional drag coefficients of each component calculated by Eq.(16) are also plotted for comparison. It can be found that the frictional drag coefficients of the pod and the strut decrease as the Reynolds number increases for the podded propulsor at the same working condition.The contour of the advance coefficient (dotted lines) indicates that the frictional drag coefficients of the pod and the strut increase as the advance coefficient decreases for the podded propulsor of the same size.More importantly,it clearly indicates that the frictional drag coefficient of the non-rotating components of the puller podded propulsor cannot be simply correlated to the inlet-velocity based Reynolds number,as what was stated in the 1957 ITTC formula,thus the assumed correction method is obviously inadequate.This may be caused by the interaction of various components of the podded propulsor, more specifically, the propeller induction effect is supposed to significantly affect the flow velocity in front of the pod and the strut. Therefore, the reasonable correction of the frictional drag requires an appropriate definition of the Reynolds number for the non-rotating components, including the determination of the characteristic length and the determination of the characteristic velocity of the pod and the strut.

(1)Determination of the characteristic length

It is suggested that the scale effect related to the frictional drag of the non-rotating components of the podded propulsor can be studied by examining the drag of the bare pod body(including the pod and strut) in order to weaken the influence of the interference among different components.In the current study, the drags of the bare pod body at different scales are firstly calculated by the RANS method, and the frictional drag are non-dimensionalized based onρV2Sfollowing Eq.(18).Then, the characteristic lengths of the pod and the strut are determined by using the trial and error method according to the following formulae:

where superscript * represents the modified values, andk1andk2are the correction factors for the characteristic length of the pod and the strut, respectively. And the Reynolds number can then be modified via Eq.(19) by replacing the original geometric length of the pod and the strut with above characteristic lengths.

As shown in Fig.15, the correlation between the modified Reynolds number and the frictional drag coefficients of the bare pod body seems to be in fair agreement with the 1957 ITTC formula when the correction factorsk1andk2are taken as 1.2.Therefore,the correction factorsk1andk2will be adopted as the constant value of 1.2 in the following analysis.

Fig.15 Variation of the frictional drag coefficients of the pod and the strut with the Reynolds number with modified characteristic length for the bare pod body at different scales

(2)Determination of the characteristic velocity

The 25th ITTC report of the Propulsion Committee presented that the characteristic velocity of different components of the podded propulsor should be modified in the prediction of the pod resistance,and the correction factor could be related to the load of the propeller of the podded propulsor.Park (2014) and Tomi (2017)[8]also modified the characteristic velocity of the non-rotating components according to the propeller load during the analysis of the scale effect of the podded propeller.Fig.16 shows the dimensionless axial velocity (Vx/V) distribution around the puller podded propulsor at different scales,whereVxis the axial velocity andVis the inlet velocity.There are obvious differences between the inlet velocity (V) and the axial velocity after the propeller plane of the puller podded propulsor. It is suggested that appropriate characteristic velocities of non-rotating components can be related to the average relative flow velocity in front of the non-rotating components in order to consider the propeller induction effect. It is observed that the dimensionless axial velocity(Vx/V) distribution of the flow field around the pod and the strut is very similar for the podded propulsor under the same advance coefficient,but changes significantly with the advance coefficient.

Fig.16 Dimensionless axial velocity distribution around the puller podded propulsor

With a few attempts, for the geometry specified podded propulsor, the characteristic velocities of the non-rotating components are correlated to the inlet velocity through correction factors which are assumed to be power functions of the advance coefficient. The definitions of the characteristic velocities of the pod and the strut are written as follows:

whereα1andα2are the correction factors for the characteristic velocities of the pod and the strut,which are subsequently obtained by trial and error method based on the RANS results:α1=1.0777×J0.969;α2= 1.122 8×J0.960.

(3)Analysis with modified Reynolds number

The modified Reynolds number(Re*)can then be calculated as follows:

Fig.17 gives the variation of the characteristic velocity based frictional drag coefficients of the non-rotating components versus the modified Reynolds number at different working condition and scales. It shows that the correlation between the frictional drag coefficients and the modified Reynolds number is consistent with the 1957 ITTC formula without data dispersion as described in Fig.14.It is suggested that the modified Reynolds number can be applied to correct the scale effects of the frictional drag of the non-rotating components of the podded propulsor.

Fig.17 Variation of the frictional drag coefficients of the pod and the strut with modified Reynolds number for the puller podded propulsor at different scales

4.3 Proposal and verification of the current correction method

Based on the above research, a scale effect correction method for the open-water performance of the puller podded propulsor is proposed,and the specific steps (as shown in Fig.18)are briefly described as follows:

(1) Calculating the open-water characteristics (thrust coefficientKT, torque coefficientKQ) of a model-scale podded propulsor by CFD method(e.g.RANS method).

(2) Correcting theKTandKQof the propeller of the podded propeller from model scale to full scale by the 1978 ITTC formulae.

(3) Decomposing the drag of the nonrotating components into pressure drag and frictional drag, regard the pressure drag coefficient as constant for different scales, and calculate the frictional drag coefficient by using the 1957 ITTC formula. However, the Reynolds number should be modified according to Eq.(22).

(4)Adding different forces obtained from Step(2)and Step(3)to get the open-water characteristics of the full-scale podded propulsor. It should be stated again that the frictional drag of the non-rotating components at full scale shall be calculated by using the characteristic velocity (as calculated by Eq.(21))instead of the inlet velocity.

Fig.18 Flow chart of the proposed correction method

The proposed correction method focuses on the scale effect of the non-rotating components.Therefore, the drags of the non-rotating components of two large scales (the 1st:D=1.2,λ=6; the 2nd:D=2.4,λ=12 with 2.0×107≤Re≤2.2×107) are extrapolated from the model scale (D=0.2,λ=1)according to the proposed correction method, hereafter referred to asRe*correction method. The predicted results are then compared with the RANS results of the large scales for verification.Theβcoefficient method presented by the Krylov Ship Research Institute in Russia is also adopted for comparison and analysis. The ratio of the total drag of the non-rotating components at full scale to that at model scale,which is named asβcoefficient,is considered to be independent of advance coefficients. An averagedβcoefficient is used for the extrapolation from the model-scale puller podded propulsor (D=0.2,λ=1) to a larger-scale one (D=1.2,λ=6). Tab.7 presents the calculated RANS results (KD, Eq.(9)), the extrapolated results and their differences (Error), where Non,βandRe*correspond to the results without correction, the results corrected according to theβcoefficient method and theRe*correction method,respectively.

Tab.7 Comparison of drag coefficients between RANS results and extrapolated results

It can be found that the scale effect increases as the advance coefficient increases,with a maximum difference of 23.5%at the working condition with an advance coefficient ofJ=1.1.Both correction methods can reduce the errors between the extrapolated results and the RANS results under the majority of working conditions.The errors between the RANS results and the results that are extrapolated fromλ=1 toλ=12 by using theRe*correction method are within 9%for all the working conditions, while within 4% for working conditions with relatively greater advance coefficients. TheRe*correction method performs better than theβcoefficient method for working conditions with larger advance coefficients, confirming that theRe*correction method focusing on the correction of the scale effect of the frictional drag is more suitable when the frictional drag accounts for a relatively large amount of the total drag.

5 Conclusions

The current study of the scale effect of the open-water puller podded propulsor is carried out based on the RANS simulations. A method is then proposed for the correction of the scale effect on the open-water performance of puller podded propulsor according to modified Reynolds numbers(Re*)calculated by Eq.(22).The following conclusions can be drawn:

(1)The scale effect related to the pressure force of each component is small while the scale effect related to the frictional force of each component is relatively obvious.

(2) The overall scale effect of each component can be related to the proportion of frictional force in the total force. The scale effect of the non-rotating components is therefore larger than that of the propeller, and the scale effect under working conditions with larger advance coefficients is greater than that with lower advance coefficients.

(3) The proposedRe*correction method can reduce the errors of the extrapolated results under the majority of working conditions.While for the cases with larger advance coefficients,theRe*correction method performs better than theβcoefficient method.

(4) The correction factors that are involved in theRe*correction method, including the coefficients of characteristic length (k1andk2) and the coefficients of characteristic velocity (α1andα2),demand further discussion,such as the influence of the geometry,the propeller load,etc..The applicability and feasibility of the proposedRe*correction method requires further discussion for different types of podded propulsors.