梁中性轴的若干研究进展1)

张浩淼 任九生 张能辉

(上海大学力学与工程科学学院，上海 200444)

(上海市应用数学和力学研究所，上海 200444)

(上海市力学在能源工程中的应用重点实验室，上海 200444)

梁柱结构不仅是建筑工程和桥梁工程的主要结构形式，也是轮船、飞机机翼和起重机等机械结构中的重要承力构件。鉴于梁弯曲变形是杆件结构基本变形中最为复杂的变形形式，对梁弯曲变形的研究历史也最为曲折，对其中最为关键的中性轴位置的确定也经历了诸多学者的努力和不断探索。

梁的中性层是指弯曲变形时梁内纵向长度不变的一层，或者说弯曲变形时梁内既不伸长也不缩短的一层，而梁的中性轴指梁中性层与其横截面的交线。由单一机械载荷作用下梁的纯弯曲试验可知，弯曲后梁的纵线由直线变为弧线，靠近梁顶面或梁底面一侧的纵线伸长，而另一侧的纵线缩短，因此弯曲变形时梁内总有一层既不伸长也不缩短，即梁中性轴总是存在的[1-2]；在梁中性轴位置即坐标轴确定之后，便可由经典的单变量方法描述梁的弯曲正应变，即ε=y/ρ，其中y为考察点距离中性轴的坐标，ρ为中性轴处的曲率半径；而后便可进一步确定梁的弯曲正应力分布，即在梁的中性轴处弯曲正应力为零，在中性轴两侧，一侧正应力为正，而另一侧正应力为负，且正应力的大小与到中性轴的距离成正比。

1 梁中性轴的早期认识

最早在1620 年，比克门发现梁内存在中性轴，提出中性轴的概念。而后著名力学家如伽利略在1638年、胡克在1678 年、马略特在1686 年、伐里农在1702 年、伯努利在1705 年、库伦在1776 年等先后提出梁内存在中性轴，但伽利略、马略特、伐里农等均把中性轴取在梁的下侧，因此未能正确给出中性轴的位置[3-4]。帕伦在1713 年取得突破性的进展，指出梁中性轴在梁的中间某个位置，如矩形截面梁的中性轴在梁的上侧距离和梁高之比为9:11 的位置。直到1826 年，纳维在《力学在机械与结构方面的应用》一书中给出正确答案，即当材料服从胡克定律时，梁的中性轴通过截面形心。

对中性轴位置的正确回答要归功于胡克对梁中正应力分布的正确认识，1678 年胡克在《论弹簧》一书中指出梁中正应力是以中性轴处为零的线性分布，一侧受拉，而另一侧受压。然而，很难知道哪一层的正应力为零，那么只好借助梁截面轴向力平衡条件，即梁上弯曲轴力或净纵向力为零，或者说整个梁横截面上的正应力合力为零的条件，来确定中性轴位置。当材料服从胡克定律时，根据梁中正应力关于中性轴的分布方式可知，梁的中性轴必然通过截面形心。既然中性轴通过截面形心，当材料服从胡克定律时确定中性轴位置就比较容易了。对于具有对称结构的梁而言，对称轴就是中性轴；但对于具有非对称结构的梁，中性轴的确定需要计算组合截面的形心位置。

2 梁中性轴的当代进展

面对工程中新材料和新结构形式的大量使用，梁中性轴位置的确立又日益变得重要。当梁结构材料不服从单一的经典胡克定律时，梁中正应力关于中性轴的分布方式必然发生变化，导致梁的中性轴不再通过截面形心，中性轴位置一般仍然需由隔离体的轴向力平衡条件直接确定。而材料不服从单一胡克定律的情况也有诸多情形，有的是因为材料的非线性性质引起，如双模量梁、含损伤梁、弹塑性梁、功能梯度形状记忆合金梁等；有的是因为复杂加载条件或多物理场(热机耦合、热电耦合、磁电) 因素引起，如考虑热扩散影响的梁、考虑压电影响的梁等；有的是因为结构因素引起，如叠合梁和层合梁等。

对于非线性弹性梁，因其弹性模量是应变依赖的，即E(ε) =E0+E1ε，则由于几何中面轴向变形的约束使得横截面上产生轴向力，从而导致梁的中性轴位置发生变化，且中性轴位置随材料非线性程度Er=E0/E1而变化[5]。如图1 所示，对于两端固定的非线性弹性梁，其弯曲构形上的两个拐点把梁分成三部分，每一部分的中性轴位置都是连续变化的。图中变量解释详见参考文献，下同。

图1 非线性弹性梁的中性轴位置[5]

对于混凝土、铸铁、金属合金和橡胶等材料而言，其材料弹性系数在变形过程中是变化的，一般将受拉和受压阶段的弹性系数分别进行线性化处理，用双模量理论或不同模量理论表示。如图2(a)所示，对于双模量梁，中性轴总是偏向弹性模量高的一侧；特别地，对受压弹性模量大于受拉弹性模量的一般情况，中性轴总是偏向受压区[6-7]。

对于含损伤梁，因结构内部受损后必然导致截面材料刚度不均匀变化，随之中性轴位置发生变化。如图2(b) 所示，如果是单边损伤梁，其中性轴向未损伤的一侧移动，且损伤程度越大或载荷越大，中性轴偏离几何中面的距离越大；但如果是对称的多边损伤梁，其中性轴位置不变[8-9]。

对于弹塑性梁，当材料处于线弹性范围内时，中性轴必然是通过截面形心的；当材料屈服后，中性轴会发生偏移，且偏移与载荷、截面形状和材料模型均相关。如图2(c) 所示，材料进入塑性变形强化阶段后，一般压应力大于拉应力，从而造成拉压不平衡，即拉应力区和压应力区不再对称，且中性轴位置偏向受压区[10]。

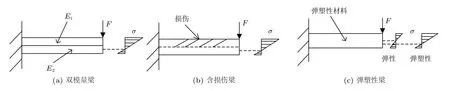
图2 不同材料梁中性轴的位置

对于由陶瓷和金属组成的金属在下侧的功能梯度材料梁，如图3 所示，在弹性变形阶段，由于陶瓷材料弹性模量和屈服应变低，中性轴向陶瓷侧偏移，偏移值不随外加弯矩变化而变化；在弹塑性变形阶段，中性轴向受拉侧逐渐偏移，且偏移值随外加弯矩的增加而增大；在完全塑性变形阶段，中性轴先向受拉侧偏移，且偏移值随外加弯矩的增加而增大，但偏移达到一个最大值后，偏移值却随外加弯矩的增加而减小，即向受压侧回移；在卸载阶段，中性轴偏移量随外加弯矩的减小单调变小，卸载结束后最终的偏移值取决于卸载初始时刻的弯矩值。总的来说，中性轴总是位于截面形心以上，即偏向陶瓷一侧[11]。

图3 功能梯度材料梁的中性轴位置[11]

对于考虑热扩散影响的梁，因温度的升高或降低会在梁中产生轴向拉力或轴向压力，如图4 所示，考虑轴向压力作用时，在轴向压力作用下中性轴会向截面拉伸区偏移，且偏移大小与轴向压力大小或温度变化值有关[12]。

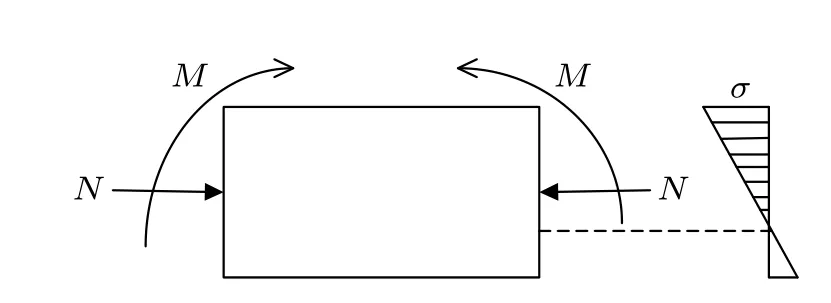
图4 有轴向压力作用时梁的中性轴位置

对于形状记忆合金梁，因形状记忆合金的马氏体相变导致梁弹性模量减小，会造成拉压不平衡，也就是拉压应力区不对称，中性轴位置会发生偏移，且偏移情况随材料相变不同发展阶段而变化。如图5所示，当梁受拉侧表层首先发生相变时，中性轴会向受压侧偏移；在仅有受拉侧发生相变的一阶相变阶段，中性轴向受压侧的偏移逐渐增大；在受压侧和受拉侧同时发生相变的二阶相变阶段，梁弹性模量减小到最小值，中性轴向受压侧偏移量达到最大；在仅有受拉侧完全转化为马氏体相的三阶相变阶段，梁弹性模量逐渐增大，中性轴向受拉侧的偏移逐渐回移；在受压侧和受拉侧同时完全转化为马氏体相的四阶相变阶段，中性轴逐渐回移到初始位置[13]。

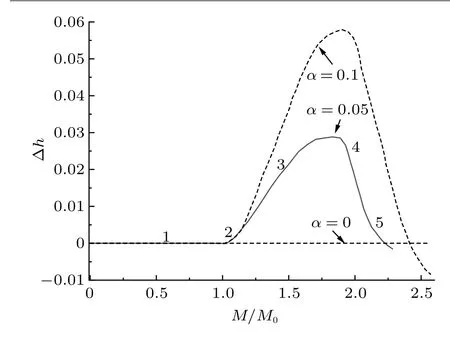
图5 形状记忆合金梁的中性轴位置[13]

土木工程中通常采用叠合、焊接和粘接等加固法形成叠合梁和层合梁对原有结构进行加固处理，若两梁接触面光滑则称为叠合梁，若两梁加固成整体且无相对滑动则称为层合梁。如图6 所示，对于叠合梁而言，每根小梁有各自的中性轴，均通过各自的形心，且正应力按各自的中性轴正比分布[14]；当叠合梁中两梁接触面有摩擦时，上下梁的中性轴都由相应的形心向接触面偏移，即上梁中性轴位于其形心下方，下梁中性轴位于其形心上方[15]。对层合梁可由直接分析法，根据脱离体轴向力平衡条件或等效截面法(相当截面法) 求得中性轴位置，其位置一般与各层面积和材料弹性模量有关。对两类不同材料层合梁而言，中性轴会偏离几何中心而向高弹性模量区移动[16-17]。

图6 双层梁的中性轴位置

值得一提的是，在解决多物理场作用下新材料、新结构的力学问题时，大多数研究采用单变量方法描述结构的应变场，但单变量方法限制坐标系建立在中性轴上，所以中性轴的确定成为问题的关键，或者说，中性轴的位置成为力学模型中一个隐含的变量，可见需要发展更为简洁的描述方法。

3 微纳层合梁的中性轴问题

近年来，利用微纳制造技术和现代传感技术等制备的微梁层合结构，因其具有无需标记、快速、实时、高灵敏度和方便携带等优点，在医学检测、环境监测、医药开发和军事安全等领域有广泛的应用，吸引了众多学者的关注。正如前面所述，对于梁理论而言，如何描述梁的应变场是关键所在。在经典宏观梁的单变量理论中，应变场的度量或其坐标系的基准是中性轴，所以利用经典方法时必须先确立梁中性轴的位置。但对于微纳梁而言，由于具有较大的表体比，需要计入通常简化为切向作用的表面应力效应，或需要引入表征非局部效应的非经典连续介质本构关系[18-19]，加之需要考虑器件服役时多物理场的耦合作用，这些新的效应给微纳梁结构中性轴的定位问题带来了挑战。

关于层合梁问题，针对热适配问题，早在1925年，Timoshenko[20]提出了先在各层寻找中性轴再利用层间连续条件的叠加法，但当结构层数过多时，方程求解变得较为繁琐；针对压电层合结构问题，Weinberg[21]放弃了将坐标系建立在中性轴上的经典思维范式，提出了以中性轴位置作为新变量显示化在应变场描述中的两变量方法；Hsueh[22]将原来一个轴向力为零的平衡方程拆解为均匀应变和弯曲应变引起的轴力分别为零的两个方程，提出了寻找弯曲轴的Hsueh 三变量法；针对功能梯度材料梁问题，Zhang 等[23]提出了与寻找弯曲轴方法类似的物理中面法；Zhang 等[24-25]基于两个参考面提出了更为简洁的张氏两变量法，即ε=ε0-y/ρ，其中ε0为坐标轴处的正应变，ρ仍为中性轴处的曲率半径；该方法既不同于将坐标系建在中性轴上的经典单变量方法[1-2]，也不同于Freund 提出的基于一个参考面描述应变场的两变量假设法[26]。目前张氏两变量新方法已广泛用于核冷却系统、光伏电池、钻井套管、电阻式存贮器、铺设路面和热障涂层等设计研究中[27-32]。

值得注意的是，当分子或原子吸附在微梁的上下表面会形成表面应力差，这个吸附表面应力会引起微梁的弯拉或弯压组合变形，变形后微梁的中性轴位置会发生变化，如图7 所示，在微梁上表面受拉吸附应力作用下，吸附稳定后微梁的中性轴位置将下移，下移量取决于微梁功能层和基底层的厚度和弹性模量[33]。对于均匀温度场和机械载荷作用下的层合微梁，如图8 所示，随着加载参数比λ的变化，零应变轴是唯一的，但零应力轴可能不唯一，换句话，零应力轴的个数和位置取决于弹性模量、基底和膜的厚度比、力学和温度加载条件[34-35]，这势必给基于零应力确立中性轴(即零应变轴)位置的传统单变量方法带来挑战，而借助上述Hsueh 三变量法[22]和张氏两变量法[24-25]等可巧妙地规避这一难题。

图7 表面应力作用下微梁的中性轴位置[33]

图8 在外部力矩和内部热应力作用下双层微梁不同轴线的比较[36]

4 结语

梁中性轴位置的确定是预测梁结构变形和应力分布的基础，也是进而解决梁强度、刚度、稳定性问题的关键。首先，诸多前辈基于中性轴概念，历经一百多年的探索，给出了描述应变场的单变量方法，获得了纯弯曲均质梁中性轴必然通过其截面形心的基本结论。后来随着新材料和新结构的不断涌现，如双模量梁、含损伤梁、弹塑性梁、层合梁、组合梁、考虑热效应的梁、压电梁、功能梯度梁和形状记忆合金梁等，使得中心轴的漂移成为必须解决的棘手问题。而近二十年微纳梁结构中的表界面效应、非局部效应和多物理场耦合效应进一步推动发展了更为精确和简便的Hsueh 三变量方法、物理中面法、张氏两变量方法等。对于梁中性轴问题的历史回顾和正确认识对于合理有效地解决建筑、桥梁、机械结构、微电子器件等相关问题有重要的现实意义。