装配式矩形水池杯口节点的刚度研究

王泽明 王长祥 徐辉 张松 荣彬

1.中国市政工程华北设计院研究总院有限公司 天津300381

2.天津大学建筑工程学院 300072

引言

装配式水池预制化程度高，安装简单方便，可以大量减少现场的湿作业，因此具有施工周期短、快速投入使用等优点，符合绿色低碳的发展理念。目前杯口节点在装配式矩形水池中已经逐渐得到应用［1-3］。但在现有设计标准中，尚缺少对于装配式矩形水池杯口节点计算模型的相关规定。《给排水工程预应力混凝土圆形水池结构技术规程》（CECS 216：2006）［4］规定了环形杯口节点按照铰接节点模型进行设计，《给水排水工程钢筋混凝土水池结构设计规程》（CECS 138：2002）［5］规定了现浇矩形水池底板和池壁节点按照刚接节点模型进行设计，对于装配式矩形水池杯口节点的设计模型，两者均未给出相关规定。

对于节点类型的划分，欧洲规范［6］根据试件初始转动刚度的大小将节点划分为刚性节点、半刚性节点和柔性节点，美国规范［7］根据试件弯矩-转角曲线割线与梁线刚度比值区分节点类型。Bjorhovde［8］考虑节点初始刚度和极限抗弯承载力提出一种线性节点分类方法，将节点分为铰接、半刚性连接和刚接，该种分类方法简单方便，但容易对节点类型进行错误的划分。Hasan［9］提出非线性节点划分方法，根据绝对刚度大小对节点进行分类。

针对预制混凝土节点类别的划分，赵斌［10］通过在梁单元端部装带有转动弹簧的力学模型，根据预制混凝土节点转动刚度和梁线刚度的比值对预制混凝土节点进行分类。刘颖［11］等人通过理论分析和数学推导，提出按照梁的线刚度和节点转动刚度的比值作为节点分类标准。鲁浩［12］将半刚性单元作为结构力学基本单元，推导不同荷载作用下结构的内力，引入节点相对转动刚度和和相对刚度比，根据相对刚度比对预制混凝土节点进行分类。

为研究装配式矩形水池杯口节点的刚度，本文建立有限元模型进行低周反复荷载试验模拟，并与已有抗震性能试验［13］数据对比，验证有限元分析的准确性。在此基础上，对装配式矩形水池杯口节点进行参数化分析，考察节点破坏形态、滞回曲线、弯矩-转角曲线等模拟结果，并对装配式矩形水池杯口节点的抗震性能和节点类型进行研究。

1 有限元模拟准确性的验证

1.1 有限元模型

利用ABAQUS有限元分析软件分别建立文献［13］中的现浇钢筋混凝土节点、平口式套筒灌浆节点及插承式套筒灌浆节点有限元模型。文献［13］为研究节点在低周往复荷载作用下节点的力学性能，因此本文采用混凝土塑性损伤模型。塑性参数膨胀角和偏心率分别为30 和0.1，K和屈服强度应力比分别取0.667 和1.16，黏滞系数为0.0005。混凝土采用《混凝土结构设计规范》（GB-50010—2010）规定的本构关系。

钢筋本构关系模型采用清华大学潘鹏等［14］在ABAQUS 基础上开发的一组PQ-Fbier 中的USTEEL02 钢筋本构关系的集合，USTEEL02 本构关系模型是一种随动硬化单轴本构关系模型，其加载刚度与Clough本构关系有关，如图1 所示。

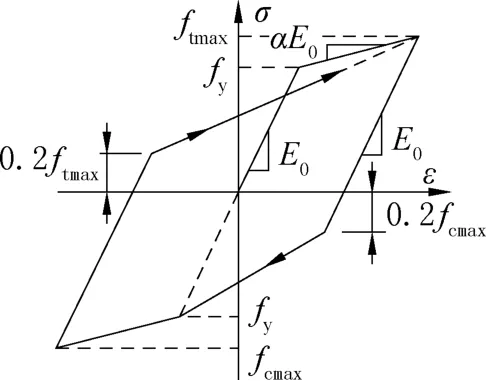
图1 钢筋反向加载本构关系Fig.1 Constitutive relation of steel bar under reverse loading

建立的有限元模型如图2 所示。混凝土单元类型为C3D8R 三维实体单元，钢筋单元类型为T3D2 桁架单元，钢筋与混凝土之间添加非线性弹簧进行约束。混凝土和钢筋的属性与几何尺寸均同试验保持一致。模型约束为：约束底板下表面的位移和转角实现固定，壁板上端自由，如图2a 所示。其中预制壁板与底板之间采用弹簧模型的法向切向本构关系［15］，如图2b所示。分析时在模型上端部施加水平低周反复荷载，加载制度与试验保持一致。本文中需要得到滞回曲线，设置输出历史变量分别为空间位移U及反力RF等。

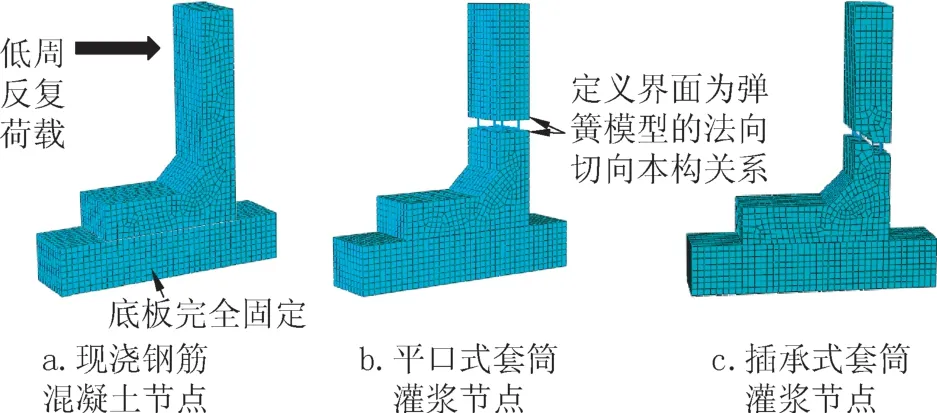
图2 有限元模型Fig.2 Finite element model

1.2 结果对比分析

骨架曲线为结构在循环荷载作用下，每级荷载第一个循环周期峰值荷载的连线，反应了结构的延性、刚度等重要特征。图3 给出了有限元模拟与试验结果的荷载-位移骨架曲线。由图可知，有限元模拟的骨架曲线与试验结果完全吻合。在加载初始阶段，有限元模拟与试验的荷载-位移均呈线性关系。随着荷载的增加，混凝土损伤加剧，表现为骨架曲线变缓，斜率逐渐减小。当达到峰值荷载时，位移急剧增加，荷载缓慢下降，三个试件均表现出较好的承载能力。

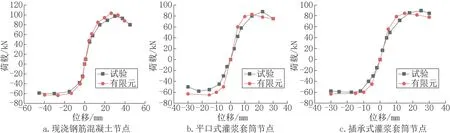
图3 骨架曲线Fig.3 Skeleton curve

有限元模拟的现浇钢筋混凝土节点峰值荷载均大于平口式套筒灌浆节点和插承式套筒灌浆节点峰值荷载，且平口式套筒灌浆节点和插承式套筒灌浆节点骨架曲线几乎相同，结果表明这两种连接节点差异较小。上述结论与试验结果完全一致。

通过有限元模拟与已有试验对比，结果表明有限元模拟与试验完全吻合，有限元模拟的准确性得以验证。

2 装配式矩形水池杯口节点有限元模拟

2.1 杯口节点参数

基于上述验证的有限元分析，对装配式矩形水池杯口节点刚度进行研究。杯口节点截面如图4 所示，其中杯槽高度（h）与杯槽外伸长度（w）为变量，其余参数为定值，壁板厚度取为200mm，高度为4000mm。壁板与杯槽之间采用C45 细石混凝土填充，壁板及杯槽均采用C40 混凝土。模型按照构造要求配筋，且均不考虑防水措施。表1 给出了杯口节点有限元模型参数信息，模型编号为SJ-w-h，如SJ-200-200表示为模型杯槽外伸长度为200mm，杯槽高度为200mm。

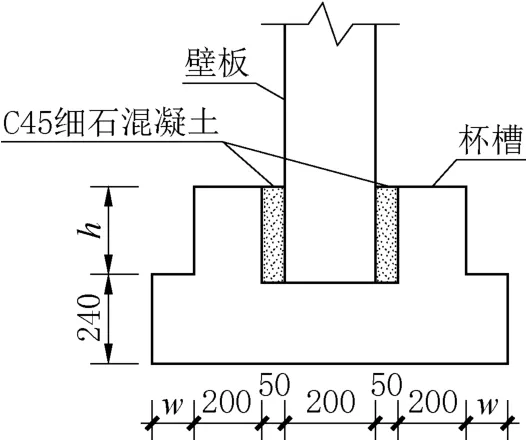
图4 杯口节点截面（单位： mm）Fig.4 Section of socket joint（unit：mm）

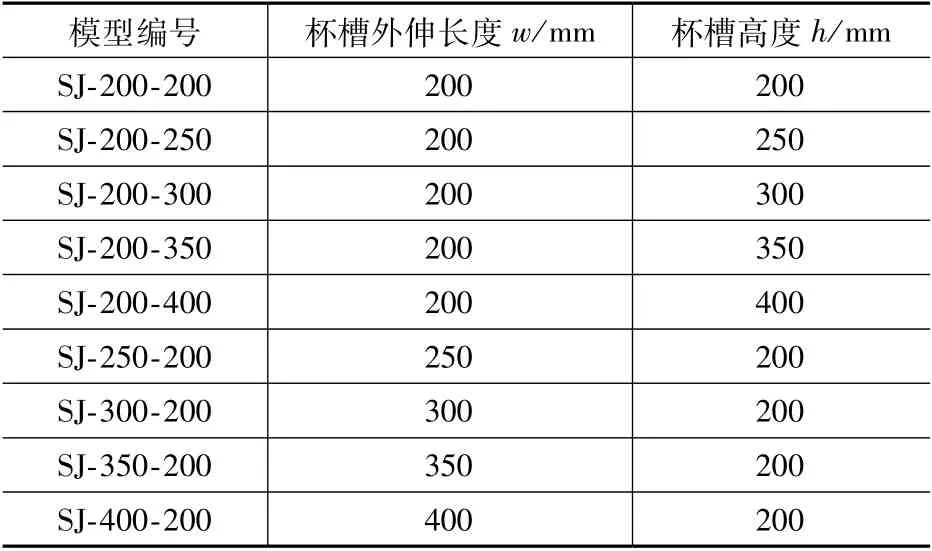
表1 杯口节点有限元模型参数Tab.1 Information of socket joint finite element model

2.2 杯口节点有限元模型

为提高有限元分析速度，模型纵向长度取为500mm，杯口节点典型有限元模型SJ-200-200 如图5 所示。壁板、细石混凝土及底板之间采用弹簧模型的切向法向本构关系，模型其余信息参考2.1 节中有限元模型信息。模型约束为：杯槽下表面约束位移及转角，壁板上端自由。在壁板顶端施加水平低周反复荷载。加载制度如图6 所示，加载以10mm位移为增量，每级荷载往复循环两次。通过有限元模拟，发现按照上述加载制度进行加载时，当位移增加至70mm时，水平荷载大约下降至最大水平荷载的85%。

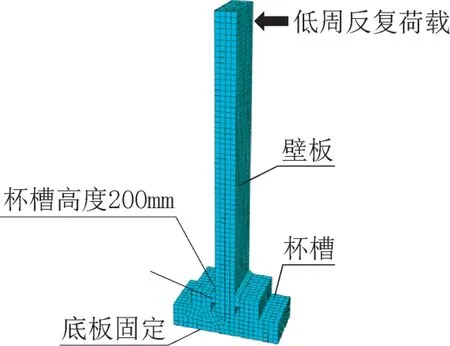
图5 SJ-200-200 有限元模型Fig.5 Finite element model of SJ-200-200

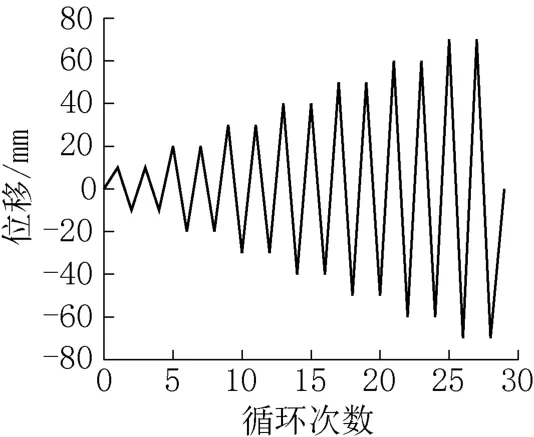
图6 低周反复荷载加载制度Fig.6 Low reversed cyclic loading system

2.3 有限元结果分析

1.典型结果分析

图7a为典型模型的钢筋应力图，由图可知：壁板竖向受力钢筋应力在杯口上端部最大，而在杯口内部应力较小。该现象表明壁板在杯口内部位移及转角较小，钢筋基本未发生较大变形，而在杯口上端部壁板承受弯矩最大，变形较大，钢筋应力最大。混凝土应力见图7b，在循环荷载作用下，杯口上端部混凝土拉应力最大。通过分析钢筋及混凝土应力，结果表明底板与壁板以杯口形式连接的节点具有良好的受力性能，而杯口节点上端部为杯口节点薄弱部位，混凝土容易产生裂缝。

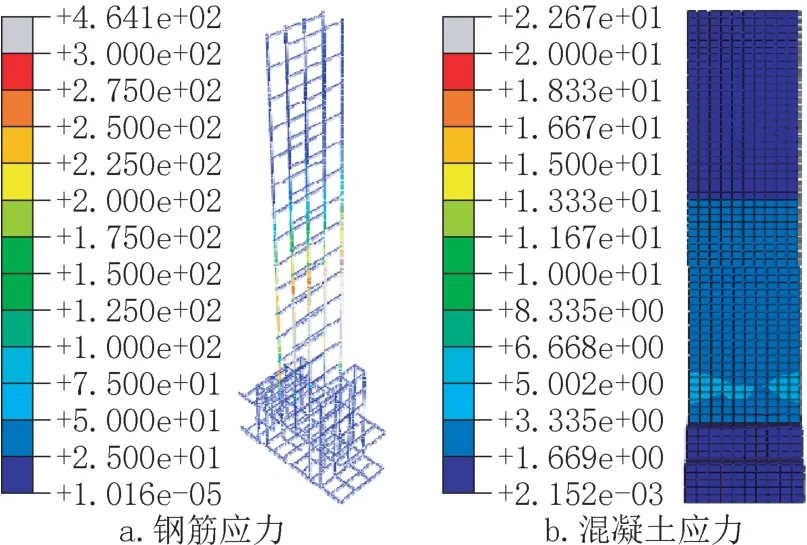
图7 SJ-200-200 钢筋及混凝土应力（单位： MPa）Fig.7 Steel stress and concrete stress of SJ-200-200（unit：MPa）

在低周反复荷载作用下，得到结构的滞回曲线。其反映结构在反复受力过程中的变形特征、刚度退化及能量消耗，是确定恢复力模型和进行非线性地震反应分析的依据。图8 给出典型有限元模型滞回曲线，可以看出，滞回曲线为梭形，滞回曲线形状饱满，表明模型的塑性变形能力较强，具有很好的抗震性能和耗能能力。

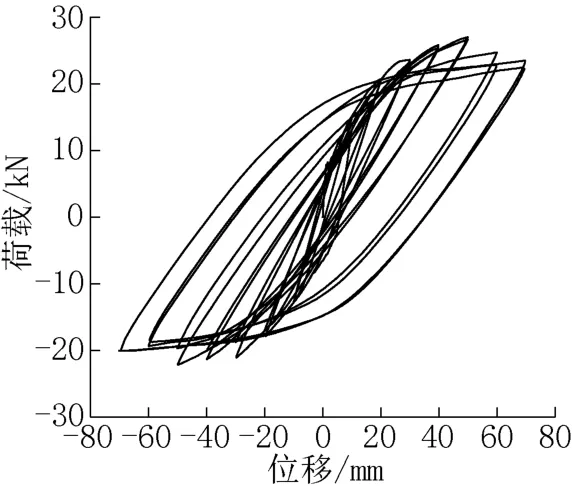
图8 SJ-200-200 滞回曲线Fig.8 Hysteretic curve of SJ-200-200

2.杯槽高度分析

图9 为5 个有限元模型的荷载-位移骨架曲线，通过骨架曲线可知，模型均经历从弹性阶段达到峰值荷载再到承载力下降的过程。在弹性阶段，骨架曲线近似为一条直线，荷载值与位移为线性关系。随着荷载的增加，骨架曲线斜率变小，荷载与位移不再遵循线性关系，说明混凝土产生损伤，钢筋逐渐屈服。当达到峰值荷载时，位移急剧增加，荷载下降，表明模型已经发生破坏。同时由图可以看出，提高杯槽的高度，能够提高模型极限承载力。

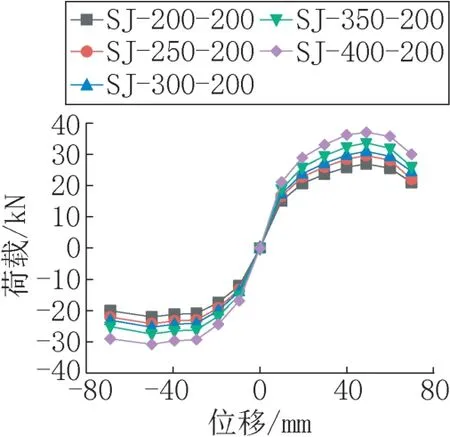
图9 荷载-位移骨架曲线Fig.9 Load-displacement skeleton curve

图10 给出了有限元模型的弯矩-转角曲线，可以看出，5 个模型的弯矩-转角曲线变化趋势与荷载-位移骨架曲线变化趋势一致，但是随着杯槽高度的增加，模型的最大转角逐渐减小。由弯矩-转角曲线得到不同杯槽高度下各模型的特征点情况如表2 所示。

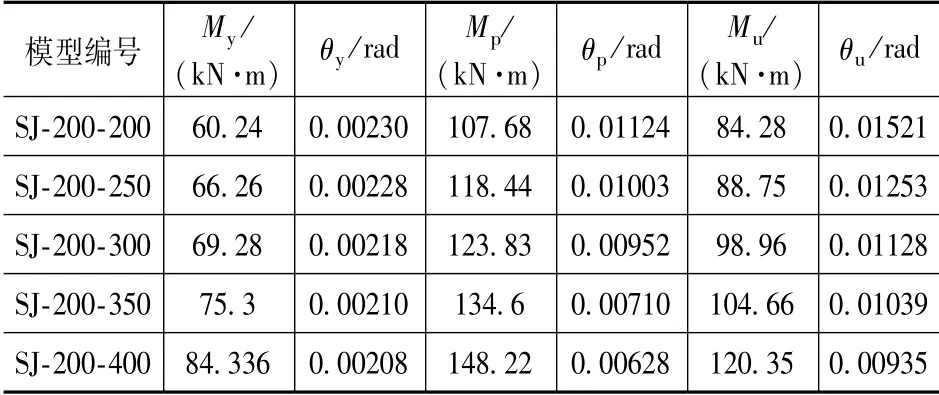
表2 弯矩-转角曲线特征点情况Tab.2 Characteristic point information of moment-rotation curve

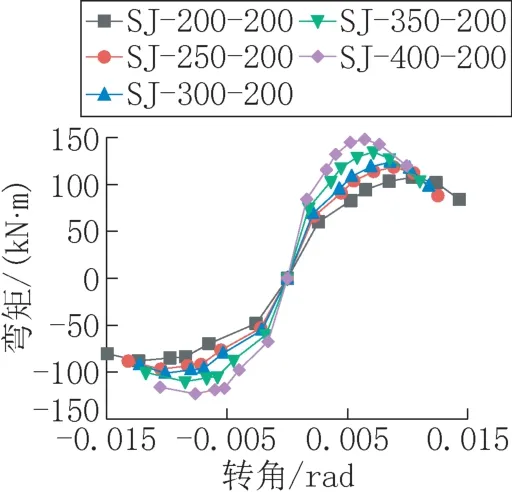
图10 弯矩-转角曲线Fig.10 Moment-rotation curve

模型极限承载力和初始转动刚度与杯槽高度之间的关系如图11 所示，由图可知，增加杯槽高度，能够提高杯口节点的极限承载力与初始转动刚度。杯槽高度每提高50mm，杯口节点极限承载力与初始转动刚度分别提高了约7.32%及9.22%。该结果表明，杯槽高度的增加，改善了杯口节点的受力性能。

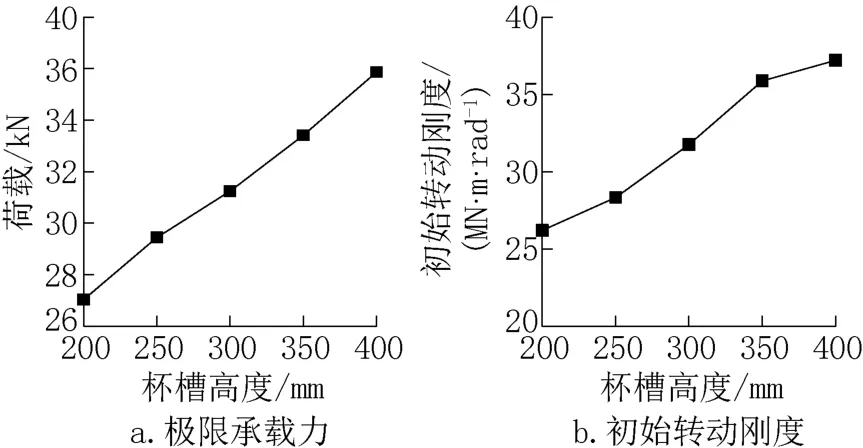
图11 极限承载力和初始转动刚度与杯槽高度的关系Fig.11 The relationship between ultimate bearing capacity or initial rotational stiffness and the height of groove

3.杯槽外伸长度分析

图12 为5 个有限元模型的骨架曲线，通过骨架曲线可知，模型同样均经历从弹性阶段达到峰值荷载再到承载力下降过程。在弹性阶段，骨架曲线近似为一条直线，荷载值与位移为线性关系。随着荷载的增加，骨架曲线斜率变小，荷载与位移不再遵循线性关系，说明混凝土产生损伤，钢筋逐渐屈服。当达到峰值荷载时，位移急剧增加，荷载下降，表明模型已经发生破坏。同时由图可以看出，各模型的骨架曲线近似重合，结果表明当杯槽外伸长度大于壁板厚度时，增加杯槽外伸长度不能提高杯口节点的力学性能。

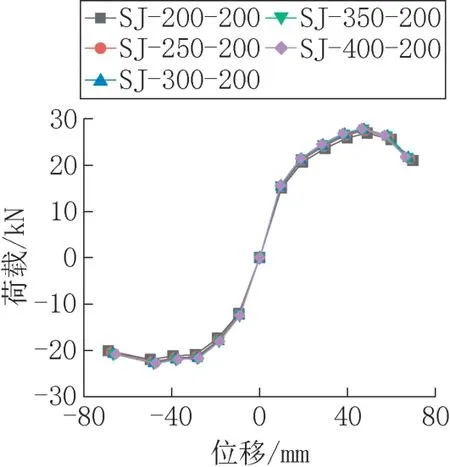
图12 荷载-位移骨架曲线Fig.12 Load-displacement skeleton curve

图13 给出了有限元模型的弯矩-转角曲线，可以看出，5 个模型弯矩-转角曲线变化趋势与荷载-位移骨架曲线变化趋势一致。由弯矩-转角曲线得到不同杯槽外伸宽度下各模型的特征点情况如表3 所示。

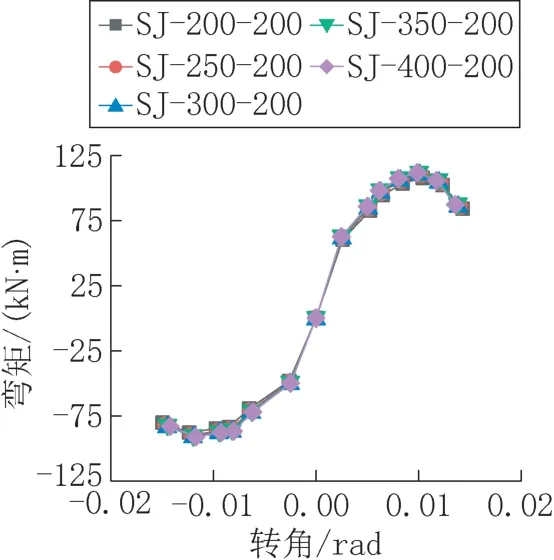
图13 弯矩-转角曲线Fig.13 Moment-rotation curve

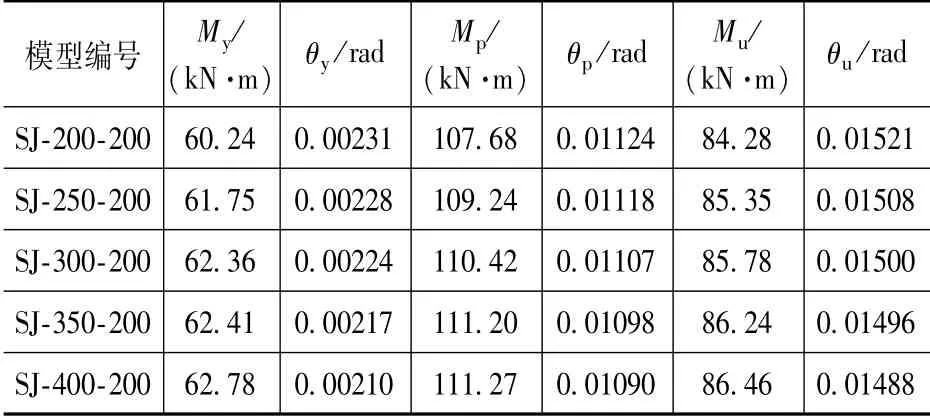
表3 弯矩-转角曲线特征点情况Tab.3 Characteristic point information of moment-rotation curve

模型极限承载力和初始转动刚度与杯槽外伸长度之间的关系如图14 所示，由图可知，杯槽外伸长度每增加50mm，杯口节点极限承载力与初始转动刚度分别提高了约0.91%及3.3%。该结果表明，杯槽外伸长度的增加，几乎不能提高杯口节点的极限承载力，对杯口节点初始转动刚度影响有限。

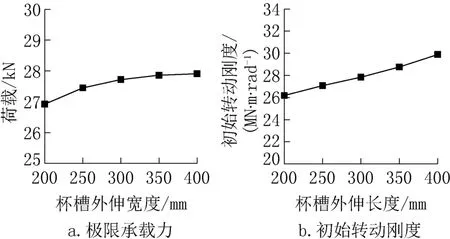
图14 极限承载力和初始转动刚度与杯槽外伸长度的关系Fig.14 The relationship between ultimate bearing capacity or initial rotational stiffness and the protruding length of groove

4.装配式矩形水池杯口节点类型判断

由弯矩-转角曲线得9 个杯口节点模型的初始转动刚度及壁板线刚度见表4。根据文献［10］及文献［11］对预制混凝土节点类型划分标准对9个杯口节点模型进行划分，如图15 所示。由图15a可以看出，根据文献［10］的划分标准，模型SJ-200-350 及模型SJ-200-400 初始转动刚度属于刚接区间，其余模型初始转动刚度均属于半刚接区间。由图15b 可知，根据文献［11］的划分标准，所有模型初始转动刚度均属于半刚接区间。

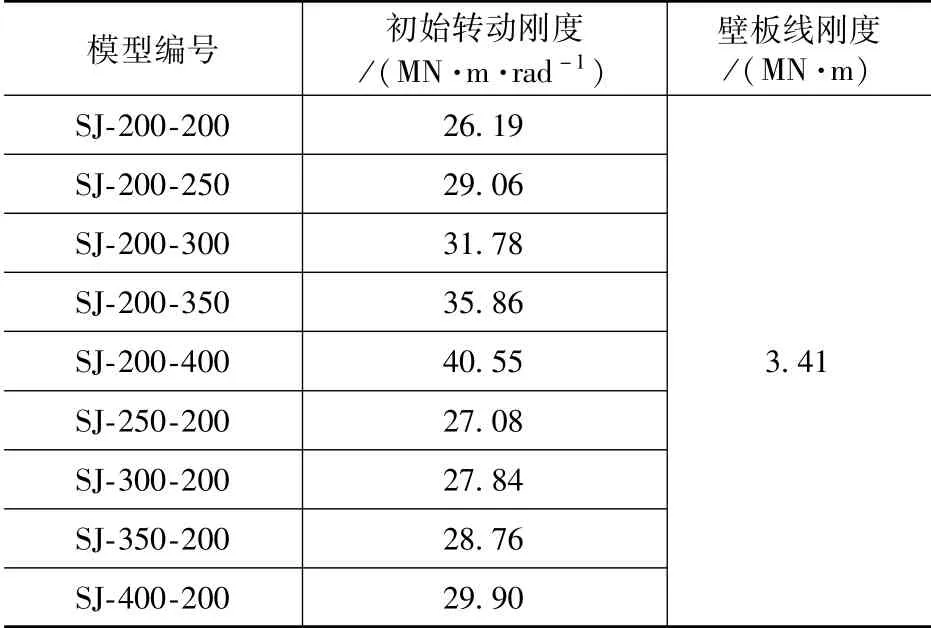
表4 杯口节点刚度Tab.4 Stiffness of socket joint

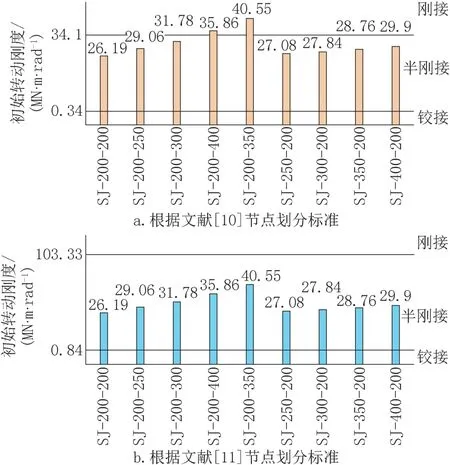
图15 杯口节点类型划分Fig.15 Classification of socket joint

由上述分析可知，根据文献［10］及文献［11］的划分标准对装配式矩形水池杯口节点类型的划分存在差异，但大部分杯口节点的初始转动刚度均属于半刚接区间。虽然模型SJ-200-350 及模型SJ-200-400 按照文献［10］的划分标准属于刚接，但初始转动刚度也靠近半刚接区间。

综上所述，装配式矩形水池杯口节点应作为半刚接节点。

3 结论

本文通过有限元模拟与已有试验进行对照分析，验证了有限元模拟的准确性。在此基础上，对装配式矩形水池杯口节点刚度进行有限元分析研究。研究结果表明：

1.装配式矩形水池杯口节点应作为半刚性节点，其中滞回曲线饱满，表明该节点的变形能力较强，具有较好的抗震性能和耗能能力。

2.杯槽高度每提高50mm，杯口节点极限承载力与初始转动刚度分别提高约7.32%及9.22%。杯槽高度的增加，有利于提高杯口节点的力学性能。

3.杯槽外伸长度的增加，几乎不能提高杯口节点的极限承载力，对杯口节点初始转动刚度影响有限。

4.在水平荷载作用下，在杯口节点内部壁板与底板变形协调且钢筋应力较小，而在杯口节点上端部壁板受力钢筋和混凝土拉应力最大，该处混凝土容易产生裂缝，应做好防渗漏处理。