钢-聚乙烯混杂纤维水泥基复合材料与钢筋粘结锚固性能有限元分析

2021-12-31魏巍刘诗恒毛维浩

特种结构 2021年6期

魏巍刘诗恒毛维浩

1.重庆大学土木工程学院 400045

2.山地城镇建设与新技术教育部重点实验室（重庆大学） 400045

引言

工程水泥基复合材料（ECC）最先由Li［1，2］教授基于微观力学和断裂力学原理提出。该材料表现出优异的应变硬化性能和抗裂缝能力，故国内外研究人员试图利用该材料替代传统的普通混凝土，以改进和提升钢筋与混凝土的粘结性能。章文纲［3］进行了钢纤维混凝土的低周反复拉拔试验，结果表明，钢纤维混凝土与钢筋的粘结强度和刚度相比普通混凝土有较大提高。Lee 等人［4］通过钢筋拔出试验证实，聚乙烯醇纤维混凝土试件（PVA-ECC）中的钢筋锚固长度比普通混凝土中的小14%，并提出了钢筋在PVA-ECC中的粘结-滑移模型。Huang［5］等人进行了钢-聚丙烯混杂纤维混凝土试件（PP-ECC）的拔出试验，结果表明，混杂纤维的引入对粘结强度有明显的提升，并提出了考虑纤维增强、箍筋约束和变形钢筋几何形状影响的极限粘结强度分析模型。

目前通过掺加钢纤维和聚乙烯纤维，已配制出钢-聚乙烯混杂纤维水泥基复合材料，试验表现出拉伸应变硬化特性，其拉伸应变能力可达到4%，极限拉伸强度接近7MPa，且受压弹性模量达到28GPa，是普通混凝土理想的替换材料。基于此，本文以试验数据为依据，通过建立有限元模型来模拟变形钢筋与新型混凝土之间的粘结性能。

1 有限元分析与建模

本文利用大型通用有限元分析软件ABAQUS进行有限元建模分析，具体建模过程如下述。

1.1 变形钢筋钢肋的模型建立

以直径14mm的国产月牙形钢筋为例，正视图如图1a 所示，各横肋之间的倾角和间距分别标记为θ和L，肋的投影图如图1b所示，钢筋的尺寸参数H0、D、K、H见图1。

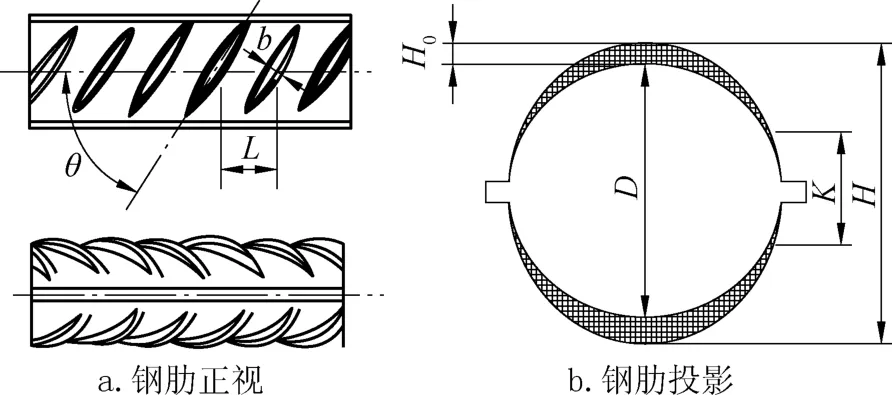
图1 钢肋Fig.1 Steel ribs

由国家标准《钢筋混凝土用钢第2 部分：热轧带肋钢筋》（GB／T 1499.2—2018）［6］，参考刘明等人［7］文中的表1，本文图1b中阴影部分面积即钢筋的相对肋面积FR、肋高H0、钢筋内径D、横肋间距L、横肋末端间隙K、钢筋外径H按表1 取值。

表1 钢筋外形特征值Tab.1 Characteristic value of steel rebars shape

基于Cai 等人［8］提出的高精度有限元模型，考虑将钢筋的月牙肋简化为多个平行的同心圆环，如图2 所示。其中B和H′0为简化后的钢肋高度和宽度，计算方法见Cai 等人运用的几何面积法。

图2 同心圆环Fig.2 Concentric ring

1.2 钢筋的单元类型和本构模型

钢筋采用ABAQUS单元库中的八节点六面体线性减缩单元即C3D8R实体单元。

钢筋的本构模型采用理想弹塑性模型，数字表达式见式（1）、（2）。钢筋的弹性模量Es取为2.08 ×105MPa，泊松比取为0.20。

1.3 ECC混凝土的单元类型和本构模型

ECC混凝土采用C3D8R实体单元进行建模。

损伤塑性模型适用于单调、循环和动态加载作用下损伤、裂缝变化的情况，故采用ABAQUS中的混凝土损伤塑性模型［9］模拟混凝土的力学行为。采用欧洲规范2［10］建议的本构关系，在该规范的基础上，根据《ABAQUS 混凝土损伤塑性模型参数验证》［11］的规定，在ABAQUS中将拉伸恢复系数取为0.35。

1.4 ECC混凝土与钢筋的组合

对于混凝土与钢筋的接触面，法向定义为“硬接触”，切向定义为罚函数摩擦模型，摩擦系数取为0.45。

1.5 模型建立与网格划分

将各PART部分组装成拉拔试块，得到本算例建立的有限元分析模型。其中，ECC混凝土尺寸为150mm ×150mm ×100mm，钢筋长400mm，锚固长度为3 倍钢筋直径，即42mm。

网格种子密度和网格的大小对计算效率和计算准确性的影响较大，布种的密度不宜过大或过小，且xyz三个方向上的种子密度宜保持较小的差距。

单元划分采用扫掠网格划分。有限元模型及网格划分如图3 所示。

图3 有限元模型及网格划分Fig.3 Finite element model and meshing

1.6 边界条件

边界条件、加载方式可以在初始分析步中定义。对垂直于钢筋纵向（即xy面）、靠近加载端的混凝土面进行xy面上的完全固定约束（U1 ＝U2 ＝U3 ＝UR1 ＝UR2 ＝UR3 ＝0，其中：U代表位移，UR代表转角）。在钢筋加载端截面圆心建立参考点RP-1，再将参考点与钢筋加载端侧表面耦合。本算例采用位移加载，在该耦合点施加沿z方向的位移10mm。

2 有限元模拟结果比较

实际上，粘结应力在粘结长度范围内的分布并不是均匀的，而是一个变化的数值，但由于本次中心拉拔试验中钢筋的粘结长度较短，为了便于计算，一般认为其与基体之间的粘结应力在粘结长度范围内是均匀分布的。可采用平均粘结应力来反映钢筋与基体之间的粘结强度，公式如下：

式中：τ为平均粘结应力（MPa）；F为试验荷载（kN）；d为钢筋直径（mm）；la为钢筋粘结长度。

ABAQUS计算完毕后粘结锚固区段的应力云图如图4 所示。输出ABAQUS 计算完毕后的荷载-位移曲线，依据公式（3）进一步处理为粘结应力-滑移关系曲线并利用Origin 专业绘图软件绘制出相应曲线。将试验结果与本次ABAQUS模拟值进行对比，如图5 所示。

图4 粘结锚固区段应力云图（单位： MPa）Fig.4 Stress nephogram of bond anchorage zone（unit：MPa）

由图5 可见，有限元模拟所得的粘结应力-滑移关系曲线与试验值吻合良好，模拟曲线中峰值粘结应力为24.137MPa，与试验峰值粘结应力25.289MPa的误差在5%以内；当平均滑移量达到6mm后，曲线趋于平缓，说明ECC 试件表现出了明显的延展性；曲线下降段走势相似，模拟较为精准，说明本文的有限元分析模型及方法可以较准确地反映钢-聚乙烯混杂纤维水泥基复合材料与变形钢筋的粘结滑移关系。