科研数据分析软件在《大学物理实验》课程中的应用
——以电介质介电常数测量实验为例
2021-12-30任银娟何学敏李三龙李永涛
任银娟,何学敏,李三龙,李永涛
(南京邮电大学 理学院,江苏 南京 210023)
《大学物理实验》是一门将物理理论与实验操作充分结合的课程,也是全国高校理工科专业学生的必修基础课。该课程要求学生在理解实验原理的基础上,独立操作实验仪器、记录实验数据、分析处理实验数据并完成实验报告的撰写。这一过程与物理学家们发现许多重要物理现象的过程相似。其中,实验数据的分析与处理是非常重要的一个环节,它决定了得出怎样的实验结论,进而影响了对物理本质的理解。
实验数据处理的基本要求是客观、准确和有效。随着信息技术的发展,利用数据分析软件来处理实验数据,不仅规避了人工作图和计算时的主观性强、精度不高、准确度不够等问题,而且极大提高了数据处理的时间效率。此外,也正是得益于信息技术的发展,现在的本科学生基本上都具有一定的计算机技术基础,而且,高等院校普遍开设了关于计算机的通识课,这些课程有助于学生利用软件来处理实验数据。更为重要的是,理工科学生们在后续的本科毕业设计或者以后的硕士、博士学习期间很多都会用到科研数据分析软件,因此,将这些软件应用到大学物理实验课的教学中也将为学生们以后的学习研究打下基础。在众多科研数据分析软件中,Origin凭借其功能强大、易于学习掌握的特点被广泛应用,而且实践表明[1-5],利用Origin进行数据处理、画图分析,可以解决实验研究中的一些重要科学问题。
基于此,本文以电介质介电常数的测量实验为例,在掌握实验原理的基础上,采集记录实验数据,然后利用Origin软件分析处理实验数据。本文充分展示了如何利用科研数据分析软件来处理物理实验数据,同时也证实了将数据分析软件应用到大学物理实验课程中的可行性。
1 实验原理
介电常数是电介质材料本身的一个固有参数,描述了电介质对外加电场的响应能力。具体而言,在外加电场时,电介质会产生感应电荷从而削弱介质中的电场。因此,电介质材料被广泛应用在电容器以及电绝缘体中。本文主要分析固体电介质材料相对介电常数(εr)的测量。
实验利用电桥法测量固体材料的εr[6,7]。实验中电容极板的面积为S0,极板间距是D;电介质的面积是S,厚度为t。当以空气为介质时,测得的电容量C1为:C1=C0+C边1+C分1;当放入固体电介质时,测得的电容量C2为:C2=C串+C边2+C分2。其中,C边是固体电介质面积以外的极板电容量与边界电容之和;C分是测量时引线及系统引发的分布电容之和;C0是空气为介质、样品的面积S对应的电容量,C0=ε0S/D(空气介电常数近似为真空介电常数ε0);C串是指样品面积范围内的介质层电容和空气层电容串联所形成的电容量,C串=εrε0S/[t+εr(D-t)],变换公式可得,εr=C串t/[ε0S-C串(D-t)]。当两次测量中保持电极间距D和系统状态不变,则有:C边1=C边2,C分1=C分2,从而可得,C串=C2-C1+C0,将求得的C串带入以上εr公式可计算出固体电介质的相对介电常数。
在上面的实验中,空气的介电常数(ε≈ε0)不能直接测量得到,因此本实验另一重要的部分是采用线性回归法计算空气的介电常数以及系统分布电容[6,7]。利用以上测量系统,当以空气为介质,以面积S0的电容极板测得的电容量为:C=ε0S0/D+C分,通过改变极板间距D,可以测得对应的C。将该式与线性函数标准式y=A+Bx对比可以得到:y=C,x=1/D,a=C分,B=ε0S0。通过线性回归法得到的斜率可计算出ε0,得到的截距即为系统分布电容。在该过程中,利用Origin软件来科学分析是准确且有效的,这在接下来的数据处理中可以被充分证明。
2 实验数据测量及处理
2.1 实验数据测量
利用游标卡尺测出固体电介质样品的直径d,通过公式S=πd2/4可计算出电介质的面积S。利用螺旋测微器测出电介质的厚度t。电容极板的面积S0为2 161 mm2,极板的间距D定为5.000 mm。测出电极板间以空气为介质时的电容量C1,接着放入固体电介质,测出电容量C2。为减小实验误差,以上数据测量三次取平均值。表1中记录了测得的实验数据。
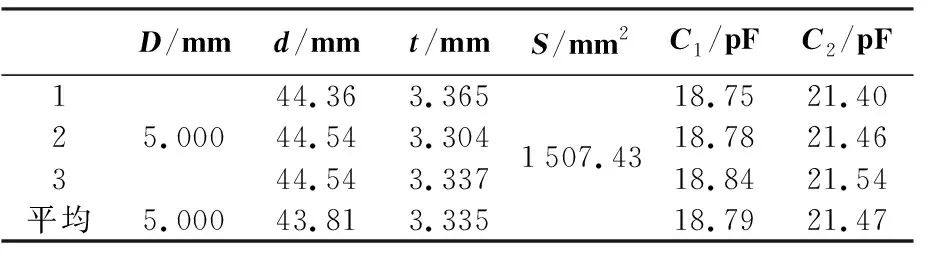
表1 固体电介质介电常数测量的实验数据及计算结果
接下来是测量计算空气介电常数和系统分布电容。按照表2中给出的极板间距逐渐增加电容极板的间距并测得对应的电容量,测量结果也显示在了表2中。

表2 空气介电常数和系统分布电容测量的实验数据
2.2 实验数据处理
将表2中的极板间距D和测得的电容量C输入Origin中,通过设置列的值得到1/D,然后将1/D作为x,电容量C作为y绘制散点图(图1)。接下来就是线性拟合这些散点。通过依次点击软件中的分析、拟合、线性拟合可以得到以函数y=A+Bx拟合的结果,如图1所示。结果显示,A是15.083,即系统分布电容为15.083pF。B是18.126,由实验原理分析中提到的B=ε0S0可计算出空气的介电常数ε0为8.388×10-3pF/mm,即8.388pF/m,这一数值与真空介电常数8.85pF/m非常接近。将ε0带入C0=ε0S/D得到C0为2.529pF,由C串=C2-C1+C0得C串为5.209pF,将以上结果带入εr=C串t/[ε0S-C串(D-t)]可得固体电介质的相对介电常数为4.374。
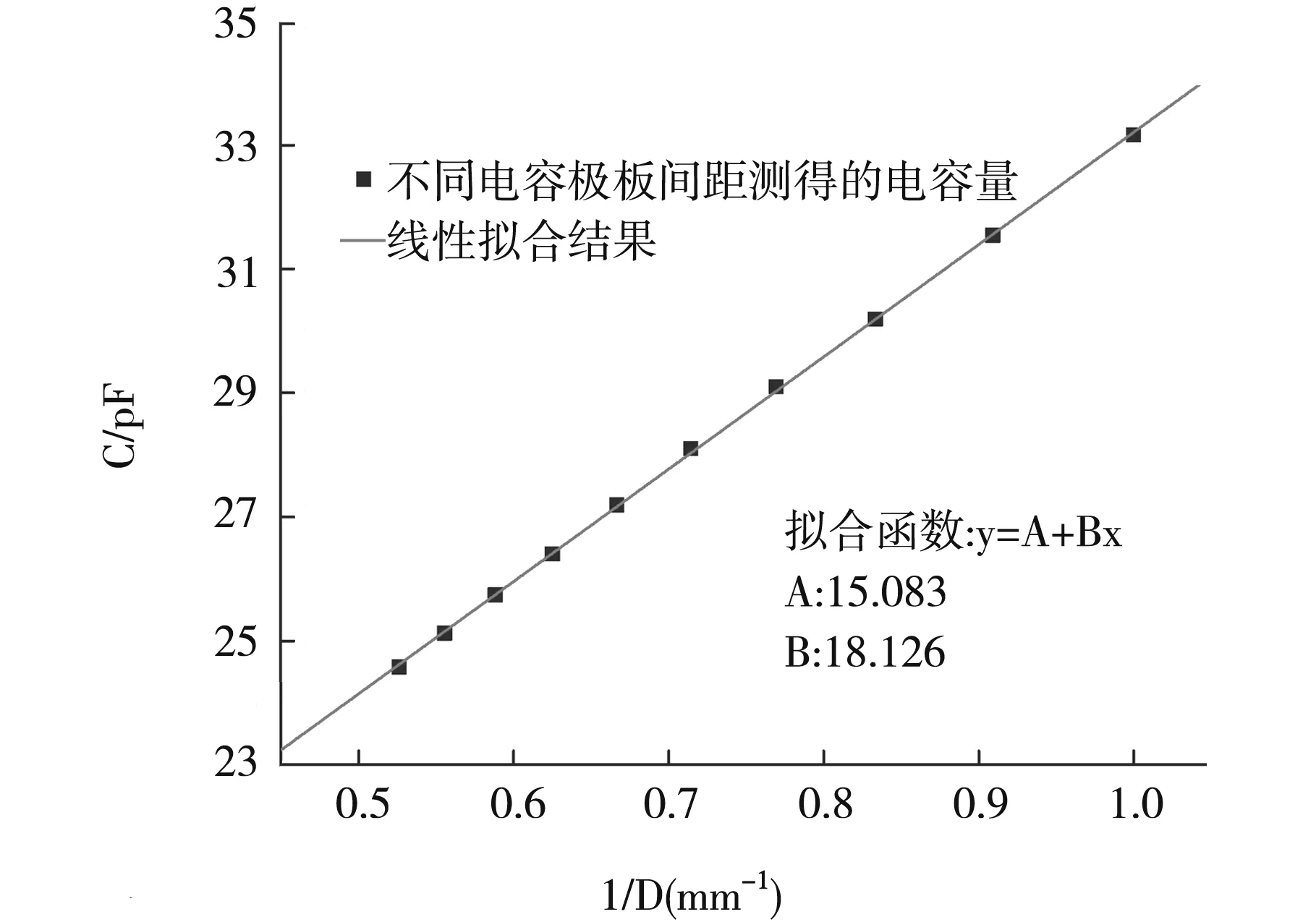
图1 不同电容极板间距时空气的电容量
以上分析表明,利用Origin进行物理实验数据处理是可行的。为了充分证明Origin处理实验数据较人工更准确、效率更高,我们按照传统的人工作图法处理了实验数据,得到空气的介电常数为8.654pF/m,固体电介质的相对介电常数是4.165,与Origin软件得出的结果存在一定偏差。这是因为人工拟合时,主要通过靠肉眼看从而将散点尽量集中在拟合线上或周围,所以结果准确度没有Origin软件拟合得到的高。此外,Origin软件处理以上数据只需要几分钟,大大节约了数据处理时间、提高了效率。
3 结 语
本文介绍了利用科研数据分析软件Origin处理大学物理实验中电介质介电常数测量的详细过程。将极板间距D和测得的电容量C输入Origin后绘制出以1/D为横坐标,C为纵坐标的散点图;以函数y=A+Bx拟合这些散点得到空气的介电常数为8.388pF/m,进一步计算得到固体电介质的相对介电常数是4.374。此外,我们还按照传统的人工作图法处理了实验数据,结果显示Origin软件处理的结果准确度更高,而且节约了数据处理时间。由此证实,利用科研数据分析软件处理大学物理实验的数据是可行的。本文详细列出了软件操作的过程,希望对学习用该软件进行实验数据分析的人员有借鉴作用。
