基于TPI数据的居民出行路径选择行为研究

2021-12-30孙秋霞赵术兰

重庆交通大学学报(自然科学版) 2021年12期

孙秋霞，张玉，赵术兰

(山东科技大学数学与系统科学学院，山东青岛 266590)

0 引言

出行者路径选择问题是交通领域内研究的热点问题，传统交通的出行路径选择行为研究，多基于确定性的环境进行建模分析。但实际上，由于城市交通系统受天气、道路运行状况等环境因素的影响，网络交通流呈动态随机变化，城市交通系统具有明显的不确定性。因此，研究不确定交通环境下的车辆择路行为，有利于出行者选择合理的出发时间及最优路径，为交通管理控制提出行之有效的解决措施和政策建议。

在不确定性环境的路径选择行为研究上，最早的路径选择行为模型假设所有的出行者都是理性的，具有相同的喜好、有完整的备选路径感知信息。即出行者可以随时获得路网上任一路径的客观信息，并能准确无误地计算出最短路径，并且所有的出行者对路径属性有相同的偏好。J. V. NEUMANN等[1]从逻辑和数学的角度出发，提出了理性人在不确定环境下的决策方法，即“期望效用理论”(expected utility theory, EUT) ，该理论认为在用户个人和备选方案既定的情况下，若以效用来描述备选方案的吸引程度，每个用户都会选择期望效用最高的备选方案，即“期望效用最大化假说”；在EUT理论的基础上，L. J. SAVAGE[2]又提出了随机效用理论(random utility theory, RUT)，认为备选方案的选择遵循主观效用最大化原则；C. F. MANSKT[3]提出的随机效用最大化模型(random utility maximization, RUM)，认为所有决策者都是“完全理性”的，并且总是选择其所认知到的选择方案中效用最大的方案。这些理论是基于用户对情景有完全了解的假设，并且在做出决策时绝对是理性的。显然，“完全理性人”的假设只是一种理想状态，与现实有较大差异。实际上，人们的行为、态度和偏好等并非完全是理性的，个人的行为通常受到他或她的个性、心理状态、风险偏好和环境等因素的影响。C. COLIN[4]进行的实验结果表明，关于个体绝对理性的假设在现实生活中并不成立；S. FUJII等[5]经实验发现出行者理性行为的观念不符合人的实际出行规划；因此，A. TVERSKY等[6-8]在“有限理性”的基础上提出了前景理论(prospect theory, PT)，将偏好引进，能有效解释不确定性条件下的决策行为。

鉴于前景理论能有效描述有限理性决策行为，在随后的研究中，赵凛等[9]在“前景理论”的框架下分析了先验信息条件下出行者的学习更新过程，建立了出行者路径选择的理论模型；赵凛等[10]基于“前景理论”，以两条平行路径的简单路网为例，从理论推算以及调查问卷等两方面，对一天内单次出行的路径选择行为进行了理论建模；田丽君等[11]假设路径的出行时间是某个区间数，且在区间数内的分布规律是均匀分布，推导综合价值函数和决策权重函数，进而构建最优路径选择模型，设计调查问卷并检验了模型的准确性；在模型参考点的设立上，D. KAHNEMAN等[6]基于前景理论给出了参考点的计算方式；赵凛等[9]采用路径自由流时间的加权平均、出行者的出行目的来确定参考点；黄中祥等[12]针对参考点计算公式中自由流时间不适用于拥挤路网的弊端,结合出行时间预算和有效路径的相关理论确立参考点；史国琪[13]基于出行时间预算和可靠性建立了考虑出发时刻的参考点模型，鉴于出行者可靠性不同，针对不同类型的出行者分别确定对应的参考点，进而得到出行时间的区间。

在研究出行者的路径选择方面，大多都基于路段仿真数据，给定备选路径的属性，构建路径选择模型[14-19]。部分学者将调查问卷数据用于构建模型，标定函数中的参数；但调查问卷数据成本高，不适应于所有出行者。大数据较调查问卷数据而言，覆盖范围广，种类多样，使用数据来构建模型，更有说服力。且在上述研究中，采用一个参考点，未考虑不同的情况下、不同的时间段下参考点的路径选择偏好。因此笔者基于前景理论，首先基于实测数据，综合行驶时间、红绿灯的等待时间设定参考点，构建路径选择模型；然后在不同时间段，随着参考点的变化，分析备选路径方案的选择前景值的变化情况；最后基于调查问卷数据对模型的结果进行验证。

1 前景理论

1979年D. KAHNEMAN等[6]提出的前景理论，是一种考虑个体偏好的不确定性决策理论。前景理论由价值函数和决策权重函数组成，价值函数取代了传统期望效用理论中的效用函数，决策权重函数替代期望效用理论中的概率。面对“收益”，出行者表现出“风险规避”，价值函数通常是凹函数；面对“损失”，出行者表现出“风险倾向”，价值函数是凸函数；对于损失的价值函数通常比对收益的价值函数更陡。

前景理论中由综合前景值来判定备选路径的偏好情况，即为：

(1)

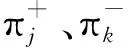
(2)

2 基于前景理论的出行者路径选择模型

2.1 参考点的设置

假设在一次出行中，从出发地到目的地有h条备选路径，lij表示为路径i第j条路段的长度，vij表示为路径i第j条路段的日平均速度。路径i出行时间ti由行驶时间与红绿灯的等待时间组成，即为：

ti=tid+tiw

(3)

式中:tid为路径i的行驶时间；tiw为路径i中红绿灯的等待时间。

2.1.1 行驶时间的计算

1)计算路径i第j条路段的日平均速度vij，再次根据路段与路径的包含关系，计算路径i的平均加权速度vi，即：

(4)

式中：q为第路径i包含的路段数目。

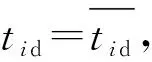
(5)

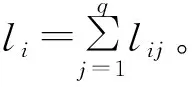
2.1.2 红绿灯的等待时间计算

因各路径中红绿灯个数不同，各路径的行程中红绿灯的等待时间tiw随之不同。假设出行者在一个路口的等待时间t′iw在区间[0,c]上服从均匀分布，路径i上所有红绿灯的等待时间tiw为：

(6)

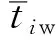
2.1.3 参考点的确立

出行者出行路径决策时通常会有一个理想出行时间tR，用来评价本次出行是“收益”还是“损失”，该时间称为路径选择决策的参考点，由赵凛等[9]提出的参考点的计算为：

(7)

结合式(3)，得：

(8)

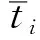
2.2 价值函数

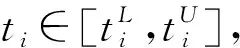
(9)

式中：α和β刻画价值函数曲线的凹凸程度，表示出行者在收益区域的“风险规避”特性以及在损失区域的“风险倾向”特性；λ刻画出行者的损失规避程度。当tR>ti时，出行者表现为“按时到达”，此时的出行者对本次出行感知为“收益”；当tR≤ti时，出行者表现为“迟到”，此时的出行者对本次出行感知为“损失”。

2.3 决策权重函数及前景值的计算

决策权重函数将行为偏好引入，用来刻画某一出行时间ti出现的概率做出的主观判断，采用D. KAHNEMAN等[8]提出的函数公式，即为：

(10)

(11)

3 案例分析

以山东省青岛市青岛大学到青岛站间的备选路径出行决策为例进行模型应用分析。青岛大学到青岛站间的两条备选路径重合率较小、清晰度较强、数据的可获取性较高，且在行程距离、等待红绿灯的时间、行驶时间波动程度等方面相差较大(图1)，可作为研究对象探讨出行者的出行偏好。两条路径的属性数据如表1。

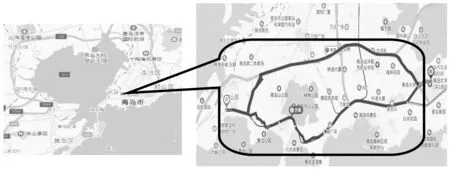
图1 山东省青岛市Fig. 1 Qingdao City, Shandong Province

表1 备选路径属性数据Table 1 Alternative route attribute data

3.1 数据获取及处理

1)从青岛市公安交通信息服务网上采集交通运行指数(traffic performance index, TPI)以及平均车速等数据；选取的时间为2018年9月工作日，共计19 d，数据区间为每天6:05—23:00、时间间隔为5 min。共计27 360条数据。

2)提取各路段TPI数据，由历史数据统计分析，划分出拥堵程度等级与TPI数据的对应关系：畅通(0～2]、基本畅通(2～4]、轻度拥堵(4～6]、中度拥堵(6～8]、严重拥堵(8～10]5种。根据对应关系将TPI范围不在(0～10]范围内的数据剔除掉。数据处理后，共获得19 380条数据。

3.2 备选路径前景值的计算

基于不同的时间段路径的流量不同，从工作日全天(6:05—23:00)、早高峰(7:00—9:00)和晚高峰(17:00—19:00)分析备选路径的偏好情况。备选路径数据由式(5)计算备选路径的行驶时间。假设红绿灯等待的时间服从[0,60]的均匀分布，由式(6)计算路径i的红绿灯等待时间tiw，最后再由式(8)通过对ξ进行赋值，得到不同时间段下不同的参考点tR。

计算得到的参考点如表2，从参考点的计算结果来看，全天、早高峰和晚高峰的参考点随ξ的变化而变化；时间价值系数ξ∈[0,1]，当ξ越大，表示时间价值越低，则期望本次出行花费的时间越长；早高峰和全天时间段内计算得到的参考点相同，晚高峰与前两个时间段计算得到的参考点不同。为了探讨在不同参考点下出行者对备选路径的偏好状况，根据不同时间段下的参数点取值分别设计全天、早高峰和晚高峰中的场景1和场景2。

表2 不同时间段下参考点Table 2 Reference points at different time periods

在式(9)价值函数中将α、β和λ分别取为0.88、0.88和2.25，将决策权重函数中的γ、δ分别取为0.61和0.69[6]，计算不同时间段内备选路径的前景值。

3.2.1 工作日全天的情况下

场景1：从出发地出发，出行者期望30 min内到达目的地，即参考点为30 min。

场景2：从出发地出发，出行者期望35 min内到达目的地，即参考点为35 min。

备选路径状况：

路径1：出行时间介于28～31 min的概率为100%。

路径2：出行时间介于21～28 min的概率是59%、介于28～35 min的概率为41%。

计算结果如表3。

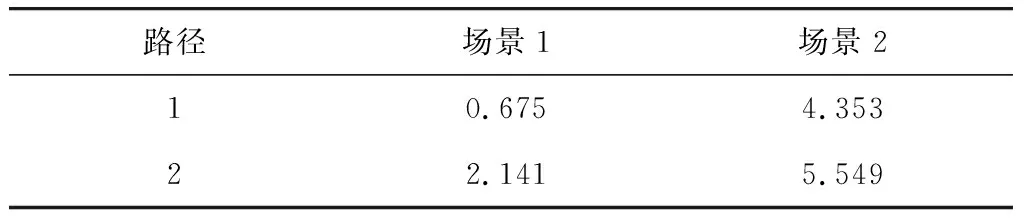
表3 全天时间段内备选路径的前景值(PV)Table 3 Prospect value (PV) of alternative paths inthe whole day time period

3.2.2 工作日早高峰的情况下

场景1：从出发地出发，出行者期望30 min内到达目的地，即参考点为30 min。

场景2：从出发地出发，出行者期望35 min内到达目的地，即参考点为35 min。

备选路径状况：

路径1：出行时间介于26～31 min的概率为100%。

路径2：出行时间介于21～28 min的概率为40%、介于28～35 min的概率为60%。

计算结果如表4。

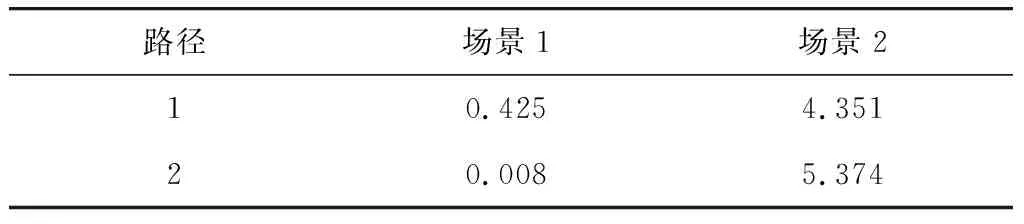
表4 早高峰备选路径的前景值(PV)Table 4 PV of alternative routes in morning peak hours

3.2.3 工作日晚高峰的情况下

场景1：从出发地出发，出行者期望26 min内到达目的地，即参考点为26 min。

场景2：从出发地出发，出行者期望32 min内到达目的地，即参考点为32 min。

备选路径状况：

路径1：出行时间介于25～30 min的概率为100%。

路径2：出行时间介于24～26 min的概率为60%、介于27～32 min的概率为40%。

计算结果如表5。

表5 晚高峰备选路径的前景值(PV)Table 5 PV of alternative routes in evening peak hours

通过以上3个不同的时间段，可以发现：

1)从备选路径的出行时间来看，早高峰和全天时间段内，出行时间划分区间相同，但所占比例不同；在晚高峰时，路径1和路径2的出行时间较前两个时间段有明显的差异，即路径1 的出行时间整体减小，路径2出行时间波动变小，这证明不同时间段内路径的交通流有较大差异。

2)在全天时间段和早高峰时段内，参考点相同，但备选路径偏好状况出现差异。全天时间段和晚高峰时段内，在场景1和场景2内，均为路径2的前景值大于路径1的前景值；但在早高峰的场景1时，路径1的前景值大于路径2 的前景值，这可能与不同时间段的交通状况有关，故导致不同时间段内，同一备选路径、同一参考点，却出现不同的结果。

3.3 参考点与路径前景值的变化关系

为探讨不同时间段内，备选路径的参考点与前景值的变化关系，改变最佳期望到达时间，观察路径1和路径2的前景值的变化趋势，具体见图2～图4。

从图2中可以得出，当以全天的数据为研究对象时，随着参考点的增加，备选路径的前景值也随之增加，路径2的前景值始终大于路径1，但两条路径的前景值之差先变大后逐渐缩小；在参考点为33.5左右，两条路径的前景值相差最小。这表示随着最佳期望到达时间的增大，出行者对备选路径偏好程度的判断能力逐渐减小，即出行者不易判断对路径的偏好性。

从图3中可以看出，在早高峰时，随着参考点的增加，备选路径的前景值也随之增加。在参考点小于29和大于35时，路径2的前景值总是大于路径1，这表明在此参考点区间内时，出行者更易偏好路径2；而在参考点介于29～35之间，对路径1的偏好大于对路径2的偏好，此时出行者更易选择路径1作为备选路径。证明在实际出行过程中，参考点设立的过大和过小，出行者更易偏好出行时间波动较大的路径，而在参考点处于[29,35]之间时，由于路径1的出行时间波动较小，在此区间内路径1“按时到达”的概率大于路径2，因此，出行者更易偏好路径1出行。

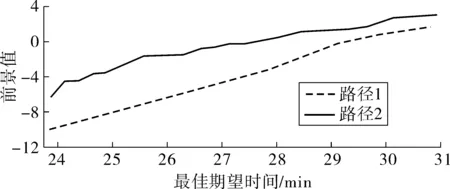
图4 晚高峰时段路径前景值与最佳期望时间的关系Fig. 4 Relationship between path PV and optimal expected time inevening peak hours

从图4中可以看出，随着参考点的增加，备选路径的前景值也随之增加，路径2的前景值始终大于路径1。两条路径的前景值之差逐渐减小；在参考点为30往后，备选路径前景值之差趋于恒定。

纵观3个图可以得出，随着参考点的增大，备选路径的前景值也随之增大，但前景值之差逐渐减小。证明在实际出行过程中，随着设立参考点的增大，路径1和路径2的前景值差距减小，对于在备选路径的选择上，更具有随意性。

在大多数情况下，路径2的前景值大于路径1的前景值，证明出行者在出行过程中更易偏好红绿灯等待时间较短、出行时间波动较大的路径，符合出行者出行中表现出“风险倾向”的特性。

4 基于调查问卷数据的模型有效性验证

根据备选路径属性，基于不同场景和备选路径，展开调查问卷，实际回收有效问卷264份，设计调查问卷内容包括个人基本信息以及路径选择。个人信息包括性别、年龄、学历、收入、家庭车辆拥有数、驾龄、日平均出行距离以及风险态度等。关于不同场景下备选路径的调查问卷结果如表6。

表6 基于调查问卷数据的统计结果Table 6 Statistical results based on questionnaire data

由表6可以发现，受访者调查问卷的结果与模型中最优路径选择结果选择一致，对调查问卷进行分析发现：在大多数情况下，路径2的前景值大于路径1的前景值，选择路径2的人数高于路径1的人数，证明了出行者在出行过程中更易偏好红绿灯等待时间较短、出行时间波动较大的路径，符合实际出行情景中，出行者会为了时间费用等问题倾向选择行程时间较少的路径。少数出行者选择出行时间稳定的路径。