高速公路改扩建施工期车辆强制变道持续时间研究
2021-12-30程金生张彦宁孟凌霄张立明
程金生,张彦宁,孟凌霄,张立明
(1. 中建山东投资有限公司,山东 济南 250101; 2. 同济大学 道路与交通工程教育部重点实验室,上海 201804;3. 中建筑港集团有限公司,山东 青岛 266031)
0 引 言
随着我国经济社会快速发展,交通需求也不断增长,一些早期修建的高速公路因设计标准偏低已经无法满足目前的交通需求。为解决交通需求与服务水平之间的矛盾,部分早期修建的高速公路正面临着改建、扩建问题。在满足路网交通运输需求的同时保证运营收益,高速公路改扩建通常采用边营运边施工的交通组织方式。施工过程中封闭车道、借用对向车道等措施使得车辆在进入施工路段前由原车道向未封闭车道强制变道,上述措施极易导致车辆发生追尾、侧向碰撞等交通事故,使高速公路改扩建施工路段成为事故黑点。为避免追尾、侧向碰撞发生,对高速公路改扩建施工期间车辆强制变道行为进行研究非常必要。
邹智军等[1]指出:强制变道是车辆为完成正常行驶目的而必须采取的车道变换行为。当车辆前方因道路改扩建施工或交通事故而封闭部分车道,车辆在目前行车道上继续行驶的路线遭到阻挡时,强制变道行为发生。为研究强制变道行为,学界提出了多种模型与方法。WENG Jinxian等[2]采用Logit模型描述了车辆强制变道行为,发现即便车辆存在很高的碰撞风险时,为在尽短时间内完成变道操作,驾驶员行为可能会变得激进。李玉洁等[3]采用元胞自动机分析了施工路段车辆变道点,认为最佳变道点与交通量有关且当车辆密度过高时换道成功率低。文献[4-5]也采用元胞自动机对变道行为进行了分析。
除变道概率、变道点之外,变道持续时间也是强制变道行为的重要特征之一。在文献[6-8]的研究中,变道持续时间定义为起始时刻到终止时刻所经历的时间长度。文献[6-7]认为:变道持续时间服从对数正态分布,变道持续时间为0.5~12.3 s;文献[8]认为:较长的延迟、距施工路段剩余距离更短、与目标前车TTC(TTC为自车与前车发生碰撞的时间)较短及目标车道的车辆速度较高等因素均可能使车辆变道持续时间变短。
生存分析是用于研究时间数据的统计建模方法,该方法将事件结果与其持续时间联系起来并能分析影响事件持续时间的因素。在交通研究中,生存分析可用于分析驾驶员违规操作间隔时间[9],行人过街时间等不同的时间数据[10]。吴江玲等[11]针对变道持续时间的特点,采用半参数生存分析方法对强制变道持续时间与车型、换道起点距施工路段距离之间的关系进行了分析,并得出了与文献[8]相似的结论。笔者也拟采用生存分析方法对高速公路改扩建施工期的车辆变道持续时间进行研究。
上述研究均分析了变道持续时间与车辆运动状态、交通状态之间关系,但施工路段线形等因素也会对行车安全产生影响[12-13]。笔者主要对强制变道持续时间与施工路段线形关系进行分析。
1 生存分析方法
1.1 变道持续时间及自变量定义
变道持续时间为起始时刻到终止时刻所经历的时间长度。变道开始点定义为车辆开始转向并进行变道操作时刻,变道结束点定义为车道变换到目标车道并回正方向时刻,变道特征点示意如图 1。
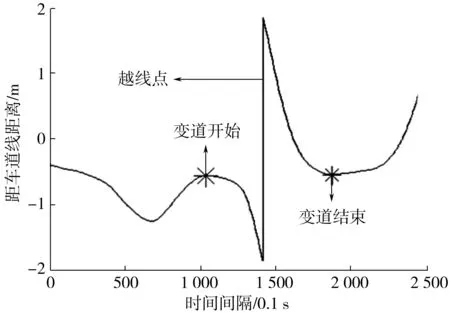
图1 变道特征点示意Fig. 1 Lane-changing feature points
1.2 生存分析要素
生存分析方法用于分析时间-事件数据,要素包括事件、事件生存时间t、事件结局δ、事件生存函数S(t)、事件风险函数h(t)。
1.2.1 事 件
本研究中事件时间起点为车辆开始转向并进行变道操作的时刻;事件终点为车道变换到目标车道并回正方向的时刻。
1.2.2 事件生存时间
事件生存时间t为强制变道的持续时间。
1.2.3 事件结局
事件结局δ表示车辆是否完成变道。当车辆完成变道时,δ=1;当车辆在整个观测时间内均没有完成变道时,δ=0。在本研究中,所有车辆均完成强制变道,故∀δ=1。
1.2.4 生存函数
变道持续时间生存函数S(t)表示在车辆开始转向并进行变道操作持续时间t后,其强制变道行为还未完成的概率,如式(1):
S(t)=P,T>t
(1)
1.2.5 风险函数
事件风险函数h(t)表明车辆开始转向并进行变道操作后,t到t+Δt时间内强制变道行为完成的瞬时概率,如式(2):
(2)
1.3 Log-rank统计检验
Log-rank统计检验是一种t检验,用于检验两个生存曲线之间是否存在统计显著差异。其原假设为两个不同生存曲线之间不存在显著性差异。假定有两组不同的时间-事件数据,需判断两个对应生存曲线之间的统计显著差异,Log-rank计算见式(3)、(4):
(3)
(4)
式中:Oi为第i组生存数据的观察分数;Ei为第i组生存数据的期望分数;mij为其中一组生存数据在t(j)时完成强制变道车辆数量的观察值;eij为期望值,j∈[1,N],N为延迟时间按照从小到大排列后的总项数;t(j)为第j小的时间数据。
笔者进行Log-rank检验时采用的生存曲线估计方法为Kaplan-Meier非参数估计方法。
1.4 Cox风险比例模型
Cox风险比例模型是一种半参数回归模型,常用于定量分析。其一般形式如式(5)。
(5)
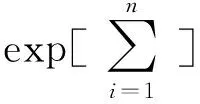
2 实验方案
2.1 实验设备
驾驶模拟实验采用同济大学驾驶模拟平台。驾驶模拟平台为拥有八向自由度的运动平台,驾驶舱内搭建250°环形屏幕和音响系统模拟实际驾驶的视听体验,舱内放置小型车实车并改装传感仪器进行数据采集。模拟平台可模拟各种交通环境,配合SCANeRTM软件能采集在各种交通运行状态下的的驾驶行为数据及车辆状态数据,数据采集频率为10 Hz。
2.2 实验环境
驾驶模拟实验路段基于山东省某高速公路进行设计。驾驶模拟实验路段为双向四车道、限速为100 km/h的高速公路,实验段全长10 km。为研究驾驶员面对因施工而封闭行车道时所采取的强制变道行为,实验设置了位于不同线形的施工路段。受实际高速公路线形限制、且为采集尽可能多的实验数据,实验段共设置了4个施工路段,施工路段位于左转圆曲线、直线段和右转圆曲线上(分类变量取值依次为1, 2, 3)。施工路段均按照规范放置了所需临时标志,路段所在圆曲线半径在2 800~4 400 m,封闭车道均位于超车道。
2.3 实验人员
驾驶模拟实验共招募16名驾驶员,驾驶员招募要求为拥有合法驾驶执照、超过实习期并有日常驾驶经验。驾驶员平均年龄25.6岁,标准差2.4岁,平均驾龄3.7年,标准差1.1年。
2.4 实验流程
强制变道指车辆为完成正常行驶目的而必须采取的车道变换行为。当车辆前方因道路改扩建施工而封闭部分车道、车辆在本车道继续行驶的路线遭到阻挡时,强制变道行为发生。
为研究驾驶员强制变道行为,实验中要求驾驶员在超车道行驶,当发现前方有因施工作业导致行车道封闭的情况,驾驶员发生强制变道操作。
3 实验结果与分析
3.1 变道特征点描述性统计
为表示强制变道行为特征,对变道起点、越线点和结束点的时距特征进行描述性统计分析,结果见图2。其中:时距指变道特征点距离改扩建施工路段上游过渡段起点断面的时距,负值代表特征点位于上游过渡段起点断面之后。
当施工路段位于左转圆曲线上时驾驶员发生强制变道行为的时间最早,距离上游过渡段起点的时距的平均值为6.31 s,车辆跨越车道分界线时间最早,距离上游过渡段起点时距的平均值为2.38 s。
当施工路段位于右转圆曲线上时驾驶员发生强制变道行为的时间最晚,距离上游过渡段起点的时距的平均值为4.42 s,车辆跨越车道分界线的时间最晚,距离上游过渡段起点时距的平均值为1.32 s。
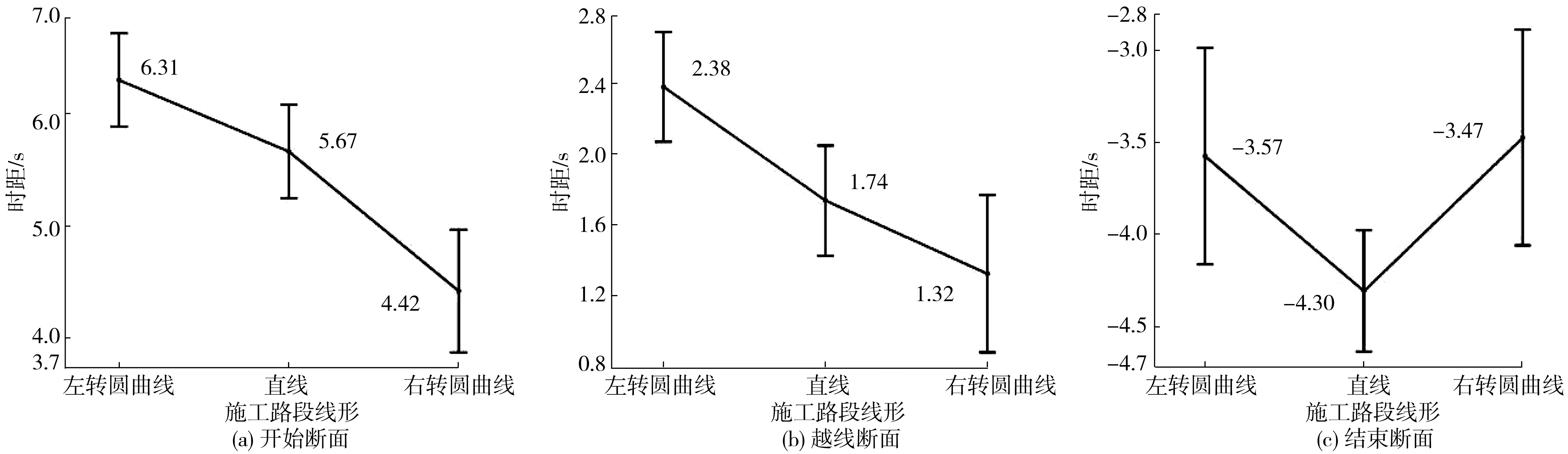
图2 各施工路段线形变道特征点时距Fig. 2 Time interval of lane-changing feature points for each construction section alignment
这3种线形条件下驾驶员完成变道时的时距均为负数,说明驾驶员在进入上游过渡段后才回正方向盘并在行车道内正常驾驶。统计结果表明:当施工路段位于右转圆曲线时,驾驶员强制变道行为发生在更靠近施工路段位置,更易发生交通事故。
3.2 变道持续时间生存分析
不同施工路段线形强制变道持续时间统计结果见表 1,生存曲线见图 3。

表1 施工路段线形统计结果Table 1 Statistical results of construction section alignment
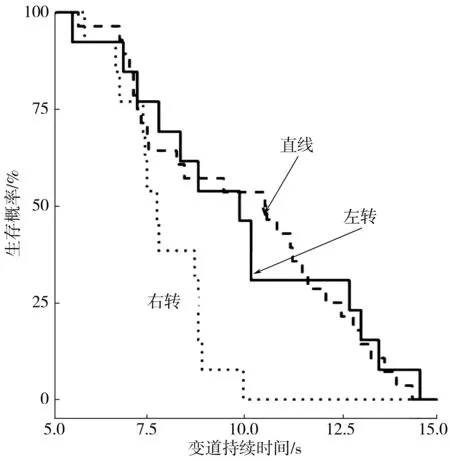
图3 各施工路段线形变道持续时间生存曲线Fig. 3 Survival curve of lane-changing duration foreach construction section alignment
统计结果显示:当施工路段位于左转圆曲线上时,车辆强制变道持续时间较长,为9.88 s;当施工路段位于直线段时,车辆强制变道持续时间为9.97 s;当施工路段位于右转圆曲线上时,车辆强制变道持续时间较短,为7.89 s。Log-rank检验的P值为0.006 0,说明不同施工路段线形强制变道持续时间在95%置信水平下差异显著。生存曲线结果表明:当施工路段位于左转圆曲线上时,有75%的驾驶员能在12.66 s内完成强制变道;当施工路段位于直线段时,有75%的驾驶员能在12.16 s内完成强制变道;当施工路段位于右转圆曲线上时,有75%的驾驶员能在8.81 s内完成强制变道。
生存曲线估计和Log-rank检验结果表明:施工路段线形显著影响驾驶员强制变道的持续时间。结合变道特征点描述性统计结果,当施工路段位于右转圆曲线时,驾驶员强制变道行为发生时车辆更靠近施工路段且行为持续时间更短,具有较大的安全隐患。
Log-rank检验结果和生存曲线说明了施工路段线形显著影响车辆强制变道持续时间,通过Cox风险比例模型分析线形与持续时间之间的定量关系,如表2。
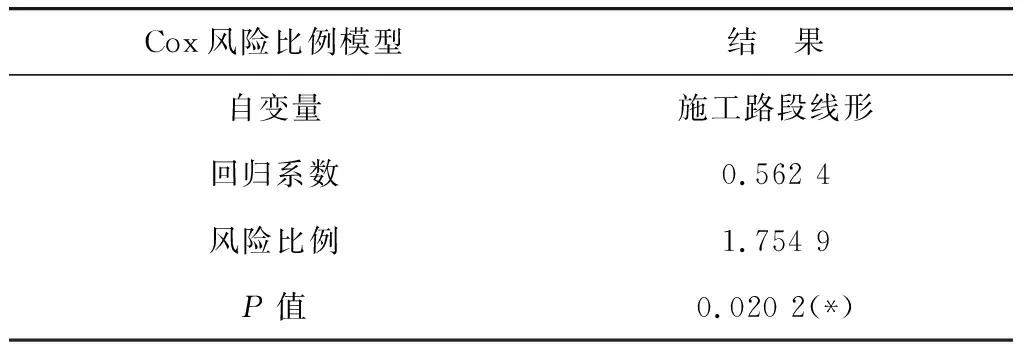
表2 Cox风险比例模型结果Table 2 Cox risk proportional model results
结果显示:施工路段线形回归系数为0.562 4,风险比例为1.754 9,即右转圆曲线施工路段相比直线施工路段、直线施工路段相比左转施工路段在时刻t时强制变道行为结束的瞬时概率高75.49%。当施工路段位于右转圆曲线时,变道持续时间相对较短,与Log-rank检验结果相符。
4 结 论
笔者基于模拟实验的驾驶行为数据,分析了强制变道特征点的时空分布特性;采用Log-rank检验验证了施工路段改扩建施工期间强制变道持续时间与施工路段线形之间关系;采用Cox风险比例模型进行了两者之间关系的定量分析。主要结论总结如下:
1)强制变道特征点的时空分布特性统计结果表明:当施工路段位于右转圆曲线时,驾驶员强制变道行为发生在更靠近施工路段的位置。这3种线形条件下驾驶员均在进入上游过渡段后才完成变道行为;
2)强制变道持续时间受施工路段线形的显著影响,不同施工路段线形之间的强制变道持续时间差异显著。结合变道特征点描述性统计结果,当施工路段位于右转圆曲线时驾驶员强制变道行为发生时车辆更靠近施工路段且行为持续时间更短,具有较大的安全隐患。图 4中的生存曲线的估计结果提供了不同情况下强制变道行为持续时间的75%分位数,可用于施工路段交通安全管理和布置方案设计;
3)Cox风险比例模型结果表明:右转圆曲线施工路段相比直线施工路段、直线施工路段相比左转施工路段在时刻t时强制变道行为结束的瞬时概率更高,并给出了施工路段所在线形与强制变道持续时间之间的定量关系。
笔者为解析不同施工路段线形强制变道持续时间变化趋势,其结果为改扩建施工交通组织管理提供依据。但研究过程中存在某些问题需进一步探讨:不同性别驾驶员的驾驶行为和对危险感知程度有所不同,因此驾驶员发生强制变道行为的判断可能有所差异。
