基于神经网络的无信号控制交叉口内车速预测模型对比

马莹莹，张子豪，吴嘉彬

(华南理工大学 土木与交通学院, 广东 广州510641)

0 引 言

城市道路平面交叉口是机动车、行人汇聚的区域，是城市道路交通网络的“咽喉”，同时也是交通冲突和交通事故的易发点。事故数据显示，我国发生在平面交叉口的交通事故约占道路交通事故总数的30%，联邦德国城市交通事故发生在平面交叉口约占60%～80%，美国发生在平面交叉口的事故数约占总事故的36%[1]。根据2015年世界卫生组织道路安全全球现状报告，全世界每年约有125万人死于道路交通事故，目前的趋势表明，若不采取措施，到2030年道路交通事故将上升为全球第五大死因。交叉口内车辆运行速度是车辆在交叉口内运行的重要交通特征，如果能够对交叉口内车速进行精确预测，对交叉口安全管理以及自动驾驶技术的发展都具有重要的支持作用。目前，关于交叉口内车速的研究主要分为两个方面，分别是对交叉口内车速的控制研究和预测研究。

在交叉口内车速控制研究方面，主要包括平面交叉口车速的控制方式和车联网环境下交叉口内车速引导控制，施晓芬[2]通过使用GPS记录车辆驶近交叉口及通过交叉口时的速度，并根据车辆在交叉口之前的行驶状态的不同，划分为畅行通行、停线通行和排队等待3种情况，总结了不同情况下车辆在交叉口内速度的变化规律；M. NEKOUI等[3]利用实地模拟的方式验证了车路协同环境下车速诱导的方式，可有效缓解不同种情况下车辆的紧急避让问题；M. A. S. KAMAL等[4]研究了车联网环境下多车道高效通行控制方法,并提出了针对部分车联网环境下的车速诱导控制；李鹏凯等[5-6]提出了面向个体车辆的车速引导机制与模型，并进行了仿真验证。

在车速预测研究方面，主要包括道路运行车速预测和交叉口内车速预测。楼挺[7]利用遗传算法改进的BP神经网络来预测道路运行车速，结果表明预测精度有所提高；王栋等[8]通过采集29个连续路段连续车速作为样本，利用BP神经网络对山区高速公路车速进行预测，预测精度高达93.3%；张良力等[9]利用车辆进入交叉口前的速度时间序列来预测车辆进入交叉口之后若干秒的速度值，从而来评估交叉口车辆碰撞风险；祝贺[10]以交叉口区域中车辆在直线路段的速度时序为模型，利用ARMA模型来完成对交叉口中心区域内车辆速度值的预测。

相比于传统的预测模型，神经网络具有更强的学习和适应能力，能够从众多影响因素中获取内在规律，具有很强的拟合非线性关系的能力[10]。徐嘉俊[11]将居民出行行为的显著影响因素作为模型的输入，利用遗传算法改进的BP神经网络来预测居民出行方式、次数和时间；颜秉洋等[12]通过交通流的周期性先验知识和残差数据训练ANFIS混合模型，进而得到交通流预测值。

综上所述，目前国内外在车速引导控制和道路运行车速预测方面已经做了比较多的研究，但在交叉口内车速预测方面的研究较少，并且以往对交叉口内车速预测是利用车辆进入交叉口之前速度的时间序列，来预测车辆的瞬时速度，并不能反应车辆通过交叉口的快慢程度，预测精度也不够高。基于此，综合考虑了影响车辆在交叉口内运行速度的因素，将车辆类型、车辆交通运行状态和运行环境等因素作为模型的输入，提出了一种基于神经网络的无信号交叉口内车辆平均速度的预测模型，并分别对深度神经网络(deep neural network, DNN)、BP神经网络、GA-BP神经网络和自适应模糊推理系统(adaptive neuro-fuzzy inference system, ANFIS)进行测试和预测性能比较分析。

1 数据采集及提取

1.1 观测地点

数据来自于广州市建设路-建设大道十字型交叉口，采用视频录像再进行视频识别与特征提取的方式收集数据。观测视频是在工作日、天气状况良好的情况下录制的，摄像头安装点为中环广场5楼，观测阶段为非高峰期，没有交通事故等特殊事件发生，该路口上游路段的限速为40 km/h。如图1，该交叉口的南北向道路是从北到南的单向双车道；东西向道路为双向通行道路，西进口有1条进口道和1条出口道，东进口有2条进口道和1条出口道。

图1 广州市建设路-建设大道交叉口Fig. 1 Intersection of Jianshe road-Jianshe avenue in Guangzhou

1.2 数据采集内容

研究的对象是车辆通过无信号控制交叉口中心区域的平均速度，通过主成分分析法，笔者初步筛选了以下几个影响因素：车辆类型、车辆通过交叉口的方式、车辆进入交叉口中心区域之前的速度、冲突方向车辆情况、冲突方向行人情况、驾驶员性别。

1.2.1 车辆类型

通过观察可知，所拍摄通过交叉口的车辆类型主要包括：小型车(小于7座)、中型车(8～17座)、大型车(17座以上)，在拍摄视频中，大型车主要是公交车。

1.2.2 车辆通过交叉口的方式

车辆通过交叉口的方式对进入交叉口中心区域的速度有很大的影响，按照通行方式的不同主要划分为：直行、左转、右转。

1.2.3 冲突方向车辆、行人情况

无论是直行、左转、右转的车辆，在交叉口内都会遇到冲突方向的车辆和行人，并且行驶速度会因此受到很大的影响，根据影响程度，主要分为3种情况：冲突方向无车辆(行人)、冲突方向有单个车辆(行人)、冲突方向有多个车辆(行人)。

1.2.4 车辆进入交叉口中心区域之前的速度

图2显示了车辆在交叉口区域内的方位，在文中，将图2中黄色矩形的区域定义为交叉口中心区域。车辆A在进入交叉口中心区域之前，驾驶员能观察到冲突方向是否有车辆和行人，并会做出加速或减速的判断，因此车辆在交叉口中心区域的速度与它之前的速度有很大的关系。如图2，车辆A在进入交叉口之前会驶过一段人行横道，将车辆经过这段人行横道的平均速度定义为车辆进入交叉口中心区域之前的速度(v1)，且v1=lbc/tbc，式中lbc和tbc分别代表车辆通过人行横道的路程和时间。

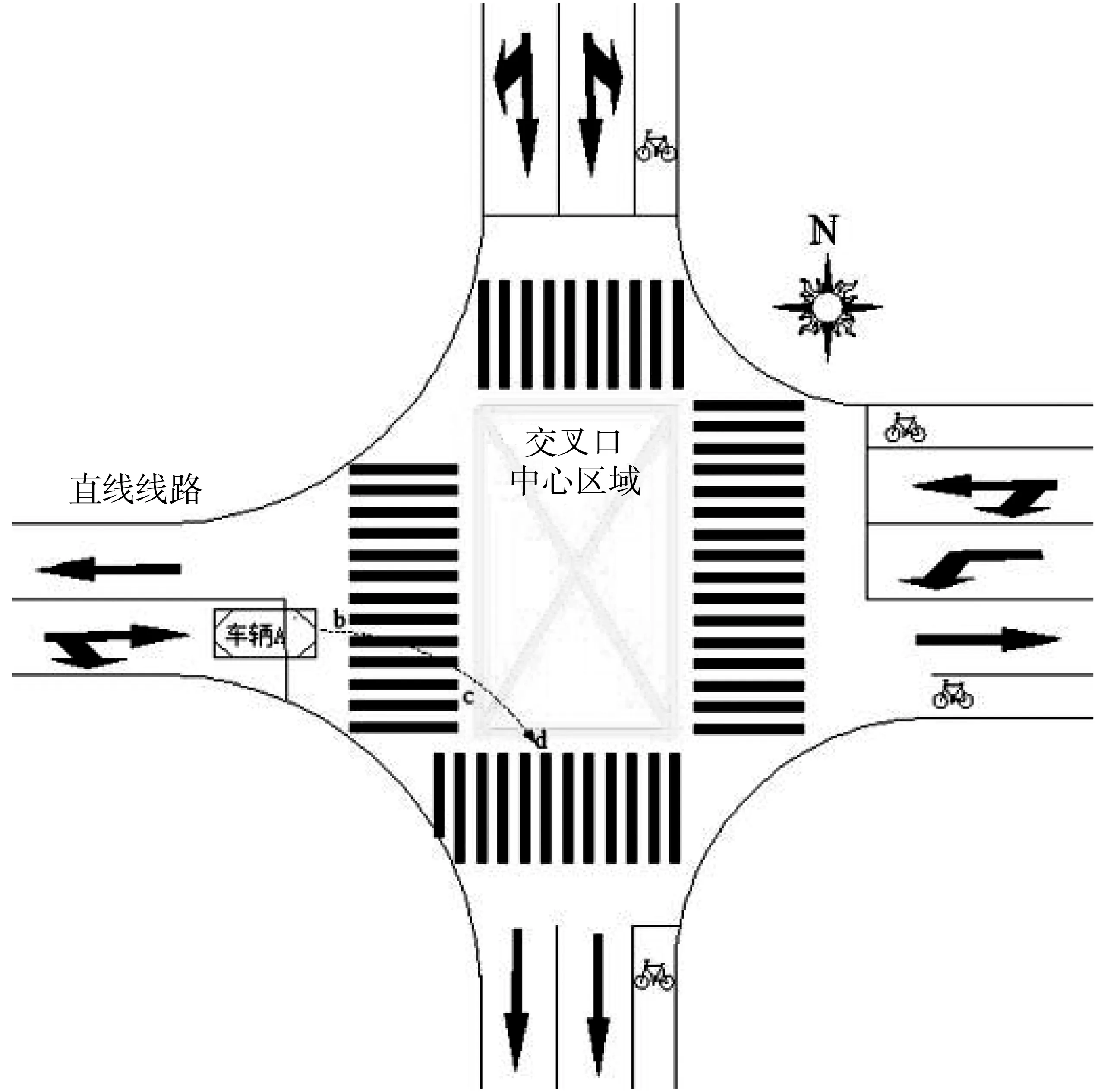
图2 交叉口区域车辆方位Fig. 2 Vehicle orientation in the intersection area

1.2.5 车辆在交叉口中心区域内的速度

把车辆在黄色长方形区域内运行的平均速度定义为车辆在交叉口中心区域内的速度(v2)，且v2=lcd/tcd，其中lcd和tcd分别代表车辆通过交叉口中心区域的路程和时间。

1.3 数据提取方法

通过观察拍摄的视频，可以直接获取车辆的类型、驾驶员性别和通过交叉口的方式，对于冲突方向的车辆、行人情况的获取，主要是根据车辆在通过人行横道的过程中，与该车辆行驶轨迹有冲突的方向是否有车辆、行人。而车辆进入交叉口中心区域之前的速度和在交叉口中心区域内的平均速度，采用基于视频的轨迹追踪分析软件tracker来获取，该软件可通过手动或自动的方式追踪研究对象的位置，实现对速度和加速度的覆盖和数据追踪。图3为采用tracker软件分析车辆运行轨迹的界面图。

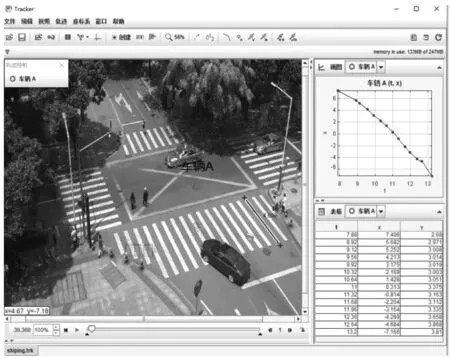
图3 车辆运行轨迹分析Fig. 3 Vehicle trajectory analysis

通过把所拍摄的视频导入到tracker中，设置好坐标轴和度量尺，采用手动的方式追踪研究车辆的位置，即可获得车辆在交叉口的运行轨迹。根据车辆运动轨迹图，可以计算出lbc和lcd，进而可以求出v1和v2，笔者总共提取了700份有效数据用于模型的训练和预测，为了列举所获取的数据，此处将v1和v2分为3类进行统计：<20 km/h，20～30 km/h，>30 km/h，表1汇总了在不同影响因素下车辆在交叉口中心区域内各类速度值的样本量。

2 预测模型构建

2.1 模型输入及输出变量标定

2.1.1 影响因素分析

对于影响无信号控制交叉口内车速的因素，初步考虑了车辆类型、车辆通过交叉口的方式、车辆进入交叉口中心区域之前的速度、冲突方向车辆情况、冲突方向行人情况、驾驶员性别。为了进一步确定这些因素是否为显著影响因素，利用SPSS软件进行Spearman相关系数分析，一般的相关性检验只要Sig值小于0.05，则认为两者具有显著相关性。根据表2的相关性分析结果，只有驾驶员性别这一因素的Sig值明显高于0.05，因此剔除该因素，其他5个影响因素的Sig值都小于0.05，即都为显著影响因素。

表1 不同影响因素下各类车速值的样本量Table 1 Sample size of various vehicle speed values under differentinfluencing factors 个

表2 交叉口内车速影响因素SPSS相关性分析结果Table 2 SPSS correlation analysis results of influencing factors of vehicle speed in intersection

2.1.2 模型输入及输出变量标定

建立的基于神经网络的预测模型的输入层神经元个数为5，由5个显著影响因素构成，输出层神经元个数为1，为车辆通过交叉口中心区域的平均速度。输入变量及数值标定如表3。

表3 输入变量标定Table 3 Input variables calibration

2.2 数据预处理

由于数据对网络模型的训练和预测效果有直接的影响，因此在进行训练之前要对数据集归一化处理到一个相同的范围内，从而使得所有数据处于相同的地位，避免输入输出数据数量级差别较大而造成网络预测误差较大。笔者采用最大最小值法将数据集归一化到[0,1]之间，函数形式为：

(1)

式中：xk为预处理之前的数据；xk*为预处理之后的数据；xmin为数据集中的最小值；xmax为数据集中的最大值。

2.3 预测模型网络训练

通过tracker软件共提取了700份有效数据，并利用sklearn库的train_test_split函数对有效数据进行分割，80%的样本用于训练模型，10%的样本用于验证模型，剩余10%的样本为测试数据集。其中，BP神经网络、GA-BP神经网络、ANFIS预测模型是利用MATLAB的神经网络工具箱进行模型训练，训练函数采用trainlm函数，目标误差设置为0.01，迭代次数设置为2 000次。深度神经网络预测模型是在python和Tensorflow计算条件下对模型进行训练，训练算法为随机梯度下降法，学习率设置为0.1，丢弃法值为0.5，迭代次数为2 000次。

2.4 预测性能评价指标

为了对比各个模型的预测效果，笔者使用的性能评价指标包括：均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)、平均百分比误差(absolute percentage error, APE)、nash-sutcliffe效率系数(NS)。其中，RMSE反映了预测数据和观测数据之间差异的样本标准差；MAE是用于评估预测结果与最终结果接近程度的度量；APE反映的是预测结果的误差程度，这3个性能指标衡量参数越小，表明模型的预测性能越好，而NS系数是通过将测量数据的方差与模型的拟合优度相关联来显示模型的效率，该值越大，证明模型的预测性能更好，具体公式如式(2)～式(5)：

(2)

(3)

(4)

(5)

3 预测模型测试

3.1 基于深度神经网络(DNN)的预测模型

DNN是属于人工神经网络ANN中的一种，它也是前馈神经网络，结构与多层感知器相似，相比于BP神经网络，它能够解决在隐藏层增多时，产生的过度拟合问题，有更强的学习和预测能力。笔者构建的基于深度神经网络的无信号控制交叉口内车速预测模型的隐藏层个数为3，具体结构如图4。

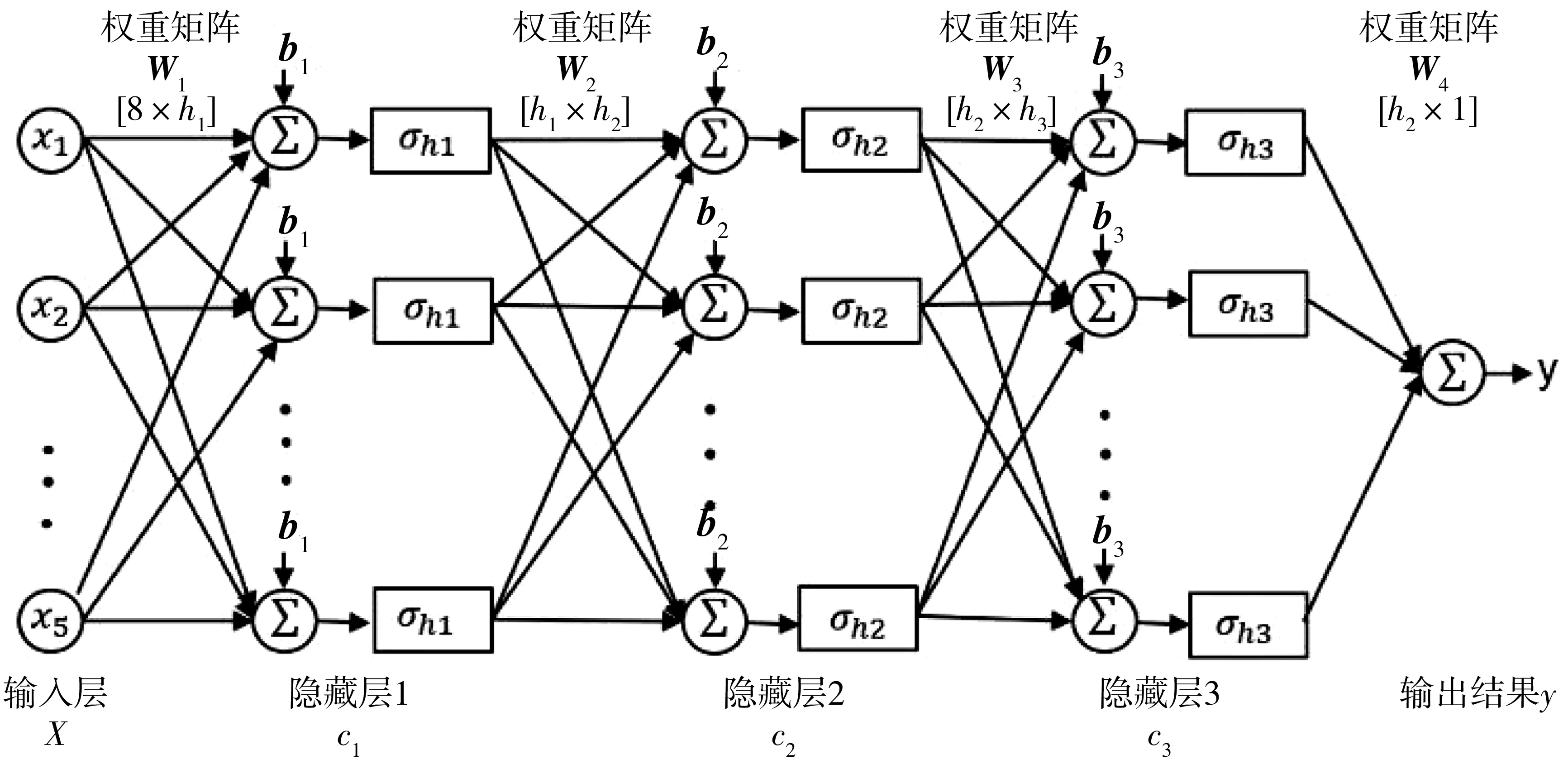
图4 深度神经网络结构Fig. 4 Structure of deep neural network model

在图4中，输入层神经元个数为5，x1,…,x5对应为影响交叉口内车速的显著因素；Wi为输出层和隐藏层对应的权重矩阵，即线性系数矩阵，bi为对应第i层隐藏层的偏置向量，ci为对应每一层的输出向量，该模型所采用的激活函数为Sigmoid函数，即：

(6)

因此，每个隐藏层的输出可以表示为：

c1=σh1(W1X+b1)

(7)

c2=σh2(W2c1+b2)

(8)

c3=σh3(W3c2+b3)

(9)

文中的DNN前向传播算法就是利用若干个权重系数矩阵Wi，偏置向量bi和输入变量X进行一系列的线性运算和激活运算，从输入层开始，一层层的向后计算，一直运算到输出层，得出输出结果值，最终输出的结果y为预测的车辆通过交叉口中心区域的速度值。

3.2 基于BP神经网络的预测模型

BP神经网络预测模型，具体结构如图5。

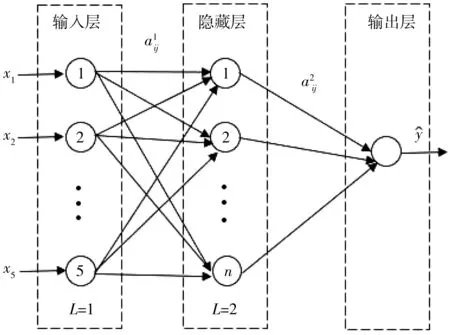
图5 BP神经网络结构Fig. 5 Structure of BP neural network

该模型的输入输出关系可以表达为：

(10)

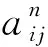
在确定了输入层和输出层的节点数之后，还需要选择合适的隐藏层的节点数，BP神经网络模型的预测效率与隐藏层节点数有很大的关系。目前，对于BP神经网络模型的隐藏层节点数的确定没有统一的方法，只能通过经验公式和多次实验来确定，本文参考的经验公式为：

(11)

式中：a为输入层节点数；d为输出层节点数；n为[1,10]之间的常数；L为隐藏层节点数。根据式(11)可以计算出隐藏层神经元个数为[4,13]，通过对样本的反复训练并比较得出：隐藏层节点数为6时，该模型的训练效果最佳，均方根误差最小。

3.3 基于GA-BP神经网络的预测模型

建立的GA-BP神经网络预测模型是在BP神经网络的基础上，对网络的权重和阈值进行改善。由于GA是模仿生物机制的随机全局搜索和优化方法，比较容易与其他算法相结合，使用遗传算法对初始网络的权重和阈值进行优化，可以改进BP神经网络的预测效果。其核心思想是：通过对初始值进行编码，用个体代表初始网络的权重和阈值，初始化网络的预测误差作为个体值的适应度，再通过选择、交叉、变异的步骤来获得最优的权重和阈值，具体过程如图6。

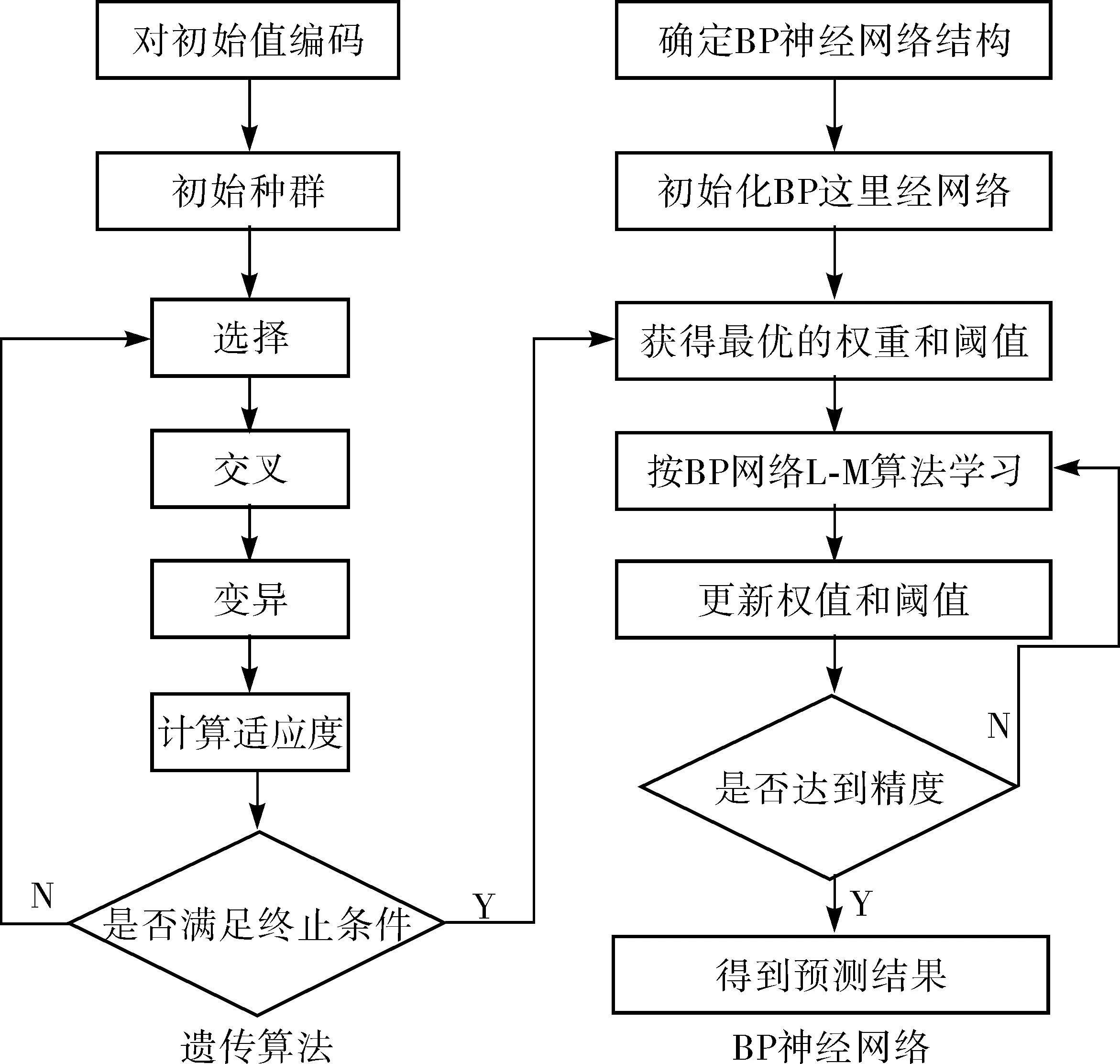
图6 GA优化BP神经网络流程Fig. 6 GA optimization BP neural network flow chart

第1步：编码种群初始化。GA优化BP神经网络训练时，可以使用两种编码方式：二进制编码、实数编码，采用的是实数编码。编码的实数串包括：输入层与隐藏层连接的权重和阈值、隐藏层与输出层连接的权重和阈值。建立的BP神经网络的层数为3，其中输入层节点数为5，输出层节点数为1，隐藏层节点数为6，因此编码的长度为5×6+6×1+6+1=43。

第2步：确定评价函数。BP神经网络预测模型的评价标准有RMSE、MAE、APE和NS，采用RMSE作为评价函数，当该评价函数达到最小值时，表明网络的权重和阈值得到了优化。

第3步：执行选择、交叉、变异运算。

第4步：用遗传算法优化得到的最优个体作为BP神经网络的初始权重和阈值。

第5步：执行BP神经网络训练过程，完成对车辆通过交叉口中心区域的平均速度的预测。

3.4 基于ANFIS的预测模型

自适应模糊推理系统也称为基于神经网络的自适应模糊推理系统，简称ANFIS，它是通过自适应的混合算法，在输入的数据中提取对应的模糊规则，从而来改善它的参数，最终获得最优解。建立的ANFIS预测模型的结构如图7。

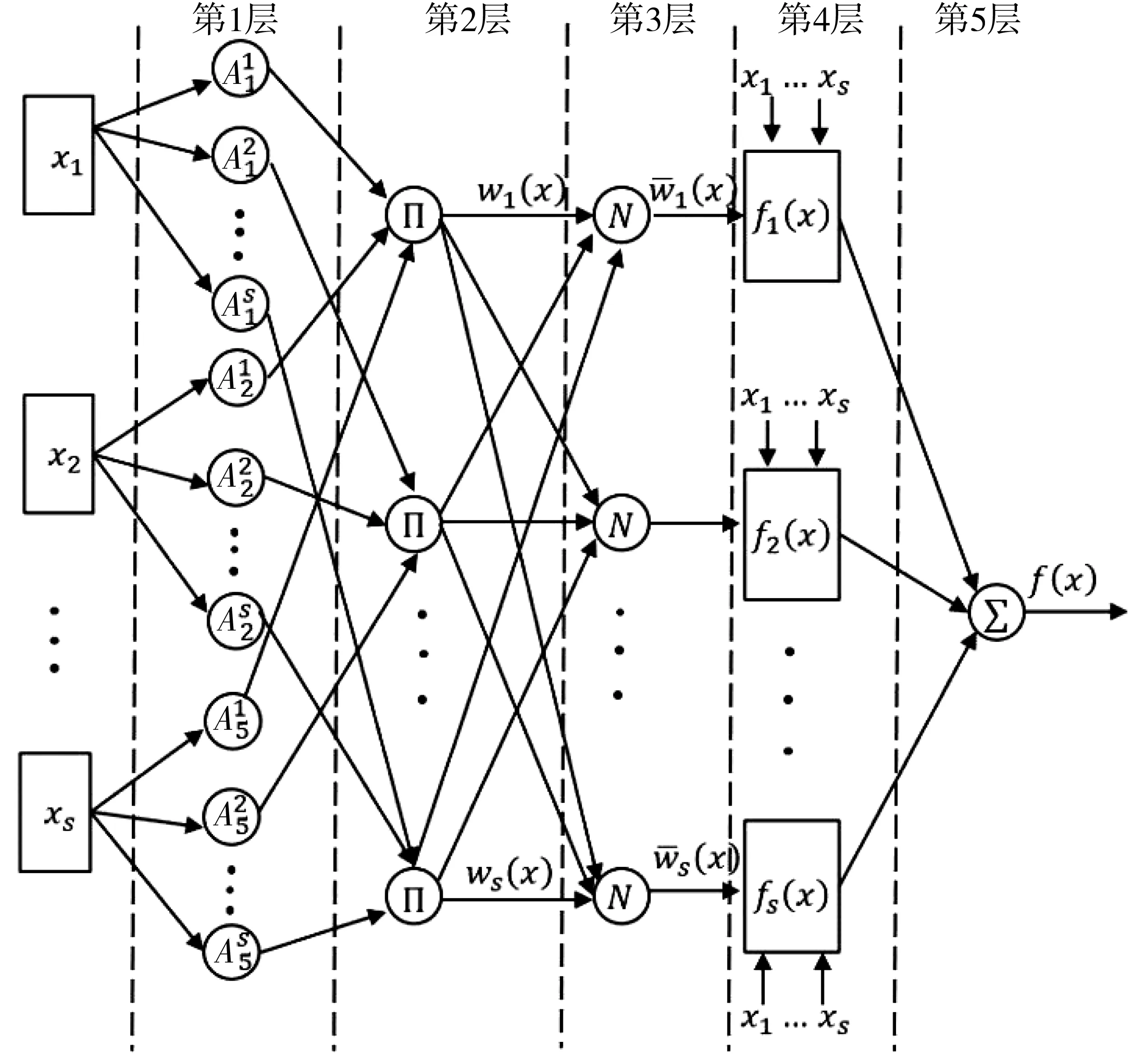
图7 ANFIS模型结构Fig. 7 ANFIS model structure

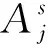
(12)

(13)

建立的ANFIS预测模型总共包含5层，第1层为模糊化层，它的作用是将输入的数据x1,…,x5，通过隶属函数输出为对应模糊集的隶属度，第2层主要是把前件部分的模糊集运算完成，并输出为对应的激励函数，第3层是把每个激励强度进行归一化处理，第4层是完成各个模糊规则输出的计算，最后一层是对该模型的输出进行计算。该模型的输入和输出可以用一个关系式表示为：

(14)

4 预测结果对比分析

4.1 预测准确率对比

笔者建立的4种模型预测结果如图8，其中左图为预测值与实际值的对比，右图为预测模型在测试集上的准确率随着迭代次数的变化；表4为预测模型在训练集和测试集上的准确率。由此可以看出：①深度神经网络预测模型在训练集上的准确率为90.63%，测试集上的准确率为94.44%，预测效果是4个模型中最好的；②利用GA改进的BP神经网络在训练集和测试集上的准确率都有提升，并且迭代次数没有增多；③ANFIS预测模型的迭代次数是4种中最多的，预测精度最低，即计算代价最大，因此该模型的效果最差。

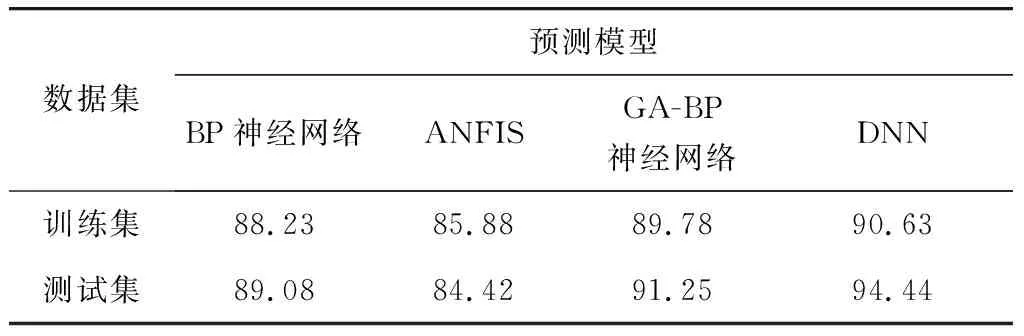
表4 各个模型预测准确率Table 4 Prediction accuracy rate of each model %

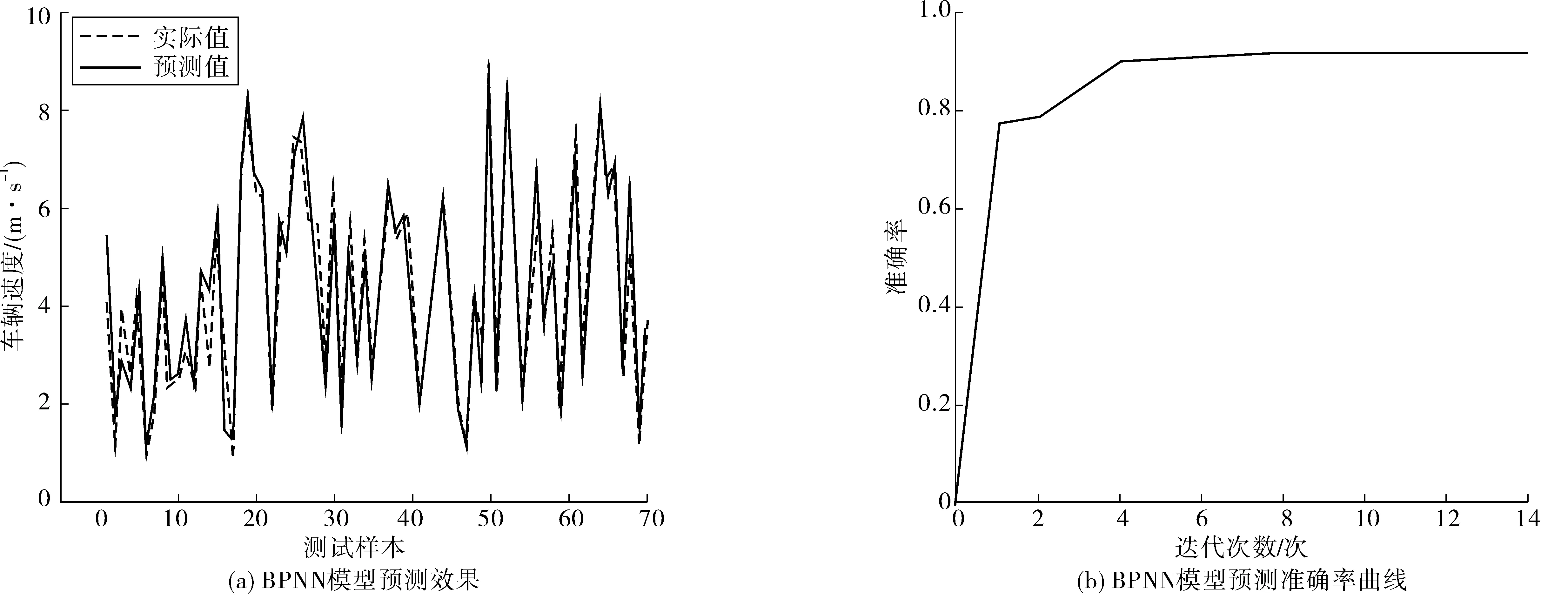
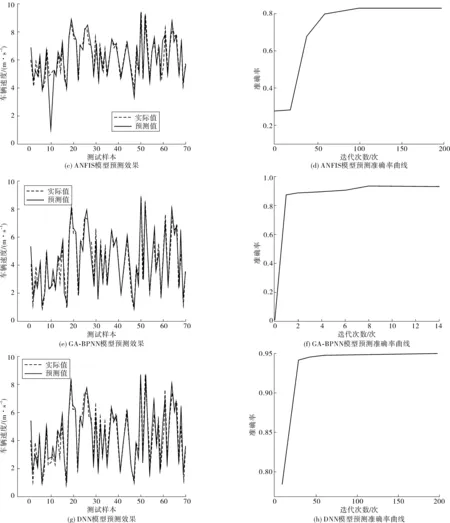
图8 4种模型预测结果Fig. 8 Prediction results of four kinds of models

4.2 性能评价指标对比

根据预测结果，分别计算4种预测模型的性能评价指标值，具体结果如表5。其中，基于深度神经网络预测模型的RMSE、MAE和APE是最小的，nash-sutcliffe效率系数NS是最大的。由此可以看出：在考虑多个显著影响因素来预测交叉口中心区域内车速的问题上，深度神经网络的预测效果最好，其次为GA-BP神经网络、BP神经网络，而ANFIS在该问题上的预测性能较差。

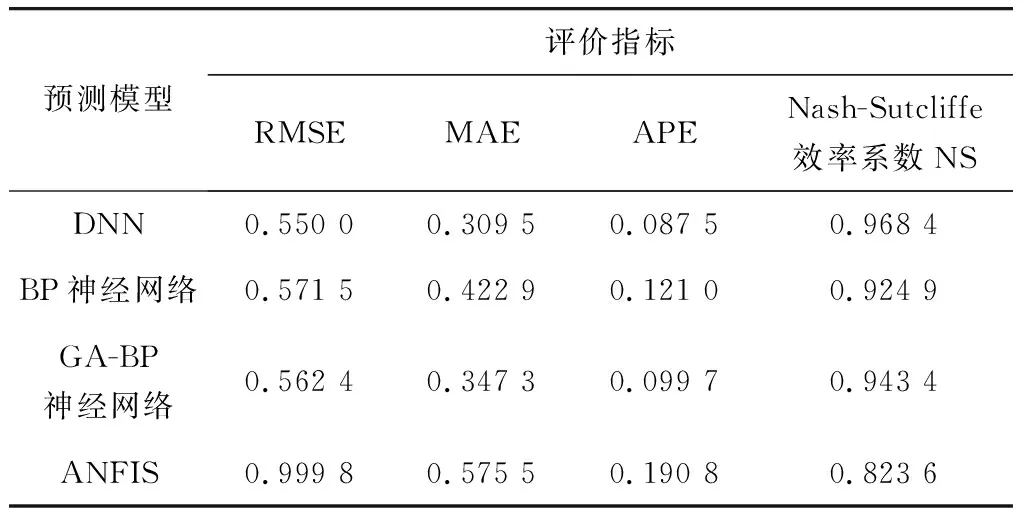
表5 4种预测模型性能评价指标值对比Table 5 Comparison of performance evaluation index values offour kinds of prediction models

5 结 语

针对无信号控制交叉口中心区域内车速预测问题，有别于以往只考虑车辆进入交叉口之前的速度时间序列，筛选了对它有显著影响的因素，分别为：车辆类型、车辆通过交叉口的方式、车辆进入交叉口中心区域之前的速度、冲突方向车辆情况、冲突方向行人情况，建立了基于神经网络的预测模型，并利用4种网络进行测试。

预测结果表明：4种模型都适用于车辆通过交叉口中心区域内平均速度的预测，但DNN具有更好的预测精度和泛化能力，利用GA改进的BP神经网络预测精度在训练集和测试集上都有提高；由于笔者只考虑了一个无信号控制交叉口，并且样本量有限，在今后的研究中，将把交叉口的几何类型、信号控制方式等因素考虑进去，建立更为全面的样本库，进一步分析不同因素的影响程度，并在现有的预测模型上逐步改进，进一步提高预测精度。