繁星无法超越——三体问题溯源

邵瀚雍

(北京师范大学 物理学系，北京 100875)

在科幻小说《三体》中，作者构建了一个特殊的恒星系统：某行星系中有三颗质量不等的恒星，在彼此的引力下相互作用，而该行星系的文明则位于3颗恒星附近的一颗行星上. 因为恒星无规则的运动，这个行星上的文明饱受摧残. 一开始他们试图预测恒星运动的规律，但每次的尝试都以失败告终. 他们转而决定逃离行星系，奔向地球.

这个难题在1900年的第一次世界数学家大会上就已经被提出了. 著名数学家希尔伯特(Hilbert)在会上提出了23个困难的数学问题；与此同时，他特别谈到了两个经典的完美数学问题，其一是我们熟知的费马猜想；其二便是N体问题. 这个问题要求人们给出在已知质量和初始时刻坐标、速度的N个质点在彼此引力作用下的后续运动规律.

1 三体溯源：数学家的尝试

事实上，三体问题有着深刻的数学和物理背景. 作为经典力学的主要创立者，牛顿在研究万有引力定律时，就已经基本解决了最简单的两体问题，并预测了双星系统运动规律.

合理外推是科学探索的核心理念之一：当人们知道一元二次方程的通解，就会自然而然地思考一元三次方程的通解；当人们知道两体问题的解时，也会思考三体乃至N体问题的通解，而日-地-月系统正是我们最熟悉的三体系统之一. 作为外延，牛顿首先探讨了3个天体在引力作用下的运动系统演化问题，也就是上述N=3时的三体问题[1].

颇为可惜的是，即使聪明如牛顿，至临终前也没有给出任何进一步的解答. 从物理上讲，这个问题并不复杂，但是它对数学的要求很高. 在牛顿生活的17世纪，微积分学才刚刚被创立不久，当时人们的数学水平远远不能解决这个复杂的物理问题. 于是，这个悬而未决的问题又被拖了整整100年之久，等待着下一位数学家来解决.

1772年，拉格朗日(Lagrange)和他的导师欧拉(Euler)接下了研究三体问题的火炬. 他们首先开始考虑研究限制性的三体问题，在这个问题中，一个天体的质量被忽略不计，而只受到其它两个大天体的引力作用而运动. 作为数学分析创始人之一的拉格朗日，他通过一系列严密的计算，求出了这个限制性问题的后两个特解(前3个为欧拉所求得). 这个5个解正是我们熟悉的拉格朗日点[2].

拉格朗日点，又称平动点，是指当一个小物体在两个大物体的引力作用下，可以在空间中找到一点，在该点处，小物体相对于两大物体基本保持静止. 拉格朗日点的发现，对于三体问题的求解有着巨大的意义：人们至少看到了希望的曙光. 相应的，人们在天文发现中也证实了拉格朗日点的确存在.

在图1的5个拉格朗日点中，有两个拥有良好的稳定性，人们可以发射航天器稳定在拉格朗日点，这样航天器就可以利用两个天体的引力达到相对静止的状态，比如詹姆斯·韦伯空间望远镜(JWST)就处在日-地系统的第二拉格朗日点. 除了宏观三体系统的引力场内存在拉格朗日点外，也有人发现类似的点电荷电场中也存在类拉格朗日点[3].

图1 三体系统中的拉格朗日点

自拉格朗日点发现以后，人们对于三体问题的研究又停滞了近100年之久，直到某次机缘巧合，才让这个被遗忘已久的问题又重新回到了人们的视野中.

1889年，瑞典与挪威的国王奥斯卡二世(Oscar Ⅱ)要准备自己的60岁大寿. 而奥斯卡二世在大学期间对数学很感兴趣，对科学研究也很支持，于是资助创办了《数学学报》杂志. 为了这次贺寿，身为《数学学报》主编的米塔格·列夫勒建议，设立一个竞赛，让人研究太阳系是否稳定. 而这正是一个N体问题的变式. 此前的天体力学家虽然有过繁杂的计算，但是仍然无法解决小分母问题. 当年拉普拉斯通过计算证明了太阳系的稳定性，但是他只能后推900年，对于几十亿年龄的太阳系来说，这不过是弹指一挥间，难以真正回答这个问题.

竞赛公告的第一段是：“具有任意多个质点的系统，其中任何两点间的作用力满足牛顿定律，在任意两个点不发生碰撞的情况下，试给出每个点的坐标，这个坐标可以以时间的某个已知函数作为变量的级数表示，并且对于所有的取值，该级数是一致收敛的. ”

在这个时候，一位在数学领域造诣极高的数学家接下了火炬，他正是庞加莱(Poincaré). 他的研究领域涉及数学、物理和天体力学，并被公认为是19-20世纪之交的领袖数学家.

图2 庞加莱像

在这次公开悬赏之前，庞加莱已经凭借自己在自守函数论和微分方程等方面的工作而被人们公认为世界一流数学家了.1883年，29岁的庞加莱发表了第一篇天体力学方面的论文；一年之后，他又发表了第二篇关于天体力学的论文. 奥斯卡二世的这个问题进一步激发了庞加莱对这个天体力学问题的兴趣.

1885年，庞加莱开始集中精力研究三体问题，此时距离竞赛截至日期还有大约3年时间. 庞加莱先采用了希尔研究月球时所采用的模型，但经过不断坚持与搁置的循环尝试后，他终于理清了方向. 1887年，庞加莱发现这个问题不能用牛顿、拉格朗日与拉普拉斯等人所采用的小参数展开等传统方法解决，而必须改换一个新的思路.

庞加莱首先考虑了较为理想的情况，也就是我们熟知的限制性三体问题：一个尘埃漂浮在两个巨大天体形成的体系里，应该如何预测尘埃的轨迹. 在计算机尚未出现的时代里，他依靠惊人的计算能力，绘出了尘埃前期的运动轨迹. 当他试图在纸上画出那些轨迹的时候，他写道：“这难以画出来的图形的复杂性令我震惊！”.

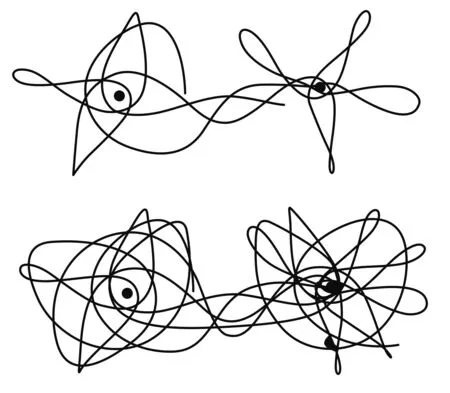
图3 复杂的尘埃轨迹示意图

随后，庞加莱另辟蹊径，独自发展出一套方法：微分方程定性理论. 他开始尝试运用渐近展开与积分不变性的方法，定性研究小尘埃的轨迹[5]，并且深入研究了小尘埃在同宿轨道和异宿轨道(相当于奇点)附近的行为. 但是在研究过程中，庞加莱发现，尘埃的轨迹几乎不可能被预测. 经过整整三年的努力，他认为这个问题无法完全解决，并随后把自己的研究成果寄到论文评审委员会，还在论文开头写了一句[6]：“Nunquam praescriptis transibunt sidéra fines”(繁星无法超越).

尽管庞加莱并没有完全满足奥斯卡二世给出的要求，也没有完全解决N体问题，但他长达160页的论文仍然令评审团的三位数学大师兴奋无比. 他们认为庞加莱对三体问题的研究取得了重大突破：太阳系的相对稳定得到确认.

魏尔斯特拉斯(Weierstrass)在给杂志主编的信中写道：“请告诉您的国王，这个工作虽然不能被视为对所求问题的完整解答，但是它的重要性使得它的出现将标志着天体力学的一个新时代的诞生. 因此，陛下预期的公开竞赛的目的，可以认为已经达到了”. 于是国王高兴地把奥斯卡奖——一枚金质奖章和2500瑞典克朗，授予了庞加莱.

3 夜幕降临：三体问题无解

对于三体问题，人们希望能找到一个长周期(哪怕这个周期非常长)或者是一个解析解(收敛的级数解)来描绘三体运动的规律. 但是，庞加莱证明了三体问题的解析解是不可能存在的.

这个由简单的代数表达式和积分给出的三体运动微分方程没有通常意义上的解析解，并且，除特殊情况外，3个物体的运动是不重复的. 在一般三体问题中，每一个天体在其他两个天体的万有引力作用下的运动方程都可以表示成3个二阶的常微分方程(如图4所示)，或6个一阶的常微分方程. 因此，一般三体问题的运动方程为18阶方程，必须通过18个积分才能得到完全解. 然而，目前还只能得到三体问题的16个初始积分，还不能解决三体问题[7].

其实，早在 1887 年，勃隆斯(Bruns)就证明了三体问题中质点的速度和位置无法用函数定量表达. 几年后, 庞加莱进一步证明了位置、速度和质量比的关系无法用定量的解析式表达.

除了解析解不存在之外，数值解的情况也不容乐观. 为了得到具有意义的数值解，计算机往往需要进行长时间的工作. 早在20年前，就已经有对于N体问题进行数值解的研究了，但是效果不佳[8].

并且，即使可以通过现代的量子计算方式极大加快计算进程，也难以避免三体系统的一个核心问题：误差. 在进行数值分析的过程中，计算机往往会近似估计相对的高阶小量，或因为计算机的数字尺度限制，无法进行完整的数据迭代. 短时间内也许看不出什么区别，但是随着时间的积累，数值计算所得到的结论可能与真实情况差别极大.

除了宏观世界中存在的天体引力系统外，人们也研究过微观世界中氦原子核与两个电子根据库仑定律相互作用的三体系统，不过依然不能精确求解出氦原子核的运动规律[9].

不过在最近的科学研究中，借助于计算机的高速发展，已经有许多文献找到了不少N体问题运动的特解，如图5和图6，这些解十分优美[10].

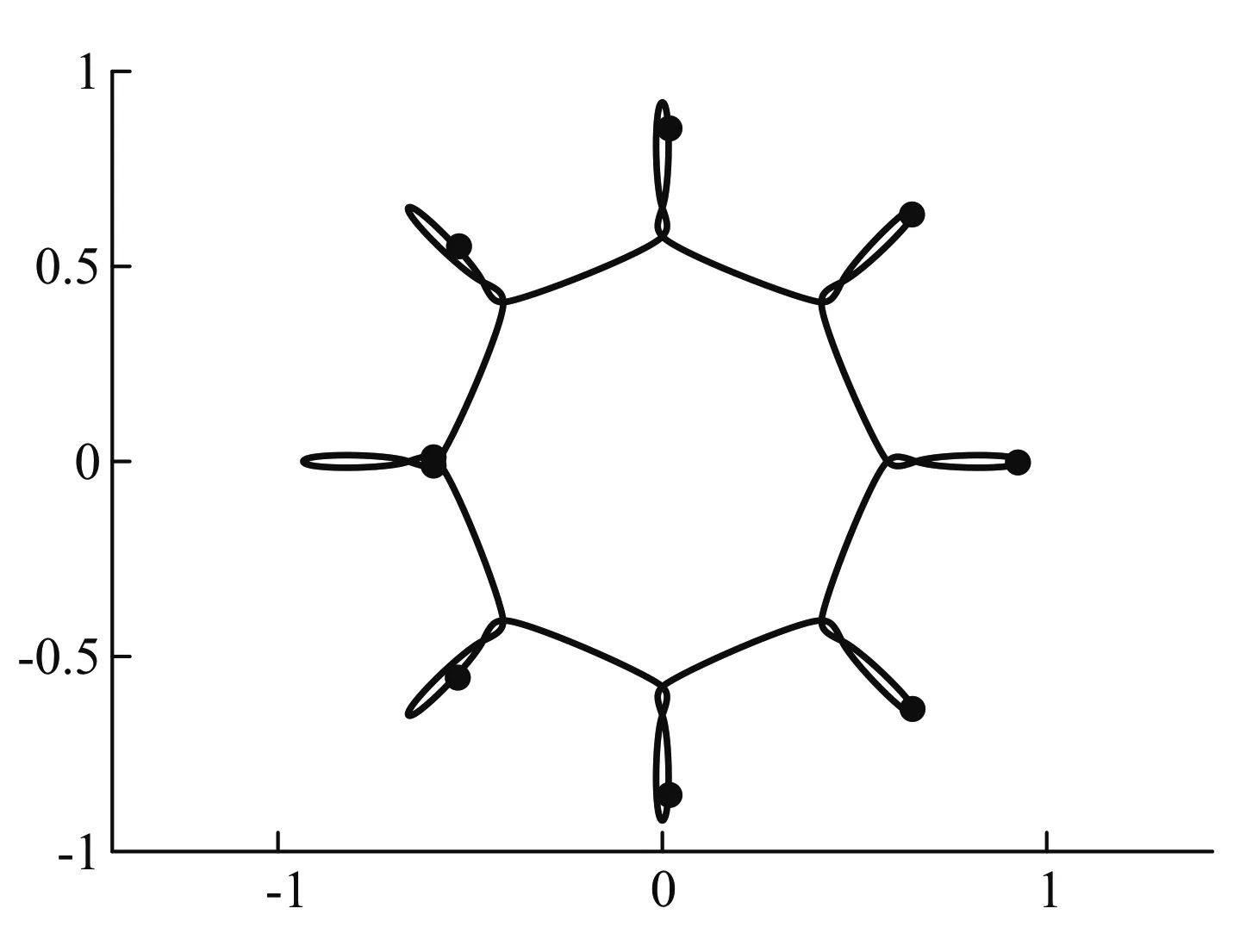
图5 N=8时的特解

图6 N=9时的特解

4 夜空星光：混沌理论创立

在庞加莱证明了三体问题的无解性后，他并没有停下这个工作. 在研究这个问题的时候，他第一个敏锐的发现了这种运动规律不循环的、对初始条件敏感的行为，并着手研究这类型的问题. 这类问题被他统称为混沌(Chaos).

庞加莱首先考虑了二维平面内的动力学问题，并提出了一个重要的定理，即庞加莱—本迪克松定理[11]. 该定理由庞加莱提出，并由本迪克松给出了完整的证明过程.

如果一个二维动力学系统内运动连续可微，且动力学流在一个区域内封闭，而区域内也没有定点，则该区域的动力学流将收敛于一条闭合轨道.

这个定理指出，在有限的二维系统内，物体的运动形式只有两种，要么归于平衡态，要么满足周期运动. 换言之，庞加莱指出了二维系统中并不存在混沌行为. 图7是在进行节拍器同步过程中自由度为1.5的相平面轨迹，可以明显看出有一个定点(平衡态)和一个较弱的闭合轨道.

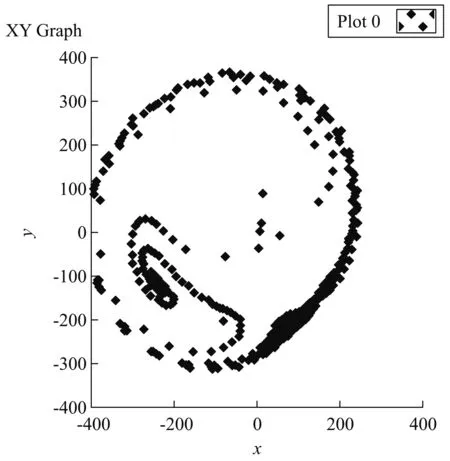
图7 节拍器同步过程中的相平面轨迹图

不过，由于庞加莱所处时代的数学限制，他的研究只是指出了运动的非线性方程所造成的动力系统的非线性. 尽管如此，他对于三体问题的研究也为后者研究混沌系统打下来理论基础.

在庞加莱之后的很长一段时间，非线性动力学还是停留在非线性振子等比较基础的问题上.直到20世纪60年代初，美国的气象学家洛伦兹(Lorenz)在使用计算机进行气象问题研究时，发现了“确定性非周期流”. 他的研究指出，气候对初始条件的变化极为敏感，且不同的条件会导致不同的演化轨迹，从而大大增加系统的不确定性. 他将之通俗的比喻为“蝴蝶效应”[12].

与此同时，1971年，人们开始研究湍流问题的纳维-斯托克斯方程

此时发现湍流解的形式也存在奇异吸引子的情况[13]，这与之前庞加莱的研究结果很相近，而湍流问题也正是一种困扰人们多年的混沌系统.

随着混沌、分形和分岔理论的不断完善，多数学者认为，混沌系统内有3个重要的特殊情况[14]：

1) 系统对初始条件极其敏感，哪怕是最初状态的轻微变化或是微小的误差都能大幅度改变结果的形态，这直接导致混沌系统无法被预测. 如图8，这是一个两面弧形的球桌，我们把球的初始方向从虚线改变为实线，可以发现其运动轨迹完全不同.

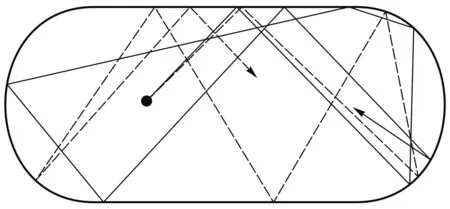
图8 小球运动轨迹示意图

2) 系统内部存在分形的情况. 分形意味着系统在不同的标度下有着自相似的性质，并且系统可以产生具有结构和规则的难以发现的有序模式.如图9所示，这是限制性三体问题中尘埃在10个不同的初始条件下，所演化的10条不同轨道的分形结果，但这个看似无规则的轨迹有着一定的自相似性.

图9 尘埃运动轨迹的不同分形结果

3) 系统内存在奇异吸引子. 吸引子，是系统被吸引并且最终固定为某一状态的性质. 一般来说，吸引子分成三种：点吸引子、极限环吸引子和混沌吸引子. 前两者一般是收敛的，而奇异吸引子则不同，它可以使系统偏离收敛性的吸引子，而改变系统的状态，增加系统的不可预测性. 图10是由Python绘出的洛伦兹(奇异)吸引子的示意图.

图10 洛伦兹吸引子示意图

非线性还表现在许多别的方面，除了经典的混沌情况之外，系统也可能会出现多稳态的情况，这表示系统有可能在两个或多个不同的互斥状态之间不断切换，这也是非线性的表现之一. 除此之外，非周期振荡、孤立波等现象也不断被发现.

随着人们对非线性方程研究的不断加深，非线性系统正在作为一门崭新的学科指引人们前进的道路. 有的学者认为，混沌理论是继相对论和量子力学之后本世纪的第三次科学革命. 由此而生的非线性物理也有着许多的分支学科. 这其中包括了非线性动力学、非线性声学、非线性光学和量子混沌学等许多新兴学科.

6 结语

在人类为了三体问题而奋斗的几百年里，虽然结果是让人有些失望的，但是中间的过程是精彩而又值得铭记的. 费马猜想就被叫做“会生金蛋的鸡”，其原因正在于人们在证明的过程中诞生的种种珍贵的思想和方法.

而作为另一只下金蛋的“鸡”，三体问题已经为人类生下了不少珍贵的方法和理论. 时至今日，人们对于三体问题的兴趣仍然没有衰减.

2013年，贝尔格莱德物理研究所的物理学家发现了等质量、零角动量的三体问题的13族特解，正式将特解扩展为16族[15]. 2017年，上海交通大学的廖世俊研究小组利用超级计算机，找到了三体问题的600多个新的周期解家族. 如图11所示的几个周期解[16].

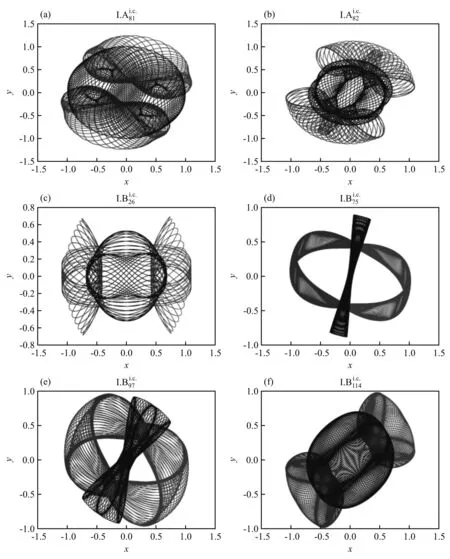
图11 新发现的一些周期解家族

除了对周期解的研究之外，在探寻数值解的道路上，为了达到高精度和长时间的预测，有学者已经尝试改用数值积分的方式，通过神经网络来进行机器学习，以达到预测轨迹的目的[17].