应用一种多核稀疏表示模型实现掌纹分类

尚 丽,周 燕,孙战里

(1. 苏州市职业大学 电子信息工程学院, 江苏 苏州 215104;2. 安徽大学 电气工程与自动化学院, 安徽 合肥 230039)

1 引 言

稀疏表示(sparse representation,SR)是在超完备字典空间内,用少数原子的线性组合来表达大部分或者全部的原始信号,这样就可以大大减少计算量,节约存储空间,目前已在数字信号处理、图像处理及模式识别等领域被广泛应用[1～3]。虽然采用SR模型已成功实现人脸图像分类[1],但这种模型不适用于具有相同方向的不同类数据,即使是线性可分时,分类效果仍旧不明显。主要原因是特征基正则化后具有相同方向的数据存在重叠显现[1,2],因此基于SR的分类方法的应用范围受到限制。如果在SR模型中引入一个合适的核函数,即基于核函数的SR(kernel based SR,KSR)模型[4～7],则可以解决上述问题。通过核变换可以把原坐标系中线性不可分的问题转化为投影空间内线性可分的问题[3～5],可以有效处理高维输入,并且使得在高维空间中的SR提高识别率和判别性能[7～10],因此一些基于单核的分类方法陆续被提了出来并被用于图像的特征分类[4～7]。由于不清楚选择哪种核函数最适合具体分类任务,所以考虑结合几种核函数就很有意义。Huang H C等将基于多核的方法应用于聚类问题,已取得了较好的结果[1,8～11]。

本文结合多核函数[8～11]和KSR的优点[12～16],提出一种基于多核的稀疏表示(multipile kernels based SR,M-KSR)模型,并在多核映射空间内采用具有二次约束的最小二乘化优化方法训练稀疏系数[8,11,14],同时考虑多核权重系数和图像残差之间反比的关系来更新权重系数,最后应用所提出的基于M-KSR的特征分类方法在PolyU掌纹数据库上验证了该方法的有效性。

2 核函数及多重核的提出

2.1 核函数的定义和作用

机器学习中常遇到学习非线性模型的情况,使得非线性不可分的问题转化为线性可分的问题。常用的做法是通过某非线性变换函数φ(·),将变量z所在的输入空间Γ映射到1个高维特征空间H,即使得Γ中的变量z能够通过φ映射得到H空间中的点h:h=φ(z)。若对所有的z,q∈Γ,存在1个函数κ(z,q)满足式(1)条件[1,2],则称κ(z,q)为核函数。

κ(z,q)=φ(z)·φ(q)

(1)

式中φ(z)·φ(q)为φ(z)和φ(q)的内积。显然,核函数是映射关系φ的内积,并没有增加维度的特性。但是,可以利用核函数的特性,构造能够增加维度的核函数。比如,由二维映射到三维,数据区分就会更容易,这也是聚类、分类中常用到核函数的原因。尤其是近几年,随着核函数在支持向量机的成功应用[3,4],出现了更多的基于核的方法,例如核主成分分析、核Fisher判别分析、核SR方法等。概括地说,利用核函数或者核技巧,可以使得原本在低维空间线性不可分的数据集,在足够高的维度中存在线性可分的超平面,从而解决数据非线性可分的问题;另外,利用核函数也可以省去高维空间里的繁琐计算,甚至可以解决无限维空间无法计算的问题[6～8,17]。

2.2 多重核的提出

核函数的选择要满足Mercer定理,常见的核函数有高斯核函数、线性核函数、多项式核函数、径向基核函数、Sigmoid核函数、B样条核函数、张量积核函数等[11～13]。但是在具体应用时,单个核函数往往不是最合适的核,因此基于多个核函数结合的方法被提出[3,8,14]。给定M个定义在ΓP×ΓN上的Mercer函数κm(·,·),P为每一样本的维数,N为样本个数,则对样本xi和xj构造如下的多重核函数：

(2)

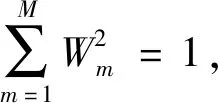
(3)

由式(3)知,对样本y来说,映射函数φ将原空间的数据映射到一个高维多重核空间Γ′中,即y在Γ′空间内的像为：

φ(y)=[φ1(y),φ2(y),…,φP(y)]T

(4)

3 核稀疏表示分类

3.1 稀疏表示分类

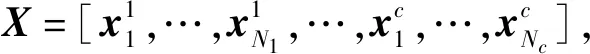
(5)

(6)

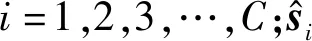
3.2 基于核的稀疏表示分类(K-SRC)

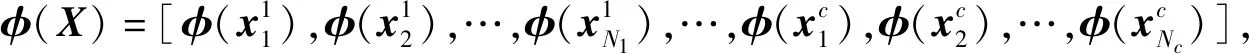
(7)

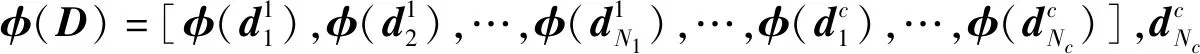
Ek(S,D,y)=φ(y)Tφ(y)+STφ(D)Tφ(D)S-

2φ(y)Tφ(D)S=

K(y,y)+STK(D,D)S-

2K(y,D)S

(8)

式中K(·,·)∈ΓN×N为核函数κ(·,·)的半正定Gram矩阵;K(D,D)和K(y,D)可由式(9)计算。

(9)

根据式(8),在核空间内,类似SRC方法,根据样本重构最小误差实现测试样本的分类。

4 多核稀疏表示学习

4.1 M-KSR的优化目标

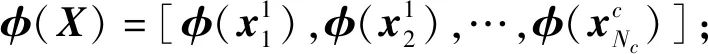
(10)

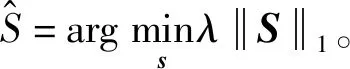
(11)

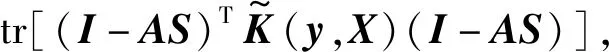
(12)

则多核函数表达式为：

W1κ1(u,v)+

W2κ2(u,v)+

W3κ3(u,v)

(13)

显然,多核函数的性能和所选用的单核函数的权重系数有关。

4.2 M-KSR的优化目标

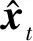
(14)

引入核关系后,式(14)改写为：

i∉Lt

(15)

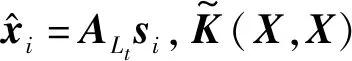
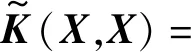
(16)

则第t步稀疏系数更新规则为：

(17)

固定稀疏系数S,则训练原子字典的目标函数为：

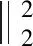
(18)

对式(17)关于ai求导并引入核关系则得到ai的更新规则：

Δai=-2siφ(X)[φ(y)-φ(X)aisi]=

(19)

当学习完稀疏系数后,第m个核函数对应的残差rm计算如下：

(20)

5 多核函数权重选择和M-KSR分类(M-KSRC)

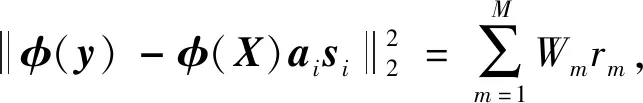
(21)

式中权重系数Wm和残差rm成反比,当残差较大时,权重系数就要调小,反之,权重系数则要调大。

结合第3.2节的K-SRC法和第4.2节的M-KSR学习规则,多核稀疏表示分类的算法归纳如下：

3) 根据式(17)和式(19)更新稀疏系数向量si和原子向量ai;

4) 根据式(20)计算第m个残差rm,并根据式(21)更新权重系数Wm;

6 实验结果与分析

6.1 特征提取

测试图像选自香港理工大学PolyU掌纹数据库中的100个人的600幅掌纹图像[18]。每1幅图像原始大小为284×384像素,所提取的矩形感兴趣区域为128×128像素。选择每个人的前3幅图像作为训练图像,后3幅图像作为测试图像,每1幅图像转化为一个列向量,则训练集合Xtrain和测试集合Ytest的大小均为1282×300像素。为了减小计算量而不影响特征提取的精度,采用小波变换把每一幅掌纹图像处理成64×64像素,则训练集合和测试集合的大小为4 096×300像素。为了进一步减少核空间内的计算量,本文首先采用主分量分析(principal component analysis,PCA)法进行降维分析[14,18],得到的前16个特征基图像如图1所示;然后在不同的PCA维数下采用极端学习机(extreme learning machine,ELM)、径向基函数神经网络(radial basis function neural network,RBFNN)和距离分类器进行特征分类,从而确定核空间内较合适的主分量个数。分类结果如表1所示,可以看出,主分量个数越多,采用ELM分类器得到的特征识别率越高,但是对另外2种分类器却不符合这种趋势。当主分量个数小于256时,3种分类器的分类结果基本相同。但是,当主分量个数大于256时,ELM分类器的优势则非常明显。综合考虑计算量和分类效果,我们最终选择主分量的个数为324,这样用于SRC、K-SRC和 M-KSRC 算法的输入集合大小为324×300像素,算法计算量被有效降低,可以加快特征寻优速度。

图1 PCA的前16个特征基图像Fig.1 The first 16 feature base images of PCA

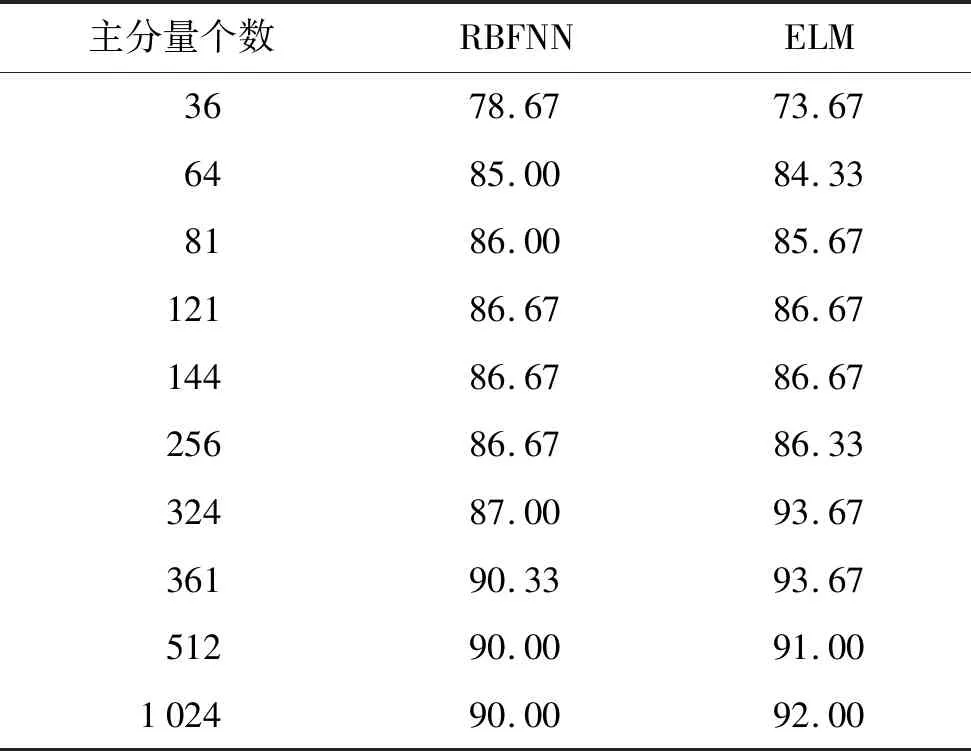
表1 不同主分量个数下特征分类结果(PCA算法)Tab.1 Feature classification results of the different number of principal components (the PCA algorithm)(%)

6.2 特征分类

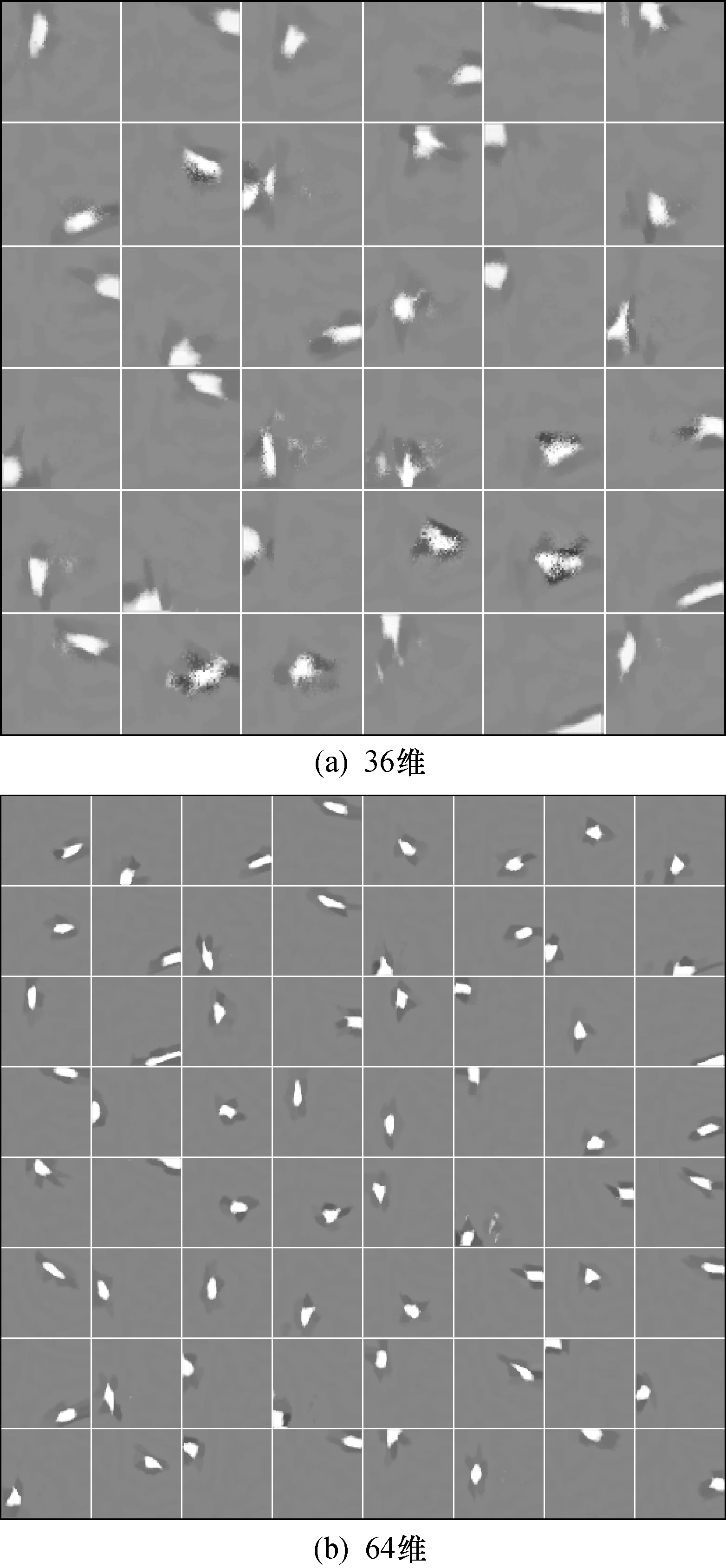
图2 M_KSR算法得到的不同维数的特征基图像Fig.2 Feature base images with different dimensions obtained by the M_KSR algorithm

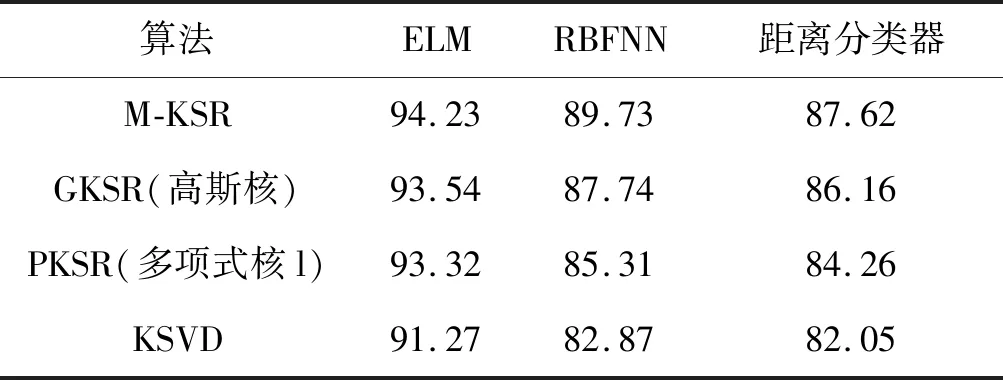
表2 不同算法下的特征分类结果(主分量个数为324)Tab.2 Feature classification results of the different algorithms (324 principal components) (%)

7 结 论

考虑多核函数在模式识别中的应用优势,采用多项式核函数、高斯核函数和Sigmoid核函数的线性组合形式构成多核函数,提出一种改进的基于多核函数的稀疏表示模型,并在PCA特征子空间内,把该模型应用于PolyU掌纹数据库的图像分类。在相同实验条件下,采用不同的分类器进行掌纹特征分类测试,仿真结果表明,多核稀疏表示模型的掌纹特征分类效果明显优于单核稀疏表示模型和典型的KSVD稀疏表示模型,特别是在ELM分类器下,采用较少特征即可得到较高的分类精度。由于构成多核函数的核函数模型以及个数对特征分类结果影响较大,因此如何选择最优的多核函数将是进一步的研究方向。