单目机器人手眼标定研究*

邓仕超，梅 枫，高兴宇，杨 龙，梁晨光

(桂林电子科技大学a.机电工程学院;b.广西制造系统与先进制造技术重点实验室，广西 桂林 541004)

0 引言

机械手的手眼标定基本任务是计算机器手末端抓手坐标系与视觉传感器坐标系之间的相对齐次变换矩阵，实现通过视觉传感器识别目标并计算出目标在机械手基坐标系下的三维坐标，最终实现机械手对目标的抓取、焊接等操作。本文利用视觉传感器与机器手相结合，估计机器手末端工具坐标系到视觉传感器坐标系的转换矩阵。视觉传感器主要是由相机构成，通过相机来确定被测物的二维坐标，实现对物体坐标的测量。机械手手眼标定通常使用的“AX=XB”模型是Koide K等[1]在1989年首次提出的。在过去的30年里，出现了大量求解手眼标定方程AX=XB的方法。一般来说求解方法可以分为两大类：①分步法，先求解旋转矩阵，再求解平移矩阵。如Wu J等[2]提出的基于四元数的求解手眼标定转换矩阵方法；Daniilidis K[3]提出的对偶四元数方法；Andreff N等[4]提出的基于希尔维斯特方程的求解方法。②同步法，同时求解旋转和平移矩阵。如Gwak S等[5]提出的梯度/牛顿法；Wu J等[6]提出的线性矩阵不等式法。

每种算法都有不同的优点和缺点，分步法在平移矩阵的精度比旋转矩阵的精度高时，会把旋转矩阵的误差代入平移矩阵中，影响整体的手眼标定精度。同步法可以得到很好的结果，但在数据迭代上会花费大量的时间。同时不同的数学方法来求解手眼标定方程过程中，由于机器正运动学建模、线结构光视觉传感器标定等引入误差，使得求解机械手末端坐标系到视觉传感器坐标系的转换矩阵较为复杂。为使手眼标定的复杂度降低，本文基于四元数法提出了一种单位八元数方法来估计视觉传感器到机械手的转换矩阵，通过实验使用该方法使得手眼标定的求解过程相对简单，计算效率提高。

1 手眼标定矩阵方程式的求解

单目机械手手眼标定模型如图1所示，为了方便手眼标定，现建立如下坐标系:机械手基坐标和世界坐标系重合Ow-xwywzw，机械手末端坐标系Oe-xeyeze，摄像头坐标系Oc-xcyczc，标定板坐标系OG-xgygzg，手眼标定方程式AX=XB化为齐次矩阵[7]为：

(1)

式中，Ra、Rb分别为机械手末端和相机坐标系的3×3旋转矩阵；Ta、Tb分别为对应的3×1平移矩阵；Rx、Ta是代求解的机械手末端和相机坐标系的旋转矩阵和平移矩阵。解耦得到旋转公式、平移公式分别为：

Ra×RX=RX×Rb

(2)

Ra×TX+Ta=Rb×Tb+TX

(3)

图1 手眼标定结构简图

1.1 基于3-D旋转的最优估计

使用ai、bi来表示机械手和相机在仅做旋转运动时的一组转换矩阵，由旋转公式(2)，可得：

(4)

其中，

ai=[log(Rai)]^

(5)

bi=[log(Rbi)]^

(6)

通过对式(4)使用SVD(Singular Value Decomposittion)来求解可以得到旋转矩阵RX，再把RX反代入式(3)可以得到平移矩阵TX，但使用分步求解的方法，会把旋转矩阵的误差代入到平移矩阵中[8]。因此，也可以使用迭代的方法，同时得到TX、RX。

(7)

但式(6)也不能达到局部最优解[9]。我们使用一种新的视角去对手眼标定方程AX=XB进行4-D分析。

1.2 基于4-D旋转优化估计

旋转矩阵R可以使用两个四元数qL=(a,b,c,d)T,qR=(p,q,r,s)T来表示[10]。R、qL、qR的关系可以表示为：

R=RL(qL)×RR(qR)

(8)

式中，RL、RR使用四元数乘积来表示：

(9)

(10)

旋转矩阵R通过式(8)进行参数,σ由单位八元数统一表示，通过求解其的封闭解来求出旋转矩阵R和平移矩阵T。

(11)

由式子(11)的旋转矩阵R可以表示为：

R=(c1,c2,c3,c4)

(12)

对矩阵R进行列c1,c2,c3,c4建立相似的因式分解，则有：

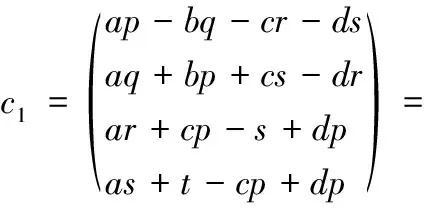
(13)

根据式(11)、式(13)可以得到P1(σ),P2(σ),P3(σ),P4(σ)是4×8的矩阵，并满足：

(14)

同理R也可以被分解为行并进行因式分解

R=(σTQ1(σ)σTQ2(σ)σTQ3(σ)σTQ4(σ))T。

(15)

为了解决式(7)不能达到局部最优解，把手眼标定模型AX=XB从SO(3)转到SO(4)上，进行对手眼标定方程的求解。由于AX=XB在SO(4)的求解与之前用于求解旋转四元数分解的四元数旋转分解QDR (quaternion decomposition from rotation ) 非常相似，所以可以在QDR的基础上对旋转八元数分解。

1.3 手眼标定方程求解

设Ei、Zi为机械手和摄像机视觉传感器的坐标系在4-D下转换矩阵，由式(2)，可得：

(16)

式中，Ei∈SO(4),Zi∈SO(4)其指数映射为6×6的斜对称矩阵。

文中定义Ei、Zi如下所示：

Ei=(ei,1,ei,2,ei,3,ei,4)
Zi=(zi,1,zi,2,zi,3,zi,4)

(17)

将式(17)代入EiRx-RxZi，由矩阵的性质可得：

(18)

由式(18)可以得到EiRx-RxZi=(Mi,1σ,Mi,2σ,Mi,3σ,Mi,4σ)，则有：

(19)

式中，每一个Gjk,i,j,k=1,2,3,4如下：

(20)

其中，参数矩阵Jjk,i∈R4×8。由式(17) ～ 式(20)可以求解最优单位八元数。

(21)

式中，

(22)

式(21)中的σ是矩阵F的最小特征值对应的特征向量，特征值与特征向量的关系有：

Fσ=λF,minσ

(23)

(24)

(25)

(26)

假设经过测量得到Ei、Zi，构建手眼标定模型，由式(22)得到特征向量qL和qR，代入到式(8)进而可以确定机械手末端与视觉传感器坐标系之间的转换矩阵R。

1.4 手眼标定方程SO(4)参数化

确定了手眼标定模型AX=XB在SO(4)下的求解方法，下面在来考虑得到的坐标系的转换矩阵如何从SO(3)转到SO(4)的求解。Thomas F[11]提出了矩阵从SO(3)到SO(4)的转换关系为：

(27)

式中，ε满足ε2=0，为了满足等式，实际我们设ε=1/d，当d>>1时，可以满足等式，经过实际的实验[12]我们取d=1×107。

2 实验与结果

根据以上算法展开实验，通过如图2所示的机器手进行手眼标定实验，六自由度机械手的重复定位精度优于0.04 mm，相机的分辨率为2592～1944 ppi，相机工作时的焦距为12 mm，按上述方法进行手眼标定实验，实验的步骤为：

(1)通过移动机械手获取N组机械手末端和视觉传感器坐标系的坐标，六自由度机械手的重复定位精度优于0.04 mm，为了保证稳定性和实验准确度，应使N>3。

(2)将得到Ai、Bi代入式(27)，将数据从SO(3)转到SO(4)上。

(3)通过式(16)～式(26)对AX=XB方程进行求解，并将计算得到R通过式(27)转到SO(3)上。

(4)把计算得到R进行实际的应用，计算精度。手眼标定实验采用11×8棋盘格作为相机标定和手眼标定的固定靶标。在实验过程中，先对摄像头使用棋盘格标定，内参和畸变系数如表1所示，再进行手眼标定实验，通过标定板固定不动，机器手移动，分别记录相机、机械手在不同位置下的外参和基坐标到机械手末端的末端坐标，为简要描述手眼标定的过程，本文摘取6个机器手位姿和相机外参数据如表2所示。

图2 AX=XB手眼标定实验场景

表1 相机内参系数和畸变系数

表2 手眼标定数据

从表2可知，任区2组可构成一个手眼标定方程，通过本文算法得到手眼关系矩阵为：

为了验证手眼关系矩阵的可靠性，重复进行10组完全独立的实验，通过机械手末端坐标，手眼转换矩阵，相机位姿公式计算得到该点在机械手基坐标下的坐标，通过与真实值进行比较，其结果的三维坐标对比，如图3～图5所示。

图3 X轴坐标比较

图4 Y轴坐标比较

图5 Z轴坐标比较

从图中观察根据手眼关系转换矩阵计算的结果与实际点的X、Y的坐标误差在视觉传感器对的工作范围内可以达到0.5 mm以内，基本满足要求，而Z轴的误差较大的原因是为了避免机器手碰到实验台，在测量实际值时引入一定的误差导致的。误差主要是由于实际点坐标在使用机器手测量时不能百分百的保证对准测量点的人为误差，该误差不可以避免但可以尽可能减少。另一方面，相机标定的内参、畸变系数、外参求解和手眼标定模型的求解，在计算过程中会产生误差，这对测量点的坐标产生误差，但标定产生的误差非常小，这样的计算误差是可以接受的。综合上述实验分析，本文的算法具有精度高、鲁棒性好的能力。

3 结论

本文构建以一种基于单目机械手手眼关系标定的测量系统，利用棋盘靶标作为参考物，使用单位八元数方法来求解手眼标定模型AX=XB，来确定相机和机械手末端之间相对姿态的转换方法。本算法最大限度避免了旋转矩阵误差代入到平移矩阵中，该算法比手眼标定传统四元数算法的速度快，且鲁棒性好。最后通过测量棋盘格板定板进行精度验证，实验结果表明系统具有良好的识别能力、较高精度和稳定性，满足实际的应用要求。但单相机对检测物体三维空间坐标的精度不高，需要配合更多的传感器，后续将继续开展相关工作。