混凝土倒锥壳水箱三种内力计算方法对比研究
2021-12-29韩俊良郁有升王卫国谢义德
韩俊良,郁有升,王卫国,谢义德
(1.青岛市建筑设计研究院集团股份有限公司,青岛 266033;2.青岛理工大学 土木工程学院,青岛 266525;3.山东省高等学校蓝色经济区工程建设与安全协同创新中心,青岛 266525;4.青岛安装建设股份有限公司,青岛 266033;5.青岛市政空间开发集团有限责任公司,青岛266000)
水塔作为一种储水供水的特种结构,目前在国内应用较少,但是在非洲国家的工业及民用供水工程中应用较为普遍,其中钢筋混凝土倒锥壳水塔结构具有合理、施工方便、造型美观等优点使其成为大容量水塔设计的首选。
熊学文[1]结合实际工程,介绍了大容积倒锥壳水塔的设计及施工安装等内容,为同类工程提供了参考。徐波[2]以500 m3倒锥壳水塔为例,对其结构计算分析和设计过程做了详细介绍。潘东岳[3]结合1000 m3倒锥壳水塔的设计工程,重点阐述了大容积倒锥壳水箱的设计方法及设计中应注意的问题。为了改善倒锥壳水箱预制提升后漏水严重的问题,许多学者对倒锥壳水箱高空现浇技术进行了研究[4],并取得了大量成果,提高了工程质量和施工安全性。倒锥壳水塔在地震作用下的受力性能复杂,蓄水量对水塔的抗震性能有较大影响[5]。国内外学者对水塔的抗震性能进行了研究,GURKALO等[6]通过在支筒上设置带轴支撑的竖向夹缝,来降低支筒底部的应力集中以及提高水塔的抗震性能。GHATEH等[7]通过有限元软件研究了高水位水塔的地震响应修正系数,为水塔的抗震设计提供参了考。倒锥壳水箱的内力计算是水塔设计的重要环节,计算过程比较复杂,通常采用有弯矩理论和无弯矩理论两种方法[8-9]。俞锋等[10]采用无弯矩理论和有弯矩理论,分别计算了300和500 m3倒锥壳水箱的内力,有弯矩理论的计算结果更为精确。何迅[11]通过对50和300 m3倒锥壳水塔水箱按有弯矩理论和无弯矩理论进行了对比,结果表明300 m3倒锥壳水箱边缘处干扰力的影响不可忽视。已有的研究主要针对小容积的倒锥壳水箱,但是随着经济的发展,大容积水塔的需求量不断增加,对大容积倒锥壳水塔设计方法的研究相对较少。
SAP2000有限元软件为倒锥壳水塔的设计提供了一种方便快捷的计算手段。目前针对SAP2000应用于大容积倒锥壳水塔的研究较少,对于SAP2000计算结果与两种理论计算结果的对比还有待进一步研究。本文分别采用了有弯矩理论、无弯矩理论和SAP2000软件对水箱(容积1200 m3)进行了内力计算。通过对3种计算方法所得结果的比较,得出适合大容积水箱的设计方法,旨在为倒锥壳水塔的精确设计提供参考依据。
1 倒锥壳水箱设计
安哥拉水塔工程所采用的水箱为不保温水箱,由环梁、倒锥壳和正锥壳三部分组成。贮水部分为倒锥壳,顶盖部分为正锥壳,混凝土采用C30。水箱的容水量为1200 m3,本工程采用了有弯矩理论和无弯矩理论对水箱进行了内力分析。水箱的轴线尺寸如图1所示。
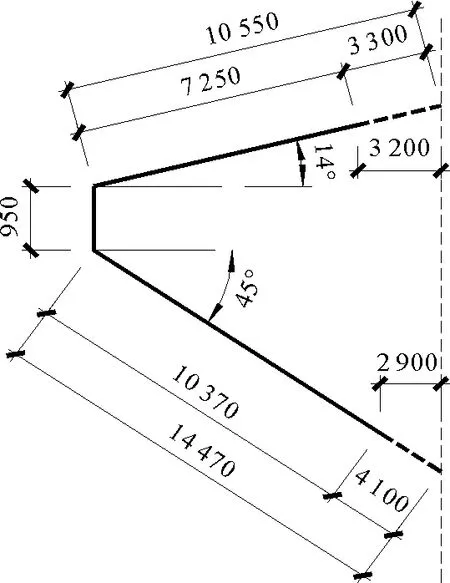
图1 水箱轴线尺寸(单位:mm)
1.1 荷载计算
水箱内力分析时考虑的荷载包括自重、水荷载、活载。荷载计算简图如图2所示,荷载取值见表1。其中,P1为上环梁自重及气楼传来的荷载,P2为中环梁自重;q1为上壳自重及活荷载,q2为下壳自重,q3为平均水压,q4为三角形水压。

图2 水箱荷载

表1 水箱荷载
1.2 倒锥壳水箱计算理论
无弯矩理论(薄膜理论),计算时只考虑壳体结构的径向力及环向力,不考虑壳体内部及边缘处弯矩的影响,由静力平衡方程计算出锥壳的轴向力。下面以下锥壳自重为例,介绍下锥壳的内力计算简图及计算公式[12]。计算简图如图3所示。

图3 下锥壳薄膜内力计算简图
径向力:
(1)
环向力:
Nθ=-q0tcosφcotφ
(2)


图4 壳体变形及各部位几何关系

ΔH=ΔH0+ΔHm+ΔHh
(3)
ψ=ψ0+ψm+ψh
(4)
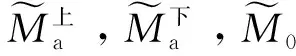
(5)
(6)
(7)
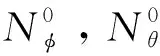
(8)
(9)
(10)
(11)
1.3 倒锥壳水箱内力计算
用无弯矩理论和有弯矩理论对容量为1200 m3的水箱进行内力计算,其中Nφ,Nθ,M为壳体上任意一点单位长度的径向力、环向力和弯矩值。计算时壳体按照0.5 m的距离进行等分取点,水箱各点内力计算结果如表2所示,内力分布如图5所示。

表2 水箱内力计算结果
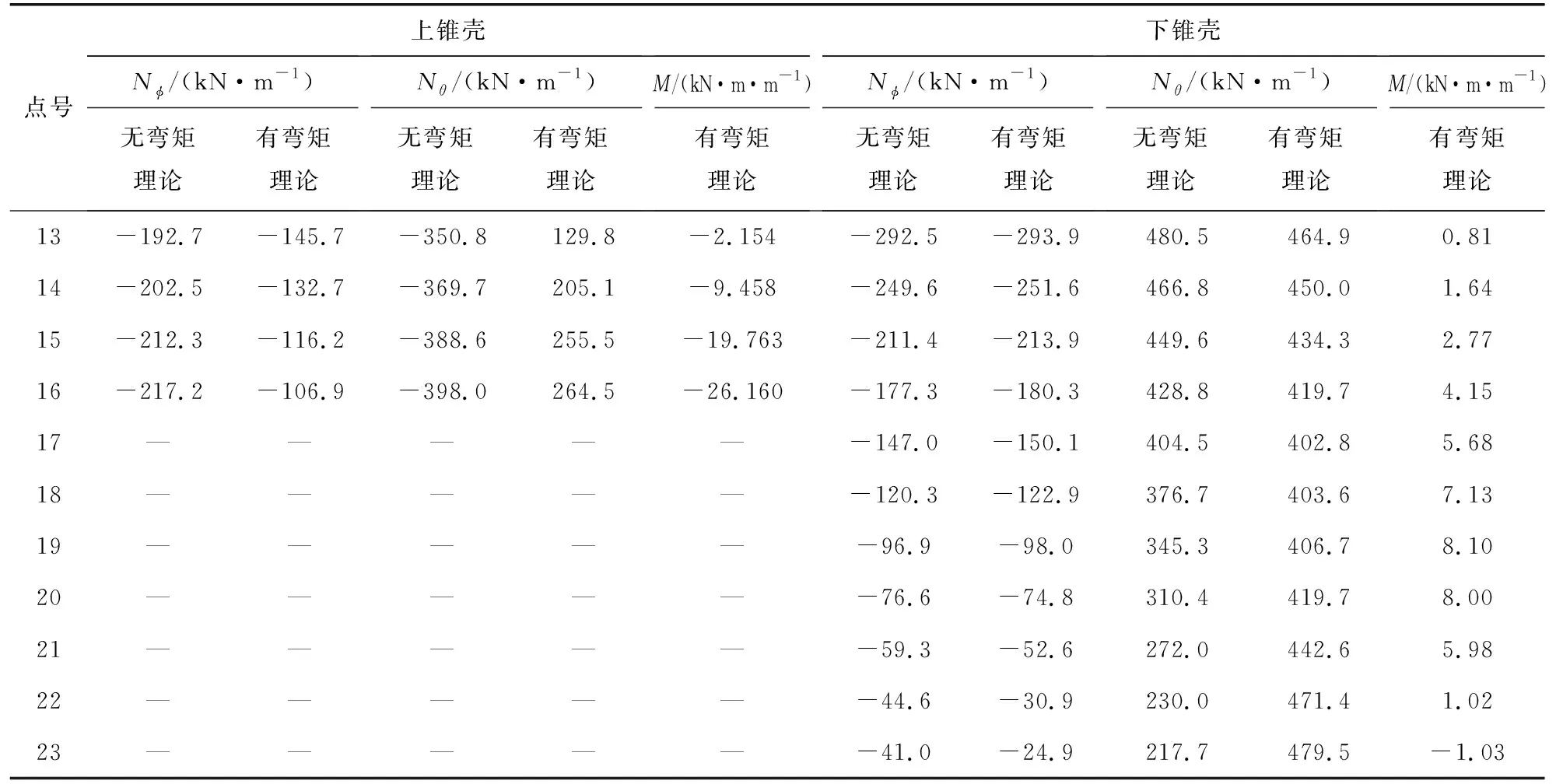
续表2
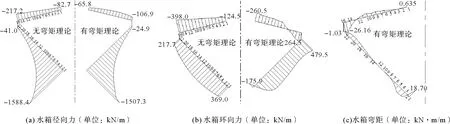
图5 水箱内力分布
由图5可知,无弯矩理论和有弯矩理论的计算结果差别比较明显,特别是对环向力的影响更为显著。上壳与中环梁连接处,由无弯矩理论计算的是压力,但是有弯矩理论,考虑了边缘效应和协调变形得出的结果是拉力。下壳与下环梁连接处无弯矩理论计算的为拉力,有弯矩理论计算的为压力。径向力计算结果表明:有弯矩理论与无弯矩理论的计算结果相比,上壳内环处径向力减小了20.4%,上壳外环处径向力减小了50.8%。下壳内环处径向力减小了5.1%,下壳外环处径向力减小了39.3%。壳体中部内力几乎没有变化。计算理论的不同,对上壳内力计算结果的影响大于下壳,对外环的影响大于内环,对壳体端部的影响大于中部。对环向力的影响大于径向力。
2 有限元模拟及对比分析
采用SAP2000有限元软件对水箱进行内力计算,通过有限元计算,得出水箱内力云图和水箱内力的分布规律。采用SAP2000壳单元对水箱进行了整体建模,倒锥壳水箱位于支筒顶部,支筒底部固节。考虑环梁对壳体的约束作用,环梁采用梁单元建模,水箱采用壳单元建模。水箱环向划分成18份,下壳沿径向划分为24份。根据水箱的实际受力情况对水箱上壳施加活荷载3 kN/m2,下壳施加水压力。自重由软件自动计算。从软件中分别输出结构的径向力和环向力,结果如图6—10所示。分别将上壳(下壳)内环和外环处的有限元计算结果与理论计算结果进行比较,结果如表3所示。
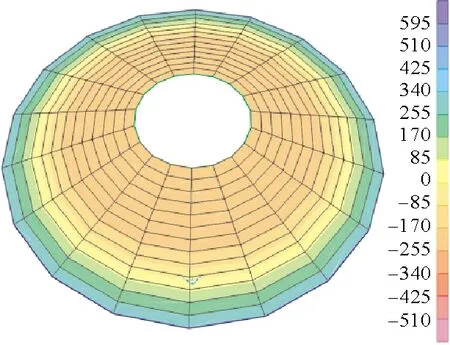
图6 上壳环向力
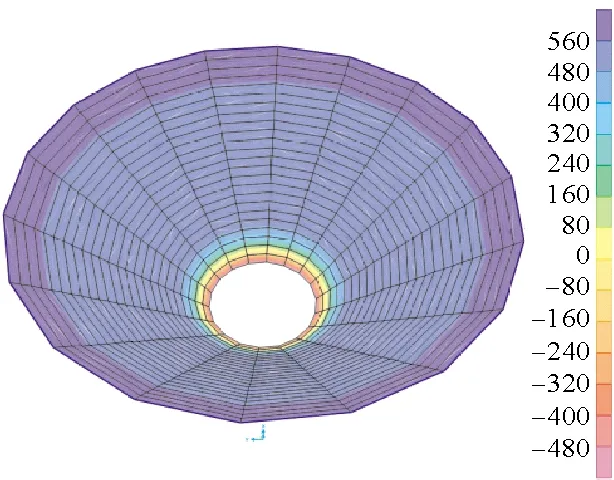
图7 下壳环向力

图8 上壳径向力

图9 下壳径向力

表3 有限元结果与理论计算结果对比
从表3可以看出有弯矩理论计算结果与SAP2000的计算结果比较接近。在下壳内环梁处,与SAP2000计算结果相比,径向力有弯矩理论结果误差最小为4.2%,环向力误差为2.22%,相应的无弯矩理论误差为0.95%和254%。从有限元云图及水箱内力图可以看出,下环梁附近径向力较大,且衰减较快,因此在设计时此处应做加腋处理,以提高水箱的抗裂性能。下壳外环梁处两种计算理论得到的结果与有限元结果都有较大的差别,其中有弯矩理论的径向力比有限元结果小了35.1 kN,环向力小了124.5 kN。主要原因为:理论计算时,对中环梁与壳体连接处的边界假定为弹性固定,中环梁的截面较大,在计算时考虑的环梁对壳体的约束作用较强,造成计算结果偏小;同时,有限元计算时,环梁与壳体连接处不能平缓过度,SAP2000中的壳单元与梁单元的连接以及协同工作与实际情况存在偏差,软件中所建模型不能准确地模拟中环梁对壳体的约束作用,以上原因导致中环梁处理论计算结果与有限元模拟结果存在较大误差。设计时建议采用加腋和增加配筋等方式适当增强下壳与中环梁的连接。有弯矩理论计算的上壳内力与有限元结果十分接近。最大误差为5.84%,最小误差为0.19%,均满足工程设计要求。总体来看,有弯矩理论的计算结果与结构的实际受力情况比较接近。由图10和图5对比可以看出,有弯矩理论和SAP2000计算而得的壳体内力曲线的变化规律相同。虽然无弯矩理论计算结果与有弯矩理论和有限元结果相比误差较大,但是其计算过程简单,效率高,不容易出错。在初期方案设计阶段,由于水箱尺寸、壁厚等各项参数未确定,可采用无弯矩理论进行初步计算,计算结果可满足初步设计要求。
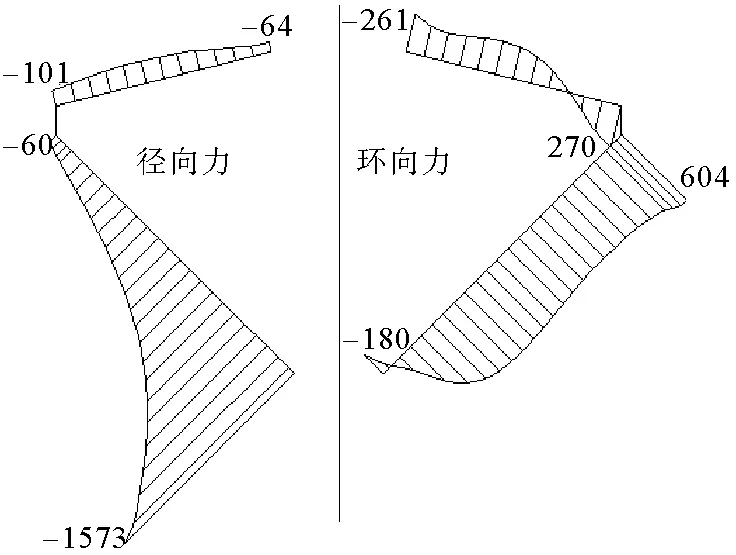
图10 有限元得水箱内力
3 结论
结合实际工程,介绍了倒锥壳水塔的设计过程,结论可为同类工程设计提供理论依据。并且选择了3种不同的计算方法对水箱进行了内力计算,通过对计算结果的对比分析得出以下结论:
1) 计算理论不同会对水箱内力的计算结果产生影响,影响规律主要表现为:计算理论不同对环向力的影响大于径向力,对上壳内力的影响大于下壳,对外环处内力的影响大于内环,对壳体端部内力的影响大于中部。
2) SAP2000计算结果与有弯矩理论计算结果比较接近,内力曲线变化规律相同,证明了有弯矩理论的计算结果更加符合水箱的实际受力情况。
3) 在上、下壳内环处有弯矩理论与SAP2000结果比较接近,误差在0.19%~4.2%;上、下壳外环处误差稍大,且下壳外环处的误差最大。
4) 无弯矩理论计算结果误差大,但计算简单。有弯矩理论计算结果精确,但计算过程复杂,参数较多容易出错。因此在水塔初步设计时,可以采用无弯矩理论,精确设计时应选择有弯矩理论和有限元结合进行计算,以保证计算结果的准确性。
