分布式多无人机编队控制与博弈算法研究*
2021-12-29马特郑致远赵军虎
马特,郑致远,赵军虎
(火箭军工程大学,陕西 西安 710025)
0 引言
多无人机(unmanned aerial vehicles,UAVs)系统的编队队形控制问题多年来一直是研究热点[1-3]。对于多无人机编队问题,分布式控制方法相较于集中式的控制有很大的优势[4],主要体现在:①实现“去中心化”,每个智能体和邻居智能体进行单向或者双向通信,不需要一个中心智能体,因此,节约了通信成本。②每个智能体都能进行独立计算并决策,具有良好的自主性,同时保护了个体隐私。③系统具有良好的拓展性和鲁棒性。在军事斗争中,甚至单个智能体遭到破坏,其他智能体仍然能够照常完成目标任务。④单个智能体都可以独立控制自身行为,因而系统具有很好的适应性。近年来,为了实现多智能体的自主编队,不少学者提出了分布式控制算法。例如,文献[5]研究了只需要测量相对位置实现多智能体编队的分布式控制算法;文献[6]研究了有限时间多智能体系统的一致性分布式控制算法;文献[7]利用相对位置反馈实现缩放尺寸的分布式编队控制算法;文献[8]研究了多机器人的分布式自适应一致性追踪控制算法。以上研究都针对编队问题展开,实际上,多无人机的编队可以转化为分布式博弈问题来解决。
近年来,由于其在金融[9]、环境工程[10]、能源领域[11]以及军事斗争领域[12]的广泛应用,博弈问题即纳什均衡点(Nash equilibrium)的求解问题得到了广泛关注。很多学者在博弈问题的理论研究和工程实践应用都做出了相关的研究。例如,文献[13]研究了博弈论在投标决策过程中的影响;文献[14]结合神经网络研究了博弈论在数字土壤映射中的应用。文献[15]基于博弈论研究了舰载无人机编队协同目标分配问题;文献[16]基于纳什议价研究了无人机自主编队自主重构控制方法。
目前,很少有人将多无人机的编队队形问题与博弈论相结合的研究。本文研究了多无人机的编队队形控制问题,将无人机的编队问题转化为博弈问题即纳什均衡点的求解问题,基于状态反馈控制和梯度下降,设计了分布式控制算法。在飞行编队中,每个无人机个体并不需要其他所有无人机的位置信息,只需要邻居无人机的信息,最终实现无人机的编队。
1 多无人机编队与分布式博弈
1.1 多无人机编队
考虑架四旋翼无人机系统的编队队形控制问题,其中无人机的动态系统可以表示为
(1)

无人机编队控制的目的是设计无人机的控制输入ui,实现多无人机的自主编队。
1.2 分布式博弈问题
在分布式博弈中,博弈个体之间存在博弈关系,每个博弈个体的目标不但和自己有关还和其他博弈个体相关,每个博弈个体都想通过改变自己的决策来达到自己的目的。
1.2.1 图论
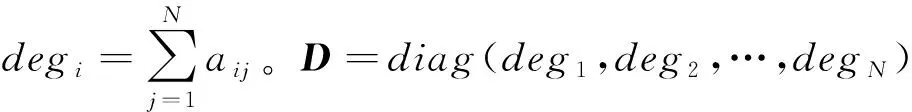
1.2.2 博弈问题描述
在博弈问题中,每一个博弈个体都有一个代价函数,这个代价函数不但和自己的行为决策有关,还和其他所有的博弈个体的行为决策有关。Ji(qi,q-i)∶RNm→R表示个体i的代价函数,其中qi∈Rm代表个体i的决策,q-i=col(q1,q2,…,qi-1,qi+1,…qN)代表其他博弈个体的决策,每一个博弈个体的目标都是最小化:
(2)
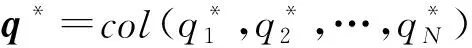
(3)
从式(3)可以得出,当博弈个体处于纳什平衡点的时候,任意一方个体都不能单独改变自己的决策来减小自己的代价函数,也就是说每个博弈个体都处于最差情况下的最优状态。
1.2.3 问题转化
多旋翼无人机系统(1)的编队使多无人机的位置达到理想值,而博弈问题的目标在于通过分布式算法使决策收敛到纳什均衡点。那么通过为无人机设计合理的目标函数使得纳什均衡点为无人机编队飞行的解。具体为无人机如下目标方程:
(4)

(5)
定理1.在无向连通图的通信拓扑下,q*=col(q1,q2,…,qN)是博弈问题(2)的纳什均衡点,当且仅当下列条件成立:
(6)

定理2.博弈问题(2)的解,即纳什均衡点满足多无人机理想编队要求,且编队的几何中心为
证.根据目标方程式(4)以及定理1,纳什均衡点满足
(7)
2 控制器设计
首先,旋翼无人机的动态模型可以被写成欧拉-拉格朗日系统的形式[19],即
(8)
式中:gi(qi)=[0,0,mig,0,0,0]T,τi=[Fi,Ni]T∈R6,Fi=R[0,0,ui]T,
(9)
R为由机体系转变到惯性系的转换矩阵,可以表达为

综上所述,无人机的动态模型转化为欧拉拉格朗日形式为
其中,Ez=[0,0,1]T。
基于状态反馈和梯度下降为多无人机系统设计如下分布式控制算法:
(10)
式中:k1,k2为控制增益;yij为辅助变量;y-i=col(yi1,yi2,…,yi(i-1),yi(i+1),…,yiN)。
定理3.旋翼无人机系统式(1)通过分布式控制算法式(10)可以实现博弈问题(2)的纳什均衡点的求解,即实现理想的编队。
证.首先,结合无人机系统式(1)和分布式控制算法式(10),得到:
(11)
写成紧凑的形式如下:
(12)

当系统达到平衡点的时候,得到:
(13)
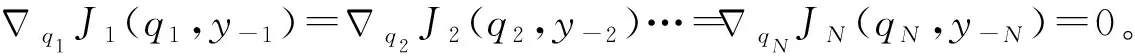
3 仿真校验
考虑6架旋翼无人机理想编队问题。通信拓扑选择环形图1所示。

图1 通信拓扑图Fig.1 Communication topology
即它的拉普拉斯矩阵为

(14)
6架无人机的系统参数如表1所示。
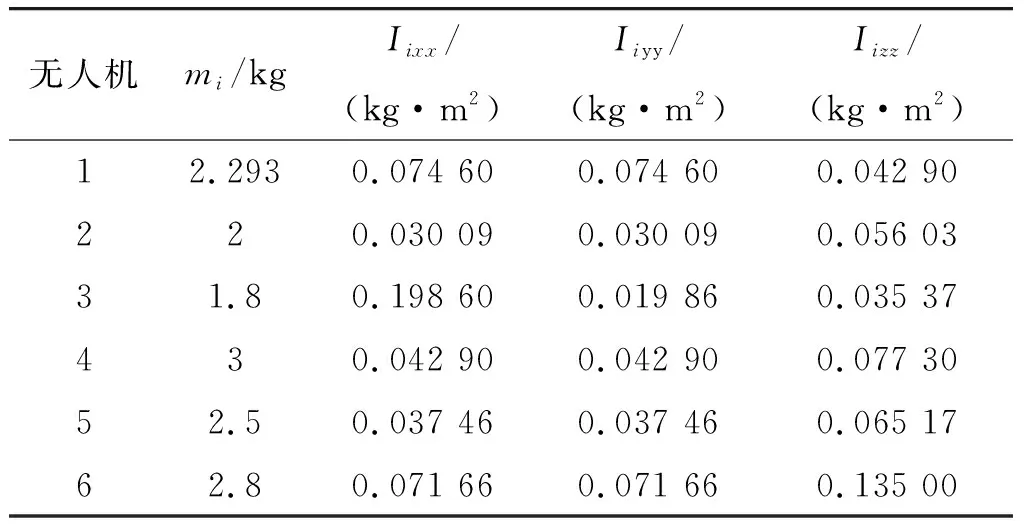
表1 旋翼无人机系统参数Table 1 Parameters of the six quadrotor UAVs
6架无人机的初始位置和初始欧拉角如表2所示。
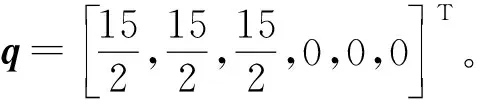
Δ1=[-2.5,-2.5,-2.5,0,0,0]T,
Δ2=[-2.5,2.5,-2.5,0,0,0]T,
Δ3=[-2.5,2.5,2.5,0,0,0]T,Δ4=[-2.5,-2.5,2.5,0,0,0]T,
Δ5=[22.5,0,0,0,0,0]T,
Δ6=[10,0,0,0,0,0]T.

表2 无人机的初始位置和初始欧拉角Table 2 Initial positions and attitudes
理想的编队模型如图2所示。

图2 理想编队模型Fig.2 Desired formation
如图3所示为6架无人机由初始位置运动到编队位置的轨迹。图4~6分别为无人机的滚动、偏航、俯仰角。仿真结果显示无人机姿态角幅值变化均未超出一般旋翼无人机的姿态角的约束要求。6架旋翼无人机从初始位置出发,通过改变姿态角运动至理想编队位置,而后姿态角恢复为0并保持此平衡状态。仿真结果充分验证了本文提出算法的有效性。

图3 旋翼无人机的编队飞行轨迹Fig.3 Position trajectories of UAVs

图4 无人机的滚转角Fig.4 Roll angles of UAVs
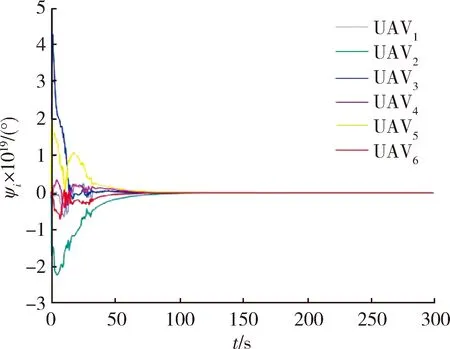
图5 无人机的偏航角Fig.5 Yaw angles of UAVs
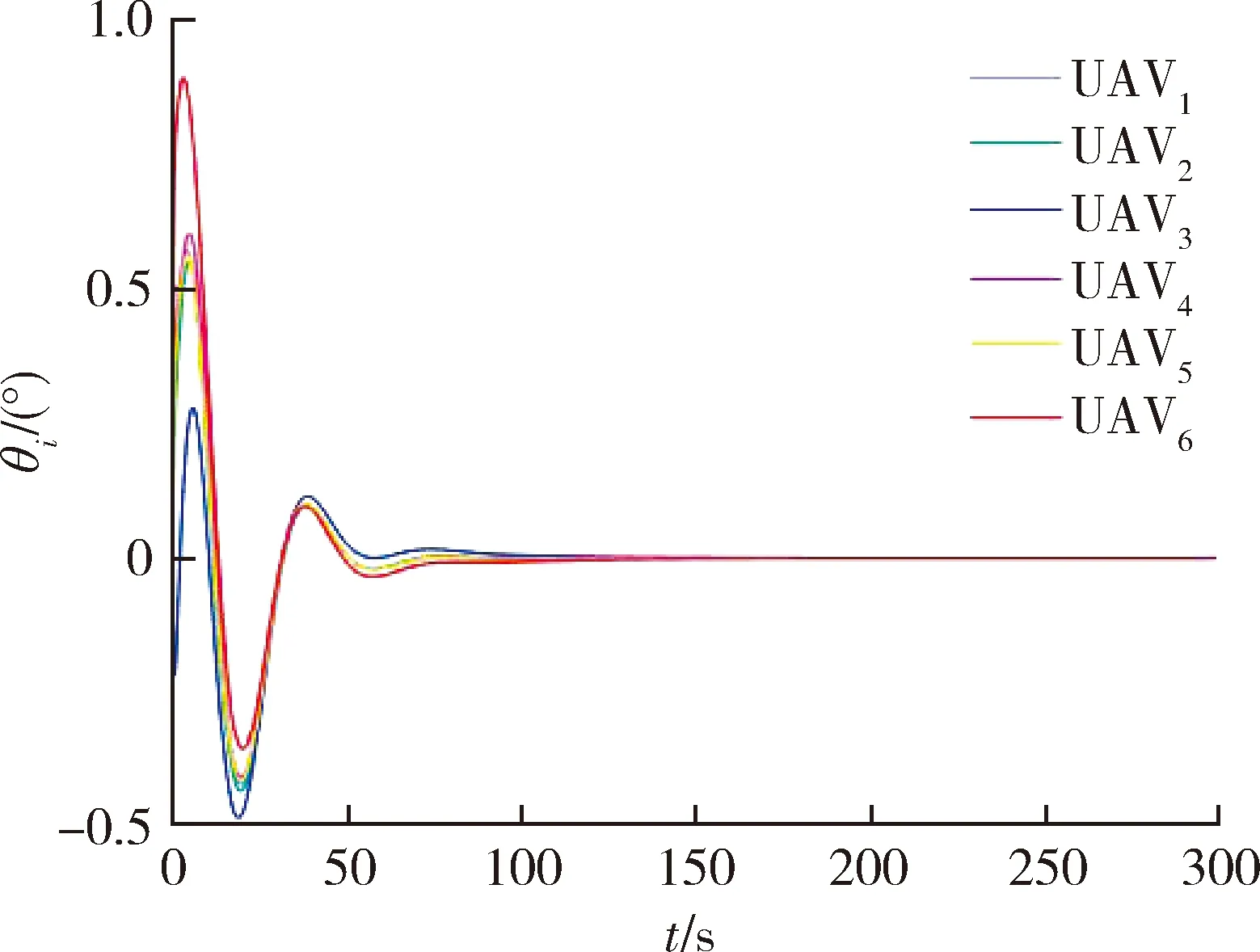
图6 旋翼无人机的俯仰角Fig.6 Pitch angles of UAVs
为了进一步验证算法的拓展性和鲁棒性,本文进一步考虑在编队过程中,任意通信中断情况下(无人机通信拓扑仍然满足无向连通的要求),无人机群完成理想编队的情况。
考虑原始无人机群理想编队问题,但在编队过程中时间t=25 s时,编号1,6的无人机之间的通信中断,在此状况下验证无人机群能否仍然完成理想编队任务。
仿真结果如图7所示,在时间t=25 s时,编号1,6的无人机之间的通信中断,虽然仿真实验中无人机的轨迹存在微弱抖动,但无人机群仍然较好完成了编队任务,证明了算法的鲁棒性。
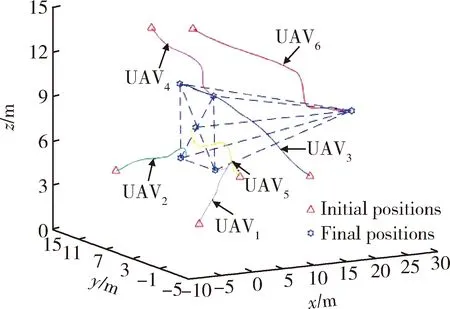
图7 部分通信中断下旋翼无人机的编队飞行轨迹Fig.7 Position trajectories of UAVs under communication interruption
4 结束语
针对多无人机的编队问题,本文将分布式控制与博弈论相结合,提出一种基于博弈的分布式控制算法。将多无人机的编队问题转化成博弈问题,利用一致性方法实现对多无人机的全局信息进行估计,通过梯度下降实现纳什均衡点的求解,最终实现理想编队。文中给出的仿真实例说明了该方法的有效性。
