基于鲁棒H∞控制的无人机纵向自动驾驶仪设计*

李勇，李树豪，党利

(郑州航空工业管理学院 航空工程学院，河南 郑州 450046)

0 引言

无人机(unmanned aerial vehicle，UAV)可以被定义为一种由动力驱动、机上无人驾驶的航空器[1]。固定翼无人机与旋翼无人机相比较，固定翼无人机的升力是由位于机身两侧的固定机翼所产生的，其优点是续航时间长、飞行速度快、飞行效率高和载荷大，缺点是起飞和降落时机场需要有长距离跑道以及不能进行空中悬停等[2]。

飞行控制技术是现代飞行器设计中的关键技术之一。在强劲的军事及民用需求牵引下，无人飞行器技术与飞行控制技术迅速融合，极大推动了无人机的蓬勃发展[3]。无人机已经在军事和民用中得到了广泛应用。军事应用包括侦察、监视(空中、陆地、海上)、边境巡逻和对地打击等。民用应用包括监视、森林防火、航拍及城市地图绘制等。

对无人机能力的日益增长的要求意味着有相当多的用来保证闭环系统稳定性、鲁棒性和性能的先进控制方法正在进行研究，如最优控制、鲁棒控制、非线性控制、智能控制等都是无人机飞行控制非常感兴趣的热点研究领域。

自20世纪50年代以来，根轨迹图、Bode和Nyquist图、频响分析等经典控制器设计技术在航空航天工业的自动飞行控制系统中得到了成功和广泛的应用。当要设计具有高内部耦合的多变量系统的控制器时，经典控制技术是有限的[4]。

在设计飞行控制器之前，必须确定飞机的数学非线性模型，传统上，模型参数是通过风洞试验测量飞机上的气动力和力矩来确定的。近年来，计算流体力学(computational fluid dynamics，CFD)方法变得越来越重要。在此基础上，计算了飞机的转动惯量，并根据实验数据确定了飞机发动机模型。然而，这些标准过程既昂贵又耗时，对于许多无人机应用来说可能负担不起或不可行[5]。

在实践中，大多数飞行控制设计技术都需要一个关于某些配平条件的飞机动力学的线性化模型。飞机线性模型通常由六自由度(six degree-of-freedom，6-DOF)非线性模型[6-8]导出，或者利用参数识别方法通过实验测量确定[9-11]。有了精确的线性模型，就可以成功地设计出飞行控制器。然而，线性模型永远不会是完全准确的。

由于真实的飞机动力学模型参数不是完全已知的，且飞机动力学是非线性的，所以飞机的飞行表示是不准确的。通常，这主要是因为有些特性不容易建模。此外，模型参数中存在未建模的动态和误差，因此在飞机动态模型中总是存在建模误差[12]。

近年来，国内在飞行器自动驾驶仪控制系统设计方面主要有以下成果及进展。文献[13]通过大量的数学仿真、地面半实物仿真和空中带飞试验，深入的考核了作者所在单位自主开发的无人机自动驾驶仪的整体设计性能，同时经过带飞试验进一步验证所采用的PID(proportional,integral and derivative)控制方法的可行性。文献[14]提出了一种新的实现无人机自动驾驶仪调参的方法。利用T-S模糊模型对被控对象进行建模,完成控制系统设计,然后利用模糊运算规则自动生成调参算法,明显提高了设计效率。无人机控制系统设计实例证明了方法的正确性。文献[15]在电传飞机纵向自动驾驶仪控制律的初步设计过程中,以电传飞机的纵向低阶等效系统为控制对象,采用零极点偶配置方法合理地配置零极点偶,使纵向自动驾驶仪控制律的设计得到了最大程度的简化。用所获得的控制律进行了数字仿真,仿真结果表明,纵向自动驾驶仪各个功能模式获得了良好的动态响应特性,满足了各项指标的要求,从而证明了这种设计方法是简便可行的。文献[16]提出了BTT(bank to turn)倾斜转弯导弹的增益调度鲁棒H∞自动驾驶仪设计方法，建立了BTT导弹线性变参数(linear parameter-varying，LPV)系统数学模型；提出了LPV系统增益调度鲁棒H∞控制设计方法和设计过程，通过把BTT导弹自动驾驶仪分为俯仰、偏航/滚转通道分别进行设计，并以俯仰通道为例进行了仿真验证；仿真结果表明该控制算法具有良好的控制性能，从而，验证了增益调度鲁棒H∞控制算法的正确性和有效性。

1 某固定翼无人机纵向LPV模型及纵向TP模型分析

本文提出了一种基于增益调度输出反馈H∞控制[17-19]的无人机纵向自动驾驶仪的设计方法，即速度保持和高度保持。需要采用线性变参数技术进行建模并用于整个飞行包线控制系统的分析和设计。

通常，LPV模型是使用代数处理方法从原始非线性方程模型导出的。然而，由这些方法得到的LPV模型往往是非线性依赖于时变参数的，尤其是纵向雅可比LPV模型，其非线性依赖于速度和高度。在非线性参数依赖的情况下，通常使用网格LPV模型来合成控制器，然而，启发式网格技术的结果是不可靠的，并且分析结果依赖于网格点的选择[20]。

本文采用TP(tensor-product)模型变换，将纵向非线性参数相关的LPV模型转换为TP凸多面体模型形式。

1.1 基于雅可比的纵向LPV模型

本文采用雅可比方法从标准六自由度运动方程出发，推导出适用于一般非线性模型且结构模型简单的纵向LPV模型。

考虑传统固定翼飞机的标准六自由度运动方程，虽然一般固定翼飞机的气动系数结构的确切形式并不确定，但文献[21-22]提出了典型的线性模型结构。本文中使用的文献[21]中的线性模型结构如下：

(1)

(2)

(3)

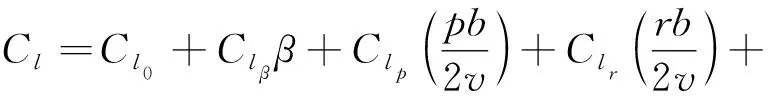
(4)

(5)

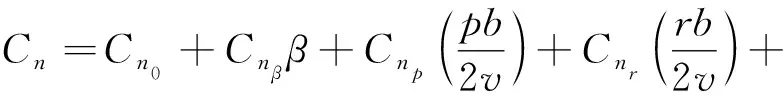
(6)

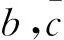
三维空间中的六自由度动力学方程，通常可以简化为二维空间中三自由度动力学的2个运动，即纵向运动和横向运动。在本文中，只考虑纵向运动。另外，假设飞机在机翼水平、高度和空速不变的情况下飞行，并且假设它只能在北方下部平面中机动，因此飞机所有侧向状态都冻结且等于0，即

v=p=r=β=φ=ψ=yE=0.

另外，当

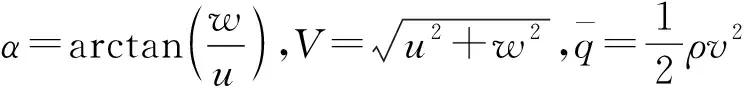
(7)

(8)

(9)

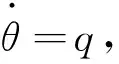
(10)

(11)

在工程实践应用中，无人机的质量惯性力矩Ix，Iy，Iz可以用文献[23]中提出的扭摆实验来确定，其中质量惯性力矩Ixz经常被忽略。此外，发动机推力T可以使用在文献[23]中提出的技术来建模和估计。本文中，推力是从表1中的数据建模的，在表1中，数据通过使用MATLAB软件TRIM函数来配平某型固定翼无人机非线性模型[24]在关于机翼水平、恒定高度和空速飞行条件下而获得的。

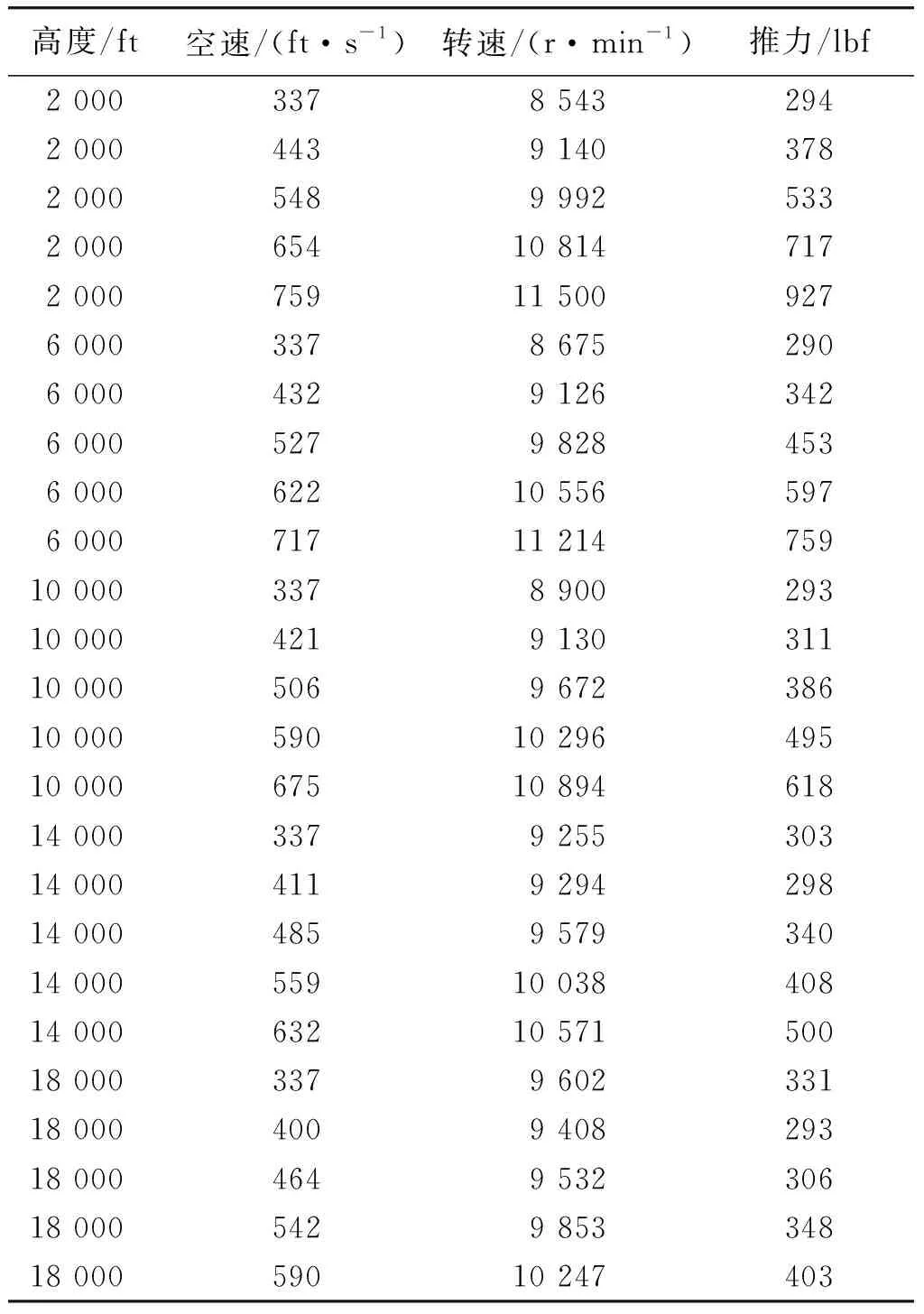
表1 关于某型无人机在机翼水平和恒定高度、 空速飞行状态下发动机仿真数据Table 1 Engine simulation data of a certain UAV at wing level,constant altitude and airspeed

推力的一个简单模型符合表1中的数据，它是

T=CT0+CTuu+CTuhuh+CTrpmrpm+

CTurpmurpm+CThrpmhrpm+

CTuhrpmuhrpm,

(12)

其中上述方程式中的所有推力系数在表2中给出。

表2 某型固定翼无人机的发动机推力系数Table 2 Engine thrust coefficient of a fixed-wing UAV

来自表1的模拟推力和来自式(12)的估计推力的比较如图1所示。

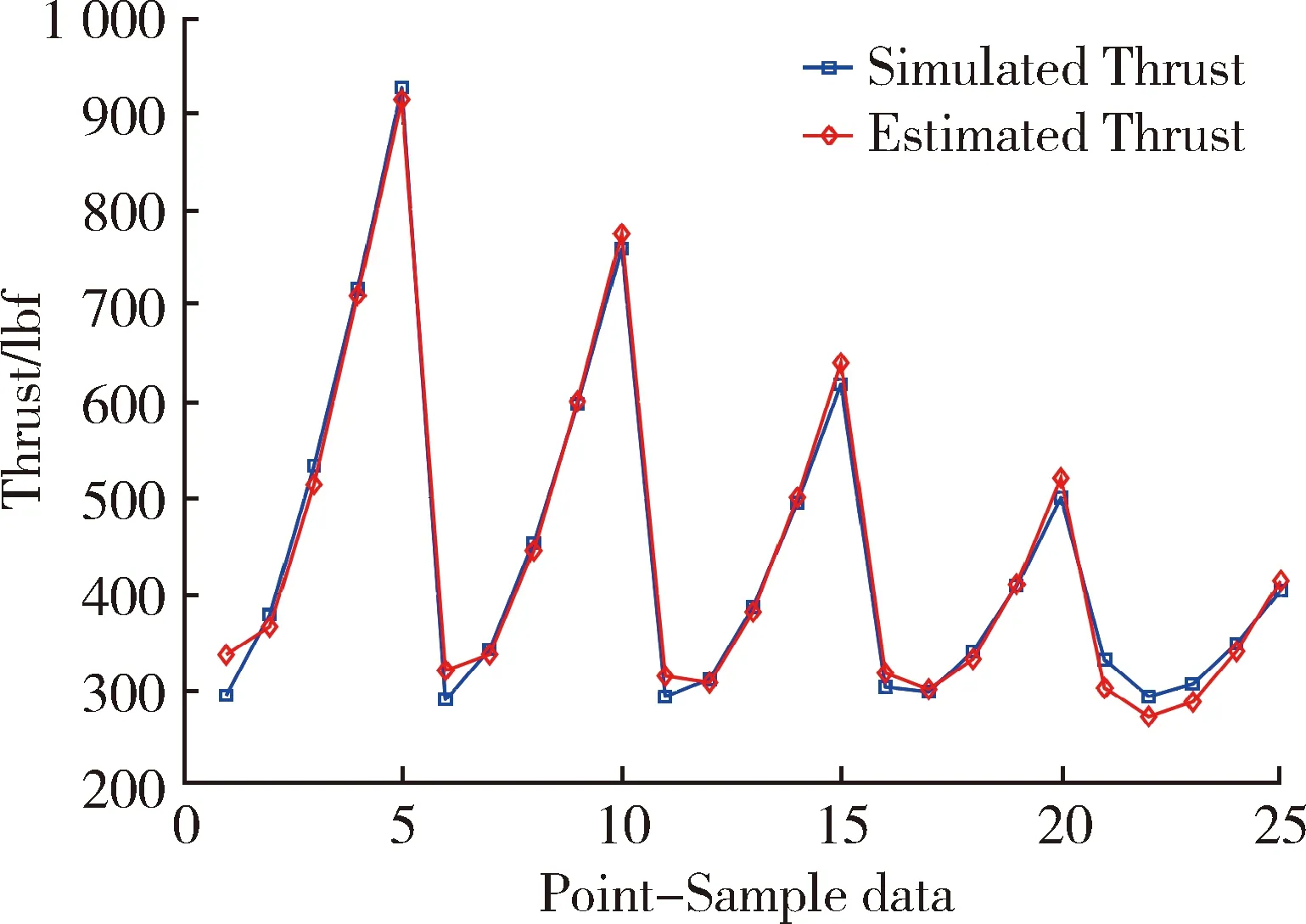
图1 模拟推力和估计推力之间的比较Fig.1 Comparison between simulated thrust and estimated thrust

针对某型固定翼无人机非线性数学模型。用雅可比线性化方法对该模型在机翼水平、恒定高度和空速飞行条件下线性化后，得到了作为状态空间系统的纵向LTI模型:

(13)

这里，

并且

CTurpmrpmtrim+CTuhrpmhtrimrpmtrim)，

(14)

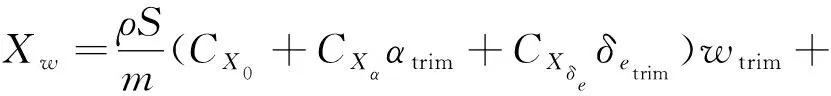
(15)

(16)

Xθ=-gcosθtrim，

(17)

(18)

CTuhrpmutrimhtrim)，

(19)

(20)

(21)

(22)

Zθ=-gsinθtrim,

(23)

(24)

(25)

(26)

(27)

(28)

hu=sinθtrim，

(29)

hw=-cosθtrim，

(30)

hθ=utrimcosθtrim+wtrimsinθtrim.

(31)

那么，可以得出

(32)

wtrim=utanαtrim,

(33)

θtrim=αtrim,

(34)

(35)

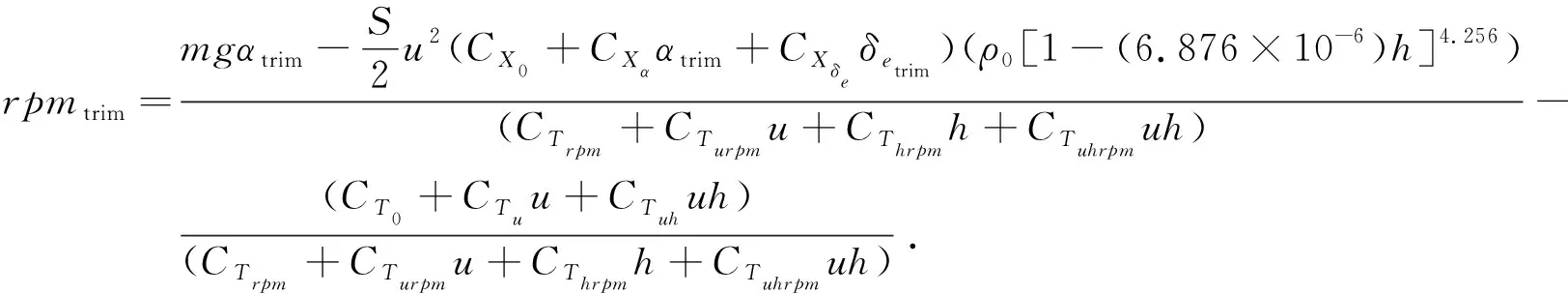
(36)

从式(14)～(36)可以看出，稳定性导数和控制导数仅与速度和高度呈非线性关系。在速度和高度一定的情况下，式(13)为纵向LTI模型。当速度和高度在整个飞行包线上缓慢变化时，式(13)成为一个纵向非线性参数相关的LPV模型。

此外，这些方程表明，该LPV模型的精度取决于提供气动力系数和推力系数信息的准确性。

传统上，空气动力系数通常是利用风洞试验通过测量引入到飞机上的气动力和力矩来确定的。在已知气动系数的情况下，纵向非线性参数相关LPV模型式(13)在整个参数空间的所有点的系统矩阵可以用式(14)～(36)确定。

1.2 纵向TP凸多面体模型

基于上节纵向非线性参数相关LPV模型(13)的系统，速度和高度是唯一的时变参数。某型固定翼无人机的整个飞行范围中，其速度和高度分别从337.6 ft/s到759.5 ft/s和1 000 ft到18 000 ft。

TP模型变换是一种可用于获得有限个LMI的替代方法，对于有限个LMI，该方法将给定的非线性参数相关的LPV模型(13)变换为TP凸多面体模型。应用MATLAB中的张量积模型转换工具箱来确定LTI顶层系统矩阵Sa和加权函数wa(p(t))。变换空间定义为Ω=[337.6，759.5]×[1 000，18 000]，采样网格密度为500×100。此外，在变换过程中使用了CNO凸包的加权类型，以便具有紧致的外壳表示。由此可得8×6×10×7的张量，其速度维度的奇异值分别为：39 198，2 554.5，697.63，49.012，1.048 6，0.032 623，0.000 503 45和4.248 3e-005。高度维度分别为：39 191，2 754.9，103.23，0.405 44，0.001 827 8和1.403 9e-005。

这意味着某型固定翼无人机的纵向非线性参数相关LPV模型可以精确地表示为8×6=48个LTI顶点系统的凸组合。然而，在实际应用中，控制器的数量较少，因此，只保留了速度和高度维度上的4个和3个最大奇异值，而在实际应用中，我们只保留了4个奇异值和3个最大奇异值。LTI顶点系统的个数减少到5×4=20。从理论上讲，L2矩阵范数逼近的最大误差是丢弃的小奇异值之和。

因此，

1.048 6+0.032 623+0.000 503 45+4.248 3e-005+0.405 44+0.001 827 8+1.403 9e-005=1.489 1。

将分解的TP多面体模型与原始的非线性参数相关的LPV模型式(13)在Ω给出的范围内随机选择2 000多个参数值(速度和高度)进行比较，得到L2矩阵范数的最大误差和平均误差分别为0.003 590 4和0.002 577 7。

分解的TP多面体模型可以将复杂度降低一半，同时它仍然可以足够精确地用于工程实际的实验。因此，纵向TP多面体模型可以写为

(Ai,jx(t)+Bi,ju(t))，

(37)

其中，权函数wn,j(pn(t))如图2所示。此外，图3显示了w1(p(t))和w2(p(t))作为确定wa(p(t))的一个示例。

图2 纵向TP多面体模型的一维参数的CNO型 凸权函数wn,j(pn(t))Fig.2 CNO type convex weight function of one-dimensional parameter of longitudinal TP polyhedron model,wn,j(pn(t))

图3 纵向TP多面体模型的二维参数的CNO型 凸权函数wa(p(t))Fig.3 CNO convex weight function of two-dimensional parameters of longitudinal TP polyhedron model,wa(p(t))

下面显示了该TP多面体模型的一些LTI系统矩阵Sa：

(38)

(39)

⋮

(40)

2 基于增益调度的H∞自动驾驶仪设计

在实际应用中，在应用鲁棒H∞控制方法设计一个LPV控制器之前，对象模型通常需要增加一些加权函数。在本文中，我们使用了混合灵敏度标准[25-26]。

(41)

该混合灵敏度函数的目的是分别用性能加权函数W1和鲁棒性加权函数W2对灵敏度函数S和控制灵敏度函数KS进行整形。由此，可得出一个善于跟踪指令(即跟踪误差较小)、善于抑制干扰(即减小干扰对输出的影响)、对测量噪声敏感性低、控制量较小、对附加对象扰动具有鲁棒稳定性的控制器。图4显示了用于合成的加权开环连接结构。

其中

(42)

(43)

(44)

Wpre-filter的目的是使被控对象模型的矩阵B2和D12与参数无关[17]，因此可以采用增益调度输出反馈H∞控制器设计方法[17]。此外，手动调整加权函数W1和W2的值，直到达到闭环系统的性能和鲁棒性的期望目标。

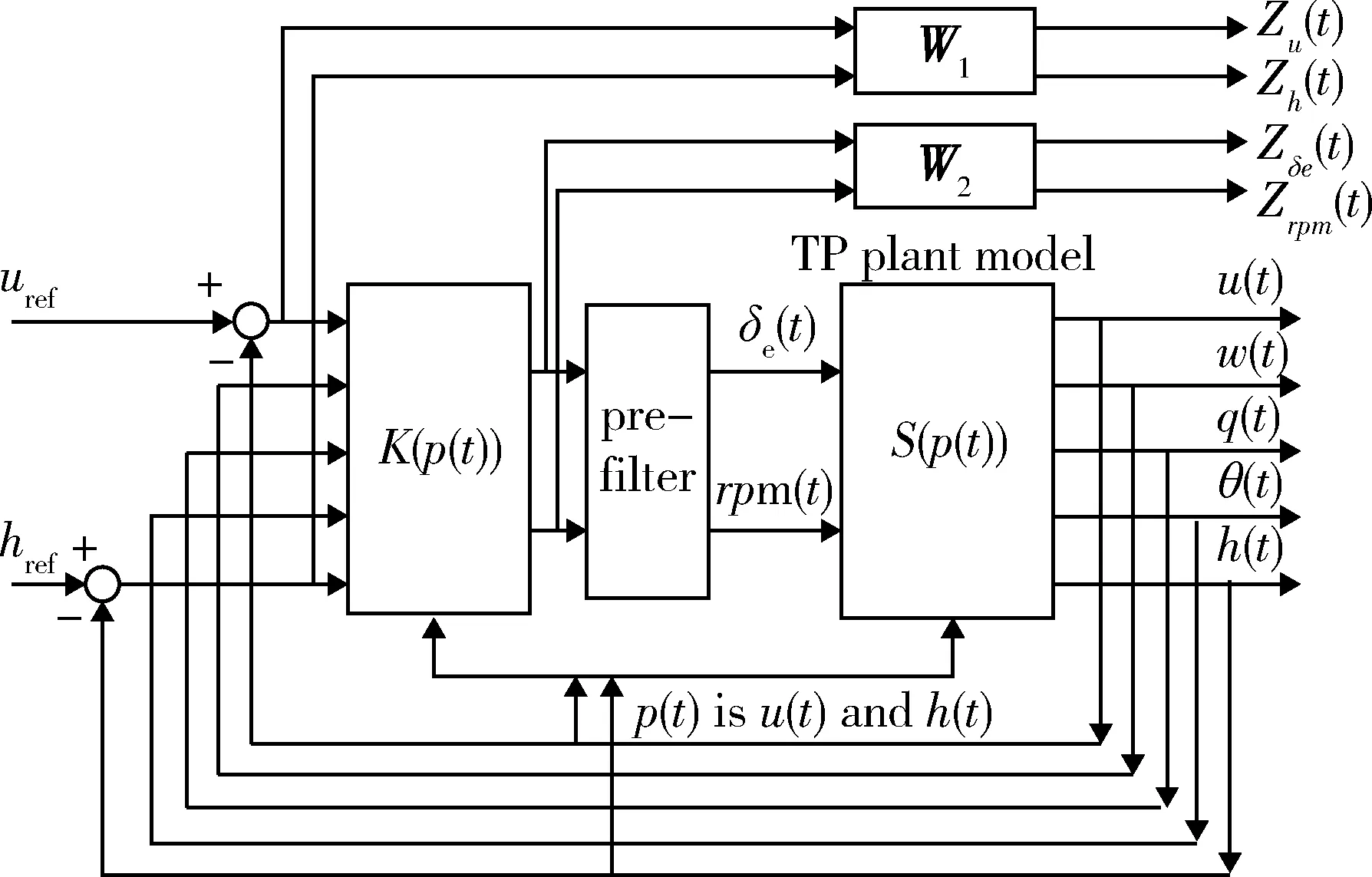
图4 纵向TP凸多面体对象模型的加权开环结构图Fig.4 Weighted open-loop structure diagram of longitudinal TP convex polyhedron object model

在扩展了纵向TP凸多面体模型之后，由式(38)～(40)，及加权函数W1和W2，可以使用例程hinfgs来合成LPV控制器。作为hinfgs的结果，得到了γ=3.039 5的LPV控制器。一旦从例程hinfgs中获得了LPV控制器的20个LTI顶层系统矩阵，就可以通过与构建TP凸多面体模型相同的方式以顶层系统矩阵和加权函数wa(p(t))的组合来构造该LPV控制器，由此得出，

(45)

为了确认达到混合灵敏度标准式(41)，在所有θ∈Θ(θ的冻结值)上计算传输矩阵S和KS的奇异值，如图5中所示。显然，S和KS的奇异值分别由W1和W2塑造和约束。

图5 ∀θ∈Θ上S和KS的奇异值(θ的冻结值)Fig.5 singular values of S and KS on ∀θ∈Θ (freezing value of θ)

图6 W1S和W2KS在∀θ∈Θ(带冻结的θ)上的H∞范数Fig.6 H∞norm of W1S and W2KS on ∀θ∈Θ (θ with freezing)

图7 某型固定翼无人机非线性动力学模型对H∞增益调度 自动驾驶仪的高度瞬态性能响应曲线Fig.7 Altitude transient performance response curve of a fixed-wing UAV nonlinear dynamics model to H∞ gain scheduling autopilot

图8 某型固定翼无人机非线性动力学模型对H∞增益调度 自动驾驶仪的速度瞬态性能响应曲线Fig.8 Speed transient performance response curve of a fixed-wing UAV nonlinear dynamics model to H∞ gain scheduling autopilot

3 某型无人机六自由度非线性仿真分析结果

在MATLAB SIMULINK仿真环境下，针对某型固定翼无人机设计了H∞增益调度自动驾驶仪，并对其非线性数学模型进行了验证。仿真中用到的所有20个加权函数wa(p(t))，均使用二维查表来构造。在图7～13中，给出了模拟飞行器在飞行包线中某一特定点(无人机速度为506 ft/s，高度为10 000 ft)的高度和速度以及俯仰角、俯仰角速率、迎角、升降舵偏转角、发动机转速微小要求变化时的瞬态响应。对于飞行包线中的其他点，也得到了类似的响应。在图9～13中，在特定点验证H-∞增益调度自动驾驶仪Jinarink非线性动力学模型瞬态性能。响应曲线主要考核无人机飞行控制系统的瞬态响应能力以及无人机飞行姿态变化和发动机性能之间的联系。

图9 某型固定翼无人机非线性动力学模型对H∞增益调度 自动驾驶仪的俯仰角瞬态性能响应曲线Fig.9 Pitch angle transient performance response curve of a fixed-wing UAV nonlinear dynamics model to H∞ gain scheduling autopilot

图10 某型固定翼无人机非线性动力学模型对H∞增益调度 自动驾驶仪的俯仰角速率瞬态性能响应曲线Fig.10 Pitch rate transient performance response curve of a fixed-wing UAV nonlinear dynamics model to H∞ gain scheduling autopilot

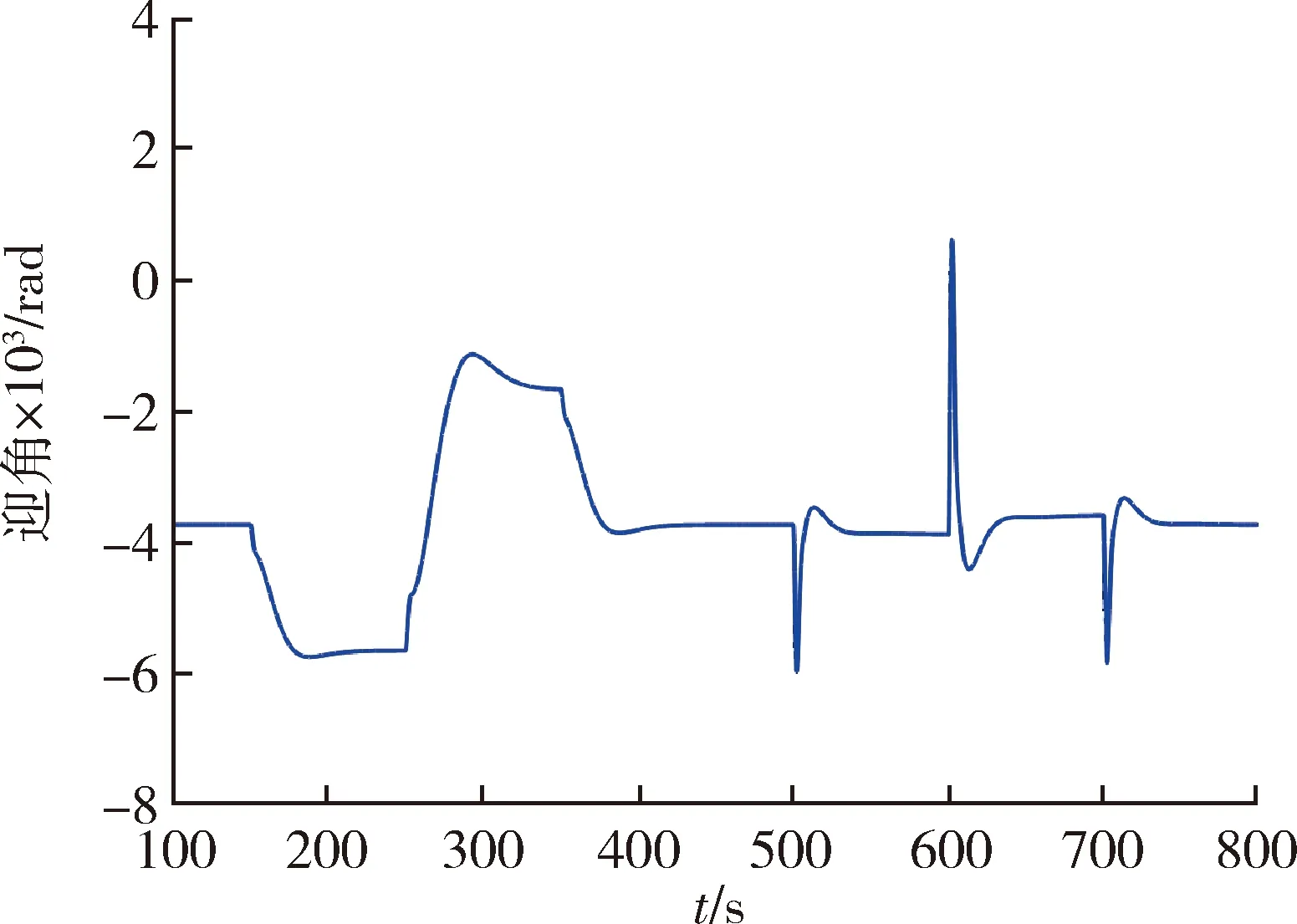
图11 某型固定翼无人机非线性动力学模型对H∞增益 调度自动驾驶仪的迎角瞬态性能响应曲线Fig.11 Angle of attack transient performance response curve of a fixed-wing UAV nonlinear dynamics model to H∞ gain scheduling autopilot

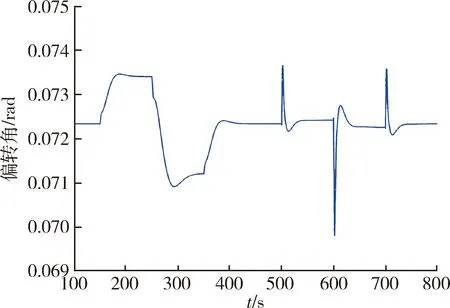
图12 某型固定翼无人机非线性动力学模型对H∞增益 调度自动驾驶仪的升降舵偏转角瞬态性能响应曲线Fig.12 Elevator deflection transient performance response curve of a fixed-wing UAV nonlinear dynamics model to H∞ gain scheduling autopilot

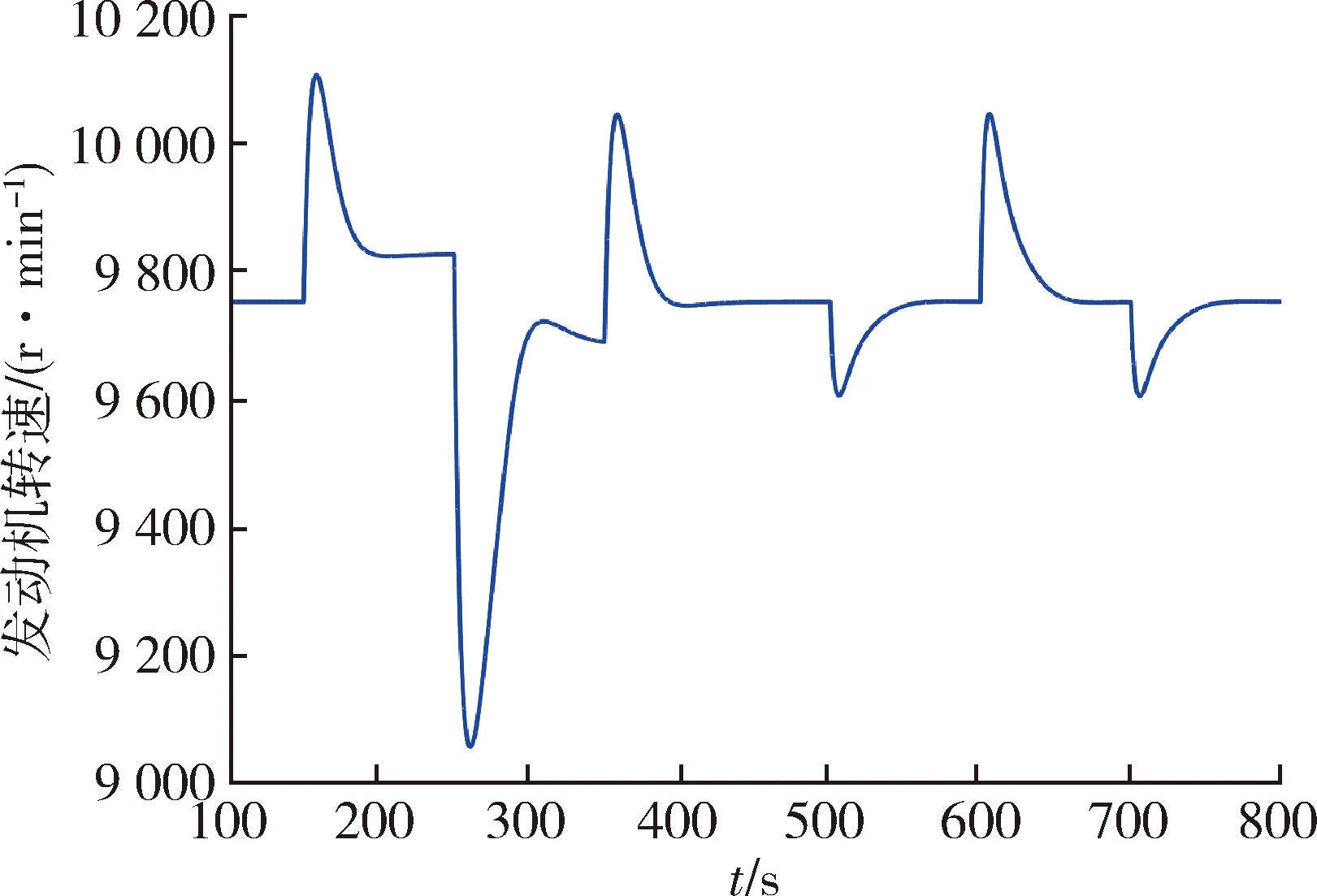
图13 某型固定翼无人机非线性动力学模型对H∞增益 调度自动驾驶仪的发动机转速瞬态性能响应曲线Fig.13 Engine speed transient performance response curve of a fixed-wing UAV nonlinear dynamics model to H∞ gain scheduling autopilot

在俯仰角、俯仰角速率、迎角、升降舵偏转角、发动机转速发生微小变化时，从曲线可知本文研究的H∞增益调度自动驾驶仪控制系统动态响应性能符合预期，控制系统快速性与准确性能够得到保证。

图14～20显示了覆盖大范围飞行包线的模拟飞行。结果表明，闭环控制系统在给定的飞行包络范围内稳定性和鲁棒性都达到了设计要求。

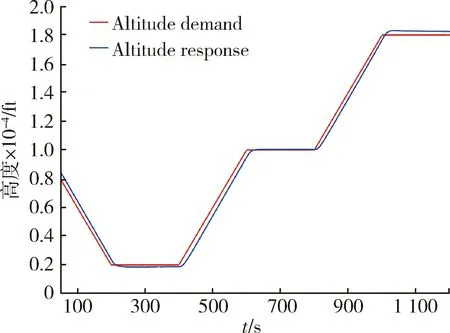
图14 给定飞行包线内闭环系统的高度特性曲线Fig.14 Altitude characteristic curve of a closed-loop system in a given flight envelope

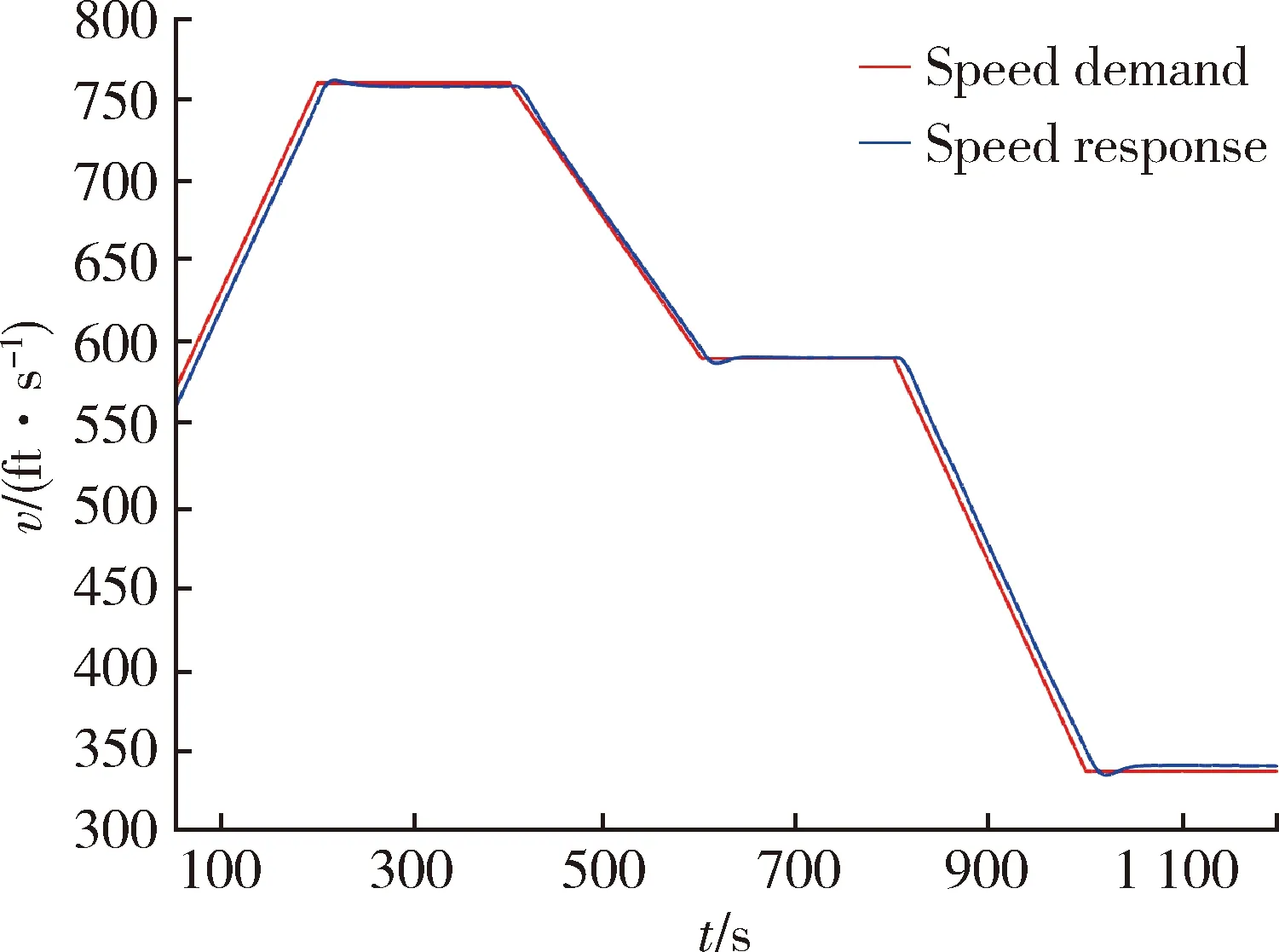
图15 给定飞行包线内闭环系统的速度特性曲线Fig.15 Speed characteristic curve of a closed-loop system in a given flight envelope

图16 给定飞行包线内闭环系统的俯仰角特性曲线Fig.16 Pitch angle characteristic curve of a closed-loop system in a given flight envelope

图17 给定飞行包线内闭环系统的俯仰角速率特性曲线Fig.17 Pitch rate characteristic curve of a closed-loop system in a given flight envelope

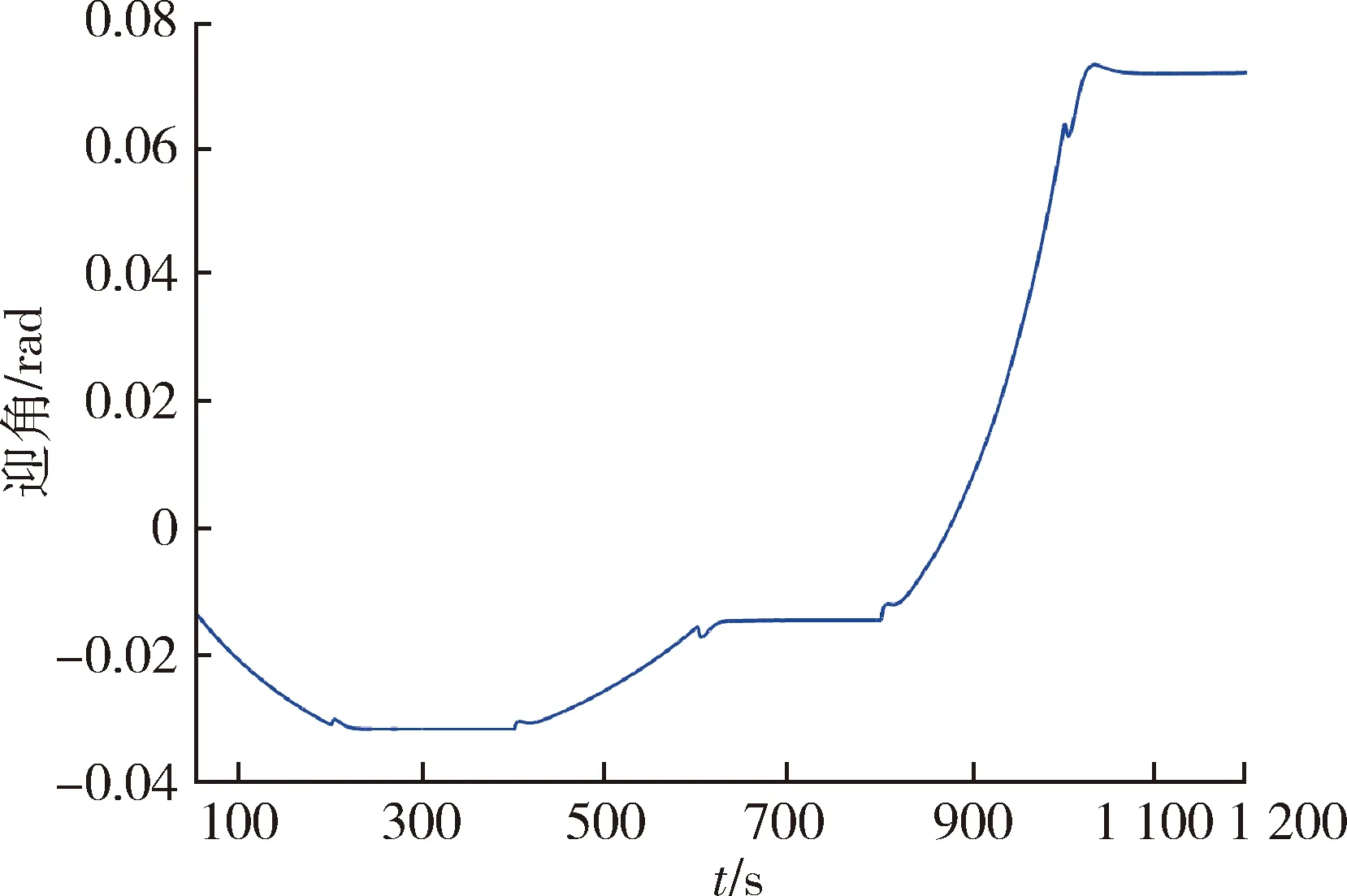
图18 给定飞行包线内闭环系统的迎角特性曲线Fig.18 Angle of attack characteristic curve of a closed-loop system in a given flight envelope

图19 给定飞行包线内闭环系统的升降舵偏转角特性曲线Fig.19 Elevator deflection characteristic curve of a closed-loop system in a given flight envelope

图20 给定飞行包线内闭环系统的发动机转速特性曲线Fig.20 Engine speed characteristic curve of a closed-loop system in a given flight envelope

由图14～20可知，当自动驾驶仪跟踪速度需求时，存在高度调节效果，当自动驾驶仪跟踪高度需求时，也存在速度调节效果，这是因为纵向TP多面体模型是准LPV模型，其中调度参数(速度和高度)也是系统的状态。这是准LPV模型在使用单个二次Lyapunov函数合成LPV控制器时的常见问题，因为参数变化率与系统状态的变化速度一样快。

4 结束语

本文采用LPV控制方法设计了常规固定翼无人机的鲁棒增益飞行控制器。针对传统增益调度技术在许多无人机应用中存在的昂贵和耗时的缺点，本文通过研究某型固定翼无人机在MATLAB SIMULINK环境下的六自由度非线性模型，应用张量-乘积(TP)模型变换方法，将非线性参数依赖的LPV模型转换为TP型凸多面体模型，构建了纵向非线性参数相关的无人机LPV模型的凸多面体表示。将增益调度输出反馈H∞控制器设计方法应用于所得到的TP凸多面体模型，得到了保证闭环系统在整个定义的飞行包线范围内具有较好稳定性、鲁棒性和优良性能的控制器。对该控制器进行了全六自由度的飞行器仿真试验，结果表明本文提出的LPV控制器既能处理六自由度非线性模型的不确定性，又能处理非线性，具有良好的指令跟随性、良好的干扰抑制能力、对测量噪声的低灵敏度、合理的小控制量和对附加对象扰动鲁棒稳定的特点，在所定义的飞行包线范围内，都达到了期望的稳定性能和鲁棒性目标。