基于Post-LASSO方法的大类资产因子配置研究

周亮 李宁

摘   要：基于因子的配置方法将资产配置的决策过程从资产层面转换为更为微观的因子层面，投资者能够通过对因子收益分布及相关性的预测更好地进行资产配置。选择包括经济增长、通货膨胀、市场因子、规模因子和盈利因子在内的宏观和风格因子，以及股票、债券和商品在内的多种资产指数的月度数据，基于Post-LASSO模型和Greenberg等（2016）稳健性最优化算法检验了基于因子的大类资产配置方法在我国的可应用性。研究结果发现：通过因子权重映射的资产组合能够较好地模拟出各因子的初始权重，Post-LASSO方法能够取得显著优于传统OLS方法的映射效果;映射资产组合的收益走势可以对因子组合进行部分追踪，但是由于因子收益率和资产收益率存在着较大差异，因此，两个组合的净值走势也存在着一定偏差。研究结论丰富了投资组合的相关理论，也为投资者从传统资产配置转向因子配置提供了经验借鉴。

关键词：因子配置;资产配置;投资组合;Post-LASSO

中图分类号：F830  文献标识码：B  文章编号：1674-2265（2021）11-0039-09

DOI：10.19647/j.cnki.37-1462/f.2021.11.006

一、引言与文献综述

传统的资产配置方法通常是基于各个资产的收益、风险特征，利用均值—方差最优化等方法确定资产的最优权重，在实践过程中存在着一定不足（Jagannathan和Ma，2003;Behr等，2013;谭华清等，2018;周亮和李红权，2019）[1-4]。首先，当市场出现极端下行情况时，资产相关性会大幅提升，许多资产的收益同步变动，此时传统资产配置方法未能有效分散风险。其次，传统资产配置方法通常未能对宏观经济环境的变化做出有效反应。通常的资产配置方法仅考虑了资产自身的收益风险特征，未根据宏观经济的变化调整资产权重。再次，当资产数目较多时，预测各资产的预期收益具有一定的困难，配置难度也会加大。最近的文献表明，相比股票、债券等不同类别的资产，系统风险因子也许能够成为多样化投资中一类更好的基石（Clarke等，2005;Bender等，2010;Page和Taborsky，2011）[5-7]，其中心思想是识别风险收益因子，并建立能够捕捉这类溢价的投资组合。

自Fama和French（1993）[8]提出三因子模型以来，因子投资便成为投资理论研究及实践应用的焦点，之后大量新的因子被提出并得到广泛应用。典型的如Carhart（1997）[9]基于美国共同基金数据提出了动量因子（李富军等，2019）[10]，Amihud（2002）[11]基于换手率数据提出了非流动性因子，Ang等（2006）[12]在发现了低风险异象基础上提出的异质波动率因子（Frazzini和Pedersen，2014;周亮和王银枝，2020）[13-14]，Fama和French（2015）[15]在三因子的基础上增加了投资因子和盈利因子构造了五因子模型等（赵胜民等，2016）[16]。Harvey等（2016）[17]发现在顶级金融学术期刊和SSRN高評价工作论文上的定价因子多达316个。但是这么多因子并不都是有效的，Green等（2017）[18]和Hou等（2020）[19]的研究发现，大部分因子在后续的样本外检验中难以持续地提供超额收益。因子配置方法的挑战在于如何识别和生成与传统资产预测模型一样稳健的因子预测模型，以及如何通过最优化方法获得与因子配置预期目标偏差最小的资产配置投资组合。Blyth等（2016）[20]以及Greenberg等（2016）[21]通过时间序列回归（有时加上自由判断）来估计因子的暴露，以确保资产对预先确定的因子集具有直观的暴露，从而得到较好的因子映射结果。

基于因子的配置方法将资产配置的决策过程从资产层面转换为更为微观的因子层面，投资者能够通过其对因子收益分布以及相关性的预测更好地进行资产配置（Idzorek和Kowara，2013;Kelley等，2014;Bass等，2017）[22-24]。基于因子的资产配置方法具有诸多优势：首先，基于因子的资产配置方法可以识别出风险与收益的关键驱动因素，并根据关键驱动因素进行资产的有效配置，在宏观经济出现变化时，可以及时有效地对宏观经济的变化做出反应（Ang，2010;Bender等，2019）[25，26]。其次，基于因子的资产配置方法可以更好地分散风险。在识别出不同资产的共同驱动因素之后，可以利用因子进行有效地分散化，提升资产组合的收益风险比。再次，基于因子的方法将资产配置决策从较大的资产范围转换为较小的因子范围，可以提升资产配置的效率。在资产种类较多时，少量的因子就可以驱动大批资产的回报，投资者只需要对少量因子的收益、风险、相关性进行预测，就可以对大量资产进行配置，这样可以使得资产配置过程更加高效。

基于此，本文拟选择最常见的宏观因子（包括经济增长和通胀因子）及风格因子（Fama五因子以及动量因子）进行因子配置，并通过Greenberg等（2016）[21]的最优化目标函数将因子权重映射到资产上，以实现可投资的资产配置组合。相对于其他学者的研究，本文的创新之处在于：第一，采用Post-LASSO方法确定资产的因子载荷矩阵，相对于普通OLS的回归结果，Post-LASSO方法通过自变量的筛选以及对回归系数更精确地估计，可以更准确地估计出资产与因子间的映射关系;第二，对Greenberg等（2016）[21]的最优化目标函数进行了探索和扩展，如对[γ]系数的稳健性估计、加入收益项、去除资产协方差项等，以寻求映射关系更稳健的估计。

二、研究设计

（一）因子载荷矩阵确定模型

根据多因子模型（Fama和French，2015;赵胜民等，2016）[15，16]，资产的收益率可以分解到一系列因子收益率上，用公式表示如下：

其中，[rt]为一系列资产的收益率向量，[ft]为因子的收益率向量，[A]为资产的因子载荷矩阵（也可以称为因子暴露、因子映射等），[εt]为残差项，其期望为0。

一般可以采用线性回归的方法求出因子载荷矩阵[A]，但是考虑到当因子数量较多时，因子之间可能存在着共线性，从而导致回归结果与实际情况会存在一定偏差。因此，本文拟采用Post-LASSO方法对因子载荷矩阵[A]进行估计。

LASSO模型是在普通最小二乘法的目标函数中增加L1正则项，以将不重要变量前的系数压缩为0，从而实现变量筛选和选择的功能。具体而言，其目标函数如式（2）所示，

其中，[L（θ）]为最小二乘的目标函数，[j=1Pθj]为L1正则项，[λ]是正则项的惩罚系数，[λ]越大，目标函数中惩罚项所占权重越高，更多的变量系数会被压缩到0，反之亦然。[λ]值由K折交叉验证法自动筛选。

考虑到LASSO方法中的正则项会对所有变量的系数起到一定的压缩作用，因此，Belloni和Chernozhukov（2013）[27]提出了Post-LASSO方法。该方法分为两个步骤：第一步，用LASSO模型进行特征选择;第二步，再用LASSO模型中系数不为零的变量进行一次线性回归或者逻辑回归，从而实现对变量系数更准确地估计。本文采用Post-LASSO方法对所有资产的因子载荷进行估计。

（二）最优资产权重计算方法

按照Greenberg等（2016）[21]的稳健性最优化算法，对于N个资产类别与K个因子，最优化的目标式可以表示为：

其中，[wp]为N个资产的权重向量，[A]为[N×K]的资产对各因子的暴露矩阵，[P]为[K×K]的因子协方差矩阵，[Q]为[N×N]的资产协方差矩阵，[ep]为目标因子配置比例，[γ]为目标函数中的方差成分权重。Greenberg等（2016）[21]将[γ]设为0.99，即几乎将全部权重放在最小化投资组合的波动上。后续研究中我们同样将[γ]设为0.99，并同时对[γ]进行多重取值以进行稳健性检验。值得说明的是，由于我们选择的资产数量并不是很多，因此，未充分参照Greenberg等（2016）[21]原文中约束[wi≥0]，而是设定[-0.5≤wi≤0.5]，即可以对部分资产进行做空。实际上，如果限制做空，跟踪效果会非常差，一定程度上放松做空条件，可以使跟踪效果大幅上升。

除了式（3）的目标函数形式外，本文还考虑了两个变形形式，分别如式（4）和式（5）所示：

其中，式（4）中增加了资产的收益项，[r]是资产的历史平均收益率，以实现风险与收益的均衡;式（5）中去掉了资产自身的协方差矩阵，将几乎所有权重都放在了对目标因子权重的跟踪。后续研究将检验这两种变形的目标函数对跟踪效果及投资绩效的影响。

（三）因子配置模型

为了检验因子映射的效果，本文分别选择等权重、风险平价及均值—方差最优化组合模型三种因子配置模型。

等权重是对所有待投资因子赋予相同权重，即[wi=1K]，K为因子的数量。

风险平价模型是将风险在各资产（因子）之间进行平均分配。每种资产（因子）在资产（因子）组合中的风险比率为[pi=wi∂σp∂wiσp]。其中，[σp]为资产（因子）组合的波动率，当所有[pi]均相等时，即为风险平价组合。在实践中，由于资产（因子）之间的相关性并不稳定，且估计误差往往比波动率的估计误差大，因此，很多时候采用波动率的反比关系来确定各资产（因子）的权重，且得到的计算结果往往比更复杂的运算结果更为可靠（Lee，2014）[28]。考虑到本文中因子相关性较低，因此，风险平价组合直接用波动率倒数模型来构造。

均值—方差最优化组合模型是通过最大化风险调整后收益的方式求得资产（因子）的最优配比，目标函数为[argmin12δwTPw-WTμ]，其中[δ]为风险规避系数，此处设定为2，[μ]为因子的历史平均收益率。

（四）变量选取及说明

本文选择了2个宏观经济因子，包括经济增长和通货膨胀，其中，经济增长采用PMI指数来衡量，通货膨胀采用30%的CPI和70%的PPI加权合成，以综合反映生活和生产资料的物价状况。同时初步选择了6个风格因子，包括Fama五因子（市场因子MKT、规模因子SMB、价值因子HML、盈利因子RMW及投资因子CMA）以及Carhart动量因子UMD。因子的映射资产选择了包括股票、债券及商品在内的多个指数，其中股票包括沪深300、中证500、中证1000以及巨潮的9个行业指数，债券包括中证国债、中证企业债以及中证转债，商品包括南华农产品、南华金属、南华能化以及黄金指数。选取所有因子及资产2005年1月—2020年11月的月度数据进行分析，宏观因子和资产数据来自万得数据库，因子数据来自锐思数据库。

三、实证检验与分析

（一）变量描述性统计及相关性分析

表1报告了所有因子及资产在样本区间的描述性统计分析结果。从Panel A可以看到，宏观因子表现相对稳定，标准差显著低于风格因子，经济增长因子和通货膨胀因子的一阶自相关系数分别高达0.7和0.97，而风格因子的自相关系数均低于0.15，HML和UMD的自相关系数甚至为负，说明这两个因子会出现短期反转。从收益来看，市场因子的收益最高，年化收益率达到了15.33%;而HML、CMA和UMD三个因子的年化收益率为负，说明这三个因子在样本区间内整体无效，因此，后续研究中我们將这三个风格因子剔除，只选择了经济增长、通货膨胀、市场、规模及投资五个因子进行分析。从Panel B资产的描述性统计分析可以看到，股票的收益率相对较高，尤其是规模越小的股票指数（中证1000）收益越高。国债和企业债的收益不高，但是它们的风险很低;转债具有一定的股性，其收益率和风险均接近股票。商品中金属和黄金表现较为优秀，年化收益率均超过了10%;相对来说，农产品和能化表现一般。从股票的行业指数来看，消费和医药表现相对较好，而能源和公用表现相对较差。除了国债和企业债外，其他所有资产指数的一阶自相关系数均小于0.18，说明资产收益率的自相关性不高，远低于宏观因子。

表2报告了变量的相关系数矩阵，其中Panel A是因子间的相关系数，Panel B是部分资产间的相关系数。可以看到，因子间的相关性较低，最高的为经济增长与通货膨胀间的0.21，且部分因子间存在着显著的负相关关系，如规模因子和盈利因子间的相关系数为-0.71;而资产间的相关系数较高，除中证国债与其他资产间的关系为负外，其他资产间的相关系数均显著为正，且数值较高，其中沪深300与中证1000的相关系数高达0.78、与中证转债的相关系数高达0.77。因此，采用因子配置来构造投资组合，能够比通过资产配置，取得更好的分散化效果，这也是本文研究基于因子的资产配置的出发点。

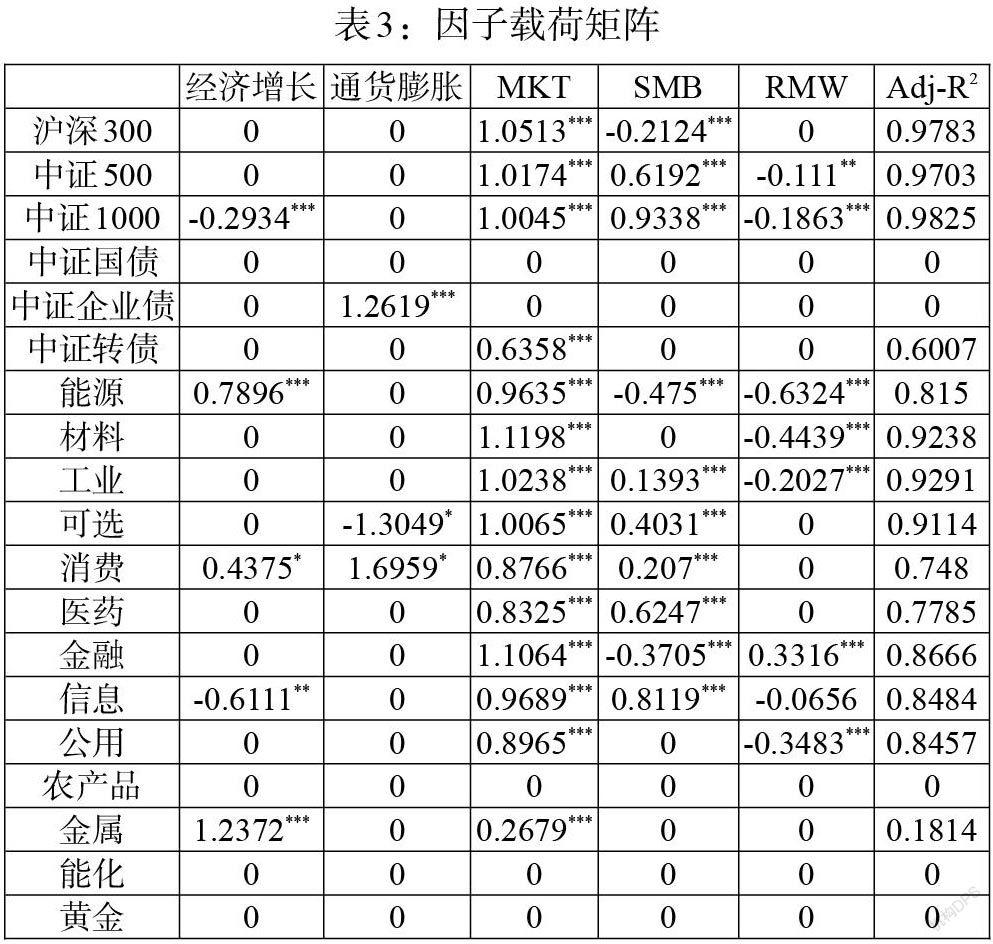
（二）因子载荷矩阵计算

采用Post-LASSO方法，我们计算出每种资产的因子载荷，得到结果如表3所示。可以看到，我们所选的5个因子对大部分股票指数的拟合效果均较好，表现为股票指数的调整R2均大于0.75（消费指数的R2略低于0.75）;5个因子对国债和企业债的拟合能力为0，这可能是因为国债和企业债主要受到货币供给和市场利率的影响，由于我们的宏观因子并没有包含相关因子，因此，对国债和企业债的解释能力非常弱;中证转债由于股性很强，市场因子对其具有较强的解释能力，调整R2高达0.6;商品中只有金属能够被经济增长因子和市场因子所解释，其调整R2为0.18，而农产品、能化及黄金指数均不能被所选5个因子解释。因此，接下来的研究中，我们仅采用股票指数、中证转债以及金属指数进行大类资产配置。

（三）因子权重设置及映射

我们利用式（3）的映射函数将因子配置映射到资产配置上。为了检验资产映射的效果，我们设定了三种因子配置方法，分别是等权重、风险平价以及均值—方差最优化组合。为了防止风险平价模型和均值—方差最优化组合模型中某些因子的权重过低，我们对这两个模型均设定了一个约束条件——所有因子权重不低于10%。三种因子配置方法的因子权重如表4所示，可以看到，风险平价模型在通货膨胀上有最高的权重，均值—方差最优化组合在市场因子上有最高的权重。

我们利用式（3）计算得到资产配置权重，并将其与因子载荷矩阵相乘，得到资产权重所代表的因子权重。结果如图1所示，其中浅灰色柱为初始因子权重，深灰色柱为通过Post-LASSO方法得到的资产权重反推的因子权重，白色柱是采用OLS得到的资产权重反推的因子权重。可以看到，等权重组合的Post-LASSO因子映射权重分别为18.66%、21.26%、27.24%、18.11%和19.30%，风险平价组合的因子映射权重分别为16.38%、57.27%、23.94%、11.40%和12.87%，均值—方差组合的因子映射权重分别为10.43%、10.3%、47.03%、13.41%和12.2%。与表4相比发现，三个组合通过资产映射的因子权重与初始因子权重相差较小，同时Post-LASSO映射模型能够比OLS模型获得更好的映射效果，等权重和风险平价组合中Post-LASSO模型的映射偏差仅为OLS模型的一半左右（采用标准偏差[15i=15（wi-wPi）]衡量，[wi]和[wPi]分别表示映射的因子权重以及初始的因子权重），均值—方差模型中两者大体相似。因此，综合来看，基于Post-LASSO映射模型能够更好地将因子权重映射到资产权重上。

我们基于Greenberg等（2016）[21]的研究，将式（3）中的[γ]设定为0.99，即几乎把全部权重放在最小化投资组合的波动上。为了检验结果的稳健性，表5中我们考察了[γ]分别设定为0.01、0.5和0.99时对因子映射权重的影响。从Panel A可以看到，相对于表4中因子初始权重，[γ]等于0.01和0.5时的结果更为稳健，其相对基准的标准偏差均要小于[γ]取0.99时的计算结果。从Panel B中可以看到，[γ]等于0.01和0.5时因子权重所映射的资产权重间差异较小，但是[γ]等于0.99时的资产权重与之存在一定差异，这主要是因为[γ]等于0.99时为组合波动赋予了更多的权重，对组合波动及风险调整后收益的提高有一定帮助，但是会导致因子映射权重存在一定偏差。考虑到很多文献都证明了低波动异象的广泛存在（Frazzini和Pederson，2014;周亮和王银枝，2020）[13，14]，因此，后续实证研究中我们将遵照Greenberg等（2016）[21]的做法，将[γ]设定为0.99，并考察基于因子的资产配置效果，在后续资产配置绩效分析中我们将会对[γ]的设定再次进行稳健性检验。

（四）静态投资结果与分析

采用因子等权重（Equal）、风险平价（RP）、均值—方差最优化组合（MVO）三种因子权重及其映射的三种资产权重（Map_Equal、Map_RP、Map_MVO）构造投资组合，表6报告了这6种投资组合绩效的描述性统计分析及相关性分析结果。从表6的Panel A可以看到，相对于等权重组合，风险平价组合的风险水平更低，但是收益也略低于等权重组合，而均值—方差最优化组合的收益和风险均远高于等权重组合。因子权重映射的资产配置组合的收益和风险均高于对应的因子投资组合。从Panel B可以看到，三种因子配置组合间的收益相关系数均在0.92以上，三种资产配置组合间的收益相关系数均在0.83以上，说明不同配置策略间的相关性较强;同时因子配置组合与资产配置组合间的相关系数大部分在0.4以上，但均小于0.8。因此，综合来看，通过将因子权重映射到资产权重，可以部分实现对因子投资组合的复制和跟踪，但是由于本文所选资产数量并不多且在映射公式中對资产自身波动赋予一定的权重，导致资产配置组合和投资组合间存在着一定差异。

图2报告了6种投资组合的净值走势，从Panel A可以看到，因子MVO组合获得了最高收益，其最终净值达到了4.56，远高于其他两个因子组合，但是波动率也高于其他两个因子组合。从Panel B可以看到，映射的三种资产配置间走势相差并不大，等权重因子映射的资产组合最终净值达到8.02，略高于其他两个组合。总体而言，因子权重映射的资产组合可以对因子组合进行追踪，且从图上发现净值曲线走势存在着较强的相关性，但是在运行过程中存在着一定偏差，导致最终净值差异较大。

（五）动态投资结果与分析

上一节是采用静态方式进行资产配置，即将样本内的因子权重设为固定值，再将其映射到固定的资产权重上进行配置，在现实投资中并不具备可操作性。本节采用动态配置方法，将滚动窗口设定为60个月（即5年），先用t-60～t-1期的因子收益和资产收益构造因子等权重、风险平价及均值—方差最优化投资组合。再将其映射到不同的资产权重，并在第t期按照计算出的因子权重和资产权重进行配置;再用t-59～t期的收益对t+1期的因子權重和资产权重进行设定并构造投资组合;依此类推。表7报告了动态投资组合的绩效表现，可以看到，相对于静态投资组合，动态组合的收益和风险均有所降低，这是因为权重的动态调整能够更快适应市场节奏的变化，从而带来风险的降低，但是由于静态组合属于事后验证，因此，收益率相对较高。风险平价组合的风险仍然是最低的，而均值—方差最优化组合的风险仍然最高。从Panel B相关性分析结果可以看到，三种资产配置组合间的相关性较高，与等权因子及风险平价因子组合间的相关系数均在0.45以上，但是与均值—方差最优化因子组合的相关系数普遍只有0.3左右。综合来看，与静态配置组合的结论较为相似，动态配置组合通过将因子权重映射到资产权重，可以部分实现对因子投资组合的复制和跟踪，但是两者之间也存在着一定差异。

从图3的动态配置组合净值走势图也可以看到，三种因子配置组合的走势大体相似，但是净值曲线也存在着明显差异，其中等权重因子组合最终净值最高，达到1.58;三种资产配置组合的相关性较强，与等权重、风险平价组合相比，均值—方差最优化资产组合收益更高，其最终净值达到2.5。综合来看，因子权重映射的资产组合可以对因子组合进行部分追踪，但是也存在着一定差异。

（六）目标函数对资产配置的影响

本节我们检验目标函数的不同参数及不同形式对资产配置效果的影响。表8报告了检验结果，Panel A反映的是改变[γ]参数设定后的结果，其中，Equal0.01、VolInv0.01和MVO0.01将[γ]参数设定为0.01，Equal0.5、VolInv0.5和MVO0.5将[γ]参数设定为0.5;Panel B是改变了目标函数形式后的结果，其中，Equal2、VolInv2和MVO2在目标函数中加入了资产的收益项（见式（4）），Equal3、VolInv3和MVO3去掉了目标函数中资产的协方差项。Panel A和Panel B中“相关系数”行均为该列所代表的资产配置组合与其对应的因子配置组合间的相关系数。可以看到，将[γ]参数设定为0.01和0.5时，资产配置组合的收益率和波动率均略有提高，与对应的因子配置组合的相关系数大体相当。与表5的结论相似，不同的[γ]参数会导致因子映射权重存在一定偏差，从而使得资产组合的收益存在差异，但是差异并不明显。Panel B的结果显示，加入资产收益项后，资产配置组合的年化收益率有了大幅提升，但是风险也大幅增加。除风险平价组合外，等权组合和均值—方差最优化组合的夏普比率均有了明显下降，但是三个组合与相应因子配置组合的相关系数均有了一定上升;去掉目标函数中资产的协方差项后，资产配置组合的收益有了一定下降，且风险出现了大幅上升，虽然与相应因子配置组合的相关系数有一定上升，但是夏普比率均出现了明显下降。因此，综合来看，[γ]参数虽然对映射的资产权重有一定影响，但是不会带来显著差异;去掉目标函数的资产协方差项会导致资产配置组合的夏普比率大幅下降，并不合适;但是如果在目标函数中增加资产的收益项，可以提高资产配置组合的投资收益，只是风险也会显著上升。

四、结论与讨论

选择包括经济增长、通货膨胀、市场因子、规模因子和盈利因子在内的5个宏观和风格因子，以及股票、债券和商品的多种资产指数2005年1月—2020年11月的月度数据，基于Post-LASSO模型和Greenberg等（2016）[21]的稳健性最优化算法检验了基于因子的大类资产配置方法在我国的可应用性。研究结果发现：通过因子权重映射的资产组合能够较好地模拟出各因子的初始权重，Post-LASSO方法能够取得显著优于传统OLS方法的映射效果;映射资产组合的收益走势可以对因子组合进行部分追踪，但是由于因子收益率和资产收益率存在较大差异，因此，两个组合的净值走势也存在一定偏差;[γ]参数的变化对因子映射的结果有一定影响，但是不会带来显著差异，后续研究可以对[γ]参数进行更精细的分析;通过改变目标函数的形式（如增加收益项或去除资产协方差项），并不能带来投资绩效的提高，主要是因为对未来收益预测的难度以及低风险异象的广泛存在性，通过Greenberg等（2016）[21]稳健性最优化算法及[γ]参数的微调可能是实现因子映射较合适的方法。

本研究是对投资组合理论的有力补充，同时对于金融投资实践也有着较强的指导意义：第一，从传统的资产配置转向因子配置可以实现投资收益和风险的相对改善，且能够通过更加定量化的方法对投资流程进行标准化和程序化，从而避免人为主观操作对投资绩效带来的损害。第二， 识别有效因子是进行因子配置的关键前提，如本文中所选因子中，投资因子、动量因子等并不能获得正收益，说明这些因子在我国资本市场有效性并不强，如果将过多的权重配置在这些因子上，不仅不能获得分散投资的优势，而且极可能带来投资收益的显著下降，因此，在构建因子组合前，应认真挑选具有有效性及可投资性的因子。第三，将因子权重映射到资产的权重上是实现因子投资的关键步骤，因此，需要挑选合适的资产来进行投资，比如通过个股来对风格因子进行映射时效果往往会更好，但可能会导致换手率过高等问题，在对宏观因子进行映射时选择大类资产的效果可能更好。

参考文献：

[1]Jagannathan R，Ma T. 2003. Risk Reduction in Large Portfolios：Why Imposing the Wrong Constraint Helps [J]. Journal of Finance，58（4）.

[2]Behr P，Guettler A，Miebs F. 2013. On Portfolio Optimization：Imposing the Right Constraints [J].Journal of Banking & Finance， 2013，37（4）.

[3]谭华清，赵学军，黄一黎.动量思想与大宗商品的战术配置价值——基于Black-Litterman模型 [J].经济理论与经济管理，2018，（10）.

[4]周亮，李红权.投资时钟原理及战术资产配置在投资组合管理中的应用——基于修正Black-Litterman模型 [J]. 中央财经大学学报，2019，（10）.

[5]Clarke R，de Silva H，Murdock R. 2005. A Factor Approach to Asset Allocation [J].Journal of Portfolio Management，32（1）.

[6]Bender J，Briand R，Nielsen F，Stefek D. 2010. Portfolio of Risk Premia：A New Approach to Diversification [J]. Journal of Portfolio Management，36（2）.

[7]Page S，Taborsky M A. 2011. The Myth of Diversification：Risk Factors Versus Asset Classes [J].Journal of Portfolio Management，37（4）.

[8]Fama E F，French K R. 1993. Common Risk Factors in the Returns on Stocks and Bonds [J].Journal of Financial Economics，33（1）.

[9]Carhart M M. 1997. On Persistence in Mutual Fund Performance [J].Journal of Finance，52（1）.

[10]李富军，姜富伟，杨桦.投资者理性特征对动量效应的影响——基于中国A股市场的证据 [J].宏观经济研究，2019，（11）.

[11]Amihud，Y. 2002. Illiquidity and Stock Returns：Cross-section and Time-series Effects [J]. Journal of Financial Markets，5（1）.

[12]Ang A，Hodrick R J，Xing Y，Zhang X. 2006. The Cross-Section of Volatility and Expected Returns [J].Journal of Finance，61（1）.

[13]Frazzini A，Pedersen L H. 2014. Betting Against Beta [J].Journal of Financial Economics，（1）.

[14]周亮，王银枝.中国股市低风险异象研究 [J].金融理论与实践，2020，（3）.

[15]Fama E F，French K R. 2015. Incremental Variables and the Investment Opportunity Set [J].Journal of Financial Economics，117（3）.

[16]趙胜民，闫红蕾，张凯.Fama-French五因子模型比三因子模型更胜一筹吗——来自中国A股市场的经验证据 [J].南开经济研究，2016，（2）.

[17]Harvey C R，Yan L，Zhu H Q. 2016. … and the Cross-Section of Expected Returns [J].Review of Financial Studies，29（1）.

[18]Green J，Hand J，Zhang X. 2017. The Characteristics that Provide Independent Information about Average U.S. Monthly Stock Returns [J].Review of Financial Studies，30（12）.

[19]Hou K，Xue C，Zhang L. 2020. Replicating Anomalies [J].Review of Financial Studies，33（5）.

[20]Blyth S，Szigety M，Xia J. 2016. Flexible Indeterminate Factor-Based Asset Allocation [J].Journal of Portfolio Management，42（5）.

[21]Greenberg D，Babu B，Ang A. 2016. Factors to Assets：Mapping Factor Exposures to Asset Allocations [J].Journal of Portfolio Management，42 （5）.

[22]Idzorek T M，Kowara M. 2013. Factor-Based Asset Allocation vs. Asset-Class-Based Asset Allocation [J].Financial Analysts Journal，69（3）.

[23]Kelley G，Kinlaw W，Thomas R. 2014. Practical Applications for Factor Based Asset Allocation [R].SSGA Working Paper.

[24]Bass R，Gladstone S，Ang A. 2017. Total Portfolio Factor，Not Just Asset，Allocation [J].Journal of Portfolio Management，43（5）.

[25]Ang A. 2010. The Four Benchmarks of Sovereign Wealth Funds [R].Columbia Business School and NBER Working Paper.

[26]Bender J，Sun J，Thomas R. 2019. Asset Allocation vs. Factor Allocation-Can We Build a Unified Method？[J]. Journal of Portfolio Management，45（2）.

[27]Belloni A，Chernozhukov V. 2013. Least Squares after Model Selection in High-dimensional Sparse Models [J]. Bernoulli，19（2）.

[28]Lee W. 2014. Constraints and Innovations for Pension Investment：the Cases of Risk Parity and Risk Premia Investing [J].Journal of Portfolio Management，40（3）.