义务教育阶段数学创新性考查要求的实施路径探析

【摘要】创新能力是贯彻立德树人、全面发展素质教育的重要目标。义务教育阶段，数学创新性考查要求聚焦与创新性高度关联的学科素养和关键能力，融入数学必备知识和数学思维，立足于数学的即用、知用、善用能力发展水平的检测，为实现“五育”并举、评价正确导向教学发挥筑牢着力点与支撑点。

【关键词】创新性考查;真实情境;关键能力;数学素养

作者简介：郭学金（1964.09-），男，湖北省钟祥市东桥镇黄集小学，一级教师，获钟祥市师德先进个人，论文获荆门市一等奖，课件获荆门市三等奖。

中共中央、国务院《关于深化教育教学改革全面提高义务教育质量的意见》在“提升智育水平”部分指出，“着力培养认知能力，促进思维发展，激发创新意识。”[1]中共中央、国务院印发的《深化新时代教育评价改革总体方案》在“深化考试招生制度改革”部分进一步指出，“加强科研创新能力和实践能力考查。”《全日制义务教育数学课程标准（实验稿）》在“课程目标”部分也明确指出，“具有初步的创新精神和实践能力，获得适应未来社会生活和进一步发展所必需的重要数学知识（包括数学事实、数学活动经验）以及基本的数学思想方法和必要的应用技能。”PISA（The Program for International Student Assessment，国际学生评估项目）将创新性思维定义为“能够有效参与创意的产生、评估和改进的能力，且这种能力可以形成新颖而有效的实际解决方案，能够促进学生知识的学习，并产生丰富的想象力” ，涵蓋创造性表达（文字表达、视觉表达）、知识创造以及创造性问题解决，体现新颖性、创造性、超越性和非重复性、价值性。简而言之，创新性强调独立思考和创新思维。

一、义务教育阶段数学创新性考查要求的实施依托

“五育”并举，全息育人，全面发展素质教育体系，凸显了对创新思维的培养。这就要求教师深入理解数学学科特点、知识结构与思想方法，科学把握学生的认知规律，激发学生的好奇心和想象力，培养学生的创新能力。

义务教育阶段数学主要的学习领域有“数与代数”“空间与图形”“统计与概率”“实践与综合应用”，属于学科必备知识。在学习必备知识的过程中，教师设计丰富多彩的教学活动，发展学生的数感、符号感、空间感、统计观念以及应用意识与推理能力，使学生初步学会运用数学的思维方式去观察、分析现实社会，解决生活实践问题和跨学科问题，发展学生应用数学的意识。创新是指学生面对真实生活中生产实践的问题时，能够适时地进行数学抽象，能够不受固有思维模式的束缚，以全新的视角看待问题，有别于按照常规思维提出问题的解决设想，并以此为纲，创造性地分析解决问题的一种过程。因此，数学抽象、数学应用、数学推理等学科关键能力应该是实施创新性考查的重要路径。

义务教育阶段全面践行立德树人、深化关键领域改革、全面提高教育质量目标的落实，必然要求义务教育阶段的数学命题关注未来社会要求人才所必备的学科素养。根据数学学科的学科特点及创新能力的本质意蕴，数学知识或方法的即用、知用、善用能力发展水平的检测是落实义务教育阶段数学创新性考查要求的三条具体实施路径。所谓即用，是学生能够立刻运用现场学习到的数学知识或方法解决问题;知用是指学生能够用数学关键能力及思维方法来分析、解决问题;善用则是学生能够从综合视角灵活调用数学必备知识解决问题。

二、义务教育阶段数学创新性考查要求的实施路径

义务教育阶段数学创新性考查要求实施的基本路径为：精心遴选适宜的真实情境素材，命制系统关联或拓展迁移的情境化试题，以学生在情境活动中的表现来真实反映其数学必备知识和关键能力的即用、知用与善用的能力发展水平，践行创新性考查要求。本文以PISA数学素养测试公开题作为案例进行深度剖析，以期为一线教师命制符合新时代要求的数学试题提供启发。

（一）基于会学、能用真实情境，检测即用能力发展水平

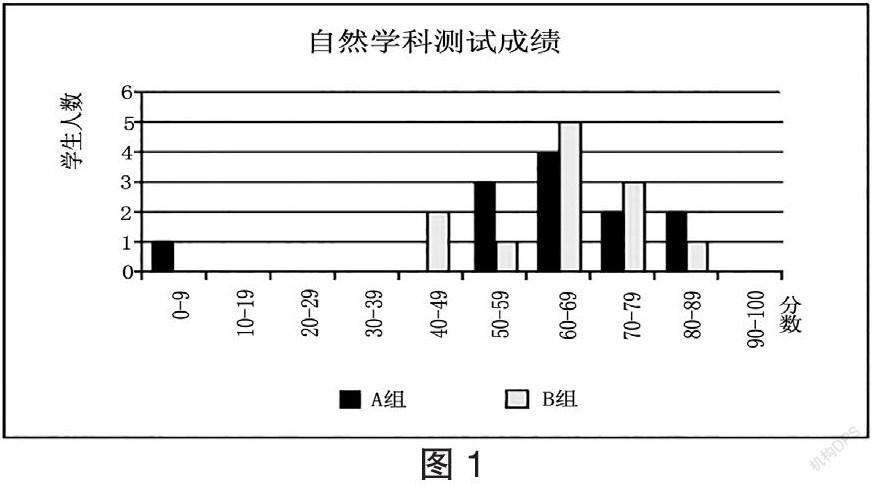
【例1】九、测试分数：图1表示了两个组在自然科学测试中的成绩，分别记为A组和B组。A组的平均分为62.0，B组的平均分64.5。超过50分则表示通过这次测试。

根据图1，老师说这次测试中B组的成绩比A组好。A组的学生不同意老师的说法，他们想尽力说服老师：B组的成绩不一定比A组好。请问：根据图1，A组的学生可以从数学上给出什么样的证据来说服老师？

【分析】本题以学生已学习经历的“测试分数成绩优异的判定”为真实情境，创设学习关联情境，命制生活实践情境试题。在对真实情境的解构中，会学是基础。根据柱状图，老师分析得出B组的平均分比A组的平均分高出2.5分，因此B组的成绩比A组好。这是对数据表面层次的解读。能用才是关键，创造性地从多角度来解构成绩，得出的结论往往不一样。因此，可以从通过测试即高于50分以上人数、高分段人数即80分以上人数、忽略最差学生的均分三个视角进行深度分析。根据柱状图，通过测试的人数，A组为11人，B组为10人，从通过人数看，显然A组成绩比B组好;80分以上，A组2个，B组1个，显然A组优秀生的人数比B组多;A组最差学生有1个在9分以下，忽略该学生，A组均分显然比B组好很多。从三个不同的视角进行分析推理，最后得出的结论都是A组比B组好。将真实问题转化为数学问题，寻找证据，进行数理运算，最后得出合理结论。

这样的生活实践情境问题解决表明，本题能够基于信息提取、知识整合、分析归纳、审辨性思维和辩证思维考查学生的证据推理、数学应用和数学探索等学科素养和创新能力，检测学生对数学知识或方法的即用能力发展水平，落实创新性考查要求。

（二）基于能想、会用真实情境，检测知用能力发展水平

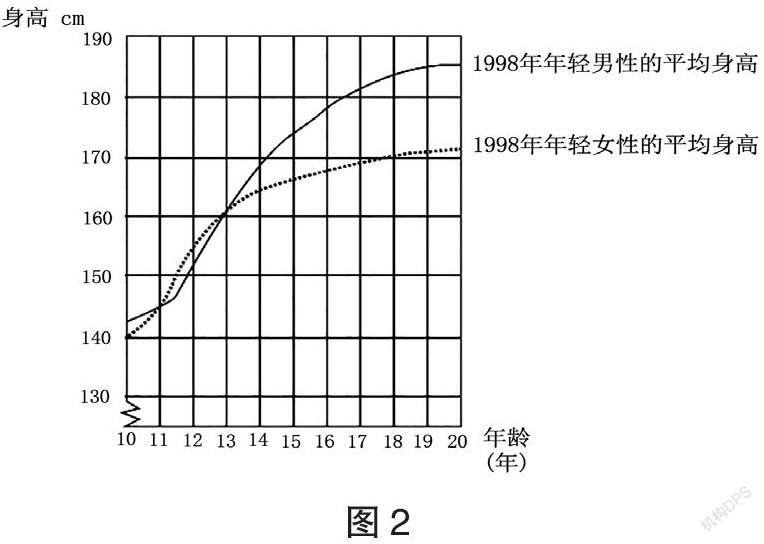
【例2】五、成长问题：年轻人长得更高——1998年荷兰年轻男性和年轻女性的平均身高如图2所示。

问题1：自从1980年以来，20岁女性的平均身高已经增长了2.3cm，达到了170.6cm。那么1980年20岁女性的平均身高是多少？

问题2：根据曲线图，在生命的哪个时期内，女性平均身高比同龄男性高？

问题3：解释曲线图是如何表示女孩在12岁以后平均成长速率逐渐降低的？

【分析】本题以成长问题“年轻人长得更高”为真实情境素材，创设学习关联情境，命制基于真实情境的试题。在真实情境问题解决过程中，能想是前提：求解“平均身高”“哪个时期”“为何逐渐降低”三个问题，分别应转化为减法问题、曲线观察分析、一次函数斜率问题不断进阶。会用是关键：第1个问题将真实问题转化为减法，即170.6-2.3=168.3（cm）;第2个问题可以转化为虚线部分高于实线部分，即女性平均身高比同龄男性高，分析曲线可知，11～13岁之间，女性平均身高高于男性;第3个问题将真实问题转化为数学问题，即函数的斜率变化问题，女性虚线部分曲线不再沿着直线上升，而是偏离直线，曲线趋于平稳，12岁以后曲线变得更平，女孩的增长曲线开始变得平坦，而男孩的增长曲线还在变大。

这样的基于真实情境的问题解决表明，本题能够基于信息提取、信息转化，多维度多视角考查学生的数学抽象、数学应用、数学推理等学科素养和数学建模、创新等关键能力，检测学生的数学知用能力发展水平，落实创新性考查要求。

（三）基于会解、优解创设真实情境，检测善用能力发展水平

会解是指学生能够根据面对问题的题设条件或求解目标的特征，建立问题与必备知识或方法之间的关系，建立解决问题所需知识或方法的思考角度，进而筛选角度解决问题;优解则是指学生能够多维度地分析所面对的问题，敏锐发现问题涉及的知识或方法之间的内在联系，化繁为简，获取问题的可能不同求解方法，同时对求解方法做出合理评估，进而优选得出求解方法。

义务教育阶段对学生数学善用能力考查的做法：精心遴选具有多维度或多样视角的真实情境素材，创设学习关联或迁移应用试题情境，命制试题，从学生会解和优解两个方面检测其数学善用能力发展水平。

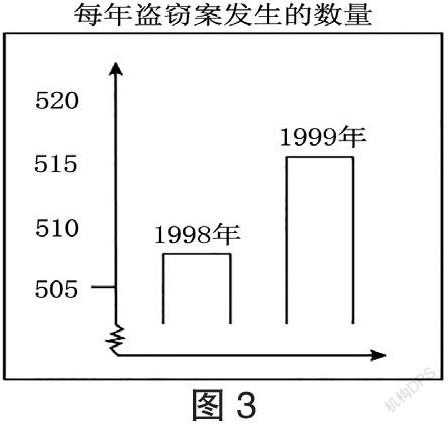
【例3】八、盗窃：一名电视台记者展示了这幅图，并且说：“这幅图显示了盗窃案件发生的数量在1998年到1999年的增长很大。”

你认为记者的表述对曲线图的解释合理吗？请给出你的理由。

【分析】本题以数据部分缺失的每年盗窃案发生的数量柱状图分析为真实情境，创设学习关联情境，命制开放性的结构不良的试题。开放性试题求解方案的多样化显而易见。会解体现为如果选择对记者的表述下的结论为不合理，需要注意到“所显示的只是图的一小部分”“论证中应用了增长速率和增长百分数”这两个分析角度;如果下的结论是不确定，则需要找到“在做出判断之前需要有一个参考依据”的分析视角。优解体现为结论如果不合理，首先最直观的表述为“应该把整个图展示出来”或“与总数500相比，10并不是一个很大的增长量”，其次可以更为详细地陈述为“只使用了图上部的一小部分，如果你观看从0到520的整幅图，你将发现增长并不是如此大”或“从百分数来看，增长大约仅为2%”，再次可以细化为“因为这个图看起来好像盗窃案增长很大，但是当你观看它们的数量时就会发现增长量并不是很大”或“这一年只增加了8或9起盗窃案，与总数507相比，这个数并不是很大”。优解体现为结论“需要有一个参考依据”，首先直接就是“我们不知道增加量是否很大，因为我们最少需要两个变化量才能比较哪个大哪个小”，其次可以表述为“我们不能判断这个增加量是否很大。如果1997年所发生的盗窃案数量与1998年相同，这时我们可以说1999年的增长量是很大的”。

本题能够基于信息提取、信息转化、知识整合、批判性思维和创新思维考查学生的数学建模、数学应用、數学探索等学科素养和创新能力，检测学生数学知识或方法的善用能力发展水平，落实创新性考查要求。

三、研究启示

义务教育阶段数学创新性考查要求的落实，要聚焦数学抽象、理性思维、数学应用、数学探索等学科素养和数学建模、创新等关键能力的考查，以真实情境和实际问题为载体，在实践中发现问题，解决问题，创新真实情境的选材思路、呈现形式和问题设计的呈现方式，从“产生多样化的想法”“产生创造性的想法”“评估和改进想法”等多维度发展学生的创新性、批判性思维，致力于学生数学知识或方法即用、知用和善用能力发展水平的检测。义务教育阶段创新性考查要求的落地实施，为“五育”并举、全面贯彻素质教育提供了很好的着力点，也有利于为基础教育阶段“评价正确导向教学”构筑支撑点。

因此，教师在日常教学过程中，要改变传统教师为主导、学生为主体的课堂结构，成为学生学习的支持者，善于提出开放性的问题，鼓励学生产生多样化的想法。教师要善于针对多样化的想法进行解剖、启发和引导，帮助学生建立从单一的视角解决数学问题进阶到多角度解决数学问题。同时，教师在引导学生产生多样化的想法之外，还要积极引导学生产生创造性的想法，让课堂真正灵动起来。要让课堂学习真正发生，就是在学生形成了高度结构化的程序解题思维之后，启发学生产生创造性的想法，让课堂的自然生成变成教学高潮的协奏曲，让创新创造成为课堂的主轴，让思维思想成为课堂的灵魂，只有创新的课堂，才会培养出具有创造性的学生。在这个过程中，教师要积极提高自己对学科的理解，加强对数学学科本质的认识，在培育学生创造性想法的过程中，不断评估和改进优化学生的想法，让学生成为有思维、有逻辑的创新性人才。

“千里之行，始于足下。”课堂改革的主战场永远在课堂，只有将创新性考查要求落实到每一节课上，未来层出不穷的创新性人才方能不断喷涌而出。

【参考文献】

中共中央，国务院.关于深化教育教学改革全面提高义务教育质量的意见 [EB/OL].[2019-07-08] （2021-08-23）.https：//baijiahao.baidu.com/s？id=1638481330270424639&wfr=spider&for=pc.