完全二部图K8,n(8≤n≤34)的点可区别E-全染色

杨 澜,陈祥恩

(西北师范大学 数学与统计学院,甘肃兰州 730070)

§1 引言

关于图的点可区别一般边染色已进行了许多研究(如[1-4]).图G的一个E-全染色φ是指使相邻点着以不同色且每条关联边与它的端点着以不同的色的全染色.用C(x)表示在φ的作用下点x的颜色以及与x关联的边的色所构成的集合(非多重集合).设φ为G的一个E-全染色,若∀u,v ∈V(G),u≠v,有C(u)≠C(v),则φ称为图G的点可区别E-全染色(Vertex-Distinguishing E-Total Coloring),简称为VDET染色.令存在k−VDET染色}.称为图G的点可区别E-全色数.

文[5]中探讨了完全图,完全二部图K2,n,星,轮,扇,路和圈的VDET染色.文[6]中得出了m个三阶圈的联图和m个四阶圈的联图的VDET色数.文[7-9]中讨论了完全二部图K3,n,K4,n,K5,n的VDET染色,文[10-11]中部分讨论了完全二部图K7,n的VDET染色.本文主要讨论了K8,n(8≤n ≤34)的VDET染色并且得到了K8,n的VDET色数.

在本文中,对于完全二部图K8,n,令V(K8,n)=X ∪Y,E(K8,n)={uivj:1≤i ≤8,1≤j ≤n},其中X={u1,u2,···,u8},Y={v1,v2,···,vn}.

给定K8,n的一个点可区别E-全染色φ,令

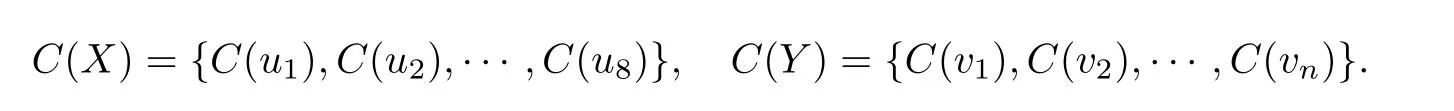
给定一个正整数k,{1,2,···,k}的i-子集是指{1,2,···,k}的包含i个元素的集合.

给定一个正整数l,一个集合M,|M|=l是指集合M中包含l个元素.

§2 主要结果及其证明

定理1当8≤n ≤34时,有(K8,n)=6.

证先证K8,n不存在5-VDET染色.设K8,n有一个5-VDET染色φ,颜色分别为1,2,3,4,5.考虑以下4种情形.

情形1|{φ(ui)|i=1,2,···,8}|=1.

此时A1中至少有3个成员都属于C(Y),可知:在2,3,4,5中至少有一种色同时包含在每个C(ui)中,不妨设2∈C(ui),i=1,2,···,8,则每个C(ui)只可能是以下8个集合之一:{1,2},{1,2,3},{1,2,4},{1,2,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},{1,2,3,4,5}.又因为{3,4},{3,5},{4,5},{3,4,5}这三个集合中至少有一个属于C(Y),则{1,2}一定不属于C(X),7个集合不能区分X中的8个顶点,矛盾.

情形2|{φ(ui)|i=1,2,···,8}|=2.

是{1,2,3,4,5}的4-子集,5-子集以及不在中的3-子集构成的集合.

情形2.1中的成员均不属于C(Y),显然也不属于C(X).

情形2.1.1Y中任一顶点的色集合不含中的成员.

事实1(i)中包含i的成员有8个,i=1,2;

事实2以下陈述中至多有一句是正确的.

(i){1,2}属于C(X);

(ii){1,3}或{2,3}属于C(X);

(iii){1,4}或{2,4}属于C(X);

(iv){1,5}或{2,5}属于C(X).

事实2的 证明假如(i)-(iv)中至少有两条是正确的,鉴于(ii),(iii),(iv)的地位是等价的,故只考虑以下两种情况.若(i)和(ii)正确,此时C(Y)中的每个成员同时包含1,3(或2,3),由事实1(iv)知,只有6个集合可以作为C(X)中的成员,矛盾;若(ii)和(iii)正确,此时C(Y)中的每个成员同时包含3,4,由事实1(v)知,只有7个集合可以作为C(X)中的成员,矛盾.事实2证毕.

事实3出现在事实2中的四条陈述都不正确.

事实3的证明假如(i)成立,由1和2的对称性,不妨设其顶点颜色为2,则每个C(vj)包含颜色1,故C(X)∪C(Y)1,2}}{{3,4,5}},其中1,2}}{{3,4,5}}包含16个成员.再由C(Y)中的成员均不是中的,也不是{1,2},且每个C(vj)均包含颜色1,可知:C(Y)⊆{{1,3,4},{1,3,5},{1,4,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},{1,3,4, 5},{1,2,3,4,5}},故C(X)⊆{{1,2},{1,2,3},{1,2,4},{1,2,5},{2, 3, 4},{2, 3, 5},{2, 4, 5},{2,3, 4, 5}}.现由{1,4,5}属于C(Y),若其顶点颜色为4,则{2,3,4}不能与之染色成功,矛盾;若其顶点颜色为5,则{2,3,5}不能与之染色成功,矛盾.因此(i)不成立.

假如(ii)成立,则C(Y)的每个成员均包含颜色3.由假设及事实1(ii)知,C(Y)只可能是中10个含3的成员.此时考虑8≤n ≤10的情况,可知C(X)∪C(Y)1,3},{2,3}},其中1,3},{2,3}}包含18个成员.此时以下两个断言是正确的.

断言1{1,3,4}和{1,3,5}至多有一个属于C(Y).

断言1的证明假如{1,3,4}和{1,3,5}均属于C(Y),由于{1,3}或{2,3}属于C(X),其顶点颜色为1或2,其关联边颜色为3,故{1,3,4}和{1,3,5}的顶点颜色只能是4和5,其关联边的颜色只能是1或3.于是{1,4,5}和{2,4,5}均不属于C(X).再由C(Y)中的每个成员均包含颜色3,则{1,4,5}和{2,4,5}均不属于C(Y),此时

其中1,3},{2,3}}{{1,4,5},{2,4,5}}包含16个成员.下面考虑n=8的情况.由于C(X)中的每个成员均包含1或2,故{3,4,5}属于C(Y),且其顶点颜色不是3.若其顶点颜色为4,则{1,2,4}不能与之染色成功,矛盾;若其顶点颜色为5,则{1,2,5}不能与之染色成功,矛盾.断言1证毕.

断言2{2,3,4}和{2,3,5}至多有一个属于C(Y).

断言2的证明与断言1类似,此处不再赘述.

根据断言1和断言2,由对称性,可不妨设{1,3,4}和{2,3,5}属于C(Y),其顶点颜色分别为4和5,则{1,4,5},{2,4,5}和{1,2,4,5}均不属于C(X),否则与E-全染色矛盾,并且{1,4,5},{2,4,5}和{1,2,4,5}也不属于C(Y).此时

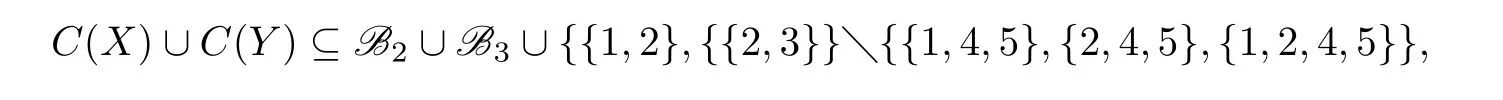
15个集合不能区分X和Y中的至少16个顶点,矛盾.因此(ii)不成立.

至于(iii)或(iv)可类似(ii)推出矛盾.

至此,事实3证毕.

以上事实说明:含1或2的2-子集均不属于C(X),从而C(X)∪C(Y)⊆B2∪B3,B2∪B3恰好包含16个集合.由前面的推理知:{3,4,5}属于C(Y),中的成员都属于C(X).若{3,4,5}的顶点颜色为3,则与{1,2,3}染色不成功,矛盾;若{3,4,5}的顶点颜色为4,则与{1,2,4}染色不成功,矛盾;若{3,4,5}的顶点颜色为5,则与{1,2,5}染色不成功,矛盾.

情形2.1.2中至少有一个成员属于C(Y).

不妨设为{1,2,3},则C(X)中的每个成员将同时包含颜色1和颜色2,因此只有以下7个集合可以作为X中的顶点的色集合：{1,2},{1,2,4},{1,2,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},{1,2,3,4,5},7个集合不能区分X中的8个顶点,矛盾.

情形2.2中至少有一个成员属于C(Y).

此时每个C(ui),i=1,2,···,8至少同时包含3,4,5中的某一种色,不妨设3∈C(ui),i=1,2,···,8.

情形2.2.1中的成员均不属于C(Y),显然{1,2,4}和{1,2,5}不是X和Y中任一顶点的色集合.下面分情况讨论.

(i){1,3}和{2,3}中至少有一个属于C(X).

此时C(Y)中的每个成员都包含颜色3,从而C(X)和C(Y)中的每个成员都包含颜色3,因此C(X)∪C(Y)1,3},{2,3}}{{4,5},{1,2,4},{1,2,5},{1,4,5},{2,4,5},{1,2,4,5}},即8+n ≤19+2−6=15,15个集合不能区分X和Y中的至少16个顶点,矛盾.

(ii){1,3}和{2,3}都不属于C(X).

由{1,2,4}和{1,2,5}不是X和Y中任一顶点的色集合,可知

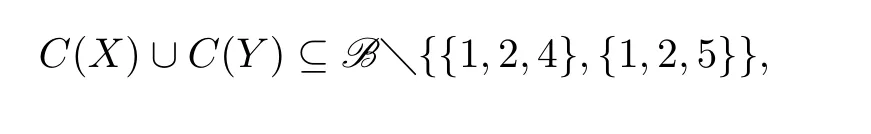
下面分情况讨论.

若{1,2,3}属于C(X),则{4,5}不属于C(Y),显然也不包含于C(X).此时C(X)∪C(Y)1,2,4},{1,2,5},{4,5}},有8+n ≤19−3=16.下面只考虑n=8的情形.由C(Y)中的每个成员均包含颜色3,故{1,4,5}和{2,4,5}不属于C(Y),则它们属于C(X).如果{1,2,3}的顶点颜色为1,那么{1,4,5}不能与之染色成功,矛盾;如果{1,2,3}的顶点颜色为2,那么{2,4,5}不能与之染色成功,矛盾.

若{1,2,3}不属于C(X),则中的成员均不是X和Y中任一顶点的色集合,此时C(X)∪C(Y),有8+n ≤19−3=16.下面只考虑n=8的情形.由前面的推理知:中的成员均属于C(Y),且每个C(ui)至少同时包含3,4,5中的某两种色.由对称性,不妨设每个C(ui)包含3,4,则C(X)只能是以下6个集合之一：{1,3,4},{2,3,4},{1,2,3,4},{1,3,4,5},{2,3,4,5},{1,2,3,4,5},矛盾.

情形2.2.2中至少有一个成员属于C(Y).

此时{1,2} ∈C(ui),i=1,2,···,8,从而C(X)中的成员只能是以下4个集合之一：{1,2,3},{1,2,3,4},{1,2,3,5},{1,2,3,4,5},矛盾.

情形3|{φ(ui)|i=1,2,···,8}|=3.

不妨设φ(ui)∈{1,2,3},i=1,2,···,8,则当C(vj)是2-子集时不包含颜色1,不包含颜色2,也不包含颜色3,是3-子集时不是{1,2,3},因此可以作为Y中顶点色集合的{1,2,3,4,5}的子集的数目为.当17≤n ≤34时,矛盾.下面考虑8≤n ≤16的情况.令,其中

为{1,2,3,4,5}的4-子集,5-子集以及不在1,2,3}}中的3-子集构成的集合.

情形3.1{4,5}属于C(Y).

此时C(X)中的每个成员同时包含颜色4或颜色5,由4和5的对称性,不妨设为4.下面分情况讨论.

情形3.1.1{1,4},{2,4},{3,4}中至少有一个包含于C(X).

此时C(Y)中的每个成员均包含颜色4,从而{1,2,5},{1, 3, 5},{2,3,5}和{1,2,3,5}都不属于C(Y),显然也不属于C(X),故C(X)∪C(Y)⊆C ∪{{1,4},{2, 4},{3,4}}{{1,2,5},{1,3,5},{2,3,5},{1,2,3,5}},即8+n ≤16+3−4=15,15个集合不能区分X和Y中的至少16个顶点,矛盾.

情形3.1.2{1,4},{2,4}和{3,4}都不属于C(X).

此时C(X)∪C(Y),而恰好包含16个集合,下面仅考虑n=8的情况.由于C(X)中每个成员同时包含颜色4,故{1,2,5},{1,3,5}和{2,3,5}都不属于C(X),从而只能属于C(Y),则C(X)中的每个成员同时包含颜色1,颜色2和颜色3,因此C(X)中的成员只能是以下2个集合：{1,2,3,4},{1,2,3,4,5},矛盾.

情形3.2{4,5}不属于C(Y),显然也不属于C(X),则C(Y).

事实5以下陈述中至多有一句是正确的.

(i){1,2},{1,3}和{2,3}中至少有一个属于C(X);

(ii){1,4},{2,4}和{3,4}中至少有一个属于C(X);

(iii){1,5},{2,5}和{3,5}中至少有一个属于C(X).

事实5的证明假如(i)-(iii)中至少有两条是正确的,鉴于(ii)和(iii)的地位是等价的,故只考虑以下两种情况.若(i)和(ii)正确,此时C(Y)中的每个成员至少同时包含1,4(或2,4,或3,4),由事实4(iv)知,只有7个集合可以作为C(X)中的成员,矛盾;若(ii)和(iii)正确,此时C(Y)中的每个成员同时包含4和5,由事实4(v)知,只有7个集合可以作为C(X)中的成员,矛盾.事实5证毕.

事实6出现在事实5中的三条陈述都不正确.

事实6的证明当(i)成立时,C(Y)中的每个成员至少同时包含1,2,3中的某一种色,由于1,2,3的对称性,不妨设为1,则可以作为C(Y)中的成员的只能从中选取,其中={{1,2,4},{1,2,5},{1,3,4},{1,3,5},{1,4,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},{1,3,4,5},{1,2,3,4,5}},且||=10.因此中至多有两个成员不属于C(Y),即{1,2,4},{1,2,5},{1,3,4}和{1,3,5}中至少有2个成员属于C(Y).此时以下断言是成立的:

断言3{1,2,4},{1,2,5},{1,3,4}和{1,3,5}中恰有2个属于C(Y).

断言3的证明如果{1,2,4},{1,2,5},{1,3,4}和{1,3,5}中至少有3个属于C(Y),则{2,4,5},{3,4,5},{2,3,4},{2,3,5},{2,3,4,5}均不属于C(X),显然也不属于C(Y),此时C(X)∪C(Y)1,2},{1,3},{2,3},{1,2,3}}{{2,4,5},{3,4,5},{2,3,4},{2,3,5},{2,3,4,5}},即8+n ≤15+4−5=14,14个集合不能区分X和Y中的至少16个顶点,矛盾.断言3证毕.

根据断言3,继续分以下情况进行讨论.

若{1,2,4}和{1,2,5}属于C(Y),{1,3,4}和{1,3,5}不属于C(Y),即

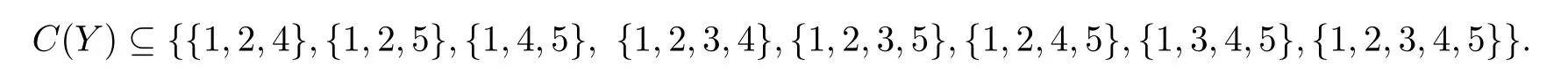
由于{2,4,5},{3,4,5}不能与{1,2,4},{1,2,5}染色成功,故{2,4,5}和{3,4,5}均不属于C(X).又因为{1,4,5}属于C(Y),则{2,3}不属于C(X),此时

如果{1,4,5}的顶点颜色为4,则{2,3,4}与之染色不成功,矛盾;如果{1,4,5}的顶点颜色为5,则{2,3,5}与之染色不成功,矛盾.

若{1,2,4}和{1,3,4}属于C(Y),{1,2,5}和{1,3,5}不属于C(Y),即

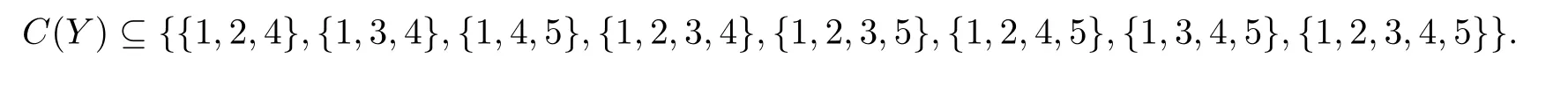
由于{2,4,5},{3,4,5},{2,3,4,5}不能与{1, 2,4},{1,3,4}染色成功,故

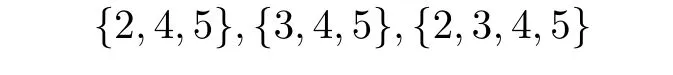
均不属于C(X).又由{1,4,5}属于C(Y),由4,5的对称性,不妨设顶点颜色为5,则{2,3}和{2,3,5}都不属于C(X),此时C(X)⊆{{1,2},{1,3},{1,2,3},{2,3,4},{1,2,5},{1,3,5}},6个集合不能区分X中的8个顶点,矛盾.

综上(i)不成立.

当(ii)成立时,此时{1,2,4},{1,3,4},{2,3,4}和{1,2,3,4}都不是Y中任一点的色集合,因此

7个集合不能区分Y中的至少8个顶点,矛盾.因此(ii)不成立.

至于(iii)可类似(ii)推出矛盾.

至此事实6证毕.

以上事实说明:含1的2-子集,含2的2-子集,含3的2-子集均不属于C(X),从而

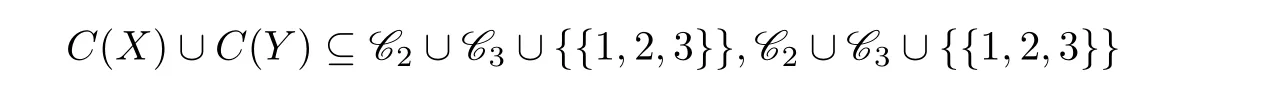
恰好包含16个成员.因此{1,2,3}必为X中某个顶点的色集合,由1,2,3的对称性,不妨设顶点颜色为1,则{1,4,5}不能与之染色成功.因此{1,4,5}不属于C(Y),从而属于C(X).以下分情况讨论.

如果中的成员均不属于C(Y),则必然属于C(X),此时C(X)⊆{{1,2,3},{1,4,5},{1,2,4},{1,2,5},{1,3,4},{1,3,5},{2,3, 4},{2,3,5}},从而

C(Y)⊆{{2,4,5},{3,4,5},{1,2,3,4},{1,2,3,5},{1,2,4,5},{1, 3,4,5},{2,3,4,5},{1,2,3,4,5}}.但{2,4,5}与{1,3,5}染色不成功,矛盾.

如果中的成员至少有一个属于C(Y),不妨设为{1,2,4},则{1,4,5}不能与之染色成功,即{1,4,5}不属于C(X),显然{1,4,5}不是X和Y中任一顶点的色集合.此时

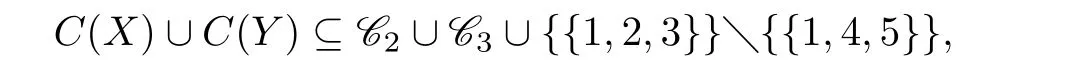
即8+n ≤15+1−1=15,15个集合不能区分X和Y的至少16个顶点,矛盾.

情形4.

不妨设φ(ui)∈{1,2,3,4},i=1,2,···,8,则每个C(vj)均不是2-子集,是3-子集时不是{1,2,3},{1,2,4},{1,3,4},{2,3,4},是4-子集时不是{1,2,3,4},因此可以作为Y中顶点色集合的{1,2,3,4,5}的子集的数目为

当12≤n ≤34时,11个集合不能区分Y中的n个顶点,矛盾.以下仅考虑8≤n ≤11 的情况.令=,其中

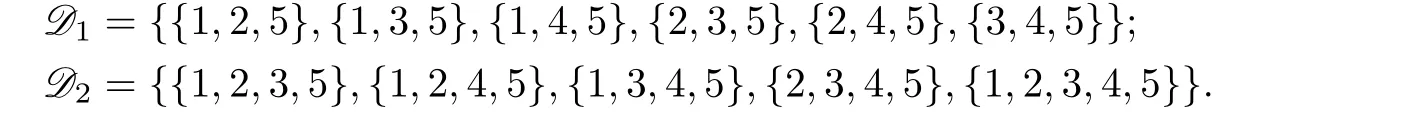
经计算得中包含i的成员有7个,i=1,2,3,4;D中包含5的成员有11个.因此{1,2},{1,3},{1,4},{2,3},{2,4},{3,4}均不属于C(X).

情形4.1{1,5},{2,5},{3,5},{4,5}均不属于C(X).

此时C(X)∪C(Y),其中

且||=16.显然中的成员均是C(X)中的成员,故中恰有3个是C(X)中的成员.由1,2,3,4的对称性,可设{1,2,5},{1,3,5},{1,4,5}属于C(X),则{2,3,5},{2,4,5},{3,4,5}必然属于C(Y),与VDET染色矛盾.

情形4.2{1,5},{2,5},{3,5},{4,5}中至少有一个属于C(X).

此时中的元素均不属于C(Y),且有C(Y),而||=5,5个集合不能区分Y中的至少8个顶点,矛盾.

因此,K8,n(8≤n ≤34)不存在5-VDET染色,即当8≤n ≤34时,.下面给出K8,n的一个6-VDET染色.

首先在表1中给出了φ34(表1的第一行表示顶点ui(1≤i ≤8)的色集合,第二行表示顶点ui(1≤i ≤8)的颜色,第三行的34(4)表示顶点v1着色4,v1的关联边u1v1,···,u8v1分别着色3,3,3,3,3,3,3,3,3,3,以下如此类推).当8≤j ≤34时,K8,34的6-VDET染色φ34在由所导出的子图上的限制显然是K8,j的6-VDET染色φj.

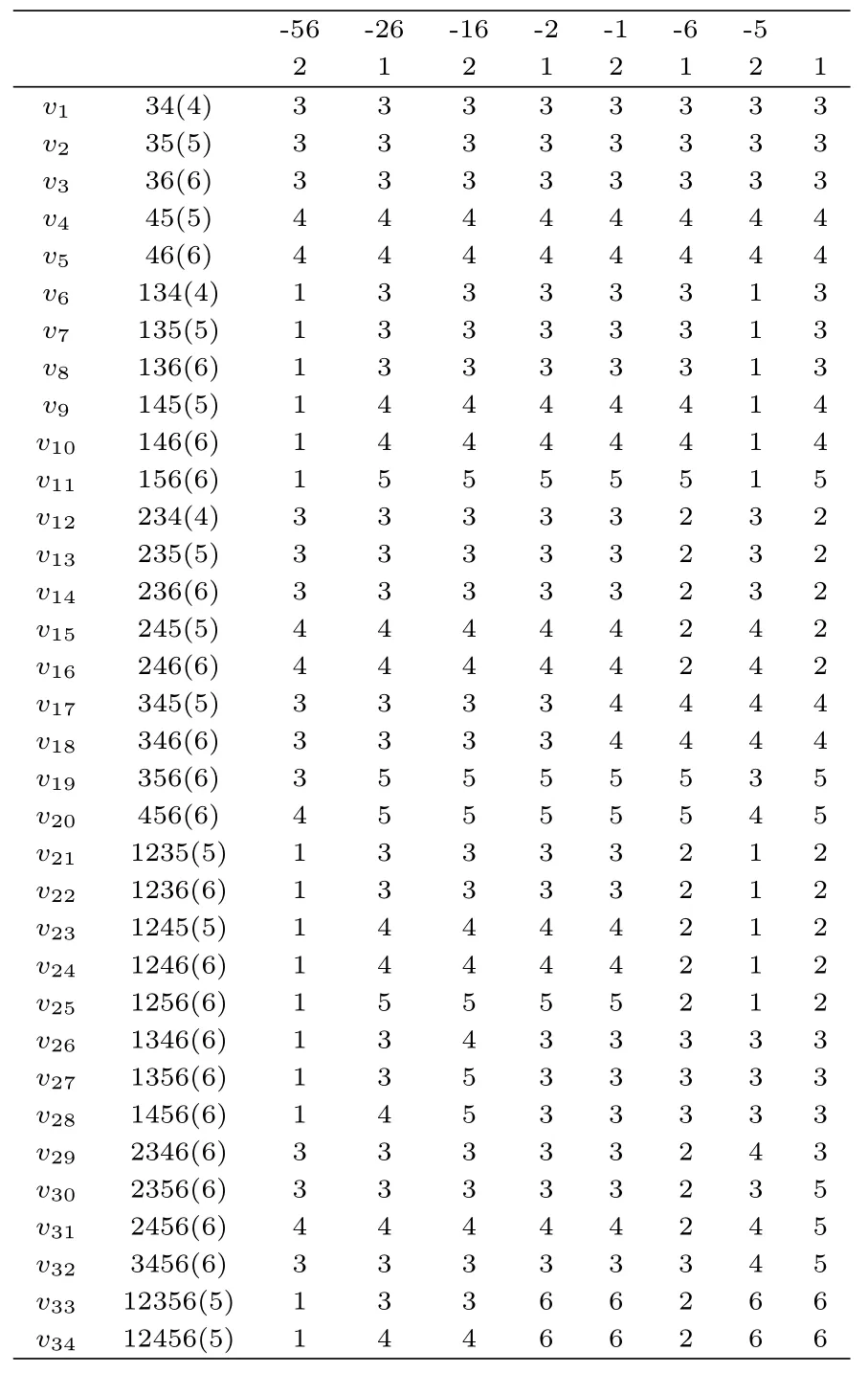
表1 K8,34 的6-VDET 染色φ34

当n ≥35时,将对K8,n的VDET色数继续进行研究.