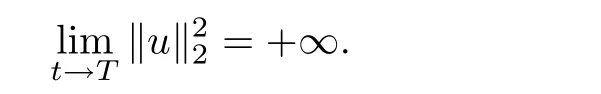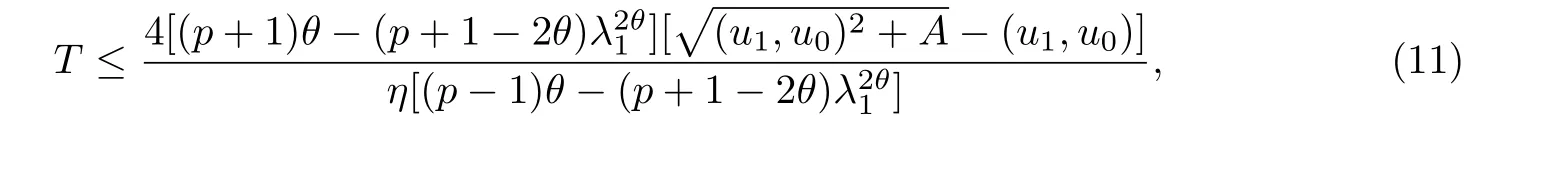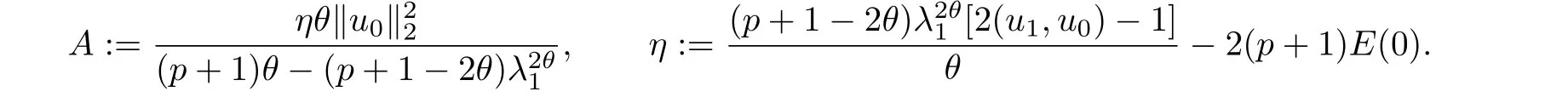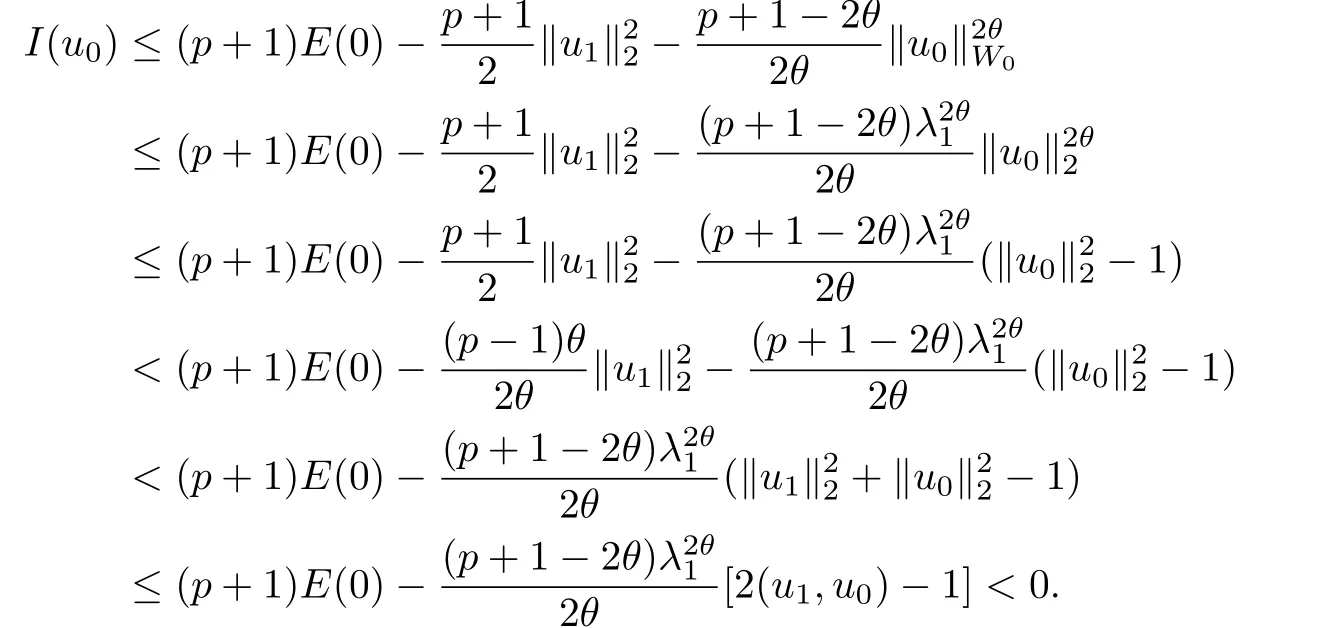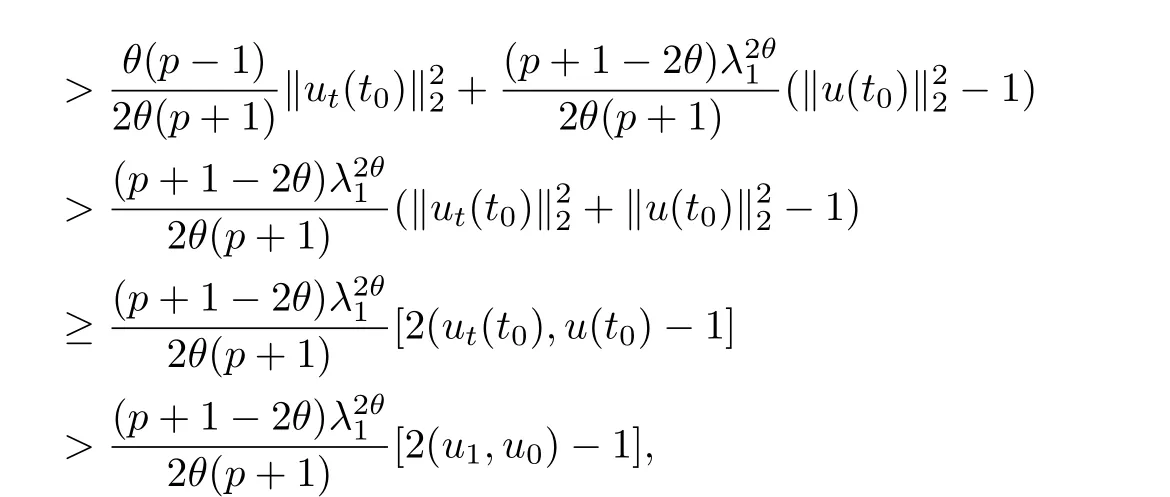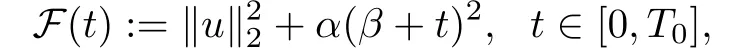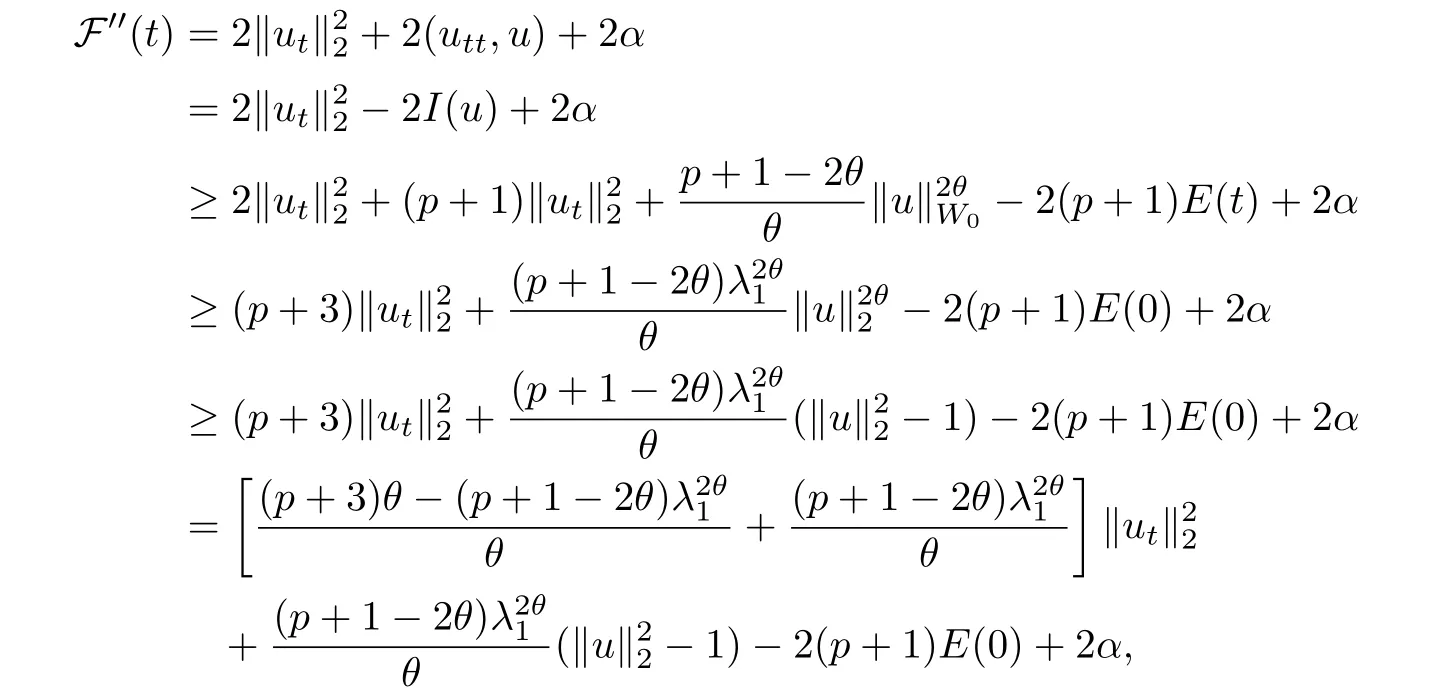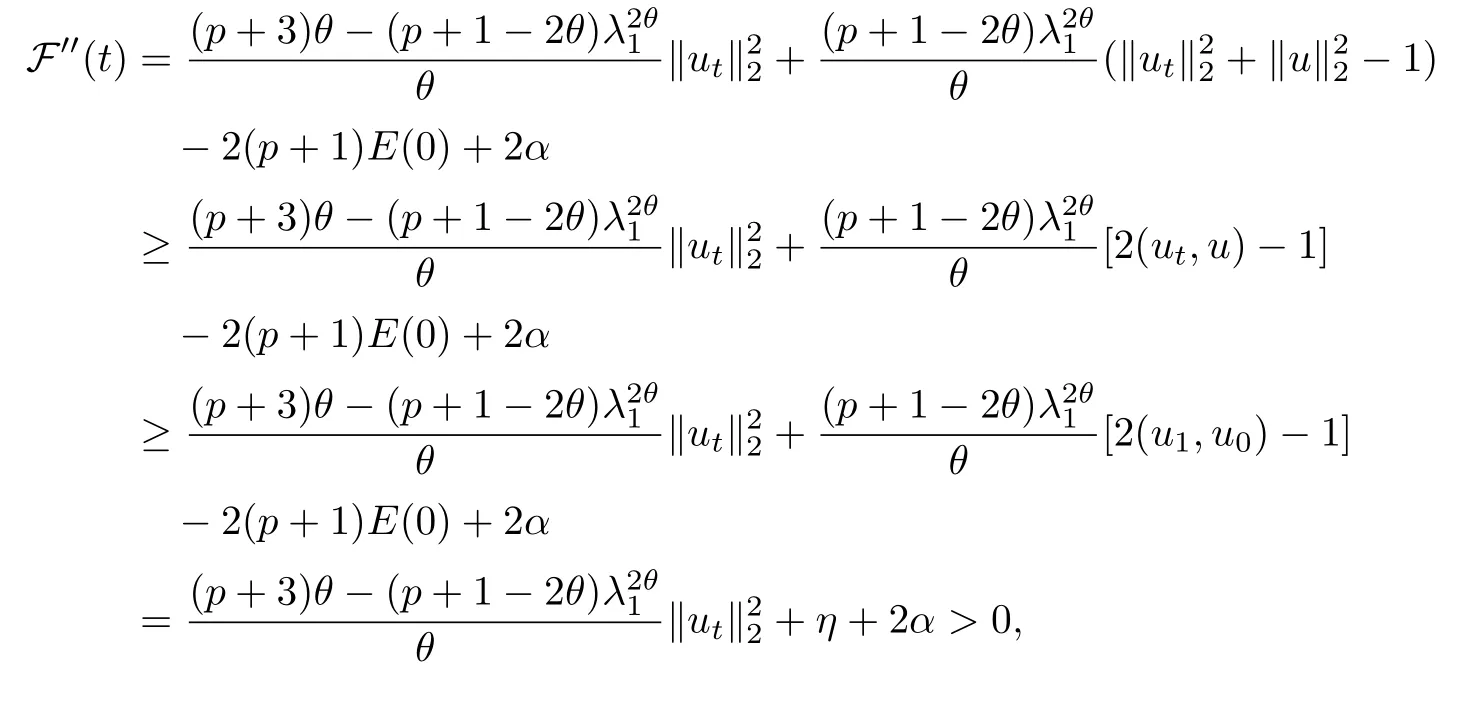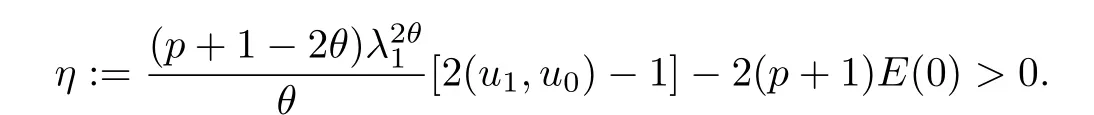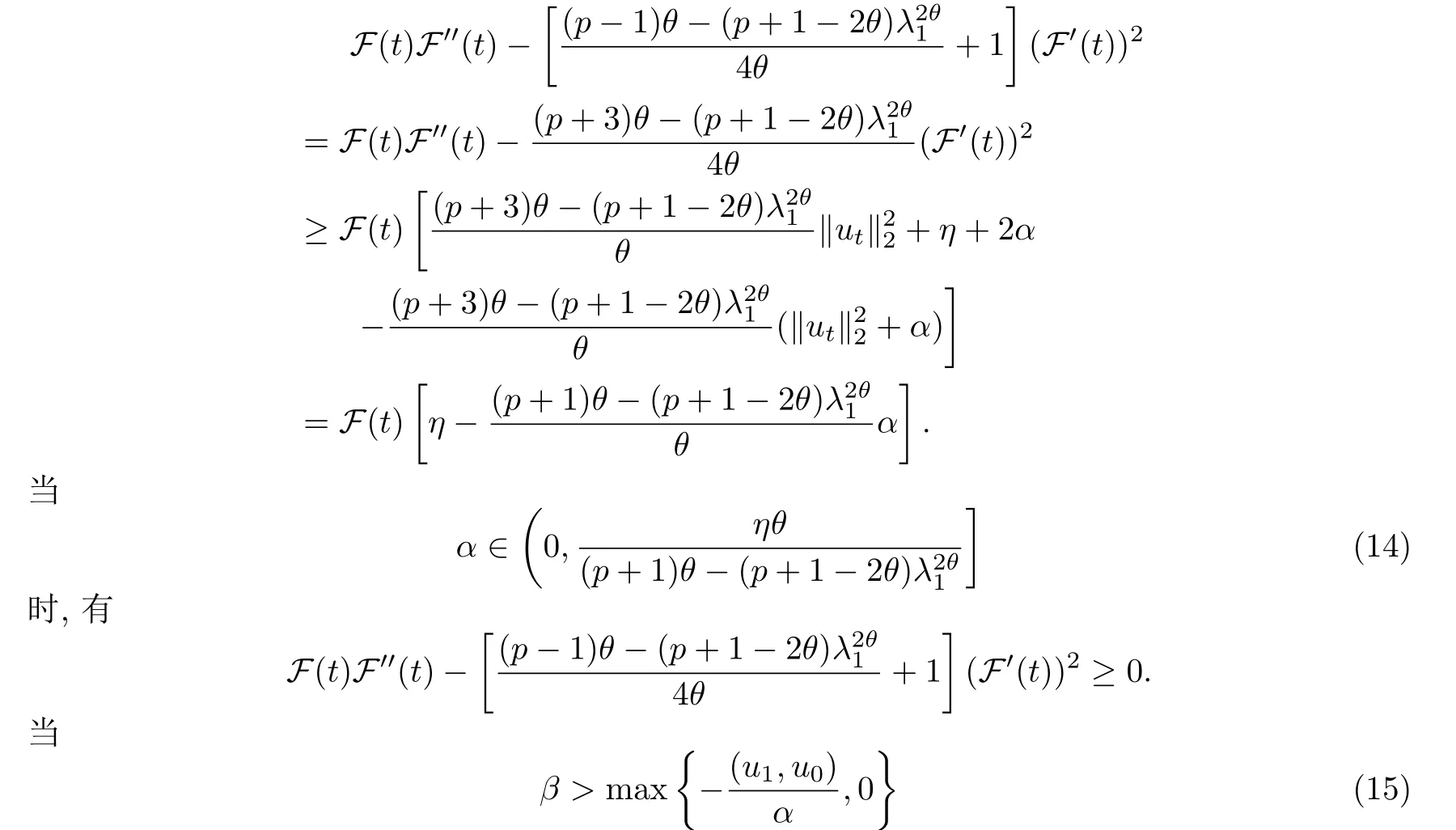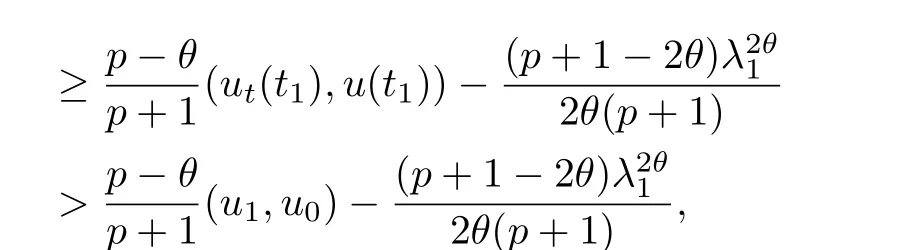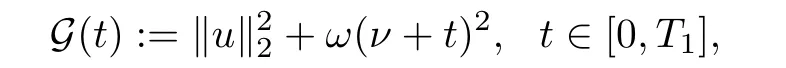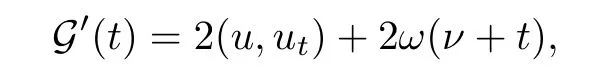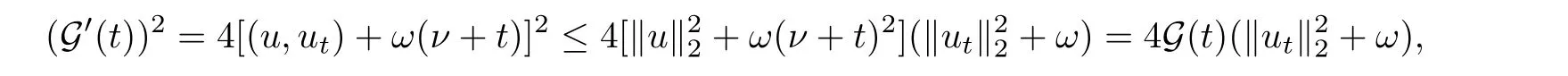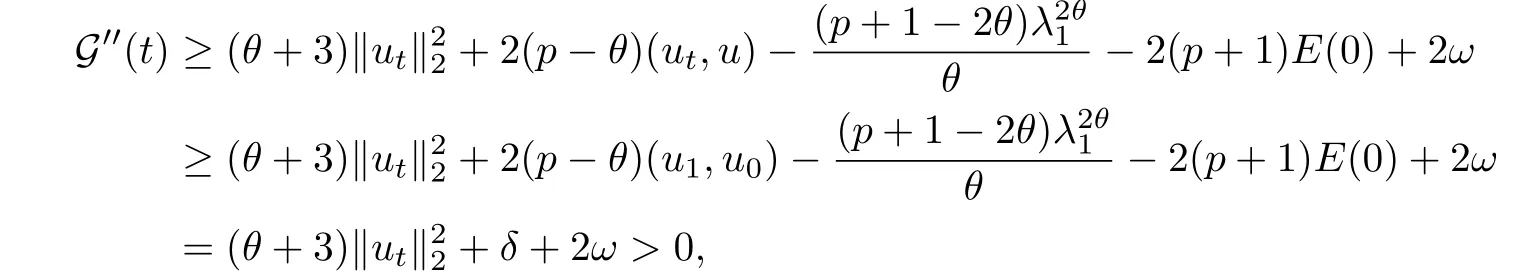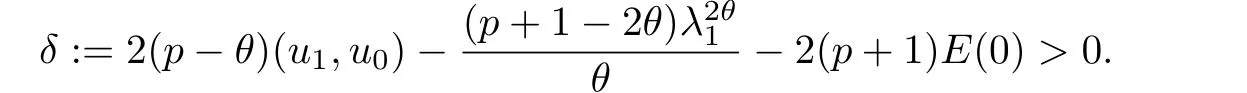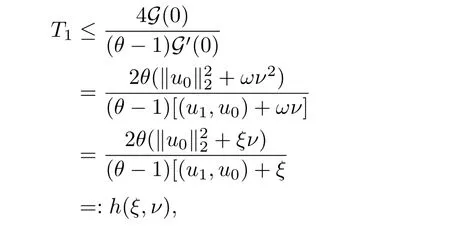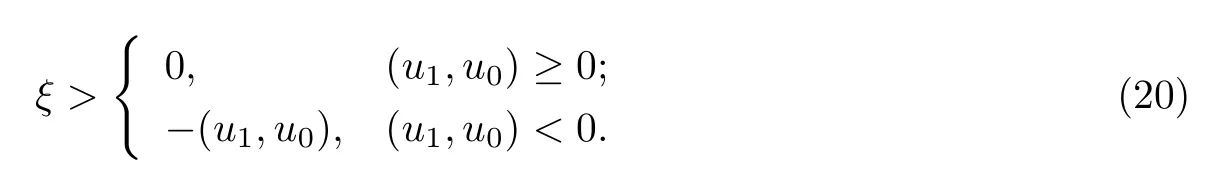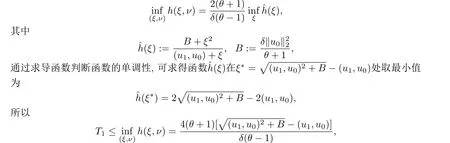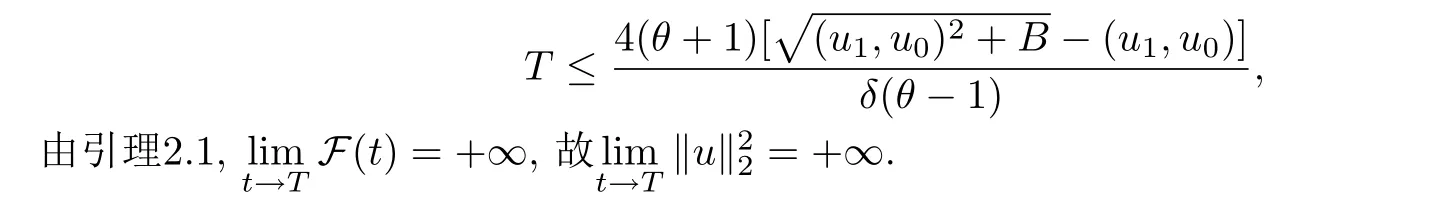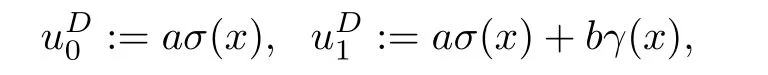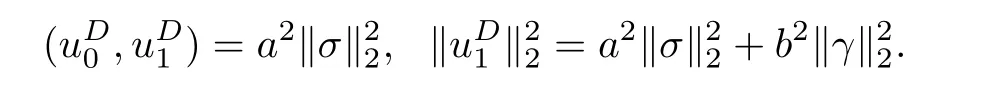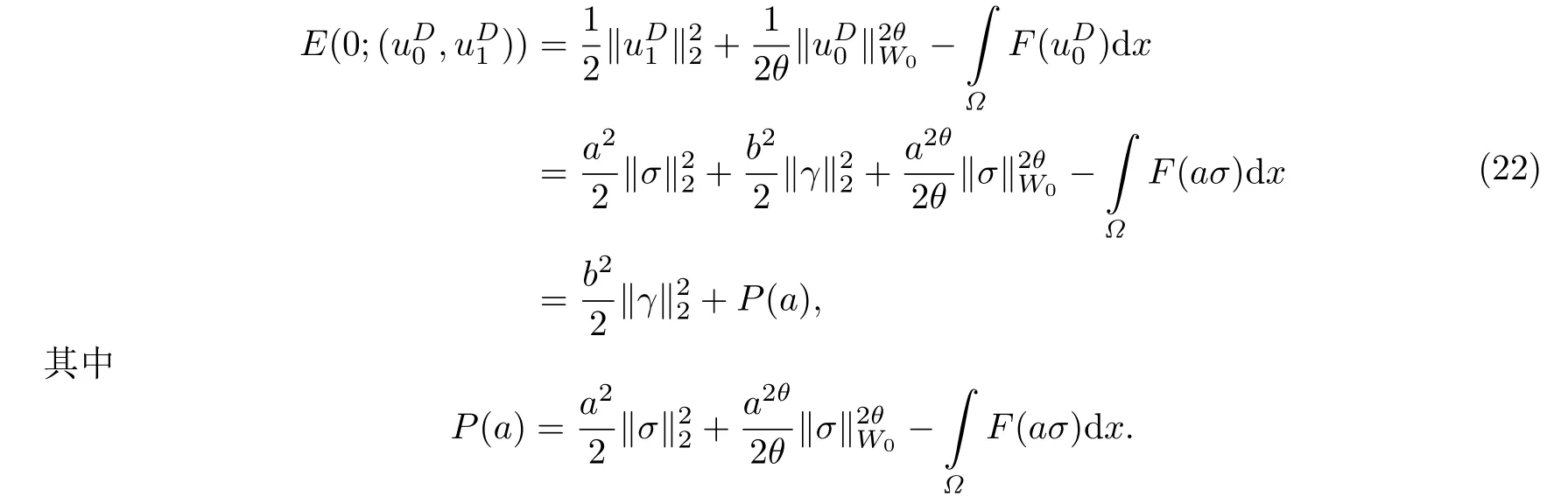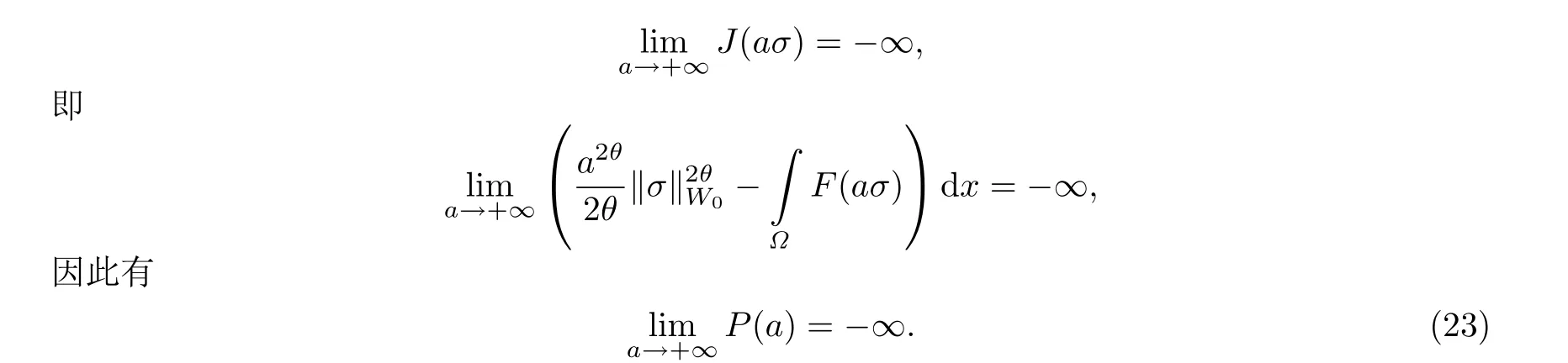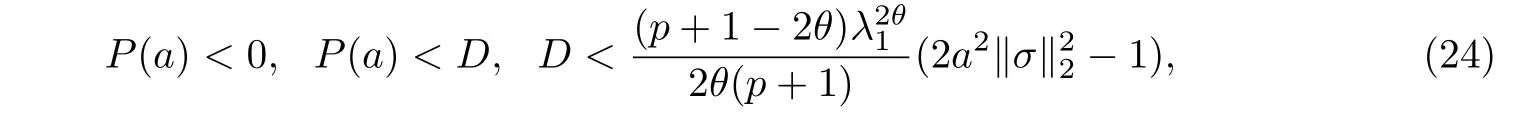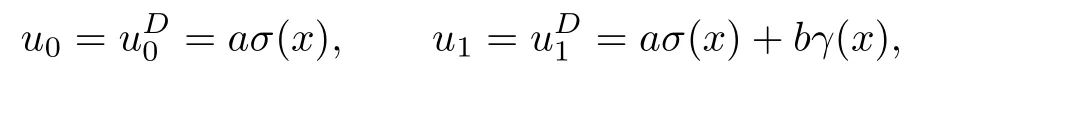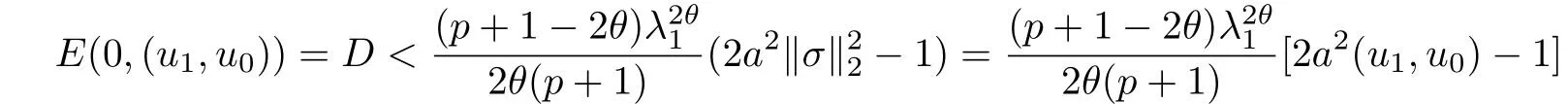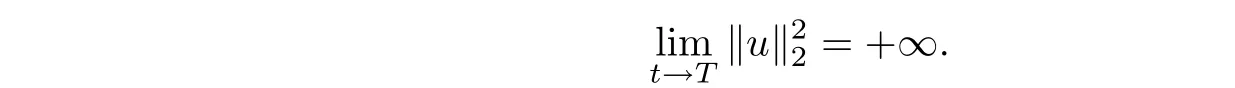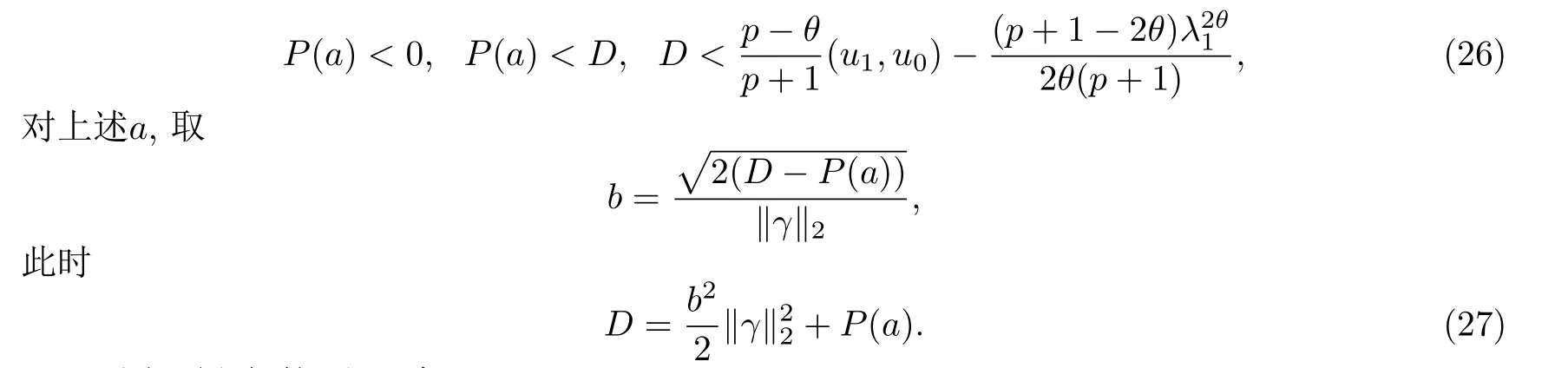一类Kirchhoff型双曲方程在任意初始能量下的有限时刻爆破
2021-12-28邵湘琨唐国吉
邵湘琨 唐国吉
(1.广西民族大学 数学与物理学院,广西南宁 530006;2.广西混杂计算与集成电路设计分析重点实验室,广西南宁 530006)
§1 引言
本文主要考虑如下带有分数次算子的Kirchhoff型双曲方程的初边值问题
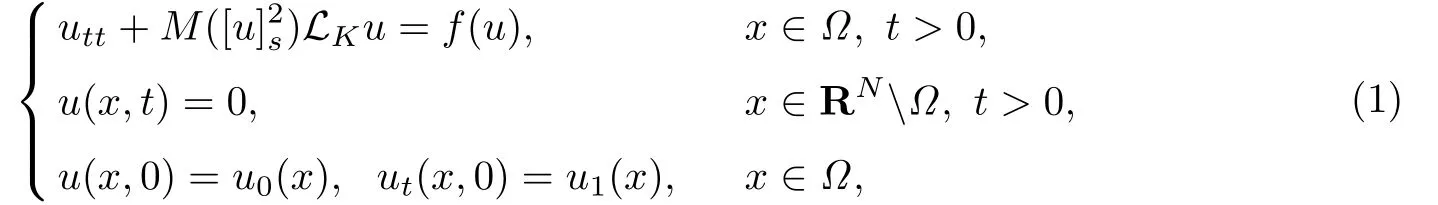
其中Ω ⊂RN是一个具有Lipschitz边界的有界区域,0 这里Bε(x)表示以x ∈RN为中心,ε>0为半径的球,函数K:RN {0}→(0,+∞) 满足 (k1)wK ∈L1(RN),其中w(x)=min{1,|x|2}; (k2) 存在正常数K0,使得对任意x ∈RN {0},都有K(x)≥K0|x|−N−2s. Kirchhoff函数M满足 (M0) 对任意的t ∈[0,+∞)和有M(t):=tθ−1,其中 此外,假设函数f:R→R满足 (S1)f ∈C1(R),f(0)=f′(0)=0,并且在原点附近有f/≡0; (S2) 满足下面的(a)或(b); (a)f(u)在R上是单调的,且在(0,+∞)上是凸函数,在(−∞,0)上是凹函数; (b)f(u)在R上是凸函数; 近几十年来,分数次Kirchhoff型方程受到国内外专家学者的广泛研究(见[1-7]及其参考文献),它可以描绘大量的自然现象,能够作为大气流体力学,金融经济学等诸多实际问题中的模型,在解的性质方面也得到了许多很好的成果,比如方程解的存在性,渐进性和爆破性质(详见[8-11]及其参考文献)等. 特别地,当Kirchhoff函数M满足假设(M0)并且f满足假设(S1)-(S4)时,问题(1)已经在文献[12]中被研究,通过应用Galerkin方法以及势阱法(参见[13]),Pan-Pucci-Zhang讨论了问题解的真空隔离现象,得到了解在低初始能量和临界初始能量下的全局存在性以及低初始能量时的有限时刻爆破性质.一个自然的问题是:问题(1)的解是否在任意高初始能量下有限时刻爆破呢?这是本文研究的主要动机. 本文找到了一个与势阱深度无关的有限时刻爆破条件,进一步利用此爆破条件得到了问题(1)的解在任意高初始能量时的有限时刻爆破结果.此工作进一步扩展了文献[12]中得到的爆破结果. 本文余下部分这样安排:§2给出一些预备知识,并列出一些重要的引理;§3给出本文的主要结果. 在这一节,先回顾分数次Sobolev空间的一些定义和性质(见[12]).用(·,·)表示空间L2(Ω)的内积,用‖·‖p表示空间Lp(Ω),p ∈[1,+∞]的范数. 设W是由Lebesgue可测函数u:RN→R 构成的线性空间,并且满足u ∈L2(Ω)和−u(y)|2K(x −y)dxdy <+∞,其中Q=R2N (C(Ω)×C(Ω)),C(Ω)=RN Ω.其范数定义为 接着定义线性闭子空间W0={u ∈W:u(x)=0在RN Ω上几乎处处成立},其范数与(2)等价(见[14]), 由条件(k1)和[15,引理6]可知,空间W0连续嵌入到空间Lq(Ω),q ∈[1,],因此对任意的u ∈W0和q ∈[1,],存在正常数Cq,使得‖u‖q ≤Cq‖u‖W0. 考虑关于算子LK的特征值问题(见[9]) 定义上述问题的第一特征值λ1为 进一步可以得到 接着,由[12],以下回顾一系列泛函. 问题(1)的能量泛函为 势阱能量泛函为 对应的Nehari泛函为 问题(1)的弱解定义如下. 定义2.1如果函数u(x,t)满足u ∈L∞(0,∞;W0),ut ∈L∞(0,∞;L2(Ω)),且 其中u(x,0)=u0∈W0,ut(x,0)=u1∈L2(Ω),T为解的最大存在时间,那么就称u=u(x,t)是问题(1)的弱解. 下面这个引理(见[16-17])主要用于方程的解在有限时刻爆破的证明,而且可以用于估计爆破时间的上界. 引理2.1设0 其中ζ是个正常数.如果M(0)>0,M′(0)>0,那么limt→T M(t)=+∞,而且 下面给出了关于方程组(1)的能量不等式(见[12]). 引理2.2假设(M0)成立,f满足(S1)-(S4),T为解u的最大存在时间,则有 除此之外,回顾[12,引理3.3]如下. 引理2.3假设(M0)成立,f满足(S1)-(S4),u ∈W0,u≠0,ϑ是非负实数,则有 下面给出I和E的一个关系式. 引理2.4假设(M0)成立,f满足(S1)-(S4),u是问题(1)的弱解,则有 证利用(6),(5),(4)及假设(S4),简单证明如下. 本节给出本文的主要结果.设u(x,t),t ∈[0,T)是问题(1)的弱解. 定理3.1假设(M0)成立,f满足(S1)-(S4),u0∈W0,如果 那么问题(1)的弱解u在有限时刻T爆破,即 另外,若(i)成立,则有爆破时间T的上界估计 其中 若(ii)成立,则有爆破时间T的上界估计 设函数V(t):=(ut,u),t ∈[0,T),则由I(u)的定义得 下面把证明过程分为两种情况进行讨论. 情况1(p −1)θ >(p+1−2θ),初始能量E(0) 满足(9). 首先证明对任意的t ∈[0,T),都有I(u)<0和(ut,u)≥(u1,u0).依次利用引理2.4,(2),(13),Schwarz不等式和条件(9)可得到I(u0)<0,详细过程如下. 假如I(u)<0,∀t ∈[0,T)不成立,那么一定存在一个时刻t0∈(0,T),使得I(u(t0))=0且在[0,t0)有I(u)<0,那么对于∀t ∈[0,t0)有V′(t)>0,即V(t) 在[0,t0)单调递增,故(u1,u0)<(ut(t0),u(t0)). 由能量不等式(8),I(u(t0))=0,引理2.4,(2),(13),Schwarz不等式,(u1,u0)<(ut(t0),u(t0)),有 这与(9)矛盾.因此I(u)<0,∀t ∈[0,T)成立.从而,V(t)在[0,T) 单调递增,即(ut,u)≥(u1,u0),∀t ∈[0,T). 接下来证明问题(1)解的有限时刻爆破性质,并估计爆破时间的上界.对于任意的T0∈(0,T),定义如下函数 其中α,β为正常数.容易算得F′(t)=2(u,ut)+2α(β+t),再用Schwarz不等式,可以得到 依次利用I(u)的定义,引理2.4,(2),(8),(13),有 再结合Schwarz不等式以及(ut,u)≥(u1,u0),∀t ∈[0,T),可以得到 其中由(9)可知 把上述关于(F′(t))2和F′′(t)的结果代入下式,很容易得到 时,有F′(0)>0.进一步,由引理2.1可得 其中φ:=αβ,又由(15)可得到 由(14)可得 现在求g(φ,β)的下确界,其中φ满足(16),β满足(17),则 类似于情况1.首先证明对任意的t ∈[0,T),都有I(u)<0和(ut,u)≥(u1,u0).使用引理2.4,(2),(13),Schwarz不等式和(10)可得到I(u0)<0,详细过程如下. 假如I(u)<0,∀t ∈[0,T)不成立,那么一定存在一个时刻t1∈(0,T),使得I(u(t1))=0且在[0,t1)有I(u)<0,那么对于∀t ∈[0,t1)有V′(t)>0,即V(t)在[0,t1)单调递增,故(u1,u0)<(ut(t1),u(t1)). 根据(8),I(u(t1))=0,引理2.4,(2),(13),Schwarz不等式,(u1,u0)<(ut(t1),u(t1)),有 与(10)矛盾.因此I(u)<0,∀t ∈[0,T).从而V′(t)>0,V(t)在[0,T)单调递增,即(ut,u)≥(u1,u0),∀t ∈[0,T). 接下来证明问题(1)解的有限时刻爆破性质,并估计爆破时间的上界.对于任意的T1∈(0,T),定义如下函数 其中ω,ν为正常数.容易算得 再用Schwarz不等式,可以得到 由(6),引理2.4,(2),(8)和(13),有 再结合Schwarz不等式以及(ut,u)≥(u1,u0),∀t ∈[0,T),可以得出 由(10)可知 把上述(G′(t))2和G′′(t) 的结果代入下式,很容易得到 时,有G′(0)>0.进一步由引理2.1可得 其中ξ:=ων,又由(19)可得 由(18)可得 现在求h(ξ,ν)的下确界,其中ξ满足(20),ν满足(21),则 由T1∈(0,T)的任意性可得 注1定理3.1展现了一个新的与d无关的有限时刻爆破条件,而且这个条件蕴含着I(u0)<0.因此,与[12]中定理5.6 相比,它不需要再考虑Nehari泛函的初始值I(u0)的符号问题. 定理3.2假设(M0)成立,f满足(S1)-(S4),u0∈W0,u=u(x,t)是问题(1)的弱解,那么问题(1)的解在任意高初始能量下是有限时刻爆破的,即不论E(0)取何值,都有 证可以取得σ(x)∈W0和γ(x)∈L2(Ω),且σ(x),γ(x)≠0,使得(σ(x),γ(x))=0.对任意的常数D,令 其中a,b为正常数.容易算得 由E(t)的定义,有 令引理2.3中u=σ,ϑ=a,得到 接下来从两种情况进行分析,证明问题(1)的解在任意高初始能量下有限时刻爆破. 情况1. 根据(23),能够找到足够大的a使得 对上述a,取 对上面取得的a和b,令 再结合(22),(24),(25),可以得到, 即初始能量E(0)满足(9),结合定理3.1 的(i),有 情况2. 根据(23),能够找到足够大的a使得 对上面取得的a和b,令 再结合(22),(26),(27),可以得到 即初始能量E(0)满足(10),结合定理3.1 的(ii)可得 注2定理3.2得到了问题(1)的解在任意高初始能量下的有限时刻爆破,是对[12]中定理5.6的低初始能量下爆破结果的进一步推广.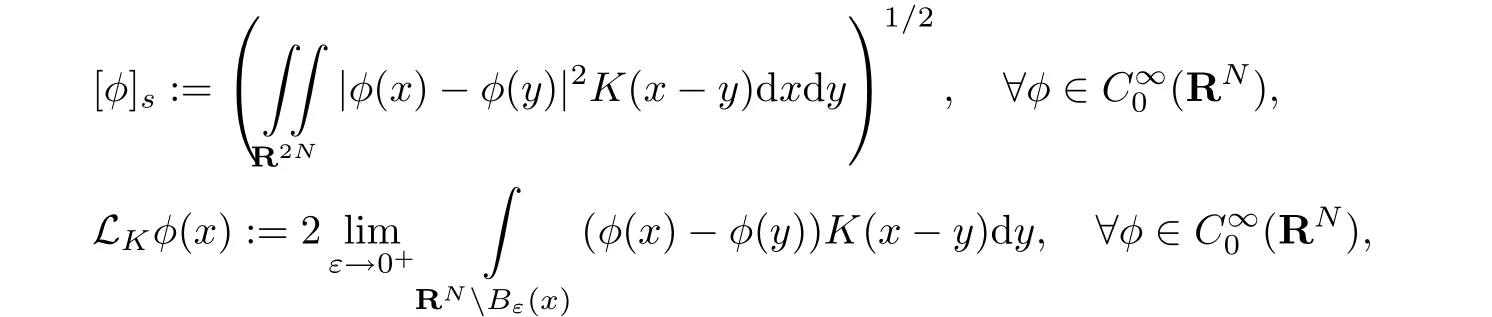


§2 预备知识
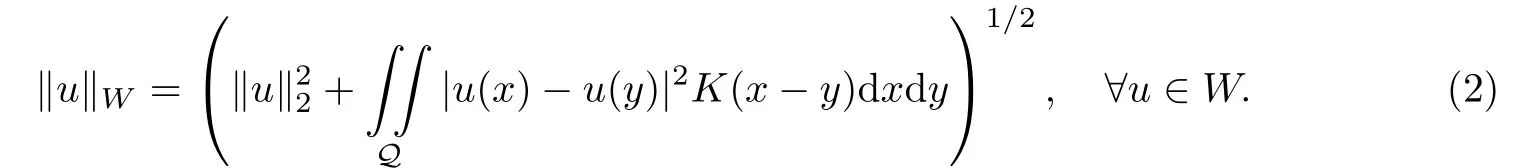
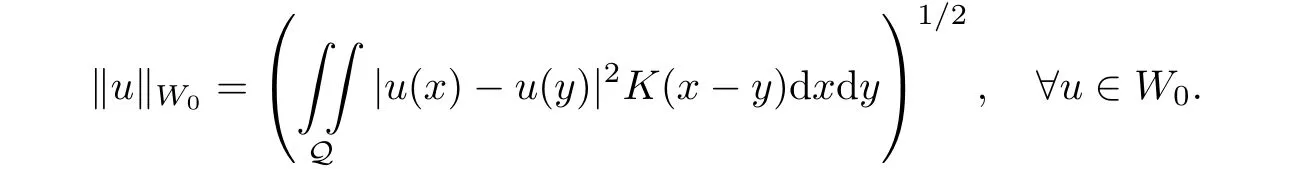
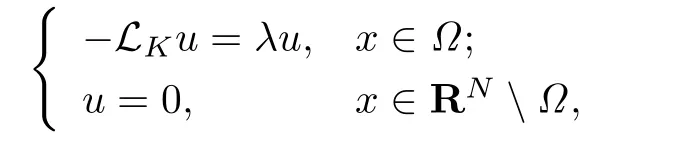
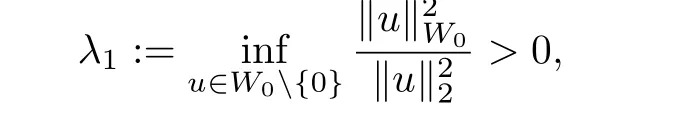



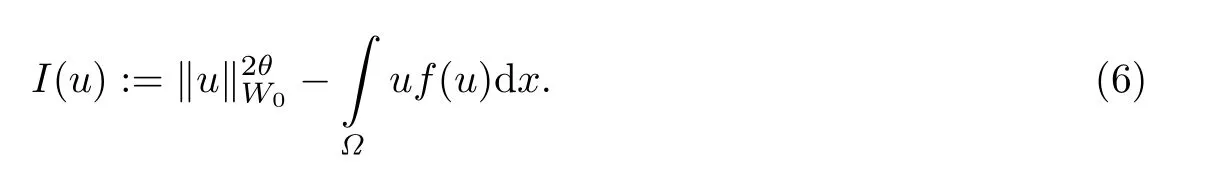
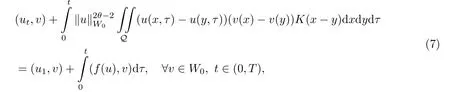

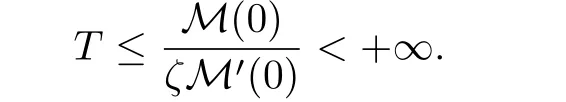
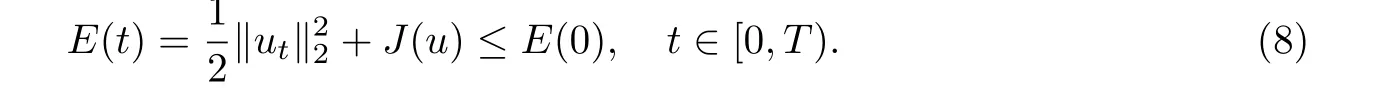
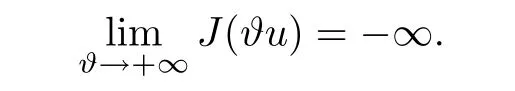


§3 主要结果