非对合剩余格的模糊理想理论
2021-12-28刘春辉
刘春辉
(赤峰学院 数学与计算机科学学院,内蒙古赤峰 024001)
§1 引言
在经典的二值逻辑推理中,已知前提所使用的概念和提供的信息都是精确的,就能保证推得的结果也是准确无误的,这种精确的,严格的逻辑推理是人工智能科学及相关研究中普遍采用的方法,并在逻辑程序设计,定理自动证明和知识推理等领域具有广泛应用.它不仅为计算机程序设计语言提供了主要思想,而且在计算机硬件设计中也有一定应用,形成了传统计算机科学的理论基础.然而传统计算机通常只能按照经典逻辑进行识别,对模糊概念和模糊信息的识别和处理却表现得无能为力.为了克服经典逻辑在计算机应用中的不足,1965 年,L.A.Zadeh提出了模糊逻辑的概念[1],从而使计算机不但可以对模糊概念进行处理,还可以在信息有限的情况下,提供精确的答案.模糊逻辑主要采用代数逻辑的研究方法,而后者则以逻辑代数为工具来进行研究,由此可知,逻辑代数在模糊逻辑的研究中起着十分重要的作用[2].在模糊逻辑对应的代数系统研究中,由Ward和Dilworth于1939年在文献[3]中首次提出的剩余格是一类重要且应用广泛的逻辑代数.近年来,剩余格已经被越来越多的学者公认为是模糊逻辑的理想代数框架之一,逐渐成为逻辑代数中最为活跃的研究对象.究其原因,主要体现在以下两方面:其一,剩余格是一类范围较广宽泛的逻辑代数,诸如MTL代数,BL代数,MV代数和Glivenko代数等著名的逻辑代数都是其特殊子类;其二,几乎所有的子结构逻辑,如直觉主义逻辑,多值逻辑,模糊逻辑以及线性逻辑等都是以剩余格为基础来建立相应的代数语义.因此,对剩余格结构的深入研究具有广泛而基本的重要意义,相关研究成果也颇为丰富[4-10].
偏序结构被布尔巴基学派冠名为三大数学母结构之一,滤子和理想最早是作为偏序集的两类相互对偶的特殊子集而被提出的概念.在模糊逻辑理论研究中,滤子和理想又被作为研究模糊逻辑代数及与它们相对应的逻辑推理系统完备性的两个重要工具而进行了扩充和推广.值得注意的是,在否定运算满足对合(正则)性质的逻辑代数中,考虑到滤子和理想是相互对偶存在的,各种理想的性质都可借助于与之相对偶的滤子概念的性质直接获得.所以,人们大都将目光集中于对滤子问题的思考和探索[11-17].然而,当逻辑代数中否定运算失去对合性时,理想和滤子的对偶关系也随之被打破.因此,在非对合剩余格,MTL代数和BL代数等非对合逻辑代数框架下探索理想及其应用问题是一项十分有意义的工作.鉴于此,文献[18]在MTL代数中引入了超理想,素理想和关联理想等概念并考察了它们的性质和相互关系.文献[19]在BL代数中引入了理想概念并研究了其性质及其与滤子概念的关系.文献[20-23]在非对合剩余格中引入了理想和模糊理想的概念并讨论了其相关性质和结构特征.文献[24]在非对合剩余格中引入了正规模糊理想并基于这一概念给出了一致拓扑的构造方法.文献[25]又在MTL代数这一非对合剩余格的特例上基于素理想成功构造了拓扑空间.在上述工作的基础上,本文进一步深入系统地研究非对合剩余格的模糊理想问题,引入了非对合剩余格的模糊弱理想,模糊强理想,模糊MV理想,模糊布尔理想,模糊关联理想,模糊正关联理想和模糊超理想七类概念,系统讨论了它们的性质,等价刻画以及概念之间的相互关系,并利用它们的性质获得了几类特殊剩余格的特征定理.获得了一些有意义且有趣的结果.进一步丰富和完善了非对合剩余格理想问题的理论体系.
§2 预备知识
定义2.1[3]称(2,2,2,2,0,0)型代数(L,≤,∧,∨,⊗,→,0,1)为一个剩余格,简称L为一个剩余格,如果下列各条件成立.
(RL1) (L,∧,∨,0,1)是分别以0和1为最小元和最大元的有界格;
(RL2) (L,⊗,1)是一个以1为单位元的交换半群;
(RL3) (⊗,→)是L上的伴随对,即(∀x,y,z ∈L)(x ⊗y≤z ⇔x≤y→z).
定义2.2[4-8,10]设L是一个剩余格.则
(1) 称L为非对合剩余格,如果L满足:(∃x ∈L)(x′′≠x);
(2) 称L为对合(正则)剩余格,如果L满足:(∀x ∈L)(x′′=x);
(3) 称L为强剩余格(Glivenko代数),如果L满足:(∀x ∈L)((x′′→x)′′=1);
(4) 称L为预线性剩余格(MTL代数),如果L满足:(∀x,y ∈L)((x→y)∨(y→x)=1);
(5) 称L为BL代数,如果L为MTL代数且满足:(∀x,y ∈L)(x ∧y=x ⊗(x→y));
(6) 称L为MV代数,如果L为BL代数且满足:(∀x,y ∈L)((x→y)→y=(y→x)→x).
引理2.1[2-10,18-21]设L是非对合剩余格,则对任意的x,y,z ∈L,下列结论成立.
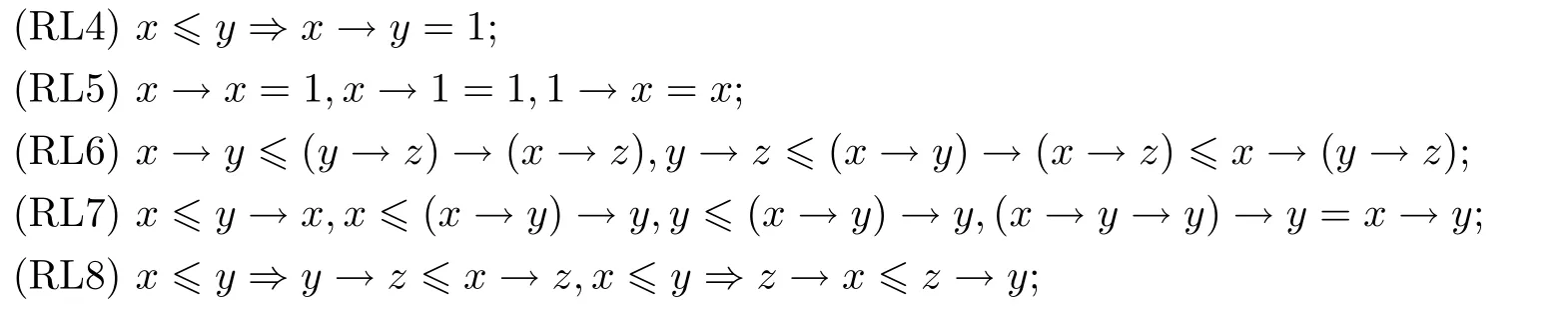

其中,x′=x→0.
定义2.3[18-19]设L是非对合剩余格,∅≠I ⊆L.称I为L的理想,若I满足
(I1) 0∈I;
(I2) (∀x,y ∈L)((x ∈I且(x′→y′)′ ∈I)⇒y ∈I).
注2.1[18]设L是非对合剩余格,则{0}和L显然都是L的理想,称之为L的平凡理想.
定义2.4[1,19]设L是非对合剩余格,L上的一个模糊集f是指映射f:L→[0,1].设f和g是L上的两个模糊集,定义f与g的模糊包含关系满足:∀x ∈L,

设A ⊆L,A的特征函数χA指的是L上的一个按如下方式定义的模糊集:∀x ∈L,

为了叙述简洁,对任意的x,y ∈[0,1],以下分别用x ∨y和x ∧y表示max{x,y}和min{x,y}.
定义2.5[19]设L是非对合剩余格,f为L上的模糊集.称f为L的模糊理想,若f满足
(FI1) (∀x ∈L)(f(0)≥f(x));
(FI2) (∀x,y ∈L)(f(y)≥f(x)∧f((x′→y′)′).
引理2.2[19]设L是非对合剩余格,f为L的模糊理想.则f满足
(FI3) (∀x,y ∈L)(x≤y ⇒f(x)≥f(y)).
§3 非对合剩余格的模糊弱理想和模糊强理想
本节在非对合剩余格中引入模糊弱理想和模糊强理想并考察它们的性质特征.
定义3.1设L是非对合剩余格,f是L上的模糊集.称f为L的模糊弱理想,若f满足(FI1)和
(WFI) (∀x,y ∈L)(f(x)≥f(y)∧f((x→y)′)).
定理3.1设L是非对合剩余格,f为L的模糊弱理想.则f满足(FI3).
证任取x,y ∈L,设x≤y,则由(RL4)得(x→y)′=1′=0,所以由(WFI)和(FI1)得

故f满足(FI3).
定理3.2设L是非对合剩余格.则L的任一模糊理想都是L的模糊弱理想.
证设f是L的模糊理想,则由定义2.5和引理2.2得f满足(FI1)-(FI3).任取x,y ∈L,因为由(RL17)得y′→x′≥x→y,所以由(RL15)得(y′→x′)′≤(x→y)′,从而由(FI3)得f((y′→x′)′)≥f((x→y)′).故再由(FI2)得
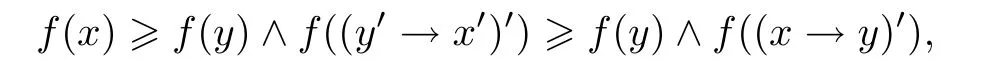
即f满足(WFI).因此,由定义3.1便得f是L的模糊弱理想.
注3.1 下面的例子表明定理3.2的逆命题一般不真.即,非对合剩余格L的模糊弱理想一般不必为L的模糊理想.
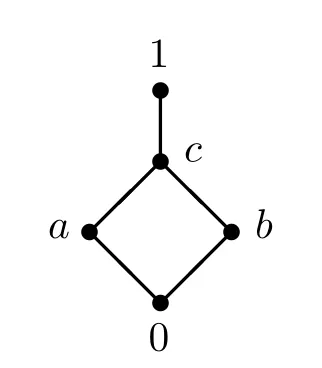
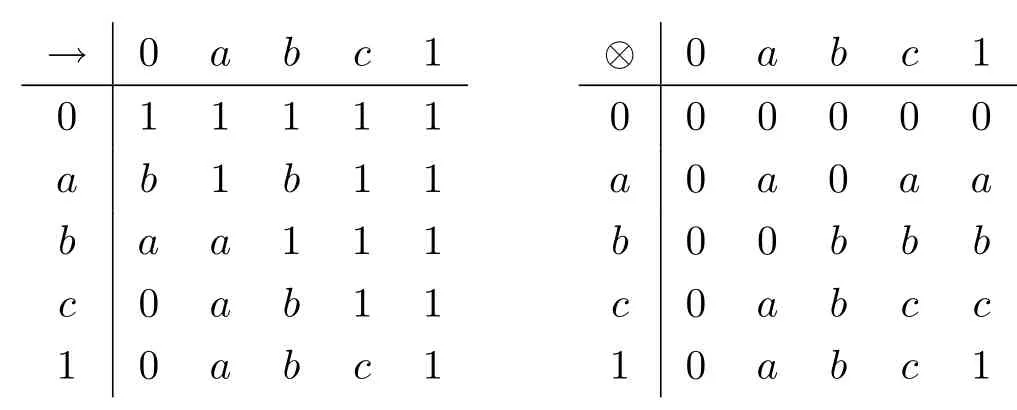
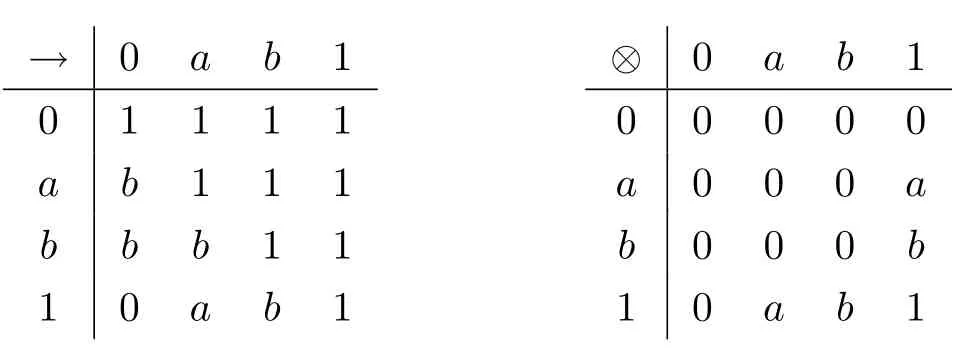
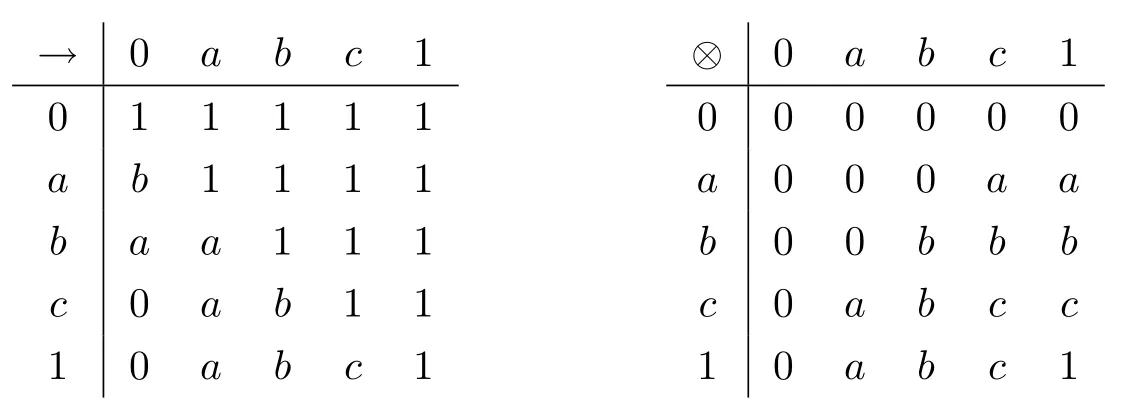
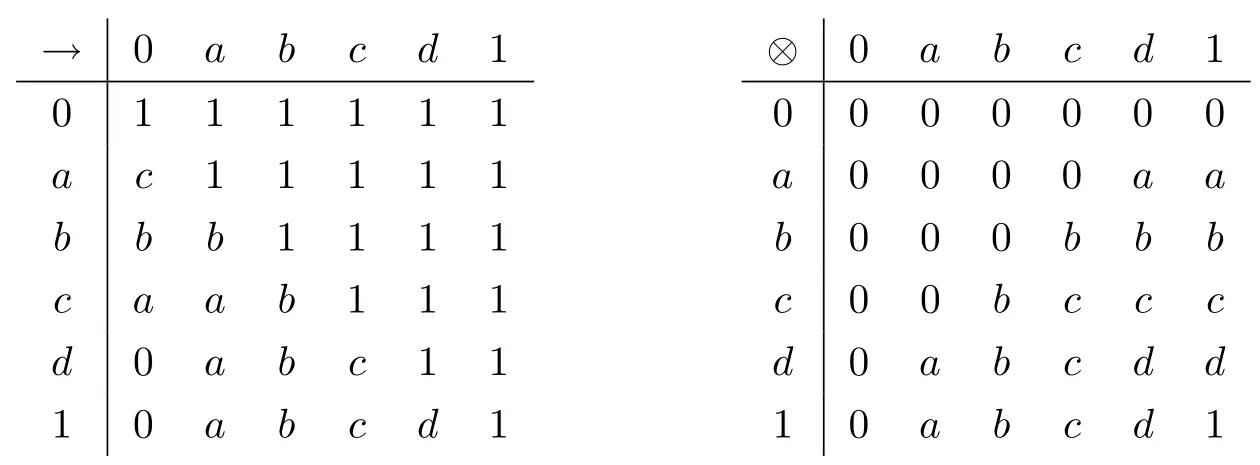
例3.1设格L={0,a,b,c,1}且0 则(L,≤,∧,∨,⊗,→,0,1)是一个非对合剩余格.在L上定义模糊集f:[0,1]→L使f(0)=f(a)=α,f(b)=f(c)=f(1)=β,其中,0 ≤β <α≤1.可以验证f是L的一个模糊弱理想,但非L的模糊理想.这是因为f(a)∧f((a′→b′)′)=f(a)∧f((c→c)′)=f(a)∧f(0)=α >β=f(b),即f不满足(FI2). 定理3.3设L是强剩余格.则L的任一模糊弱理想都是L的模糊理想. 证设L是强剩余格.任取x,y ∈L,因为 所以((y→x)′→(x′→y′)′)′=1′=0.故由(WFI)和(FI1)得 即f满足(FI2).因此由定义2.5便得f是L的模糊理想. 定义3.2设L是非对合剩余格,f是L的模糊理想.称f为L的模糊强理想,若f满足 (SFI) (∀x ∈L)(f((x′′→x)′)=f(0)). 例3.2设格L={0,a,b,c,1}且其Hasse图如图1.定义L上的二元运算→和⊗如下表. 图1 格L的Hasse图 则(L,≤,∧,∨,⊗,→,0,1)是一个非对合剩余格.在L上定义模糊集f:[0,1]→L使f(0)=α,f(a)=β,f(b)=f(c)=f(1)=γ,其中,0 ≤γ <β <α≤1.可以验证f是L的一个模糊强理想. 定理3.4设L是非对合剩余格,f为L的模糊理想.则下列各陈述等价. (1)f是L的模糊强理想; (2) (∀x,y ∈L)(f(((y→x′′)→(y→x)′′)′)=f(0)); (3) (∀x,y ∈L)(f(((x→y)→(x′′→y)′′)′)=f(0)); (4) (∀x,y ∈L)(f(((x′→y)→(y′→x)′′)′)=f(0)). 证(1)⇒(2) 设f是L的模糊强理想.任取x,y ∈L,因为由(RL16)得y→x≤(y→x)′′,所以由(RL6)和(RL8)得x′′→x≤(y→x′′)→(y→x) ≤(y→x′′)→(y→x)′′,从而由(RL15)得((y→x′′)→(y→x)′′)′≤(x′′→x)′.故由(FI3)和(SFI)得f(((y→x′′)→(y→x)′′)′)≥f((x′′→x)′)=f(0). 因此,再由(FI1)便得f(((y→x′′)→(y→x)′′)′)=f(0). (2)⇒(1) 设f满足(2).任取x ∈ L,在(2)中令y=x′′,则由(RL5)和(RL16)得f(0)=f(((x′′→x′′)→(x′′→x)′′)′)=f((1→(x′′→x)′′)′)=f((x′′→x)′′′)=f((x′′→x)′),故f满足(SFI).因此,由定义3.2便得f是L的模糊强理想. (1)⇒(3) 设f是L的模糊强理想.任取x,y ∈L,因为由(RL16)得x′′→y≤(x′′→y)′′,所以由(RL6)和(RL8)得x′′→x≤(x→y)→(x′′→y) ≤(x→y)→(x′′→y)′′,从而由(RL15)得((x→y)→(x′′→y)′′)′≤(x′′→x)′.故由(FI3)和(SFI)得f(((x→y)→(x′′→y)′′)′)≥f((x′′→x)′)=f(0).因此,再由(FI1)便得f(((x→y)→(x′′→y)′′)′)=f(0). (3)⇒(1) 设f满足(3).任取x ∈L,在(3)中令y=x,则由(RL5)和(RL16)得f(0)=f(((x→x)→(x′′→x)′′)′)=f((1→(x′′→x)′′)′)=f((x′′→x)′′′)=f((x′′→x)′),故f满足(SFI).因此,由定义3.2便得f是L的模糊强理想. (1)⇒(4) 设f是L的模糊强理想.任取x,y ∈L,因为由(RL13)得x′′=x′→0 ≥(x′→y)⊗(y→0)=(x′→y)⊗y′且由(RL16)得y′→x≤(y′→x)′′,所以由(RL8)和(RL11)得x′′→x≤ (x′→ y)⊗y′→ x=(x′→ y)→(y′→ x) ≤ (x′→ y)→(y′→ x)′′,从而由(RL15)得((x′→y)→(y′→x)′′)′≤(x′′→x)′.故由(FI3)和(SFI)得f(((x′→y)→(y′→x)′′)′)≥f((x′′→x)′)=f(0).因此,再由(FI1)便得f(((x′→y)→(y′→x)′′)′)=f(0). (4)⇒(1) 设f满足(4).∀x ∈L,在(4)中令y=x′,则由(RL5)和(RL16)得f(0)=f(((x′→x′)→(x′′→x)′′)′)=f((1→(x′′→x)′′)′)=f((x′′→x)′′′)=f((x′′→x)′),故f满足(SFI).因此,由定义3.2便得f是L的模糊强理想. 注3.2由定义3.2,显然可知非对合剩余格L的任一模糊强理想都是L的模糊理想.但是L的模糊理想一般不必是L的模糊强理想.例如,设L是例3.1中所给非对合剩余格,在L上定义模糊集f:[0,1]→L使f(0)=α,f(a)=f(b)=f(c)=f(1)=β,其中,0 ≤β <α≤1.可以验证f是L的一个模糊理想,但非L的模糊强理想.这是因为f((a′′→a)′)=f((b→a)′)=f(c′)=f(b)=β≠α=f(0),即,f不满足(SFI). 定理3.5设L是非对合剩余格,则下列各陈述等价. (1)L是强剩余格(Glivenko代数); (2)L的任一模糊理想都是L的模糊强理想; (3)χ{0}是L的模糊强理想. 证(1)⇒(2) 设L是强剩余格且f是L的模糊理想,则∀x ∈L,由定义2.2(3)得(x′′→x)′′=1,从而由(RL16)得(x′′→x)′=(x′′→x)′′′=1′=0.故f((x′′→x)′)=f(0).因此,f是L的模糊强理想. (2)⇒(3) 因为由注2.1得{0}是L的理想,所以由文献[19]中定理3.17得χ{0}是L的模糊理想,故由(2)便得χ{0}是L的模糊强理想. (3)⇒(1) 设χ{0}是L的模糊强理想,则由定义3.2得χ{0}((x′′→x)′)=χ{0}(0)=1,从而(x′′→x)′=0,故(x′′→x)′′=0′=1.因此由定义2.2(3)便得L是强剩余格. 推论3.1设L是非对合剩余格,则下列各陈述等价. (1)L是强剩余格(Glivenko代数); (2)L的任一模糊弱理想都是L的模糊强理想; (3)χ{0}是L的模糊强理想. 证由定理3.2,定理3.3和定理3.5立即可得. 本节引入非对合剩余格的模糊MV理想并考察其性质,刻画及其与模糊强理想的关系. 定义4.1设L是非对合剩余格,f为L的模糊理想.称f为L的模糊MV理想,若f满足 (MVFI) (∀x,y ∈L)(f((((y′→x′)→x′)→y′)′)≥f((x′→y′)′)). 例4.1设格L={0,a,b,1}且0 则(L,≤,∧,∨,⊗,→,0,1)是一个非对合剩余格.在L上定义模糊集f:[0,1]→L使f(0)=α,f(a)=f(b)=f(1)=β,其中,0 ≤β <α≤1.可以验证f是L的一个模糊MV理想. 定理4.1设L是非对合剩余格,f为L的模糊理想.则下列各陈述等价. (1)f是L的模糊MV理想; (2) (∀x,y,z ∈L)(f((((y′→x′)→x′)→y′)′)≥f(z)∧f((z′→(x′→y′))′)); (3) (∀x,y ∈L)(f((((y′→x′)→x′)→((x′→y′)→y′))′)=f(0)); (4) (∀x,y ∈L)(f(((x′→y′)→(((y′→x′)→x′)→y′))′)=f(0)). 证(1)⇒(2) 设f是L的模糊MV理想.任取x,y,z ∈L,则 (2)⇒(1) 设f满足(2).在(2)中取z=0,则由(FI1)和(RL5)便得f满足(MVFI),因此,由定义4.1得f是L的模糊MV理想. (1)⇒(3) 设f是L的模糊MV理想.任取x,y ∈L,令U=((x′→y′)→y′)′,则 故由(MVFI)得f((((U′→x′)→x′)→U′)′) ≥f((x′→U′)′)=f(0).又由(RL7)和(RL18)得y′≤(x′→y′)→y′=((x′→y′)→y′)′′=U′,所以由(RL8)得U′→x′≤y′→x′,从而(y′→x′)→x′≤(U′→x′)→x′,进而((U′→x′)→x′)→U′≤((y′→x′)→x′)→U′,故再由(RL16)得(((y′→x′)→x′)→U′)′≤(((U′→x′)→x′)→U′)′.于是由(FI3)又得 故再由(FI1)便得f((((y′→x′)→x′)→U′)′)=f(0).因此由(RL18)得 (3)⇒(1) 设f满足(3).任取x,y ∈L,因为 所以f满足(MVFI1),因此由定义4.1便得f是L的模糊MV理想. (3)⇔(4) 任取x,y ∈L,因为由(RL11)得 所以 当且仅当 定理得证. 定理4.2设L是非对合剩余格,则下列各陈述等价. (1)L的任一模糊理想都是L的模糊MV理想; (2)χ{0}是L的模糊MV理想; (3) (∀x,y ∈L)((x′→y′)→y′=(y′→x′)→x′); (4) (∀x,y ∈L)(((x′→y′)→y′)→x′=y′→x′). 证(1)⇒(2) 因为由注2.1得{0}是L的理想,所以由文献[19]中定理3.17得χ{0}是L的模糊理想,故由(1)便得χ{0}是L的模糊MV理想. (2)⇒(3) 设χ{0}是L的模糊MV理想,则由定理4.1中(3)得 从而(((y′→x′)→x′)→((x′→y′)→y′))′=0,进而由(RL18)得 故由(RL4)得(y′→x′)→x′≤(x′→y′)→y′.同理可证(x′→y′)→y′≤(y′→x′)→x′.因此综合便得(x′→y′)→y′=(y′→x′)→x′. (3)⇒(4) 由(3)和(RL7)得 因此(4)成立. (4)⇒(1) 设f是L的模糊理想,任取x,y ∈L,因为由(4)得 所以((x′→y′)→(((y′→x′)→x′)→y′))′=1′=0,故 即f满足定理4.1(4),因此f是L的模糊MV理想. 推论4.1设L是对合(正则)剩余格,则下列各陈述等价. (1)L的任一模糊理想都是L的模糊MV理想; (2)χ{0}是L的模糊MV理想; (3) (∀x,y ∈L)((x′→y′)→y′=(y′→x′)→x′); (4) (∀x,y ∈L)(((x′→y′)→y′)→x′=y′→x′); (5)L是MV代数. 证由定理4.2,只需证明(3)⇔(5)即可.事实上,任取x,y ∈L,因为L是对合剩余格,所以x′′=x且y′′=y.故由(3)得 因此由定义2.2(6)便得L是MV代数.反之,若L是MV代数,由定义2.2(6),显然有(3)成立. 定理4.3设L是强剩余格.则L的任一模糊MV理想都是L的模糊强理想. 证设f是L的模糊MV理想,则由定义4.1得f是L的模糊理想.因此再由定理3.5便得f是L的模糊强理想. 注4.1定理4.3的结论对不是强剩余格的非对合剩余格L而言不一定成立.例如,考虑例4.1中所给非对合剩余格L,因为(a′′→a)′′=(b→a)′′=a′′=b≠1,所以L不是强剩余格.再考虑例4.1中所定义的L的模糊MV理想f,因为f((a′′→a)′)=f((b→a)′)=f(b′)=f(b)=β≠α=f(0),所以f不是L的模糊强理想. 注4.2下面的例子表明定理4.3的逆命题一般不真.即强剩余格L的模糊强理想一般不必为L的模糊MV理想. 例4.2设格L={0,a,b,c,1}且0 则(L,≤,∧,∨,⊗,→,0,1)是一个强剩余格.在L上定义模糊集f:[0,1]→L使f(0)=α,f(a)=f(b)=f(c)=f(1)=β,其中,0 ≤β <α≤1.可以验证f是L的一个模糊强理想,但不是L的模糊MV理想.这是因为f((((a′→b′)→b′)→a′)′)=f((((b→a)→a)→b)′)=f(((a→a)→b)′)=f(a)=β <α=f((b′→a′)′)=f(0),即f不满足(MVFI). 定理4.4设L是BL代数,f是L上的模糊集.则下列各陈述等价. (1)f是L的模糊理想; (2)f是L的模糊弱理想; (3)f是L的模糊强理想; (4)f是L的模糊MV理想. 证设L是BL代数,任取x ∈L,因为由文献[19]中命题2.6(17)以及(RL16)和(RL5)得 所以由定义2.2(3)得L是强剩余格.故由定理3.2,定理3.3和定理3.5便得(1)⇔(2)⇔(3).因此为了完成定理的证明,只需证明(1)⇔(4),而由定义4.1可知,只需证明(1)⇒(4)即可.事实上设f是L的模糊理想,任取x,y ∈L,因为 所以f((((y′→x′)→x′)→y′)′) ≥f((x′→y′)′),故f满足(MVFI).则由定义4.1便得f是L的模糊MV理想. 本节引入非对合剩余格的模糊布尔理想,模糊关联理想和模糊正关联理想并考察它们的性质,刻画及相互关系.同时,讨论它们与模糊强理想和模糊强MV理想的关系. 定义5.1设L是非对合剩余格,f为L的模糊理想.称f为L的模糊布尔理想,若f满足 (BFI) (∀x,y ∈L)(f(x ∧x′)=f(0)). 例5.1设格L={0,a,b,1}且0 则(L,≤,∧,∨,⊗,→,0,1)是一个非对合剩余格.在L上定义模糊集f:[0,1]→L使f(0)=f(a)=α,f(b)=f(1)=β,其中,0 ≤β <α≤1.可以验证f是L的一个模糊布尔理想. 定理5.1设L是非对合剩余格,f为L的模糊理想.则下列各陈述等价. (1)f是L的模糊布尔理想; (2) (∀x ∈L)(f(x)≥f((x→x′)′)); (3) (∀x,y ∈L)(f(x)≥f((x→(y→x)′)′)). 证(1)⇒(2) 设f是L的模糊布尔理想.任取x ∈L,由(RL16)得x ∧x′≤(x ∧x′)′′,故 从而由(RL15)得((x ∧x′)′→x′)′≤(x→x′)′.因此,由(FI2),(BFI)和(FI2)得 (2)⇒(3) 设f满足(2),任取x,y ∈L,因为y≤1,所以由(RL5)和(RL8)得x=1→x≤y→x,从而由(RL15)得(y→x)′≤x′,进而由(RL8)得x→(y→x)′≤x→x′,故再由(RL15)得(x→x′)′≤(x→(y→x)′)′.因此,由(2)和(FI3)便得 (3)⇒(1) 设f满足(3),任取x ∈L,因为 所以由(RL15)得((x ∧x′)→(1→(x ∧x′))′)′≤1′=0,从而((x ∧x′)→(1→(x ∧x′))′)′=0.故由(3)得f(x ∧x′)≥f(((x ∧x′)→(1→(x ∧x′))′)′)=f(0),于是再由(FI1)得f(x ∧x′)=f(0),即f满足(BFI).因此由定义5.1得f是L的模糊布尔理想. 定义5.2设L是非对合剩余格,f为L上模糊集.称f为L的模糊关联理想,若f满足(FI1)和 (IFI) (∀x,y,z ∈L)(f(x)≥f(z)∧f((z′→((x′→y′)→x′)′′)′)). 定理5.2设L是非对合剩余格.则L的任一模糊关联理想都是L的模糊理想. 证设f是L的模糊关联理想,则由定义5.2得f满足(FI1)和(IFI).任取x,y ∈L,由(RL5)和(RL16)得 所以由(IFI)得 故f亦满足(FI2).因此由定义2.5便得f是L的模糊理想. 注5.1定理5.2的逆命题一般不真.即非对合剩余格L的模糊理想一般不必为L的模糊关联理想.例如设L是例5.1中所给非对合剩余格,在L上定义模糊集f:[0,1]→L使f(0)=α,f(a)=f(b)=f(1)=β,其中,0 ≤β <α≤1.可以验证f是L的模糊理想,但不是L的模糊关联理想.这是因为f(0)∧f((0′→((a′→1′)→a′)′′)′)=f(0)∧f((a→b)′)=f(0)=α>β=f(a). 定理5.3设L是非对合剩余格,f为L的模糊理想.则下列各陈述等价. (1)f是L的模糊关联理想; (2) (∀x,y ∈L)(f(x)≥f(((x′→y′)→x′)′)). 证(1)⇒(2) 设f是L的模糊关联理想.任取x,y ∈L,因为 所以由(IFI)和(FI1)得 (2)⇒(1) 设f满足(2),任取x,y,z ∈L,因为f为L的模糊理想,所以由(2)和(FI2)得 即,f满足(IFI).因此,由定义5.2便得f是L的模糊关联理想. 定义5.3设L是非对合剩余格,f为L的模糊理想.称f为L的模糊正关联理想,若f满足 (PIFI) (∀x,y,z ∈L)(f((x′→z′)′)≥f((x′→(y′→z′))′)∧f((x′→y′)′)). 定理5.4设L是非对合剩余格,f为L的模糊理想.则下列各陈述等价. (1)f是L的模糊正关联理想; (2) (∀x,y ∈L)(f((x′→y′)′)≥f((x′→(x′→y′))′)); (3) (∀x,y,z ∈L)(f(((x′→y′)→(x′→z′))′)≥f((x′→(y′→z′))′)). 证(1)⇒(2) 设f是L的模糊正关联理想.则f满足(PIFI),在(PIFI)中取z=y且y=x,则由(RL5)和(FI1)便得 (2)⇒(3) 设f满足(2),任取x,y,z ∈L,则由(RL6)得y′→z′≤(x′→y′)→(x′→z′),故由(RL7)得x′→(y′→z′)≤x′→((x′→y′)→(x′→z′)),从而由(RL17)得 进而由(FI3)得f((x′→((x′→y′)→(x′→z′)))′)≥f((x′→(y′→z′))′). 因此便得 (3)⇒(1) 设f满足(3),任取x,y,z ∈L,因为f是L的模糊理想,所以 故f满足(PIFI).因此由定义5.3得f是L的模糊正关联理想. 定理5.5设L是非对合剩余格,f为L的模糊理想,则下列各陈述等价. (1)f是L的模糊布尔理想; (2)f是L的模糊关联理想; (3)f是L的模糊正关联理想. 证(1)⇒(2) 设f是L的模糊布尔理想.任取x,y ∈L,因为由(RL17)得y→x≤x′→y′,所以由(RL8)和(RL17)得 从而由(RL15)得((x′→y′)→x′)′≥(x→(y→x)′)′.故由定理5.1(3)和(FI3)得 因此,由定理5.3便得f是L的模糊关联理想. (2)⇒(3) 设f是L的模糊关联理想.任取x,y ∈L,则由(RL18)和(RL6)得x′→(x′→y′)=x′→(x′→y′)′′≤((x′→y′)′′→y′)→(x′→y′)=((x′→y′)′′→y′)→(x′→y′)′′,所以由(RL15)得(((x′→y′)′′→y′)→(x′→y′)′′)′≤(x′→(x′→y′))′.故由定理5.3和(FI3)得 因此,由定理5.4(2)便得f是L的模糊正关联理想. (3)⇒(1) 设f是L的模糊正关联理想.任取x ∈L,因为 所以f((x′′→(x′′→(x′′→x′)′))′)=f(0).又因为依次由(RL18),(RL16)和(RL17)得 所以又得f(((x→x′)′′→x′)′)=f((x′′→(x′′→x′)′)′).故 因此由定理5.1(2)便得f是L的模糊布尔理想. 定理5.6设L是非对合剩余格.则L的任一模糊布尔理想都是L的模糊MV理想. 证设f是L的模糊布尔理想.任取x,y ∈L,令U=(y′→x′)→x′,则 从而便得 进而由(RL4)得((U→y′)′→(U→y′)′′)′≤(x′→y′)′.故由(FI3)得 于是,由定理5.1(2)得 即f满足(MVFI).因此由定义4.1便得f是L的模糊MV理想. 注5.2定理5.6的逆命题一般不真.即非对合剩余格L的模糊MV理想一般不必为L的模糊布尔理想.例如例4.1中所给非对合剩余格L的模糊MV理想f不是L的模糊布尔理想.这是因为f(a ∧a′)=f(a ∧b)=β≠α=f(0). 定理5.7设L是非对合剩余格.则L的任一模糊布尔理想都是L的模糊强理想. 证设f是L的模糊布尔理想.∀x ∈L,则由(RL7)得x≤x′′→x,故由(RL15)得 进而由(RL12)和(RL16)得 故(x′′→x)′⊗x′′=0.令U=x′′→x,则 故(U′→(U′→1′))′=0,从而由定理5.4(2)和定理5.5得 进而由(FI1)得f((U′→1′)′)=f(0).又因为 故f((x′′→x)′)=f(0),即f满足(SFI).因此由定义3.2便得f是L的模糊强理想. 注5.3定理5.7的逆命题一般不真.即非对合剩余格L的模糊强理想一般不必为L的模糊布尔理想.例如设L是例5.1中所给非对合剩余格,在L上定义模糊集f:[0,1]→L使f(0)=α,f(a)=f(b)=f(1)=β,其中0 ≤β <α≤1.可以验证f是L的模糊强理想,但不是L的模糊布尔理想.这是因为f(a ∧a′)=f(a)=β≠α=f(0). 下面利用模糊布尔理想的性质给出Boole代数的特征刻画. 定义5.4[10]设(L,∧,∨)是有界分配格.如果存在L上的一元运算∗:L→L满足:∀x ∈L,x ∧x∗=0且x ∨x∗=1,则称L是一个Boole代数. 引理5.1[18]任一MTL代数都是有界分配格. 定理5.8设L是MTL代数.则下列各陈述等价. (1)L是Boole代数; (2)L的任一模糊理想都是L的模糊布尔理想; (3)χ{0}是L的模糊布尔理想. 证(1)⇒(2) 设L是Boole代数且f是L的模糊理想,则∀x ∈L,x ∧x′=0.故f(x ∧x′)=f(0).因此由定义5.1得fL的模糊布尔理想. (2)⇒(3) 因为由注2.1得{0}是L的理想,所以由文献[19]中定理3.17得χ{0}是L的模糊理想.因此由(2)得χ{0}是L的模糊布尔理想. (3)⇒(1) 设χ{0}是L的模糊布尔理想,则由定义5.1得χ{0}(x ∧x′)=χ{0}(0)=1,从而x ∧x′=0,进而由(RL20)又得x ∨x′=1.又因为L是MTL代数,所以由引理5.1得L是有界分配格,因此由定义5.4便得L是Boole代数. 本节引入非对合剩余格的模糊超理想概念并考察其性质,刻画及其与模糊布尔理想概念间的关系. 定义6.1设L是非对合剩余格,f为L的非常值模糊理想.称f为L的模糊超理想,若f满足 (UFI) (∀x ∈L)(f(x)=f(0)或f(x′)=f(0)). 例6.1设格L={0,a,b,c,d,1}且0 则(L,≤,∧,∨,⊗,→,0,1)是一个非对合剩余格.在L上定义模糊集f:[0,1]→L使f(0)=f(a)=f(b)=α,f(c)=f(d)=f(1)=β,其中,0 ≤β <α≤1.可以验证f是L的一个模糊超理想. 定理6.1设L是非对合剩余格,f为L的非常值模糊理想.则下列各陈述等价. (1)f是L的模糊超理想; (2) (∀x,y ∈L)((f(x)≠f(0)且f(y)≠f(0))⇒(f((x→y′))=f(0)且f((y→x′))=f(0))). 证(1)⇒(2) 设f是L的模糊超理想.任取x,y ∈L,设f(x)≠f(0)且f(y)≠f(0),则由(UFI)得f(x′)=f(0)且f(y′)=f(0).因为 所以(x′′→(y→x)′′)′=0,从而f((x′′→(y→x)′′)′)=f(0).故由(FI2)和f(x′)=f(0)得 再由(FI1)得f((y→x′))=f(0).类似地,由f(y′)=f(0)可得f((x→y′))=f(0).即f满足(2). (2)⇒(1) 设f满足(2).因为f为L的非常值模糊理想,所以f(1)≠f(0).任取x ∈L,如果f(x)≠f(0),则由(RL5)和(2)得f(x′)=f((1→x)′)=f(0),故f满足(UFI).因此,由定义6.1便得f是L的模糊超理想. 定理6.2设L是非对合剩余格,则L的任一模糊超理想都是L的模糊布尔理想. 证设f是L的模糊超理想,则f是L的模糊理想.任取x ∈L,因为x∧x′≤x且x∧x′≤x′,所以由(FI3)得f(x ∧x′)≥f(x)且f(x ∧x′)≥f(x′).又因为由(UFI)得f(x)=f(0)或f(x′)=f(0),所以f(x ∧x′)≥f(0),故由(FI1)便得f(x ∧x′)=f(0),即f满足(BFI).因此由定义5.1得f是L的模糊布尔理想. 注6.1定理6.2的逆命题一般不真.即非对合剩余格L的非常值模糊布尔理想一般不必是L的模糊超理想.例如设L是例3.2中所给非对合剩余格.在L上定义模糊集f:[0,1]→L使f(0)=α,f(a)=f(b)=f(c)=f(1)=β,其中0 ≤β <α≤1.可以验证f是L的一个模糊布尔理想,但不是L的模糊超理想.这是因为f(a)=β≠α=f(0)且f(a′)=f(b)=β≠α=f(0),即f不满足(UFI). 文献[19]引入了非对合剩余格的模糊素理想和二型模糊素理想的概念并讨论了它们的性质. 定义6.2[19]设L是非对合剩余格,f为L的非常值模糊理想. (1) 称f为L的模糊素理想,若f满足 (PFI) (∀x,y ∈L)(f((x→y)′)=f(0)或f((y→x)′)=f(0)). (2) 称f为L的二型模糊素理想,若f满足 (SPFI) (∀x,y ∈L)(f(x ∧y)≤f(x)∨f(y)). 引理6.1[19]设L是非对合剩余格,f为L的非常值模糊理想.则 (1)L的任意模糊素理想都是L的二型模糊素理想,但反之不真; (2) 当L是MTL代数时,L的任意二型模糊素理想也都是L的模糊素理想; (3)f是L的二型模糊素理想当且仅当f满足 引理6.2[5]设L是MTL代数,则对任意的x,y ∈L都有(x ∧y)′=x′∨y′. 定理6.3设L是MTL代数,f为L的非常值模糊理想.则f是L的模糊超理想当且仅当f既是L的模糊布尔理想又是L的模糊素理想. 证设f是L的模糊超理想,则由定理6.2得f是L的模糊布尔理想.下证f是L的模糊素理想.事实上,任取x,y ∈L,设f(x ∧y)=f(0),若f(x)≠f(0),则由(UFI)得f(x′)=f(0).又因为 所以由(FI3)得f(((x ∧y)′→y′)′) ≥f(x′)=f(0),故再由(FI1)便得f(((x ∧y)′→y′)′)=f(0).于是,由(FI1)和(FI2)便得 这表明f(y)=f(0).因此,由引理6.1便得f为L的模糊素理想. 反之,设f既是L的模糊布尔理想又是L的模糊素理想.任取x ∈L,则由(BFI)得f(x ∧x′)=f(0),故由引理6.1得f(x)=f(0)或f(x′)=f(0),即,f满足(UFI).因此,由定义6.1便得f是L的模糊超理想. 本节最后,指出如下事实. 注6.2在MTL代数中,模糊素理想不必是模糊超理想.例如,容易验证例4.1中所给非对合剩余格是一个MTL代数,在L上定义模糊集f:[0,1]→L使f(0)=α,f(a)=f(b)=f(1)=β,其中0 ≤β <α≤1.可以验证f是L的一个模糊素理想,但不是L的模糊超理想.这是因为f(b)=β≠α=f(0)且f(b′)=f(b)=β≠α=f(0),即,f不满足(UFI). 众所周知,在考察逻辑代数的结构时,各类具有不同形式和特殊性质的滤子和理想概念扮演着重要的角色.本文在非对合剩余格这一重要的否定运算不具有对合(正则)性质的逻辑代数框架下对模糊理想理论作了深入研究,引入了非对合剩余格的模糊弱理想,模糊强理想,模糊MV理想,模糊布尔理想,模糊关联理想,模糊正关联理想和模糊超理想七类概念,获得了它们的若干性质和等价刻画,并利用这些性质给出了强剩余格,MV代数和Boole代数的特征定理.系统分析了七类概念间的相互关系,指明了在非对合剩余格中,模糊布尔理想,模糊关联理想和模糊正关联理想等同;在强剩余格中,模糊弱理想和模糊强理想等同;在BL代数中,模糊强理想和模糊MV理想等同.同时,建立了模糊强理想,模糊MV理想和模糊布尔理想的扩张定理,获得了利用模糊理想构造其特殊子类的方法.这些工作不但进一步充实和丰富了非对合剩余格的模糊理想理论之研究内容,厘清了概念间的层次关系,而且也能为充分利用理想工具揭示基于非对合剩余格的模糊逻辑系统的结构特征提供理论基础上的支持和保障. 最后为直观起见,将文中得到的非对合剩余格的各类模糊理想概念间关系图示如下. 图2 非对合剩余格中各类模糊理想概念间的相互关系
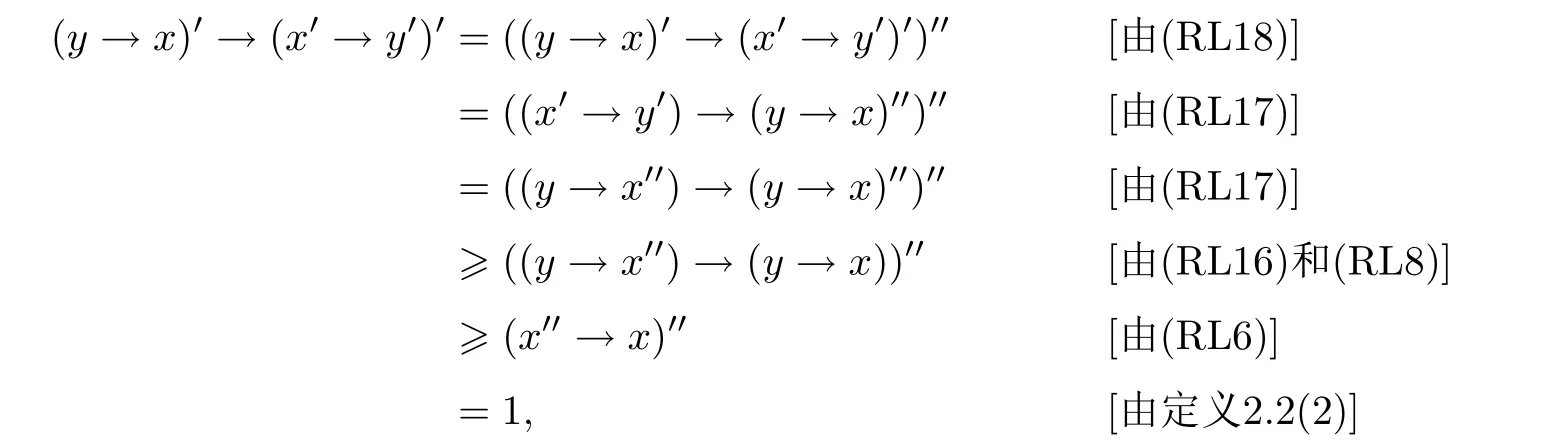

§4 非对合剩余格的模糊MV理想
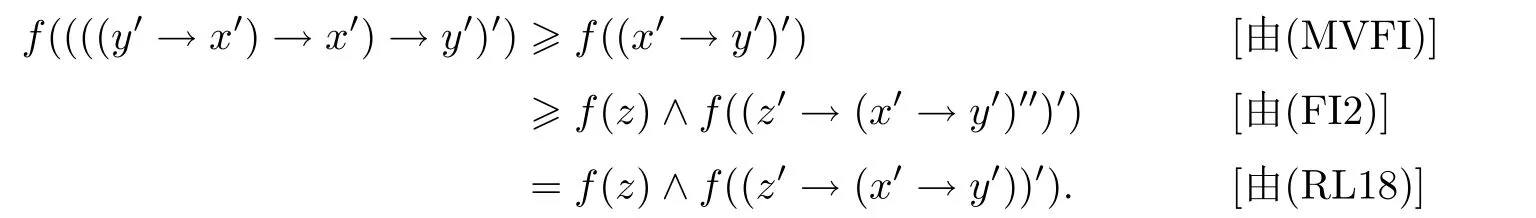
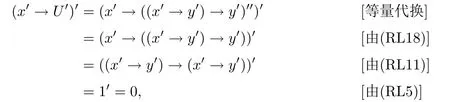

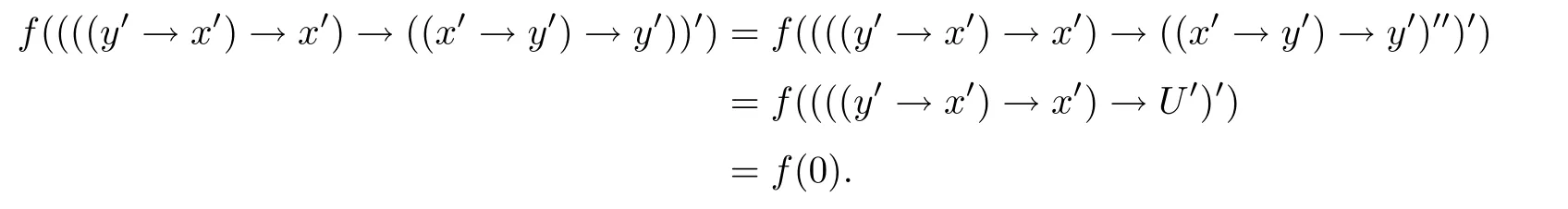


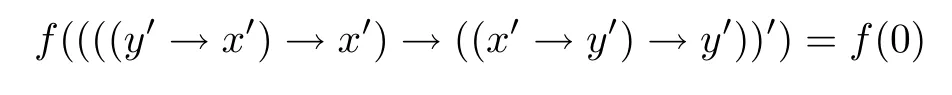

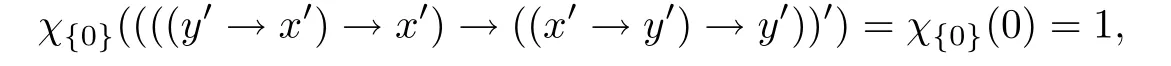
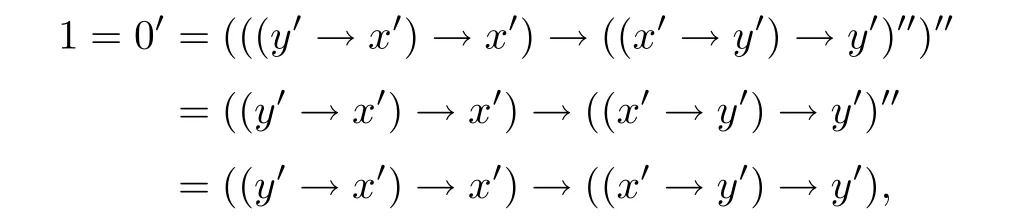

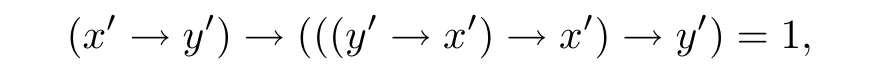

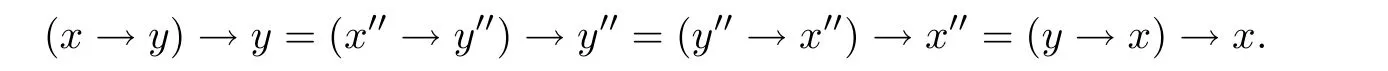
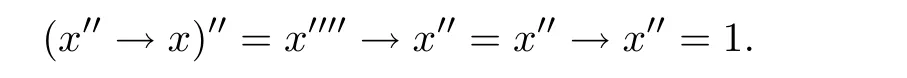

§5 非对合剩余格的模糊布尔(关联和正关联)理想











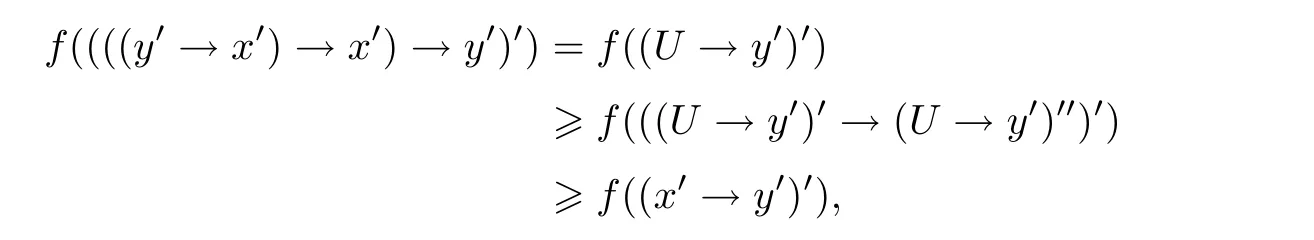
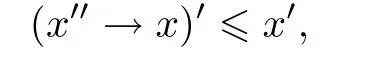
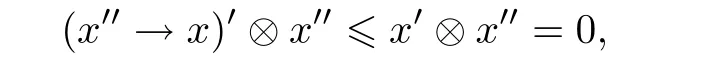
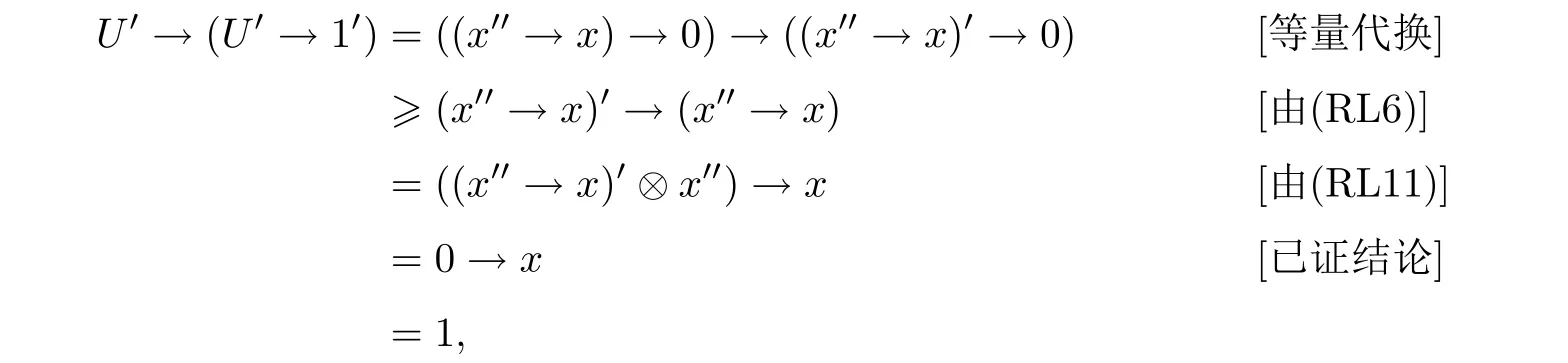

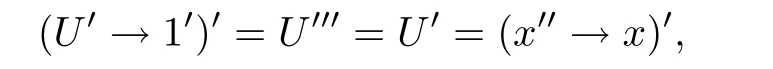
§6 非对合剩余格的模糊超理想
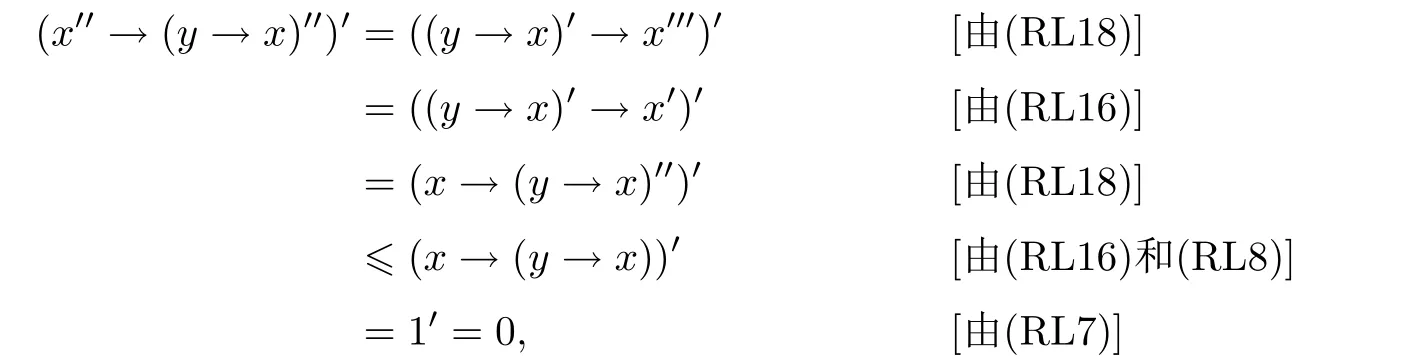

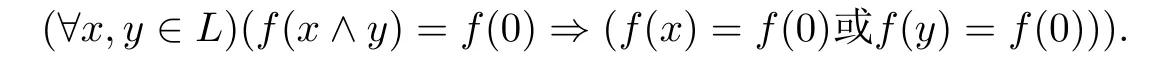
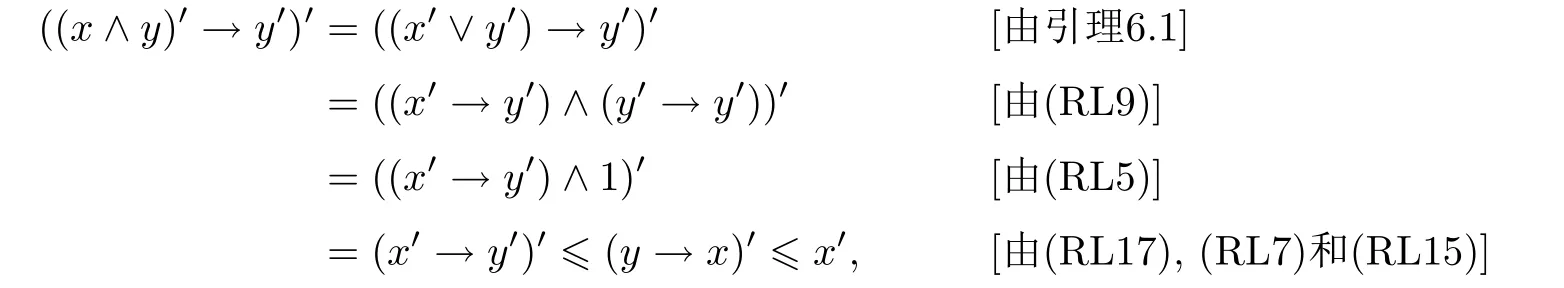
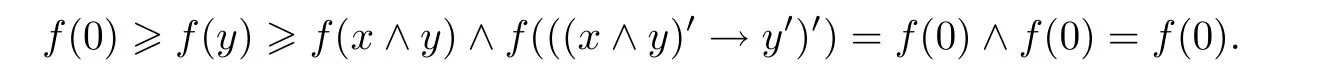
§7 结束语

