基于逆协方差交叉融合的多传感器非线性滤波器

刘金钢，郝 钢

(黑龙江大学 电子工程学院，哈尔滨 150080)

0 引 言

在实际控制系统中，大多数系统是非线性的，深入分析和研究非线性系统可有效解决实际生活中的非线性问题。非线性滤波算法作为非线性系统理论的重要分支，受到了学者们的关注并被广泛应用到目标跟踪，信号处理，导航制导等工程领域[1]。

为了解决非线性系统滤波问题，扩展卡尔曼滤波算法(EKF)[2-3]最早被提出。EKF算法采用泰勒级数展开的方式对非线性方程线性化，然后利用雅可比矩阵代替状态转移矩阵，最后利用卡尔曼滤波方法进行估计。EKF算法容易实现，但需要计算雅可比矩阵，计算量大，同时在线性化时舍弃了高阶项会造成信息缺失，可能导致结果发散。随后UKF[4-5]算法被提出。UKF算法并没有直接近似非线性方程而是利用UT变换生成Sigma点来逼近非线性函数的后验分布。采用UT变换获得Sigma采样点，通过非线性函数传递，用新的采样点近似非线性函数的后验均值和方差。相比于EKF，它不需要计算雅可比矩阵并且滤波精度可以达到二阶泰勒级数展开的精度。近几年，CKF算法[6]被提出。CKF算法从数值积分的角度出发近似高斯积分。三阶球面-相径容积规则[7]通过容积规则得到容积点，经过非线性函数传递，用这些传递后的容积点近似状态后验分布。与EKF、UKF相比，CKF不仅滤波精度高而且稳定性更好。

随着科学技术的发展，单一的传感器很难满足人们的需求，因此多传感器信息融合滤波理论被提出。融合估计通常分为集中式融合和分布式融合[8]。相比于集中式融合，分布式融合不是最优的，但在计算成本，鲁棒性和灵活性等方面的良好性能使其被广泛应用。通常为了求得最优分布式融合估计需要已知各个传感器的互协方差，但在实际应用中互协方差未知或很难得到，因此协方差交叉融合(CI融合)[9-13]算法被提出。该算法不仅不需要已知协方差就可以得到满意的融合效果，而且具有鲁棒性，但也因此过于保守。为了改进CI融合算法，椭圆交叉(EI)[14]算法被提出，该算法减小了估值间公共信息的重复计算，但它不具有一致性。因此在EI算法的基础上提出了逆协方差交叉(ICI)[15-16]算法，该算法不仅具有一致性而且精度高于CI融合[17]。为了降低计算量并提高融合效率，序贯ICI算法被提出并被广泛应用[18-21]。该算法不需要解决高维的权系数凸优化问题,但是当传感器数量太多时，序贯ICI算法会因为多次顺序融合消耗大量的时间。

本文针对互协方差未知的多传感器非线性融合估计问题，提出了基于序贯逆协方差交叉和并行逆协方差交叉的两种容积卡尔曼滤波算法。子系统滤波器采用CKF不仅可以避免因求解雅可比矩阵而带来的巨大的计算量，且具有较高的滤波效果。在对局部估计进行融合时采用序贯ICI和并行ICI两种算法，不仅可以避免高维的权系数凸优化问题，而且当传感器数量特别多时，并行ICI可以有效缩短融合时间。仿真结果证明了两种算法的有效性。

1 问题阐述

考虑多传感器非线性离散系统：

xk+1=fk(xk)+wk

(1)

(2)

(3)

其中:E为数学期望；T为转置，Kronecker函数满足：δii=1,δij=0(i≠j)。

2 容积卡尔曼滤波算法(CKF)

容积卡尔曼滤波算法[6]如下：

1) 初始化：

(4)

2)时间更新：

分解：

(5)

计算容积点：

(6)

其中：

(7)

容积点经过非线性函数传递：

(8)

一步预测的估计与误差方差：

(9)

(10)

3)量测更新：

分解：

(11)

计算容积点：

(12)

容积点经过非线性函数传递：

(13)

量测一步预测，误差方差及互协方差：

(14)

(15)

(16)

滤波增益：

(17)

状态估计与误差方差：

(18)

(19)

3 基于序贯ICI和并行ICI融合的容积卡尔曼滤波器

3.1 CI融合和ICI融合

引理1协方差交叉融合算法[9-10，22]

(20)

(21)

其中ω∈[0，1]极小化性能指标:

(22)

引理2逆协方差交叉融合算法[15-16]

(23)

(24)

(25)

(26)

其中ω∈[0，1]并且满足极小化性能指标：

(27)

引理3[15]对于任意一个ωCI∈[0，1]，总存在一个ωICI=1-ωCI使得PICI[ωICI]≤PCI[ωCI]

3.2 序贯逆协方差交叉容积卡尔曼滤波(SICI-CKF)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

SICI-CKF估值器融合结果为

(36)

其中:ω1,ωi∈[0，1]满足极小化性能指标：

(37)

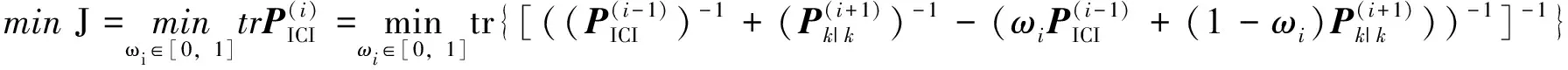
(38)

序贯逆协方差交叉容积卡尔曼滤波器的结构见图1。

图1 SICI-CKF结构Fig.1 SICI-CKF fusion structure

3.3 并行逆协方差交叉融合容积卡尔曼滤波(PICI-CKF)

当系统中存在L个传感器时，采用序贯ICI算法需要进行L-1次两两融合，当L较大时需要消耗大量的时间。因此基于并行协方差交叉(PCI)[23]算法提出了并行逆协方差交叉的容积卡尔曼(PICI-CKF)滤波融合算法。PICI融合算法是由多个并行的两传感器ICI融合算法估值器构成的，以5个传感器为例，其结构见图2。

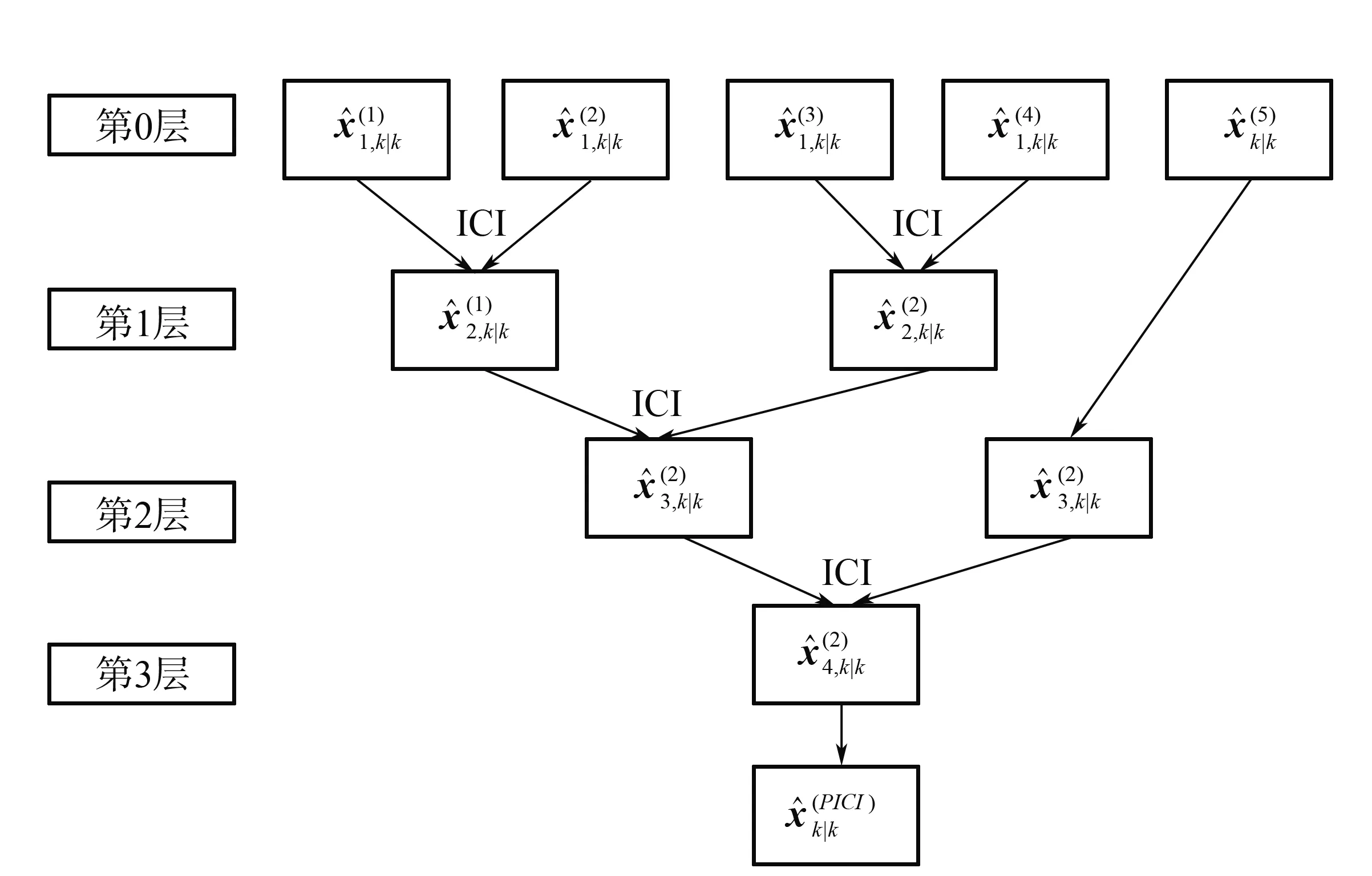
图2 PICI-CKF结构Fig.2 PICI-CKF fusion structure

(39)

(40)

(41)

(42)

其中：Lj为第j层滤波器个数；Lp为最终层数。初值：

(43)

(44)

注1：当有L个传感器需要融合时，假设每次融合时间为τ，则SICI算法需要时间(L-1)τ，而采用PICI算法时，由于每层都是多个两传感器ICI融合同步进行，若有Lp层，则需要时间Lpτ。例如当L=100时，SICI算法需要的融合时间为99τ，而PICI算法将100个估计分成7个并行层进行融合，仅需要时间7τ。与PCI算法[23]相同，传感器个数L不变，第j层两传感器ICI融合器的个数会随着j的增大成指数递减。因此当L特别大时，PICI算法可以节约大量的计算时间。

注2：由引理3可知两传感器估计融合时ICI的精度高于CI的精度。因此所提出的PICI的融合精度高于PCI。

4 仿真分析

为了验证算法的有效性，采用在水平平面上的常转弯率模型：

(45)

(46)

Q(1)=diag(0.52m2·s-4,0.003 32mrad·s-4);Q(2)=diag(0.522m2·s-4,0.0032mrad·s-4);

Q(3)=diag(0.532m2·s-4,0.003 12mrad·s-4);Q(4)=diag(0.552m2·s-4,0.003 42mrad·s-4);

估计性能指标为k时刻位置的累积均方根误差(ARMSE)[20,21]

(47)

真实运动曲线和基于PICI-CKF估计跟踪曲线见图3。由图3可见，基于PICI-CKF的融合估计器具有较高的融合精度。为验证算法有效性进行50次蒙特卡罗实验，传感器1-4局部估计,集中式(CF),SCI-CKF,SICI-CKF,PCI-CKF和PICI-CKF估计的ARMSE见图4。由图4可见，SICI-CKF和PICI-CKF的融合精度明显高于SCI-CKF和PCI-CKF的融合精度，低于集中式的融合精度。且PICI-CKF的融合精度与SICI-CKF的融合精度几乎一致。结果表明所提出的算法具有较高的融合估计精度。

图3 真实和PICI估计跟踪Fig.3 True and estimated tracks of PICI

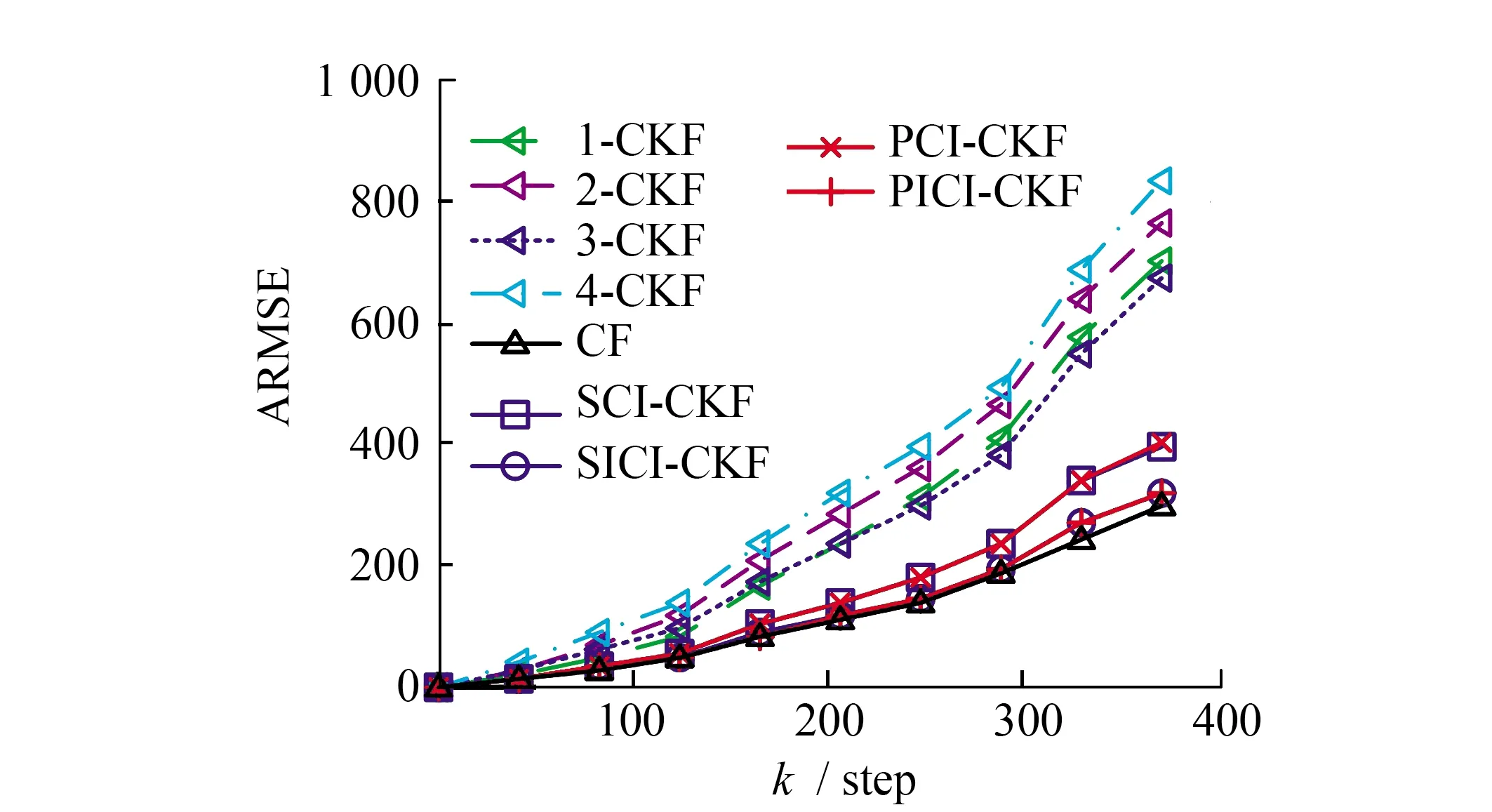
图4 传感器1-4，CF,SCI-CKF,SICI-CKF,PCI-CKF和 PICI-CKF的ARMSE曲线Fig.4 ARMSEs of sensors 1-4, CF, SCI-CKF, SICI-CKF, PCI-CKF and PICI-CKF

5 结 论

针对多传感器非线性系统提出了基于SICI和PIC的两种CKF融合滤波算法。相比于其他算法SICI-CKF融合算法和PICI-CKF融合算法都可以处理在互协方差未知情况下的非线性融合估计问题，同时可以避免处理高维的权系数凸优化问题，降低了计算量;当传感器数量不多时，两种算法的计算时间差距不大，但当传感器数量较大时，PICI-CKF融合算法可大幅度提高融合速度；仿真结果证明SICI-CKF融合算法和PICI-CKF融合算法具有较高的融合精度。