多能源送端电网暂态能量平衡快速鲁棒控制模型

陈伟伟,张增强,毕立松,余中平,张文朝,关洪浩,于国康

（1.国网新疆电力有限公司经济技术研究院，新疆乌鲁木齐 830002；2.新疆大学，新疆乌鲁木齐 830046；3.北京科东电力控制系统有限责任公司，北京 100192）

0 引言

随着我国电力系统规模的不断扩大和可再生能源、多源储能、多能源转换等接入容量的快速增加，远距离大容量输电系统、区域互联系统间功率交换和功率平衡问题日益复杂。多能源接入与大规模跨区送电，使电网在经历大扰动中选择系统稳定优化控制策略和在严重故障下选择合适的安全稳定控制措施，变得更加困难[1]，[2]。

目前，电力系统暂态过程能量平衡控制中，最常用的安全稳定控制策略是针对同步电源的功率控制或切机控制。国内外专家针对不同类型故障下保证电力系统暂态能量平衡功率控制决策开展了较多的研究。文献[5]以稳定性能指标作为暂态能量控制约束条件，通过反向积分计算得到反映当前故障的线性不等式，再通过迭代计算得到最优机组功率控制策略。文献[6]分析了不同故障形式下多种稳定形态的分类和原理，为研究不同故障形式下的功率控制策略奠定了基础。文献[7]将故障切除时发电机的转子角速度和动能作为暂态能量平衡控制策略优化的关键指标。文献[8]综合系统拓扑和暂态功率控制前后发电机同步系数进行动态网络同步化，通过电力系统线性和非线性模型确定最优功率控制策略的切机量。文献[9]基于转子运动方程，分析了电力系统在正常工况下、故障切除时刻和采取机组功率控制措施时刻的运行特性，提出一种求取最小功率控制切机量的方法。文献[10]，[11]研究了相轨迹斜率对暂态能量控制策略及机组功率控制的影响，提出一种功率控制策略表的整定措施。

本文针对送端系统在经历大扰动下的暂态能量平衡过程，提出基于送端电网惯性及状态参数表征的能量平衡过程的动力学模型，并以该动力学模型的离散状态空间表达和送端电网阻尼特性，建立暂态能量预测控制模型；进而在考虑多能源接入后的系统阻尼不确定性基础上，建立多能源送端电网能量平衡鲁棒优化控制模型。本文以河北某典型的送出系统为仿真算例，对所提出的暂态能量控制模型进行了仿真验证。

1 送端电网暂态能量模型

考虑弱送端电网中电、热、气等多能源源荷特性的送端电网等值模型如图1所示。

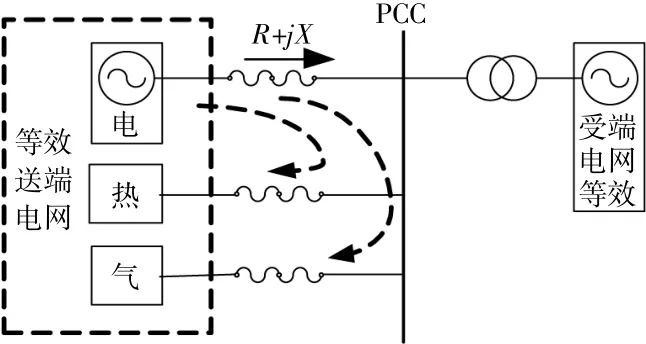
图1 外送电网等值模型Fig.1 Equivalent model of external transmission grid

电、热、气多能源耦合矩阵如下式所示：

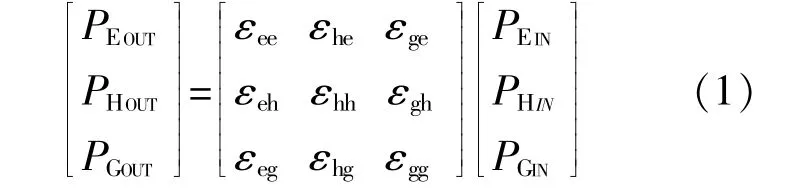
式中：ε为能源间的耦合系数。

送端系统内的电、热、气子系统间存在惯性差异。若电网惯性时间常数为Δt1，热网惯性时间常数为Δt2，气网惯性时间常数为Δt3，且Δt2>Δt3>>Δt1，当系统内电力负荷出现波动时，可在短时间尺度内调节热负荷及气负荷容量，从而优化送端系统的实时功率平衡特性。

设送端电网中热力系统及燃气系统可调节的容量为

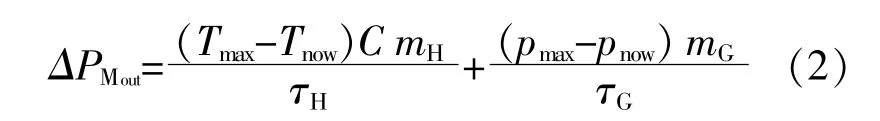
式中：T为传输介质温度；C为传输介质的比热容；mH为热力系统传输介质流量；p为压强；mG为燃气系统气体流量；τH，τG分别为热力系统和燃气系统的惯性时间常数。

发电机可调节容量约束为

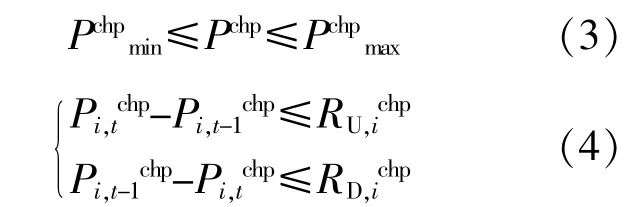
式中：Pchpmin，Pchpmax分别为热电联产机组电功率下限和上限；RU，tchp，RD，tchp分别为热电联产机组的爬坡速率和滑坡速率。

设送端电网的等值惯量为Mou、等值机械功率为Mou、等值电磁功率为PEou；受端电网的等值惯量为Min、等值机械功率为PMin、等值电磁功率为PEin，则送受端系统的转子运动方程为

式中：M，PM，PE分别为等值系统惯量、等值系统机械功率和等值系统的电磁功率。

根据式（11），若利用热力系统以及燃气系统中较大的时间惯性，对特定时间尺度内送端电网负荷总量进行控制，当送端电网在大量失负荷时，则可通过送端电网中的电、热、气等多能源协调，对受端电网的能量输出进行紧急控制。控制原理如图2所示。

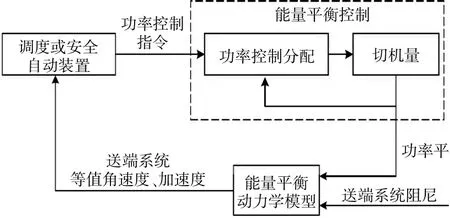
图2 送端电网暂态能量平衡控制原理Fig.2 Principle of transient energy balance control of transmission-end power grid

由图2可知，根据送端系统的能量控制需求，要根据送端电网频率变化的角速度、加速度等动力学状态，对系统中电、热、气等多能源系统的源荷特性进行动态调节。

送端电网电源能量控制过程表示为

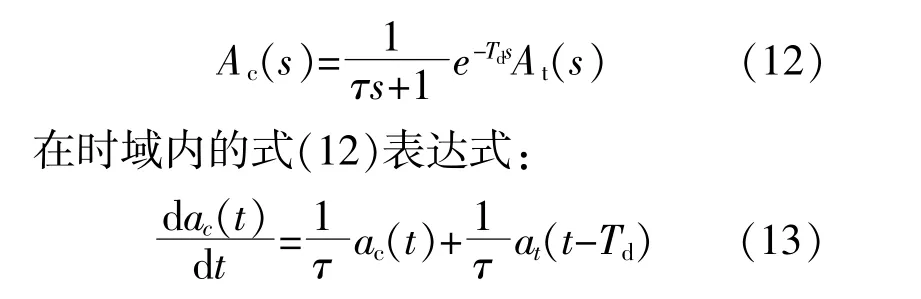
式中：ac（t）为送端电网等值同步电源转子加速度；at（t）为功率控制拟获得的目标加速度；τ为送端系统总的惯性时间常数；s为复参变量；Td为送端系统功率控制系统的延时。

根据式（12），（13）可知，送端电网在紧急能量平衡控制时，能量变化动态过程的状态方程为

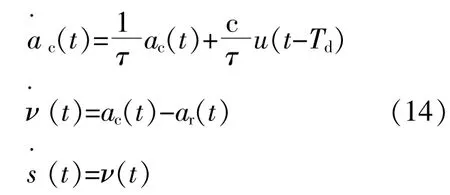
式中：ν（t），s（t）分别为送端电网电源等值同步模型中的转子转速和功角。

在实际电网的功率紧急控制中，无论是调度指令，还是控制装置指令，均是根据对系统状态的实时观测值进行优化控制。将式（14）离散化，并以Δu的形式表示系统功率控制指令：

式中：

式中：T为送端系统各物理量采集的样本时间间隔；l=Td/T，为状态方程时延；w（k）为送端电网总等值阻尼；u（k）为系统在进行紧急状态能量平衡控制过程中的功率控制量，在暂态能量控制中，一般可等效为切机量。

2 送端电网暂态能量预测控制模型

当送端电网的网络拓扑和阻尼参数已知时，将w（k）作为前馈项，可将预测模型线性化表示：

送端电网暂态能量平衡过程的预测时域和控制时域均取为N，则送端电网能量平衡的动态预测控制问题可描述为在送端电力系统状态变量的每一个采样时刻k，求解一个二次型优化问题PN（Δu）：

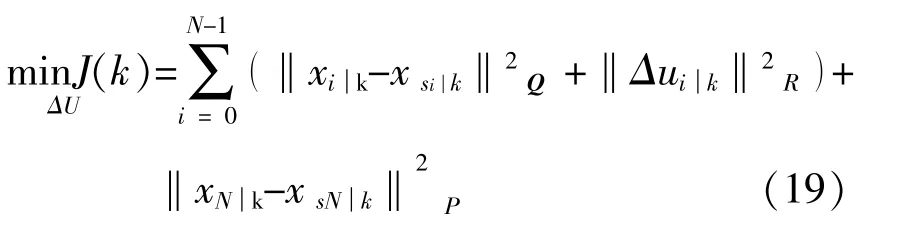
式中：xsi｜k为送端系统等值同步电源的转子运动状态；Q为描述送端系统转子运动状态各参数权重的对称矩阵；R为送端系统能量控制过程中功率控制量权重；‖xN｜k-xsN｜k‖2P为系统中各同步机功角相对偏离惩罚函数，选取适当的R，以获得暂态过程中各采样时刻合适的切机量增量及其变化率；‖xi｜k-xsi｜k‖2Q为送端系统转子运动状态跟踪函数。

PN（Δu）的约束为

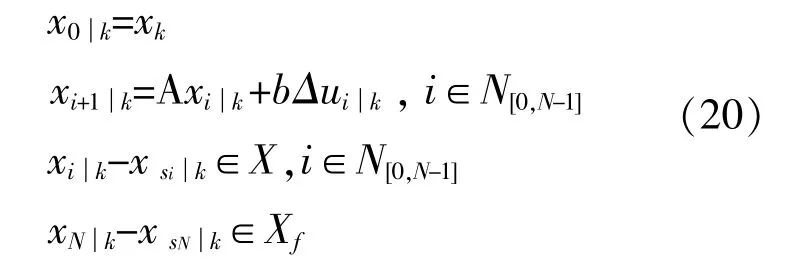
式中：xk为送端系统等值同步电源状态在采用时刻k的实际值；X为送端系统等值同步电源状态跟踪误差的可行集，可由转子运动状态预测值xi｜k与转子运动状态观测值xsi｜k得到；N[0，N-1]为从0到N-1的整数；Xf为送端系统在能量平衡控制结束时状态向量的稳态集合。

通过求解送端电网暂态能量平衡控制优化问题PN（Δu），可得暂态能量平衡控制的最优功率控制向量：

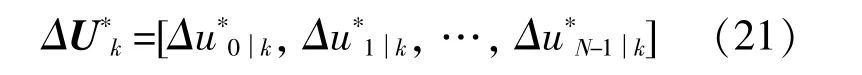
送端电网暂态能量控制过程中，在k时刻施加了Δu*0｜k切机量指令后，当送端系统运行到下一时刻k+1时，在新运行状态测量参数下，继续求解送端系统功率控制量优化问题PN（Δu），将系统的能量平衡控制在时域内进行动态优化。

3 多能源送端电网暂态功率鲁棒控制器

送端电网暂态能量平衡的优化控制问题PN（Δu）模型是在考虑送端系统阻尼已知且恒定不变前提下的控制模型。当送端电网接入较大规模的可再生能源发电、电制热负荷等多能源设备和设施后，送端系统的阻尼状态可能随时间非线性变化，且可能具有较大的不确定性。

由于阻尼不确定性及其波动范围较大，本文采用t Location-scale分布对阻尼不确定性带来的预测误差进行分析。t Location-scale分布的概率密度函数表达式为

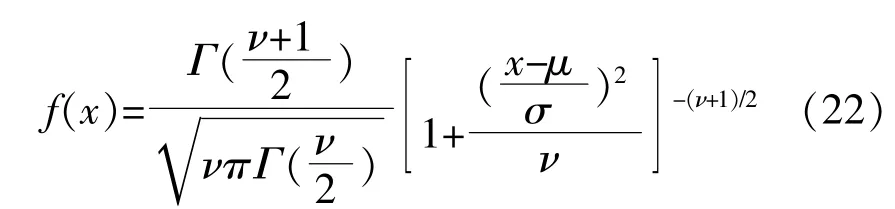
式中：Γ（x）为伽马函数；σ为尺度参数；ν为自由度；μ为位置参数；如果y=（x-μ）/σ，则y服从由自由度为ν的t分布。

阻尼不确定性对电网暂态过程中状态变量预测误差影响的优化问题可表示如下：

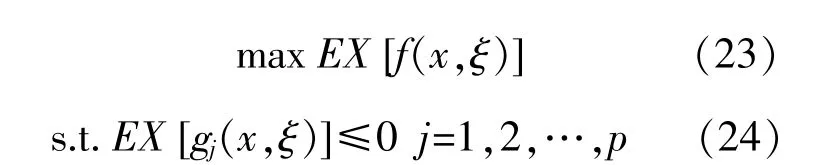
式中：x为n维电网暂态状态向量；ξ为t维的阻尼不确定性随机向量，其概率密度函数为Φ（ξ）；f（x，ξ）为目标函数；gj（x，ξ）为随机约束函数；EX为期望值算子。

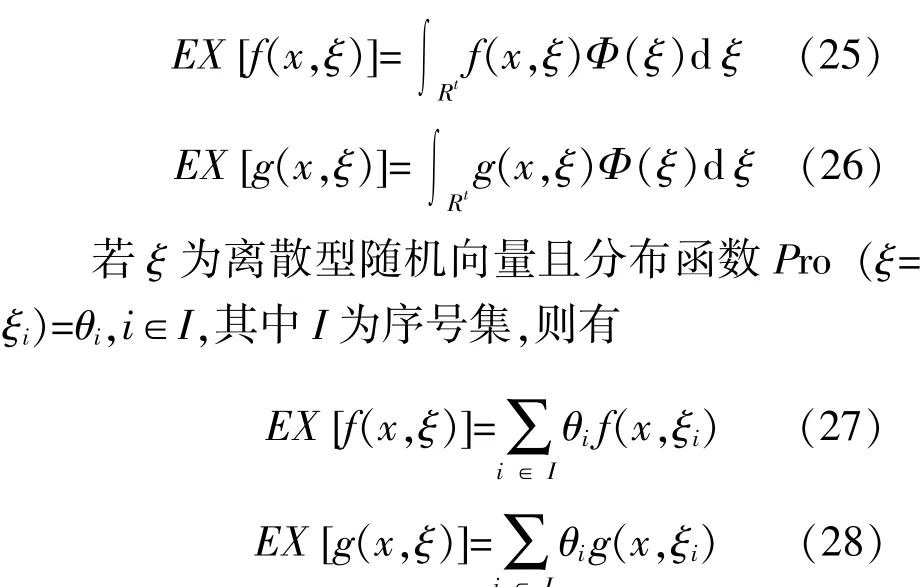
当可行解x*是期望值模型的最优解时，对任意的可行解x，EX[（x*，ξ）]≤EX[f（x，ξ）]成立。

多能源送出电网中，在系统阻尼不确定条件下，设送端电网阻尼不确定性为有界集合w∊W。在预测控制模型的各控制时刻的优化中，仍设N时刻后采用反馈控制策略，以计算送端系统的功角偏离惩罚函数和状态跟踪函数，对阻尼不确定性带来的预测控制误差进行修正：

式中：K∊Rn，且使Acl=A+bK为Hurwitz阵。

送端电网暂态能量平衡过程中，各发电机初始功角和转速分别为s0，ν0，送端电网暂态过程中允许最大转子加速度为a0，送端系统允许的功角摆动曲线为xsk+1=Axsk，则此时送端暂态能量平衡控制在阻尼w下的转子运动状态跟踪误差为

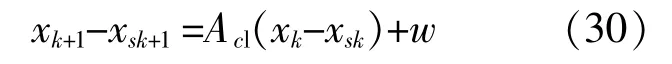
根据送端电网暂态能量平衡控制优化问题中的假设，在实时N个时刻的预测控制后，采取反馈控制Δu=K（x-xs），则k+1时刻送端电网暂态能量平衡控制的一组可行功的机组切机量控制策略为

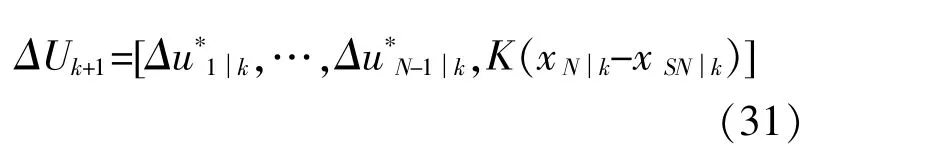
4 算例分析

以河北某电厂送出案例对本文所提出方法进行验证。采用PSD-BPA机电暂态仿真软件构建如图3所示的单厂送出系统。都上都电厂通过三回线输电通道接入受端系统。

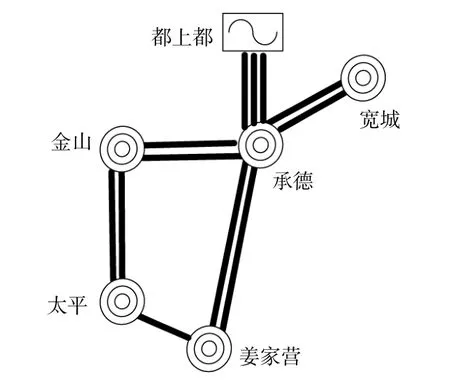
图3 都上都电厂送出系统结构图Fig.3 The structure diagram of the transmission system of the Dushangdu power plant

电网等值确定了电网暂态能量模型，因此在PSD-BPA机电暂态仿真平台中须要校验等值电网的正确性。表1给出了都上都电厂送出系统潮流参数。

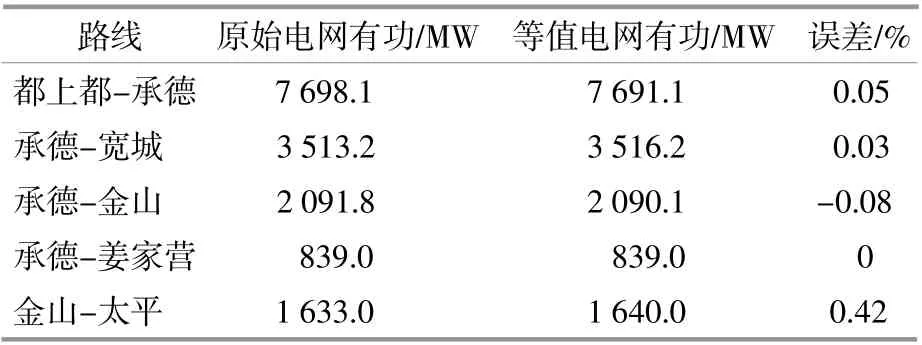
表1 都上都电厂送出系统参数Table 1 Duhangdu power plant transmission system parameters

在不同情况下，系统控制前后的电压波形如图4、图5所示。系统无功波动情况如图6所示。控制后频率波动情况如图7所示。

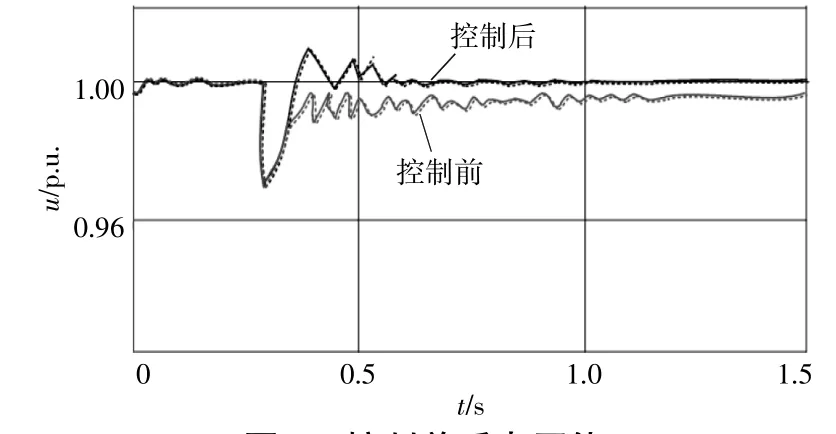
图4 控制前后电压值Fig.4 Voltage value before and after control

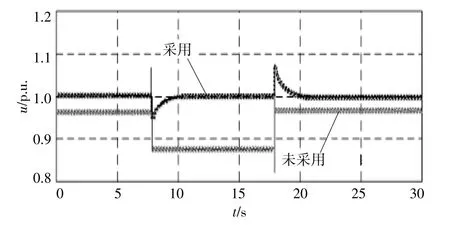
图5 动态控制电压仿真结果Fig.5 Dynamic control voltage simulation result

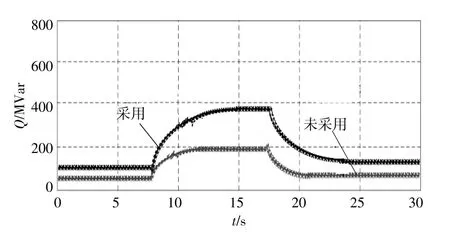
图6 动态控制无功仿真结果Fig.6 Dynamic control reactive power simulation results

图7 控制后频率波动情况Fig.7 Frequency fluctuation after control

图8为系统控制前后的功角特性曲线。分析控制前后系统的功角特性曲线可知，在A1>A2时系统失稳，此时须采取安控措施。设控制措施为切机，切机量为ΔPd。基于等面积定则，机组加速面积等于机组减速面积。通过以上分析可得，采用多能源送端电网暂态能量平衡快速鲁棒控制后，通过调节热网和气网的管道压力，使故障期间的转子加速能量减小。故障切除后，转动惯量越大，故障切除角越小，机组减速能量越大，切机量也相应减小，可以减少在电力系统故障情况下的切机容量。

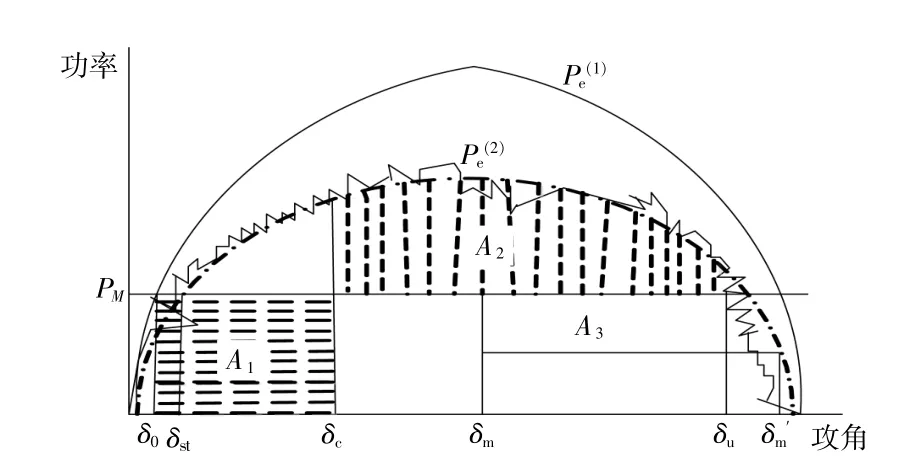
图8 控制后系统功角特性曲线Fig.8 System power angle characteristic curve after control

5 结论

本文所提出的送端电网暂态能量动力学模型，能够较好地反映送端系统暂态过程中的系统惯性参数、功率控制系统时间延迟参数和等值电源转子运动参数间的非线性对应关系。

考虑可再生能源、多源储能和多能源负荷接入后送端电网阻尼的时变特性及其变化的确定性，提出了送端电网暂态功率鲁棒控制器模型，能够有效兼顾实时功率控制过程中的控制量最优解的鲁棒性问题。

针对单厂送出和送端电网算例的仿真结果表明，本文提出的送端系统暂态能量控制模型，在功率控制精度和实时控制时效方面具有较好的性能。