基于优化小波重构算法的直流输电线路故障测距方法

刘政,张蔚,季小雨,陈炯

（1.上海电力大学，上海 200082；2.国网上海电力公司松江供电公司，上海 201600；3.国网浙江长兴县供电公司，浙江湖州 313100）

0 引言

随着全球能源互联网战略的实施，我国风电、光伏等可再生能源的占比不断提高[1]。面对可再生能源日益增长的输送需求，直流电网的建设方兴未艾，柔性直流输电技术（HVDC-Flexible）被广泛地应用。当输电线路发生故障时，直流断路器动作，切除故障，整条线路退出运行，会降低输电能力。因此，在线路故障发生后，快速判断故障发生位置并予以排除，是一项重点研究课题。

文献[2]对发生故障的输电线路两侧行波传输模型进行分析表明，交流线路发生故障时，行波测距法可以有效地依靠电压波形的变化确定故障位置，但未对直流线路故障情况加以详细分析。文献[3]提出了一种基于多尺度模糊熵的高压直流输电线路的故障识别方法，用色散理论解释了波的传递过程，但对提高识别灵敏度的研究不充分、不完全。文献[4]从直流配电网的角度出发，基于Floyd算法搜索各节点间的最短路径距离矩阵，可以有效判断故障发生的区间，但精度不高，不适用于高电压、长距离的直流线路故障测距。文献[5]提出了将小波变换作为行波识别的工具，在电缆故障的测距中实现了高精度定位，但未对小波重构的阈值设置加以详细说明；当故障发生在直流架空线路时，检测的灵敏度大大降低，不利于在工程中的大规模应用。

综上所述，虽然目前对于直流线路故障行波测距的研究较多，但对于直流架空线路发生故障时的故障定位问题尚缺少普适性的研究成果。特别是针对行波测距中，提高行波波头识别灵敏度的问题须要加以深入研究。

本文以直流架空线路故障定位的实际工程为背景，提出了直流架空线路故障测距模型及其基于优化小波重构算法的直流输电线路故障行波测距方法。仿真结果表明，基于优化小波重构算法的直流线路故障测距方法，可以显著提高直流线路故障定位的精度和灵敏度，具有广泛的应用价值。

1 行波测距的原理和模型

直流架空线是电能传输的通道，在故障发生后，线路上的电气量发生突变，由于输电距离长，故障波会向线路两侧传播。随着行波传输至两侧，反射波也会以能量递减的形式在故障区间不断传递（图1）。图中：RF为接地电阻；-UF为接地故障时线路对地等效电动势；iF为对地故障电流；u1，u2，u3，ur为故障电压行波；il，ir为故障电流行波。

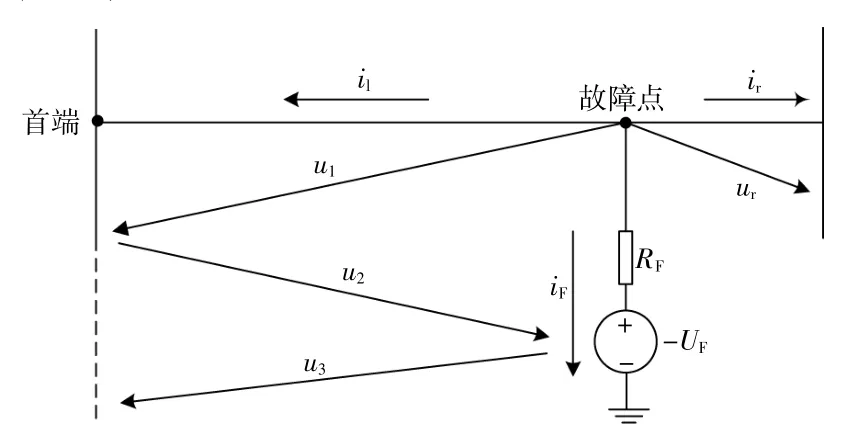
图1 故障行波的传播Fig.1 Propagation of fault traveling wave

设线路的波阻抗为Z，则有：

由式（3）可见，ueq是典型的指数函数。在对指数函数进行小波分解后，可得到一同等幅值冲击函数，更加易于识别故障行波波头出现的位置。故小波分解适合应用于直流线路故障行波的检测识别中。

单端行波测距的原理如图2所示。

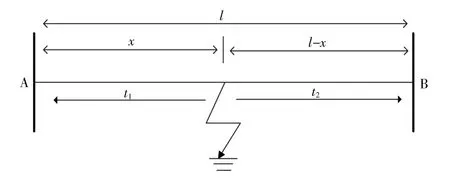
图2 行波测距的原理图Fig.2 Schematic diagram of traveling wave ranging

图中：l为直流线路首末端A，B之间的距离；x为A至故障点的线路长度；t1为故障行波第一次传到A点的时刻；t2为故障行波经A点反射后再次被故障点反射时，A点接收到行波的时刻。

由安装于A，B点的检测装置记录行波波头出现的时间并计算x：

式中：υ为波速，其大小与线路的参数无关，仅取决于线路架设外界环境的介电常数。

实际应用中，由于故障波速度极快，线路两端检测装置的高频录波器在极短时间内记录的波形不会发生突变，因此必须予以处理才能准确地识别行波波头到达的位置。

2 小波变换法在行波波头识别中的应用

行波波头的识别本质上是研究波形出现梯度最大点的时刻，对于一段时域内的波形，可以通过小波变换绘制出它的时频波形。时频图中频率幅值最高的点就是波形发生畸变的时刻。小波变换非常适用于行波波头的识别分析。

实际工程中，换流器阀的动作带来高次谐波，而且由长距离架空线的分布特性所决定，直流线路上传输的电气量必然带有噪声。传统的小波变换重构时，将大量的噪声波形误判为故障波，造成识别精度降低。因此，特别需要一种适于工程实际的小波重构算法来解决此问题。

小波变换处理波形通常分为3步。第一步是根据波形的特征选取适合的小波函数；第二步是设置采样尺度并进行小波分解；第三步是设置阈值，过滤掉噪声信息进行小波重构，得到模极大值。

本文选取香农小波作为故障波分解的小波函数。设采样间隔时间为d，在第j个层级的尺度空间采样，采样间隔为d/2j（j为正整数）。

对函数f（t）在区间[a，b]上采样时，采样点见式（4），采样值见式（5）：

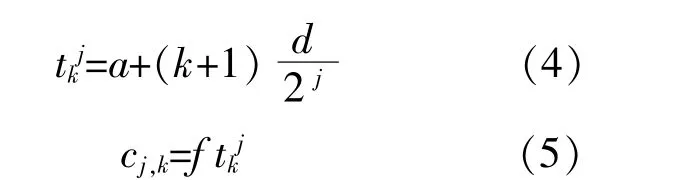
式中：k为位移系数（k为正整数）；cj，k为小波重构的逼近系数。对于第j层的逼近，若φ是赋范线性空间Vj上的一个小波基，φj，k（t）是它的一组伸缩和平移变换，则：

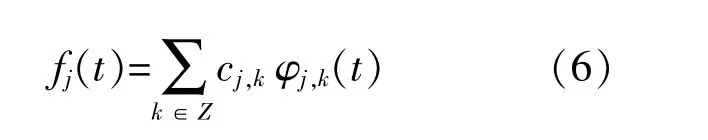
fj（t）是在第j层空间Vj上的一个对函数f（t）的近似。在小波重构算法中，通过逼近系数描述了第j层的逼近fj（t）。Vj由φj，k（t）作为基生成。将逼近值与实际值的差值记为ωj（t），则有：

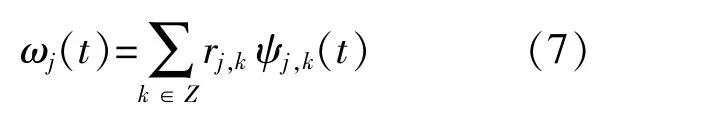
式中：rj，k为细节系数；ψ为小波基φ在该赋范线性空间上唯一对应的正交小波基。

利用高一层的逼近系数cj+1，k和本层的双尺度系数hk，gk，计算本层的逼近细数cj+1，k和细节系数rj，k，实现分解过程：

根据实际情况设定分解的层数。逼近分量fj（t）与细节分量ωj（t），满足关系fj+1（t）=fj（t）+ωj（t），故可求解至精度满足分解需要的赋范线性空间层，获得信号f（t）的最优逼近分解fJ（t）。

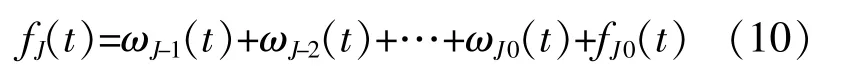
式中：J为小波分解的层数（J为正整数），通常只须要进行一层小波分解（即J=1），即可有效地识别信号；fJ0（t）是函数f（t）的初始近似分解，故为信号f（t）的小波分解。

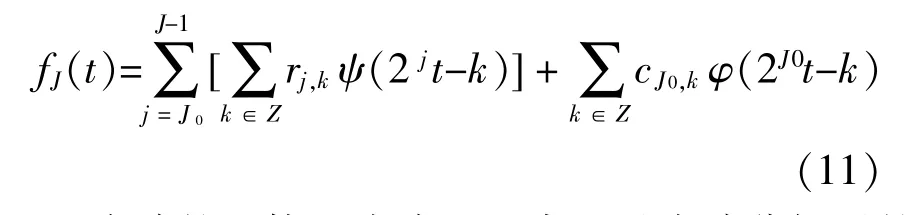
小波的重构即为式（11）中经过小波分解后的fJ（t）选择适合的小波细节系数，以滤除干扰信号。一般地，采用多氏小波系数估计法来确定细节系数阈值的大小[6]：

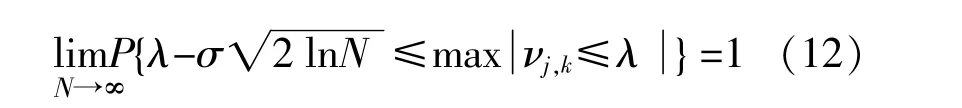
式中：σ为噪声信号的标准差；N为采样点个数，为正整数；λ是阈值，当小波系数小于此阈值时，在重构过程中将此系数置零，否则系数不变；νj，k是小波系数的幅值。

对理想情况下0.01 s产生的故障电流波形进行一层小波分解，得到小波分解波形如图3所示[5]。图3中，cd1为经过一层小波变换后的小波模值大小，取模极大值为行波波头的到达时刻。在实际工程中，经过小波分解原理得到的cd1是离散的，因此只须要寻找cd1的最大模值，就可以根据其对应的出现时间，判断行波波头的到达时刻。

在第一部分，中由于分段logistic映射的初值取值范围和chebyshev映射的初值范围相同,所以选用分段logistic映射的输出来控制chebyshev映射的初值,为增加序列的不可预测性,用chebyshev映射的输出反控制分段logistic映射的初值,给定分段logistic映射初值为0.76,系统参数为2。

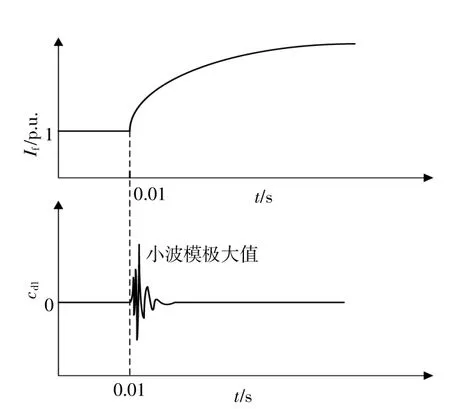
图3 故障电流波形及小波变换后的时频波形图Fig.3 Fault current waveform and time frequency waveform after wavelet transform

通过小波变换的时频图可以将识别波形畸变点的问题转换为识别cd1极大值的问题。准确地判断行波传输到线路一端的时刻t1，t2，并由式（3）计算故障位置，实现直流线路的故障测距。

3 基于弹性阈值选取的优化小波重构算法

由式（13）可看出，传统小波重构法中的小波细节系数ωj，k不连续，会造成边缘效应，影响故障行波的识别精度。本文根据已有的研究结论，基于香农函数，提出了改进的平滑系数重构法：

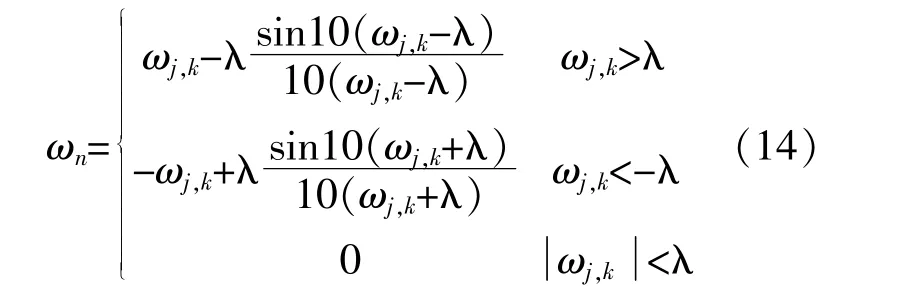
式（14）的系数重构法原理如图4所示。此系数设置方法可以快速逼近参考系数值，且处处连续。

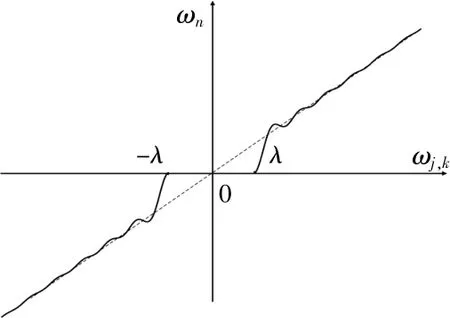
图4 改进小波系数重构法的原理图Fig.4 Schematic diagram of improved wavelet coefficient reconstruction method

4 算例分析

以直流输电线路单极接地故障为例，验证基于优化小波重构算法的直流输电线路故障行波测距方法的有效性。同时，设置多种类型的故障，比较该方法在各种故障测距中的精准度。

4.1 单极接地故障时的测距效果仿真分析

以真双极、极间电压20 kV、长度100 km的贝瑞隆架空线模型为例验证方法的准确性。设0 s起系统开始运行；1 s时，在线路距离A点40 km处发生单极线接地故障。端口的采样装置采样间隔为2μs，端口检测装置记录的电流波形如图5所示[8]，[9]。对电流波形进行小波分解，得到每个时刻对应的一层小波系数cd1；绘制传统方法和弹性阈值法下的小波分解时频图如图6所示。

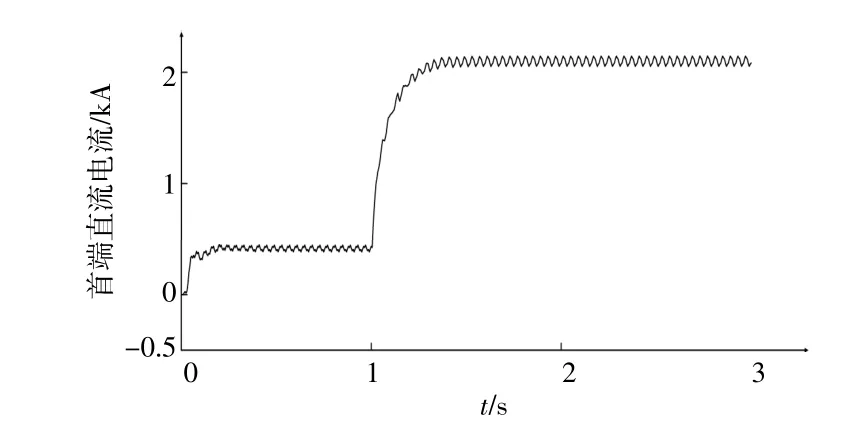
图5 故障后直流线路一端电流检测装置记录的电流波形Fig.5 Current waveform recorded by current detection device at one end of DC line after fault

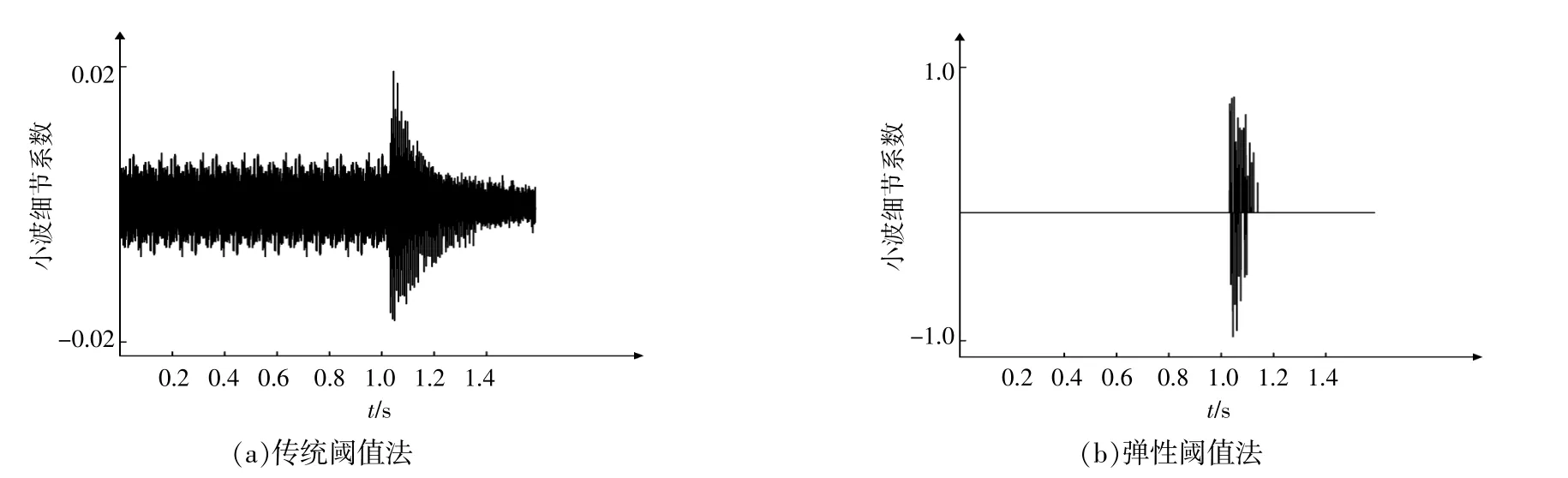
图6 两种阈值法下故障电流的小波细节系数分布图Fig.6 Wavelet detail coefficient distribution of fault current based on two threshold methods

由图6可以看出，采用弹性阈值选取方法时，故障电流的细节系数更加清晰，更有利于行波波头的识别。以出现第一个非零小波模值对应的时间作为行波传递到首端的时刻观察，第一个出现的非零小波模值并不是小波的模极大值。这是因为采用改进的小波重构算法，在ωj，k趋近于阈值时，对应的ωn值会比实际值略小。因此，采用第一个非零小波模值的出现时间，来判断故障行波的到达时间是合理的。

4.2 暂态稳定控制策略响应特性仿真分析

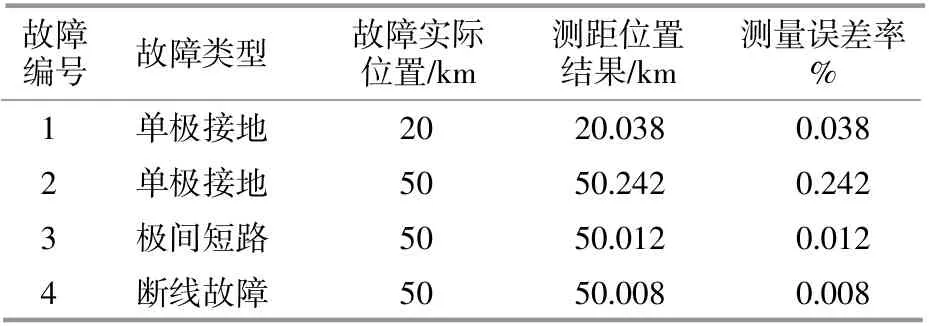
表1 不同故障情况下的故障测距结果Table 1 Fault location results under different fault conditions

从表1中可以看出，优化后的行波故障测距法可以快速、准确地检测出故障点到线路首端、末端的距离，具有较高的精度。在所有故障中，断线故障测距的准确度最高；故障越靠近线路中间点，误差越小。这是因为与短路故障相比，断线故障在故障前后的电流变化最大，易于识别。由于极间短路的电流大于单极接地故障下的电流，极间短路故障的测距结果精度更高。

5 结论

直流线路发生故障时，根据行波在线路首、末端之间的传输特点，利用两端行波波头到达的时间测定故障发生的位置；提出了一种基于改进小波重构算法的故障行波测距法，使直流线路故障的测距具有较高的精度。

基于行波波头典型的指数衰减特征和直流故障发展速度快的特点，利用小波分解作为波头识别的手段，并给出了传统小波重构过程中硬阈值法的原理。

针对已有的阈值选取方法不连续的问题，提出了基于香农函数衰减特征的小波系数重构法，新构造的小波重构模型处处连续，且在小波细节系数大于阈值后，快速逼近实际值，具有良好的特性。

本文以仿真算例验证了在单极短路、极间短路和断线故障下进行故障测距的有效性，表明该方法具有工程实际应用的潜力。