双馈机群次同步谐振聚合建模与分析

2021-12-28王丹贾祺胡文波王俊茜刘侃李德鑫

可再生能源 2021年12期

王丹,贾祺,胡文波,王俊茜,刘侃,李德鑫

（1.现代电力系统仿真控制与绿色电能技术教育部重点实验室（东北电力大学），吉林吉林 132000；2.国网吉林省电力科学研究院，吉林长春 130021）

0 引言

大规模开发利用风能是我国能源战略的重要组成部分，截至2020年底，我国风电累计装机容量达2.81亿kW，预计到2050年，风电装机容量将达到24亿kW。其中大多数风电机群离负荷中心较远，串联补偿技术在风电大容量、远距离输送中得到了广泛应用，但同时存在诱发次同步谐振（SubSynchronous Resonance，SSR）的风险[1]。

国内外已发生多起双馈机群SSR事故[2]，[3]。针对双馈机群与串补线路之间的SSR问题，国内外学者通过特征值分析、阻抗分析、时域仿真等方法分析了其产生机理和影响因素。研究结果表明：双馈串补系统SSR的机理为控制系统参与的感应发电机效应[4]，[5]，发生振荡时，谐振频率下双馈机群的等效电阻变成负值，当这一负电阻超过电网电阻时，次同步频率电流将会持续存在并增大；主要影响因素为风速、串补度、风机台数以及转子侧变流器内环比例系数Kp[6]，[7]，其中，风速、串补度、Kp与系统稳定性呈线性关系，风速越高、串补度及Kp越小系统稳定性越强，风机台数与系统稳定性呈非线性关系；不同位置的风机对系统的SSR特性影响程度不同[8]。

风电机群详细模型维度过高且仿真困难，已有研究大多采用等值模型表征风电机群。常用的等值建模方法为单机等值法和分群聚合法[9]，[10]。文献[11]，[12]提出了风电机群等值模型的准确度评价方法，在稳态、突变风速、故障条件下对分群聚合模型进行准确性评价。现有对于聚合模型的评价大多关注扰动下聚合模型的功角稳定问题，少有文献研究SSR条件下分群聚合模型的主导振荡特性保持能力。

本文阐述了双馈机群串补系统中聚合模型的建模方法，并在PSCAD/EMTDC平台上，搭建了双馈机群详细模型、分群聚合模型及单机模型。基于SSR常用的时域仿真法、特征值分析法、阻抗分析法，综合分析了不同并网台数、集电线路参数条件下3种模型的SSR特性，对SSR下聚合模型的适用性进行了验证。

1 系统结构

图1为双馈风电机群经串补并网系统结构图，风电机群先经过0.69/35 kV，35/220 kV变压器升压后呈辐射状连接至并网点，然后经220/500 kV变压器再次升压，最后通过串联补偿线路接入500 kV系统。图中：Rg，Lg，Cg分别为输电线路的电阻、电感和串补电容；Lc为风电机群与并网点之间的线路电感。为简化分析，本文假定风电机群可根据运行工况分为7组，各组风机负荷特性、控制参数完全相同，可用单台机组进行等效，单机额定容量为1.5 MW。

图1 双馈风电机群经串补并网系统结构图Fig.1 Structure of DFIG group series-compensated gridconnected system

2 双馈机群聚合模型

分群聚合模型是在考虑机群内风电机组运行工况差异性的条件下，按照一定的准则对风电机组进行分群，常用分群准则为风速/转速相近。本文采用k-means聚类算法[13]，以输出有功功率的相似度作为分群指标，并基于手肘法对分群数k进行选取，“肘部”对应的k值即为真实聚类分群数。其他参数聚合方法如下。

2.1 等值输入风速

风力机机械功率为

式中：ρ为空气密度；A为风力机叶片扫略面积；Cp为风能利用系数；v为风速。

聚合后的风机须等效代替同群中n台风机机械功率之和，设所有风力机参数相同并都能实现最大风能捕获，即Cp=Cpmax，则风机聚合模型输出功率为

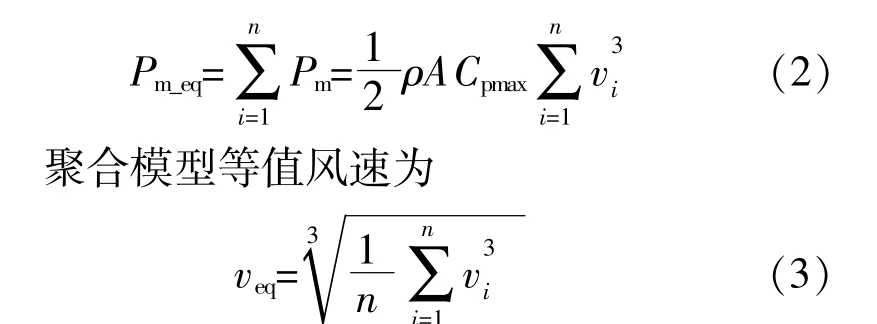
2.2 等值异步电机

等效风机的容量Seq等于同群中所有风电机组容量之和，相应的，等值有功功率Peq、无功功率Qeq也等于同群中所有风电机组之和。聚合后的风电机组转子转速ωr_eq可由风机的风速-转速曲线得到，转速范围与单台机组相同，均为0.67ω0～1.2 ω0，其中ω0为定子角频率。等值模型机械转矩Tm_eq和电磁转矩Te_eq表达式分别为

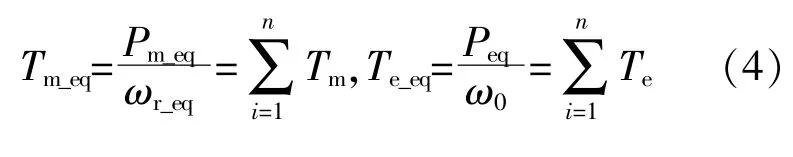
2.3 轴系

双馈机群串补并网系统中轴系固有频率一般为1～3 Hz，所需引起次同步扭振相互作用的串补度较高，因此发生次同步谐振时一般不会发生轴系扭振，建模时可忽略轴系扭振，建立单质量块模型。

式中：Tji为第i台机组的惯性时间常数。

2.4 控制系统

控制系统中的电流跟踪控制环采用双闭环控制。其中：转子侧变流器（Rotor-Side Converter，RSC）根据风速调节转子转速，并保持发电机定子不输出无功功率；网侧变流器（Grid-Side Converter，GSC）保持直流电压和定子机端电压恒定，详细控制框图见文献[4]。

以RSC为例分析聚合模型控制参数，RSC的数学模型为式

中：urdref，urqref分别为d，q轴RSC输出电压参考值；Kpω，KpQ分别为d，q轴RSC外环比例积分系数；ωr，ωrref分别为转子转速实际值、参考值；Qs，Qsref分别为定子无功功率实际值、参考值；ird，irq分别为d，q轴RSC输出电流；Kpm，Kim为RSC内环比例积分系数。

聚合后等值风机转速与转速参考值范围不变，电压量保持不变，无功功率、电流量随容量的增加而增加，则聚合模型控制系统电气量表达式如下：

为保证聚合后控制系统量级的一致性，聚合模型与单台机组RSC控制参数之间的关系为

式中：Kpiω，KpiQ分别为d，q轴RSC外环比例积分系数；Kpim为RSC内环比例积分系数。

聚合模型与单台机组GSC控制参数之间的关系为

式中：Kpiudc，Kpiut分别为d，q轴GSC外环比例积分系数；Kpig为GSC内环比例积分系数。

2.5 等值参数

基于聚合模型和同群内单台机组的电压电流关系，聚合模型的等值电气参数在数值上等于同群内所有风机并联后的值。

式中：Req，Leq，Ceq分别为聚合后风机的定转子电阻、电感、变流器直流电容；Ri，Li，Ci分别为聚合前风机的定转子电阻、电感（包括定转子电感、励磁电感、变流器连接电感）、变流器直流电容。

3 有效性评价方法

SSR常用研究方法为阻抗法、特征值分析法、时域仿真法、负转矩系数分析法等。为分析SSR下聚合模型的有效性，本文从3个方面进行综合评价：①基于时域仿真法分析聚合模型和详细模型输出有功功率的波形相似度；②建立线性化模型，对比分析聚合模型和详细模型的主导振荡特征根；③建立阻抗模型，对谐振频率下聚合模型和详细模型的等效电阻进行定量分析。由于现有双馈机群SSR研究常用模型为单机模型，故本文同时对单机模型和聚合模型进行对比分析。

3.1 线性化建模

本文采用特征根分析法对详细模型和聚合模型的SSR特性进行对比，即建立系统的线性化模型并求解其系数矩阵的特征值，进而判断动态系统的小干扰稳定性。

双馈机群经串补并网系统线性化模型结构如图2所示。采用分块建模的思想，对双馈风机中轴系、感应电机、RSC、GSC控制系统、直流电容各部分以及电网进行分块建模，将各模块根据输入输出关系进行连接，其中，双馈风机向电网输出电流量，电网对每个风机输出电压量，构成闭环系统。

图2 双馈机群经串补系统线性化模型结构Fig.2 Structure of linearization model of DFIG group series compensation system

在稳态运行点处线性化，消去中间变量，得到整个系统模型为

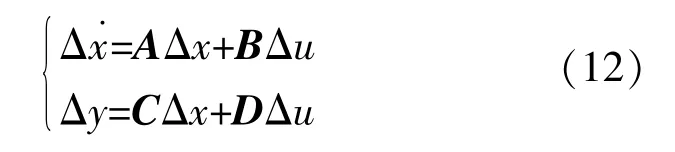
式中：Δx˙为状态变量；Δu为输入量；Δy为输出量；A，B，C，D为状态矩阵。

系统稳定性与A矩阵的特征根有关，其中，特征值的实部表征系统的发散速度，虚部可以计算出系统的振荡频率。聚合模型与详细模型在次同步频段内对应的特征根越接近，聚合模型越能准确表达机群主导振荡特性。

3.2 阻抗建模

发生SSR时，由于滑差和控制系统的共同作用，在次同步频率下转子侧等效电阻为负值，当风机等值负电阻大于线路电阻时，系统振荡失稳。双馈风机等效电路图如图3所示。图中：Rs，Rr分别为定、转子电阻；Ls，Lr分别为定、转子漏感；Lm为励磁电感；Ursc，Zrsc分别为RSC控制系统等效电压、阻抗。

图3 双馈风机等效电路图Fig.3 Equivalent circuit of DFIG

由于RSC内环对SSR特性影响较大，阻抗建模时控制系统可只考虑RSC电流内环（Kpim）。采用空间矢量法进行建模[14]，RSC内环控制系统复频域表达式为

式中：H（s）为RSC电流内环PI控制环节；Kd为交叉耦合项；urdref，urqref分别为d，q轴RSC输出电压参考值。

复频域下考虑RSC内环控制系统的双馈风机阻抗模型为

通过计算振荡频率下双馈机群及系统等效电阻，可对聚合模型的有效性和准确性进行评价。

4 仿真算例

在EMTDC/PSCAD中搭建图1所示系统的详细模型、聚合模型和单机模型，其中，风力机的风能捕获特性如图4所示，双馈风机参数见表1。

图4 风力机风能捕获特性Fig.4 Wind energy capture characteristics of wind turbine

表1 双馈风机参数Table 1 Parameter of DFIG

7组风机的运行工况分别为4，4.2，6.3，6.4，6.4 6，8.5 ，8.8 m/s。6 s时投入串补，串补度为6.6 7%，改变RSC内环比例积分系数Kp，对聚合模型有效性进行分析。

4.1 不考虑台数和集电线路差异

当7组双馈风机并网台数相同（各100台）、集电线路完全相同时，根据手肘法，聚合模型可分为3群，等效运行工况分别为4.1，6.387，8.653 m/s；单机模型运行工况为6.815 m/s。设置RSC的Kp分别为0.015，0.15，3种模型输出有功功率如图5所示。

图5 Kp变化时3种模型输出功率Fig.5 3 models output power when Kp changes

从图5可以看出：6 s投入串补后，Kp=0.015时系统稳定运行，Kp=0.15时系统发生振荡，聚合模型与详细模型的有功功率波动趋势基本一致，振荡时单机模型振荡频率略小；Kp分别为0.015，0.1 5时，聚合模型与详细模型输出有功功率P分别相差0.2 MW，0.0 9 MW，误差率小于0.0 7%，且精确度高于单机模型。

Kp从0.015变化到0.15时，3种模型的主导振荡特征根结果如图6所示。

图6 特征根分析结果Fig.6 Results of characteristic root analysis

图6中：随着Kp的增大，详细模型特征根由负变正，详细模型与两种等值模型都反映了这种变化趋势，且聚合模型准确度高于单机模型；Kp从0.015变化到0.15时，两种等值模型的特征根实部偏差增大，准确性降低，其中聚合模型特征根实部偏差为0～0.09，误差率小于2%；聚合模型、详细模型振荡频率近似相同，约为7 Hz，单机模型振荡频率略小（约0.16 Hz），与仿真分析结果一致。

Kp=0.15时，振荡频率下等值模型与详细模型220 kV侧系统等效电阻如图7所示。

图7 Kp=0.15时系统等效电阻Fig.7 The equivalent resistances when Kp=0.15

图7中：随着f的增大，220 kV侧系统等效电阻由正到负，系统趋于不稳定，详细模型和两种等值模型都反映了这种变化趋势，且聚合模型准确度高于单机模型，与特征根分析结果一致；振荡频率下（约6.52 Hz），详细模型系统等效电阻为-2.108Ω，聚合模型等效电阻误差约为0.007Ω，误差约为详细模型的0.3%。

4.2 考虑机组台数差异

当7组双馈风机并网台数不同时，设置机组1～7的台数分别为150，150，100，100，100，50，50台，聚合模型等效运行工况不变，单机模型运行工况变为6.16 m/s。

投入串补后，聚合模型与详细模型的有功功率波动趋势基本一致，振荡时单机模型振荡频率略小。RSC的Kp为0.015，0.15时，聚合模型与详细模型输出有功功率分别相差约0.1 MW，0.15 MW，误差率小于0.07%，且精确度高于单机模型。风机台数不同时聚合模型有功功率误差率基本不变。

Kp从0.015变化到0.15时，3种模型的主导振荡特征根结果如图8所示。图中：随着Kp的增大，两种等值模型与详细模型特征根变化趋势相同，且聚合模型准确度高于单机模型；Kp从0.015变化到0.15时，聚合模型特征根实部偏差为0～0.1 1，误差率小于2%；聚合模型、详细模型振荡频率近似相同，单机模型振荡频率略小（约0.1 6 Hz）。考虑机组台数差异性后，聚合模型的主导振荡特征根准确性变化不大。

图8 特征根分析结果Fig.8 Results of characteristic root analysis

Kp=0.15时，振荡频率下等值模型与详细模型220 kV侧系统等效电阻如图9所示。

图9 Kp=0.15时系统等效电阻Fig.9 The equivalent resistances when Kp=0.15

图9中：随着f的增大，详细模型和两种等值模型系统等效电阻变化趋势相同，且聚合模型准确度高于单机模型，与特征根分析结果一致；振荡频率下（约6.05 Hz），聚合模型等效电阻误差约为0.0 06Ω，误差率小于详细模型的0.4 %。考虑机组台数差异性后，聚合模型等效电阻误差率变化不大。

4.3 考虑集电线路差异

当7组双馈风机并网台数相同、集电线路阻抗不同时，设置机组1～7的集电线路长度分别为100，200，300，400，500，600，700 m，运用等功率损耗法对聚合模型、单机模型的集电网络进行等值，即等效前后集电线路功率损耗基本相同。

投入串补后，等值模型与详细模型的有功功率波动趋势基本一致，单机模型振荡频率略小。RSC的Kp为0.015，0.15时，聚合模型与详细模型输出有功功率分别相差约0.2 MW，0.1 MW，误差率小于0.07%，且精确度高于单机模型。集电线路阻抗不同时，聚合模型有功功率误差率基本不变。

Kp从0.015变化到0.15时，3种模型的主导振荡特征根结果如图10所示。

图10 特征根分析结果Fig.10 Results of characteristic root analysis

图10中：随着Kp的增大，两种等值模型与详细模型特征根变化趋势相同，且聚合模型准确度高于单机模型；Kp从0.015变化到0.15时，聚合模型特征根实部偏差为0～0.21，误差率小于3.5%；聚合模型、详细模型振荡频率近似相同，单机模型振荡频率略小（约0.3 2 Hz）。考虑集电线路差异性后，聚合模型主导振荡特征根实部偏差略增大，单机模型振荡频率偏差增大。

Kp=0.15时，振荡频率下等值模型与详细模型220 kV侧系统等效电阻如图11所示。