Mn掺杂6H-SiC的第一性原理研究

王熠欣， 谢 泉， 邹 江

(贵州大学 大数据与信息工程学院 新型光电子材料与技术研究所， 贵阳550025)

1 引 言

碳化硅(SiC)是一种第三代宽禁带半导体，在高功率和高温设备中具有强大的潜在应用[1]. 作为一种稀释磁性半导体，由于其在高温高频设备中具有巨大潜力，已经成为稀磁半导体的主要研究方向. 该材料物理结构与光学性质优异，具有禁带宽度大，饱和电子漂移率高，抗击穿电场强度高等特点，现已成为新型半导体材料的研究热点之一[2].

许多研究者使用第一性原理方法或实验方法研究了不同构型的SiC的性质：黄毅华[3]等使用DFT方法研究了Al掺杂6H-SiC的电子结构与磁性性质，在Al及Si空位共掺杂后体系出现明显磁性. Gao等人[4]用实验方法制备6H-SiC纳米线，观察到Al掺杂剂引起光致发光带的红移. 林龙等[5]用N掺杂6H-SiC探究了其电子结构与磁性性质，Si空位掺杂后出现反铁磁性. 杨昆等[6]，用实验方法(物理气相沉积PVD)Ti掺杂研究电阻率等电学性质. 史茹倩等[7]通过密度泛函理论计算P掺杂4H-SiC超晶胞电子结构. 邹江等[8]对稀土元素(Ce、La)掺杂6H-SiC的电子结构和光学性质做了密度泛函理论计算分析. Azri等人[9]使用第一性原理计算了Mn掺杂6H-SiC的电子结构与磁性性质，提出在以Mn替代Si位或C位时掺杂系统中产生具有不同值的净磁矩. 但以上研究中对Mn掺杂的6H-SiC作为半导体的能带性质，以及掺杂后的光学性质的改变未作出详细分析. 故本文使用密度泛函理论(DFT)方法，对Mn替位Si掺杂6H-SiC的电子结构与光学性质做研究分析，探究在Mn元素掺杂后对6H-SiC性质的影响，期望Mn的掺杂可以改善6H-SiC的电子结构及光学性能，为此材料在微电子和光电子器件中的应用提供理论依据.

2 模型构建与计算方法

SiC有多种同质异形体，本次计算使用6H-SiC构型，其中6H含义为6个原子层周期性堆垛，堆垛形式为“ABCACB”. SiC结构稳定，每个C原子与4个Si原子以共价键相结合. 计算使用的6H-SiC的空间群为P63mc，常温常压下，6H-SiC具有六角晶系结构，其晶格常数为a=b=3.08 Å，c=15.19 Å.α=β= 90°，γ= 120°[10]. 计算使用的结构为2×2×1超胞，如图1(a)所示. 掺杂方式使用替位式掺杂，Mn原子替换晶体结构中一个Si原子的位置，掺杂后的超胞如图1(b). 掺杂前分子式为Si43C34，掺杂后为MnSi42C34，杂质浓度超过1.0×1018cm-3，属于重掺杂情形[11].

本次计算使用Materials Studio软件的CASTEP软件包进行密度泛函理论计算[12]，是一种从头算的量子力学方法[13]. 计算使用广义梯度近似GGA加PBE泛函. 在经过截断能(Energy cutoff)与K点网格(K-point net)的一系列收敛性测试之后，将截断能量设置为420 eV，K点网格设置为3×3×1用于结构优化，自洽场计算中迭代能量收敛梯度设定为2.0×10-6eV/atom-1，将原子核与核外电子的赝势设定为超软赝势(OTFG-ultrasoft)[14]. 掺杂的6H-SiC的价电子构型为Si：3s23p2，C：2s22p2，Mn：3d54s2. 计算过程首先对扩大后的超胞进行几何结构优化，再分别进行电子结构与态密度计算，最后计算光学性质. 计算在倒易空间中进行.

图1 6H-SiC与Mn掺杂的6H-SiC的晶体结构模型Fig. 1 Crystal structures models of 6H-SiC and Mn-doped 6H-SiC

3 结果与分析

3.1 几何结构分析

未掺杂的6H-SiC超胞与Mn掺杂后的6H-SiC超胞在几何优化后，自洽精度和系统能量收敛完成，收敛参数小于设定标准值. 表1显示了晶胞的晶格参数(lattice parameters)，体积(cell volumes)，总能量(ET). 几何优化后结果与实验值误差较小[15]. 这也表明了基于DFT的第一性原理计算的可靠性.

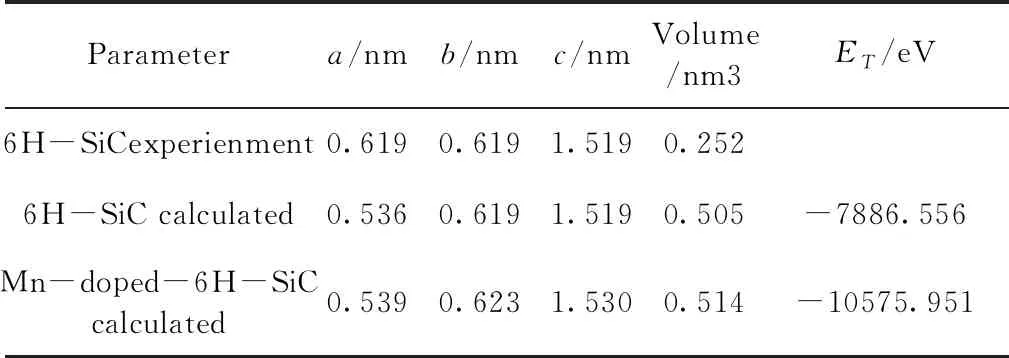
表1 掺杂前后超胞的晶格常数、晶胞体积以及总能量(ET)

比较表1中的相关数据，发现6H-SiC的晶格常数随Mn原子的添加变化非常小，掺杂后体系改变较小. 从原子半径的角度解释，所掺杂元素Mn的原子半径(0.179 nm)相较于Si原子的半径(0.117 nm)大，当Mn原子取代Si原子时， c方向晶格常数有扩大. 6H-SiC结构较为稳定，当Mn元素掺入后，Mn离子多余的正电荷在库仑排斥力的作用下，晶格发生膨胀，从而导致晶胞体积的增加. 从能量角度看，未掺杂的6H-SiC的体系总能量为 - 7886.556 eV，相较于掺杂后的体系的 - 10575.951 eV小，所以未掺杂的结构比Mn掺杂后的结构更加稳定.

3.2 能带结构

为了更好地分析和研究Mn掺杂后的6H-SiC电子结构，进一步计算了能带结构. 定义费米能级设在价带顶0 eV处.

如图2(a)中，选取G、F、Q、Z、G点为第一布里渊区的高对称点，观察未掺杂状态的6H-SiC的能带状态图可以发现，价带能量最高点与导带能量最低点分别位于布里渊区的Z点和G点，未在同一布里渊区高对称点内，为间接带隙半导体. 禁带宽度Eg约为2.022 eV，相较于实验值(Eg=2.039 eV)低，可能是由于广义梯度近似(GGA)计算方法低估带隙所致[16].

图2(b)为Mn原子掺杂后的能带结构图，由于 - 20 eV以下能带结构离费米能级较远，对电子跃迁分析作用相关性不大，故略去掺杂后体系 - 20 eV以下能带结构. 在Mn原子掺杂后价带与导带均有所展宽且其向费米能级处移动，价带能量最高点与导带能量最低点分别位于布里渊区的Q点和G点，以致禁带宽度Eg降低为0.602 eV. 在Mn原子替位式掺杂Si后，Mn原子成为受主杂质，价带顶跨过费米能级，6H-SiC成为p型半导体. 比较掺杂前后的能带结构图可以发现，Mn的掺入为6H-SiC在原有价带能级底部处引入新的受主能级，且在掺杂后能级变得更加致密.

为深入探究能带中各能级特征，对Mn掺杂的6H-SiC进行了马利肯布居数分析(Mulliken’s population analysis). 表2中列出了部分元素成键的典型值，C与Si由于最外层电子结构稳定，达到电子饱和状态，重叠布居数接近1，说明掺Mn的6H-SiC中C与Si依旧以共价键方式结合. 而替位Si而掺杂进入的Mn原子与周围C原子的重叠布居数近似为0，故分析可能Mn原子并未与周围C原子成键而单独存在于6H-SiC体系中.

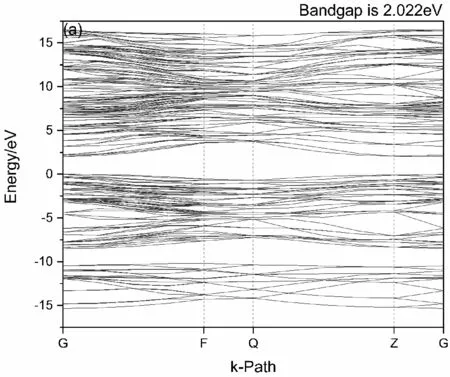
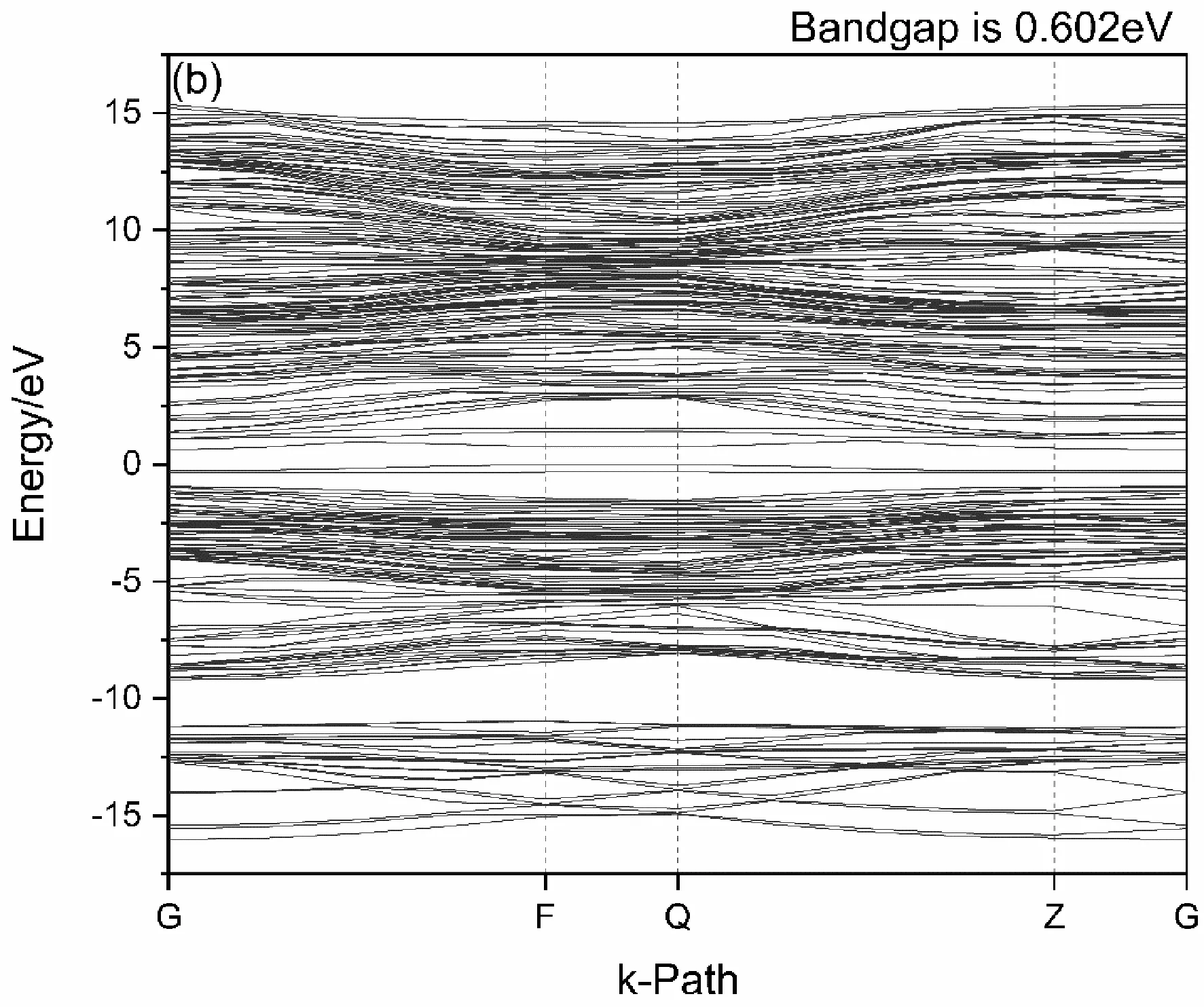
图2 6H-SiC(a)与Mn掺杂的6H-SiC(b)的能带图Fig. 2 Band structures of 6H-SiC(a) and Mn-doped 6H-SiC (b)

3.3 电子态密度分析

为进一步探究Mn掺杂对6H-SiC对电子结构的影响，本文计算了掺杂前后的电子态密度，图3(a)为未掺杂的6H-SiC态密度，总态密度在整个能量区间内分布较为平均，电子的非局域化性质较强. 可以看出，未掺杂体系中，价带部分- 15.7 eV ～ - 9.5 eV处主要由Si - 3s, 3p与C - 2s电子态贡献，价带- 9.9 eV ～ 0 eV处主要由Si - 3p, 3s电子态及C - 2p电子态贡献，形成sp3轨道杂化，并体现在总态密度(TDOS)中. 导带部分1.6 eV ～ 16.7 eV处则主要由Si - 3p，3s电子态及C - 2p电子态贡献，并具有明显sp3杂化特征. C - 2s电子态对能带的贡献较小.

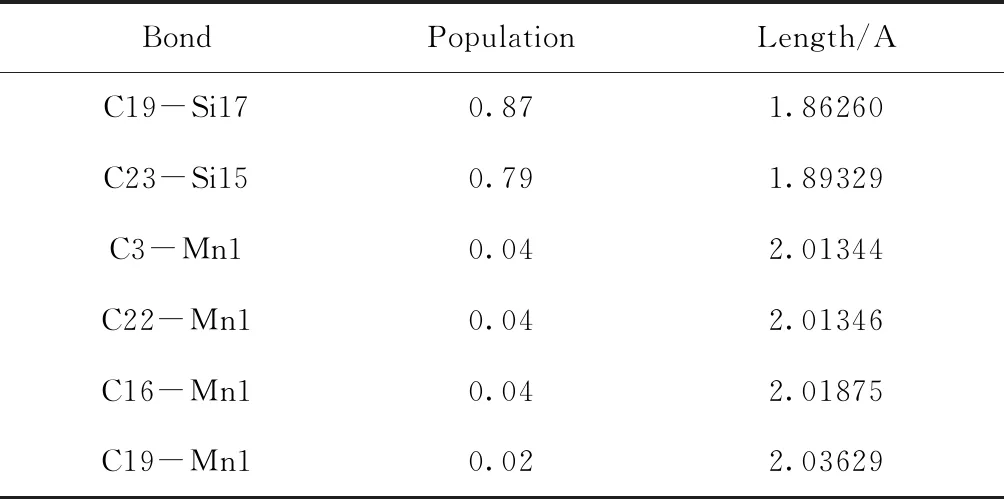
表2 Mn掺杂的6H-SiC的马利肯布居数分析

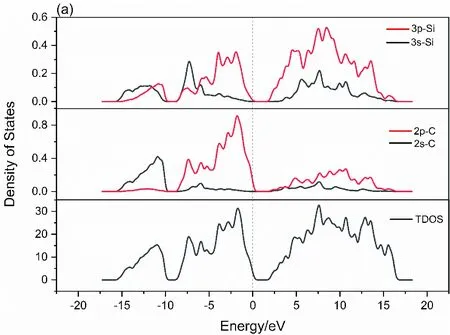
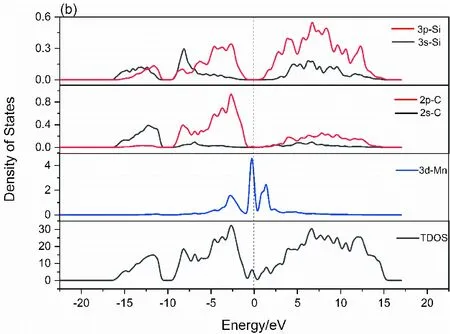
图3 6H-SiC(a)与Mn掺杂的6H-SiC(b)的状态密度Fig. 3 Densities of States of 6H-SiC(a) and Mn-doped 6H-SiC(b)

图3(b)中，在价带部分 - 16.5 eV ～ - 10.4 eV处，主要由Si - 3s, 3p电子态与C - 2s电子态贡献，Mn的各电子态均无贡献. - 9.2 eV ～ - 0.8 eV处Si - 3p，3s电子态及C - 2p电子态贡献，形成sp3轨道杂化，体现在总态密度(TDOS)中. 导带部分0.4 eV ～ 15.5 eV处则主要由Si - 3p，3s电子态及C - 2p电子态贡献，并具有明显sp3杂化特征. TDOS在费米能级附近变化较未掺杂明显，主要由Mn的3d电子态在导带底0.33 eV ～ 2.03 eV处及价带顶 - 0.8 eV ～ 0 eV处作出贡献. 从总态密度(TDOS)可以看出，掺入Mn后对原有的总态密度作用在费米能级处较为明显，价带顶已经穿过费米面形成兼并态，掺入的Mn杂质为受主杂质形成受主能级，在价带顶附近提供大量电子使6H-SiC成为p型半导体. 在引入新的施主杂质Mn后，由于价带顶新生成的杂质能级，形成可以作为电子跃迁的媒介，6H-SiC的带隙由2.022 eV降为0.602 eV，电子从价带跃迁所需要的能量减少，可以让更多的电子与空穴参与到载流子的运输中.

3.4 光学性质

为了研究Mn元素掺杂6H-SiC的光学性质,本文对Mn掺杂前后6H-SiC晶体的介电函数、光吸收谱和反射谱、光电导率进行了计算并分析其影响机制.

3.4.1介电函数

介电函数可以描述系统对电磁辐射的线性响应以及电场对材料的作用，与光子和电子的相互作用有关. 而虚部数值越大，说明电子吸收光子的概率越大，激发态的电子数目就会越多，进而跃迁的概率也就越大[17]. 通过理论计算，得到了介电函数:

ε(ω)=ε1(ω)+iε2(ω)

(1)

式中ε1( ω)为实部 和 ε2( ω)为虚部 ，图4(a)与图4(b)分别为未掺杂的6H-SiC和Mn掺杂后的6H-SiC的介电函数实部与虚部.

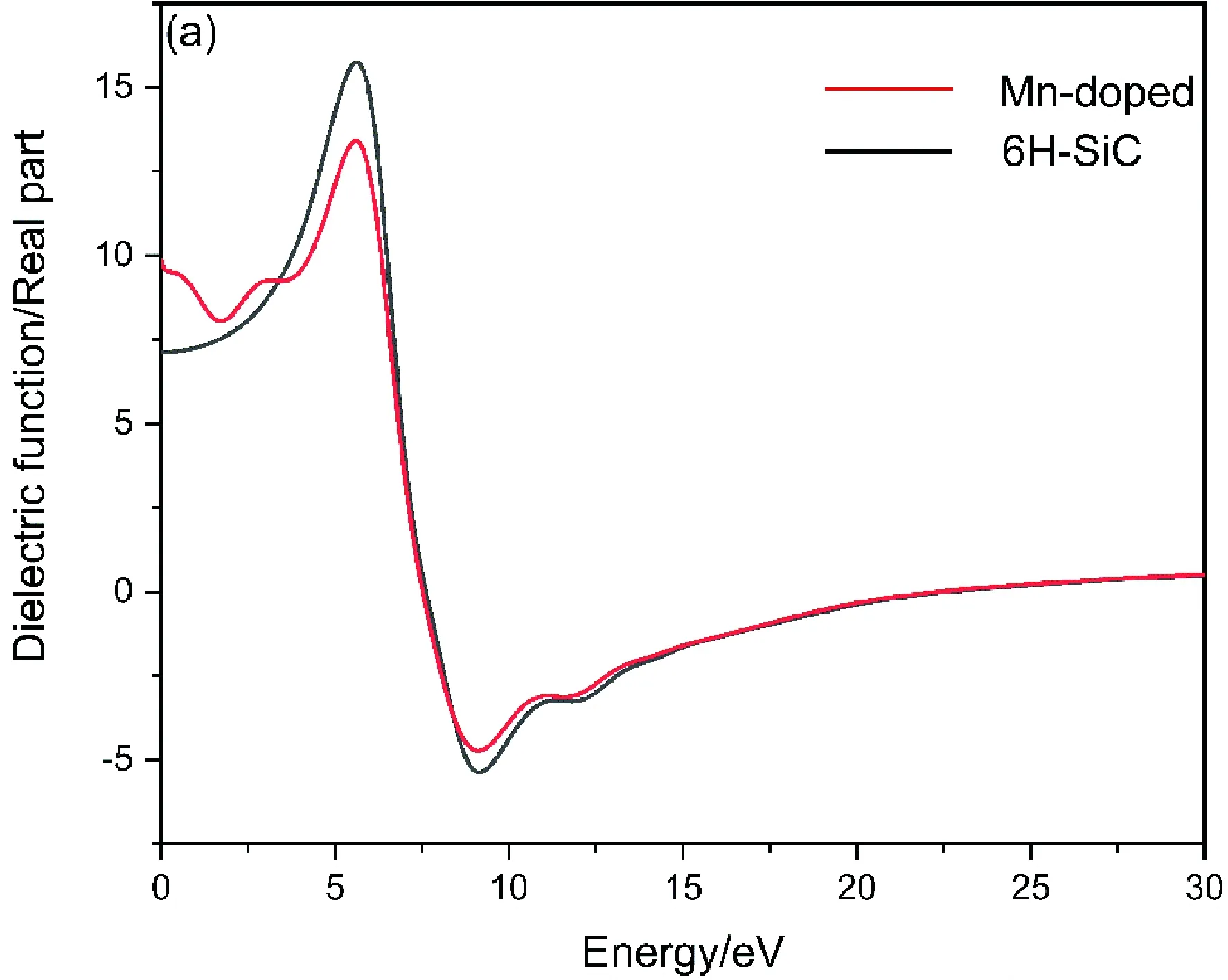
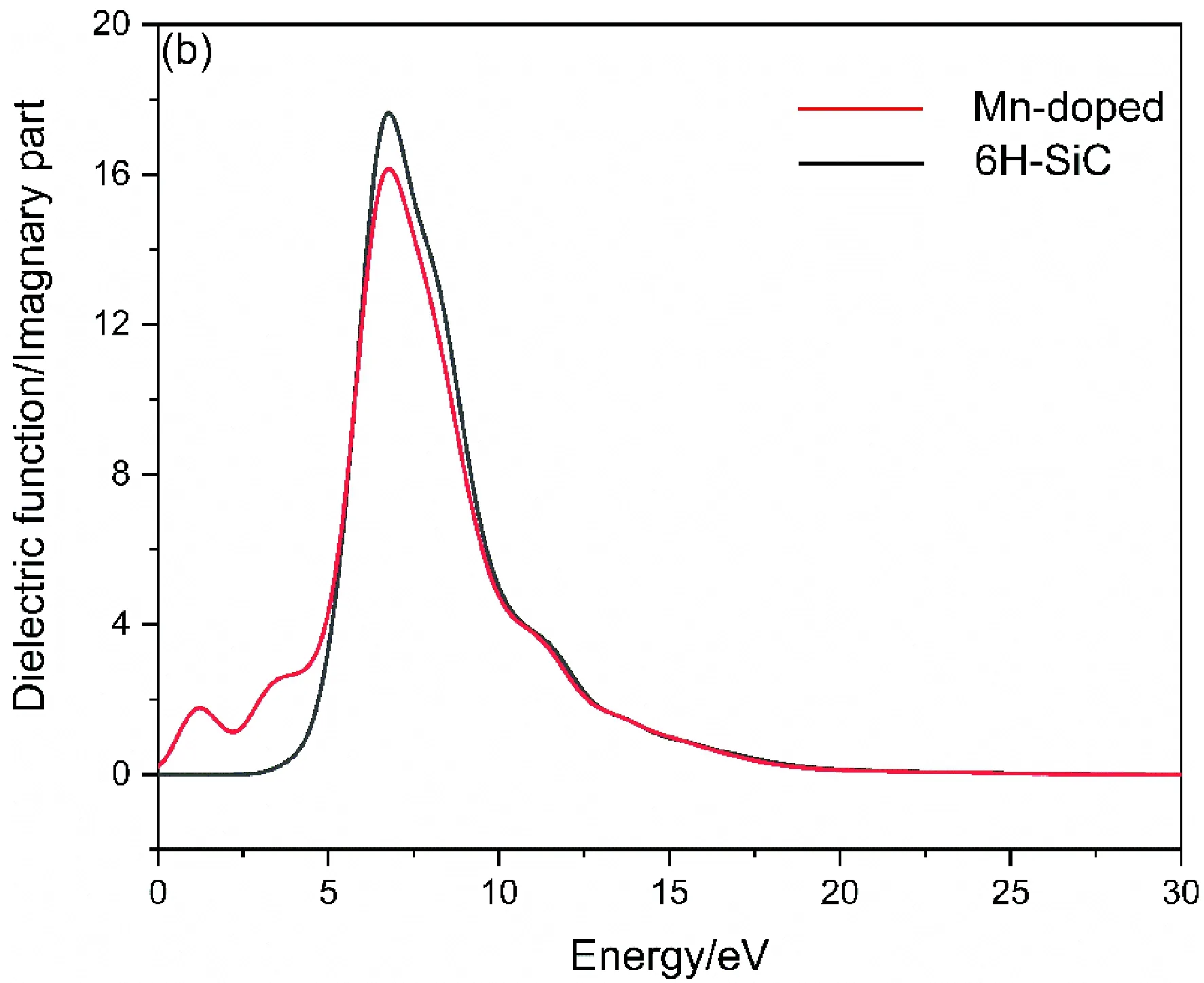
图4 掺杂前后的介电函数实部(a)与虚部(b)Fig. 4 Real part (a) and imaginary part (b) of dielectric function

观察对比两图实部与虚部，主介电峰位置基本一致，由图4(b)可见6H-SiC与Mn掺杂的6H-SiC分别在2.7 eV及0 eV处发生吸收，且在能量大于19.6 eV后不再吸收且不再有大量电子跃迁情况. 在Mn掺杂后，在主介电峰左侧1.22 eV处出现由杂质元素产生的介电峰，分析是由价带电子向所掺杂的Mn-3d轨道跃迁形成，位于6.73 eV处的主峰则是价带载流子向导带运输而产生的.

3.4.2吸收谱与反射谱

图5为掺杂前后的吸收谱对比. 半导体吸收系数指的是光波在此半导体介质中单位传播距离光强度衰减百分比，也可以更直观的展示对太阳能的转换效率[18]. 在图中看到，未掺杂6H-SiC在0 ～ 3.1 eV左右没有吸收. 在8.94 eV处达到吸收最大值，在3.1 eV ～ 31.8 eV处均有吸收. 而在Mn掺杂后，初始能量附近的吸收值较未掺杂6H-SiC发生变化，初始阶段便存在吸收系数，结束端与未掺杂体系类似. Mn掺杂后，吸收系数最大值出现在8.94 eV处，另一峰出现在5.89 eV处.

图5 Mn掺杂的6H-SiC与6H-SiC的吸收谱Fig. 5 Absorption of Mn-doped 6H-SiC and 6H-SiC

图6为掺杂前后反射谱的对比. 在紫外与可见光区域，本征体与掺杂体的反射率曲线大致重合，反射率比较接近. 在0 eV ～ 3.5 eV处反射谱有红移，有潜力作为涂层材料用于隔光隔热.

图6 Mn掺杂的6H-SiC与6H-SiC的反射谱Fig. 6 Reflectivity of Mn-doped 6H-SiC and 6H-SiC

3.4.3光电导率

光电导率显示了随着光照强度的变化，半导体电导率发生的变化. 图7显示了光电导率随光子能量的变化曲线，掺杂前后的6H-SiC基本在同一位置(7.1 eV)处达到峰值. 在能带分析中显示由于Mn原子的掺入使得6H-SiC的能带结构发生变化，带隙掺入Mn后降为0.602 eV，使得光导率的产生范围开始变化，在Mn原子掺入后，由原来的3.03 eV处开始产生的电导率扩展至0 eV，优化了6H-SiC的光学性能.

图7 Mn掺杂的6H-SiC与6H-SiC的电导率Fig. 7 Conductivity of Mn-doped 6H-SiC and 6H-SiC

4 结 论

通过密度泛函理论计算方法对6H-SiC与Mn掺杂的6H-SiC的电子结构与光学性质做了分析. 未掺杂的6H-SiC为间接带隙半导体，计算得其带隙为2.022 eV，掺杂Mn后的6H-SiC为间接带隙p型半导体，带隙为0.602 eV，未掺杂体系中，价带主要由Si的3p电子态及C的2p电子态贡献，导带则主要由Si的3p，3s电子态及C的2p电子态贡献，在掺入杂质后，Mn的3d能级对费米能级处能带结构贡献较大. 光学性质分析中，Mn的掺杂产生新的介电峰，使得介电常数能量范围有所扩大. 吸收谱的分析中看到在Mn掺杂后在0 eV处便有光吸收，光学性质有改善. 反射谱研究显示在可见光和红外波段反射增强. 掺杂以后禁带宽度的降低也使得光电导率开始范围扩展到0 eV. 以上研究为实验提供理论依据.