基于数学形态学的表面原子熔融相的STM图像识别算法

樊甫江， 时国栋， 吴升清， 王中寅， 桂飞林， 商 波， 魏 征

(1. 重庆大学 材料科学与工程学院， 重庆 400044； 2. 重庆大学 机械与运载工程学院， 重庆 400044； 3. 重庆大学 化学与化工学院， 重庆 400044)

1 引 言

结晶和熔化是自然界中极其普遍的物理现象,当晶体温度达到熔点时,便开始熔化,发生有序到无序的结构相变.其相反的过程即为结晶. 液体常常可以保持到低于熔点仍不结晶,即为过冷液体.人们以往的研究对熔化-凝固相变过程的研究大多关注于过冷液体，因为一般实验上很难观测到晶体超过熔点不发生熔化,从而认为过热晶体不存在.一般理论认为，表面在接近但是尚未达到块体的熔点时,会发生连续、可逆的有序-无序转变这一预熔化(premelting)现象.在预熔化状态下，大多数表面原子实际上已偏离了原有点阵的固定位置,形成一层类液层(quasi-liquid layer).类液层的结构、动力学和输运性质介于固体和纯液体之间，为过热晶体的不存在提供了一个合理的解释和依据[1].

对于线型(或轻度网型)非结晶聚合物，绝大多数聚合物材料通常可处于以下三种物理状态(或称力学状态)：玻璃态、高弹态和粘流态.玻璃态和高弹态之间的转变为玻璃化转变，从分子结构上讲，玻璃化转变温度是高聚物无定形部分从冻结状态到解冻状态的一种弛豫现象，玻璃态物质由液体转变为固体不是在一个特定的温度点进行,而是对应一个温度区间(即转变温度范围),在此温度范围内,玻璃由黏性体经黏塑性体、黏弹性体,最终逐渐转变成弹性体[2]. Anderson 在1995年指出玻璃态及其转变是固体物理领域最难也是最有趣的问题之一，需要未来几十年的探索来理解[3].

对于晶体的熔化，前人的实验基本是使用透射电子显微镜开展衍射实验.而原子团的衍射特征，如原子团的2、3、5重对称性[4]，不能准确反映单个原子的实空间位置信息.扫描隧道显微镜(STM)具有高空间分辨的形貌表征能力,可以探测单原子、分子水平上的电子性质和微观过程,如扩散、解吸附、断键等[5]，为研究表层原子熔化过程提供了新的方向.

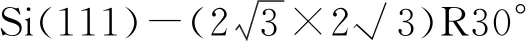
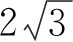
2 数学形态学基本原理

数学形态学是一种应用于图像处理和模式识别领域的图像处理方法，其具有严格完备的数学理论基础，并且和实际又紧密联系在一起.形态学的主要内容是利用一整套概念、运算来描述图像的基本结构特征.腐蚀运算(Erosion operation)与膨胀运算(Dilation operation)是数学形态学的两个最基本变换，其他的变换都是由这两种变换的组合来定义[9,10].腐蚀是使得边界向内部收缩，从而消除物体的所有边界点的过程，膨胀是将与物体接触的所有背景点合并到该物体中的过程，从而使得物体的面积增大相应的点,可以填补空洞和边缘轮廓凹陷部分.采用数学形态学中的腐蚀和膨胀的方法能达到对图像去噪和细化的目的，其主要的技术手段就是用一定形态的结构元素(Structural element)去度量和提取图像中的对应形状[7]. MATLAB中Strel函数主要用来构建形态学的结构元素，语法为strel(shape, parameters), shape表示结构元素形状；parameters为控制形状大小方向的参数.形状参数可以有线形、矩形、盘形、自定义等，本算法中结构元素都采用盘形(disk)，对应parameters为盘形的半径.

2.1 数学形态学开、闭运算

结构元素B对A的开运算(Opening operation)，即采用相同结构元素对A做腐蚀运算，再做膨胀运算记作A°B，定义为：

A°B=(AΘB)⊕B

(1)

其中Θ表示腐蚀运算，⊕表示膨胀运算.开运算具有消除比结构元素小的散点和突刺，切断细长搭接而起到分离作用，即对图像进行平滑的作用，也可以起到低通滤波的作用.但开滤波器只能通过与结构元素形状一致的图像部分[7].

闭运算(Closing operation)是开运算的对偶运算，采用相同结构元素对A做膨胀运算，再做腐蚀运算.结构元素B对A的开运算，记作A·B，定义为：

A·B=(A⊕B)ΘB

(2)

闭运算可以把比结构元素小的缺口或孔洞填充上，搭接小的间断从而连接邻近物体[7，9].

2.2 高、低帽滤波

从一幅原始图像中减去对其做开运算后得到的图像，可以得到一些重要的标记.该方法对在较亮的背景中求较暗的像素聚集体(颗粒)，或在较暗的背景中求亮的像素聚集体非常有效.灰值形态学中的高帽(Top-Hat)与低帽 (Bottom-Hat)变换分别能满足上述两方面的要求，因此可用于检测图像信号中比结构元素小的灰度峰值和谷值[9].

Top-Hat变换的定义为:

Top-Hat=A-(A°B)

(3)

通过高帽滤波可以增强图像的对比度，使得图像更加清晰.

Bottom-Hat变换的定义为:

Bottom-Hat=A-(A·B)

(4)

通过低帽滤波可以获取图像的边缘.

3 算法实现

3.1 处理流程

实验得到的图像将其按加热温度顺序制成视频，算法先将视频分割成各帧图像，再针对每一帧进行图像处理.STM图像必须为灰度图.首先进行高低帽滤波与去噪，调整灰度值从而提高对比度.再二值化(Binarization)生成二值图像.由于在熔融相也有较亮的小点而导致统计误差特别大，要进行形态学的开运算将其去除.由于在未熔化原子之间区域的灰度值和熔融区域灰度值接近，不能将这一部分判定为熔化原子，不能简单处理为背景与目标的关系，需要将一整块未熔相区域进行面积统计.膨胀运算将未熔化原子个体范围扩大，闭运算将小的间隙消除掉，使得整块未熔相区域连通起来，从而便于进行面积统计.最后采用像素统计方法进行数目统计.实验时存在原子排列缺陷，这一部分既不属于熔融相，也不属于未熔相，需要剔除掉.最后得到一张图像中，未熔相区域所占的比例.

未熔相区域所占的比例

(5)

算法运行流程如图1所示，其中有三条主要流程，分别为一般处理流程，即黑色实线；对于缺陷部分的处理，即蓝色虚线，对于大部分原子熔化图像的处理，即红色实线.具体将在下面进行说明.

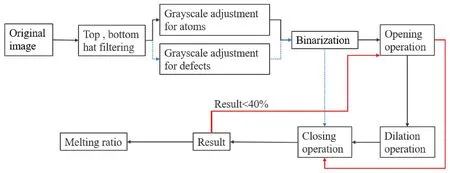
图1 处理流程图Fig. 1 Flow-chart of the procedure.

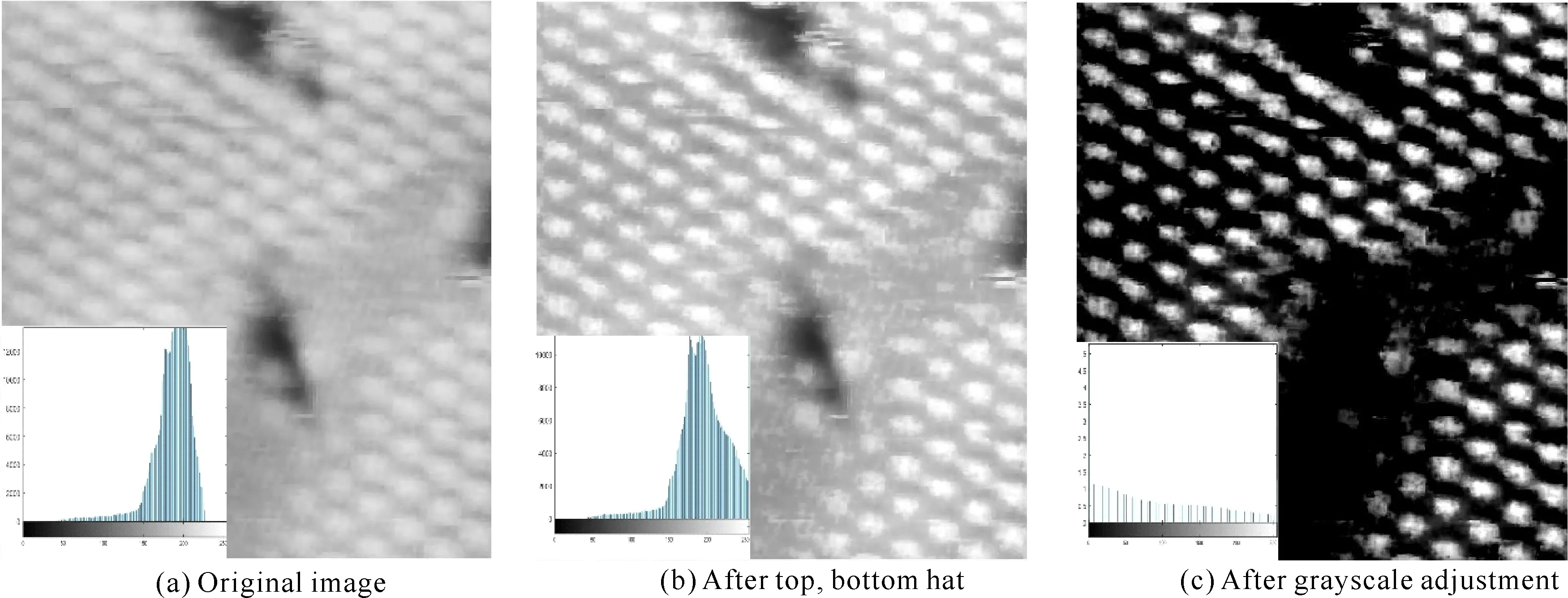
图2 (a-c)原图、分别经过高低帽滤波和灰度调整处理后的图像及其相应的直方图Fig. 2 (a) Original image, (b) image after top-bottom hat filtering and (c) image after grayscale adjustment, with the histograms as insets .

3.2 高低帽滤波和灰度值调整

实验得到的灰度图(图2(a))比较模糊，从其灰度分布直方图(图2(a)左下角)可以看出，灰度范围较集中，为便于进行阈值分割，突出原子的外形轮廓，提高其对比度是十分有必要的.通过高帽滤波，可求出图像灰度的峰值，而低帽滤波可以求出灰度的谷值，经过高低帽滤波，然后在原图上加上高帽滤波结果再减去低帽滤波的结果，可以提高对比度.在MATLAB中，选择结构元素Se1为disk，圆盘的半径值的设置需要恰当，过小则对比度提高较少，过高将使得非原子区域亮度过高，带来误差.

从滤波后的灰度分布直方图图2(b)左下角可以看出，高灰度值有很大的增加，而分布仍然较为集中与狭窄，动态范围小，为突出轮廓、便于后续二值化的进行，将滤波后的图像进行灰度值调整. 根据灰度分布直方图，灰度分布集中于170至220之间，取其平均值为195.将灰度值小于0.75×255的灰度值设置为0，大于1×255的灰度值设置为255，大大提高对比度.由灰度调整后的灰度分布直方图图2(c)左下角可以看出，灰度值主要为0和255，而中间的灰度分布均匀且较少.

3.3 阈值分割

将图像二值化的目的是分割其目标物体(未熔化原子)和背景，关键在于判断像素点是属于背景还是目标，判断的方法是确定一个灰度阈值，大于其则属于目标区域，小于则为背景区域.为实现阈值的自动确定，算法采用最大类间方差法(OTSU法)，OTSU算法是由日本学者OTSU于1979年提出的一种对图像进行二值化的高效算法[11]，该算法是在灰度直方图基础上采用最小二乘法原理推导出来的，使得分割的两部分灰度值之间的方差最大，具有在统计意义上的最佳分割阈值，且速度快，但对噪声较敏感.

分割效果如图3(a)所示，大部分原子熔化时，存在许多的小亮点，这些是图像生成时灰度值较高的点，但不属于未熔相，统计时这些亮点被计入将造成很大误差，必须消除.

3.4 形态学处理

3.4.1开运算

为解决上述问题，需要进行形态学的开运算. 此处结构元素Se2的圆盘半径值设置也需要适当，过大将使得在未熔相区域中，亮度高的原子由于尺寸太小而被消除掉，使得统计值偏小；过小将使得噪点去除不彻底，统计值偏大.结果如图3(b)所示.

3.4.2膨胀运算

由于要统计的面积为整个未熔相区域，不能直接统计原子个数，需要将未熔原子连接起来.形态学的膨胀操作，使得原子的范围增大，从而互相连接在一起.当然，膨胀的结构元素Se3圆盘半径值设置得也要恰当，过大使得原本属于熔融相的区域也被算入未熔相区域，过小则达不到连通的目的.运算结果如图3(c)所示，图中未熔相和熔融相区域分割得效果较好，而在大部分原子熔化图像中，未熔化原子的边界膨胀得过大，使得统计值偏大，要另外处理.

3.4.2闭运算

由图3(c)见，在未熔相区域也存在没有完全连通的缺口，这是这个位置灰度较低，膨胀后无法完成连通.通过闭运算可以将外部轮廓不够光滑的原子轮廓光滑化，填充原子之间的小间隙.处理结果如图3(d)所示，效果很好，但仍有部分地方没有完美解决，如图像边界，这是由于结构元素Se4圆盘半径值是根据整个熔化过程视频来整体取的，需要考虑到尽量使得每张图片统计结果误差最小.如若结构元素Se4取半径值过大，导致熔融相区域算入未熔相区域，使得结果偏大，设置过小将导致连通效果不好，边缘未统计到的区域偏多，结果偏小.

3.5 大部分原子熔化图像的处理

对于大部分原子熔化的图像，膨胀过度使得熔融相区域算入未熔相区域，为了更准确的得到这些标定缺陷的参照原子面积，在经过开运算去除较小的亮点后，不进行膨胀处理，而是结构元素Se5取大一点的半径值直接进行开运算，进一步处理掉较小的亮点，如图1红色实线所示.

3.6 缺陷区域的处理

缺陷是由于原子排列不满而形成的，可以作为熔化时原子热漂移的参照，这一部分既不属于熔融相，也不属于未熔相，在统计时应剔除掉.采用如上相同的方法，经过灰度调整，将0.6×255以下的灰度进行调整，提高对比度，二值化后直接统计黑色部分的面积即为缺陷的面积，如图1蓝色虚线所示.

图3 分别经过(a)阈值分割后、(b)开运算、(c)膨胀运算和(d)闭运算处理后图像Fig. 3 Images processed after (a) threshold segmentation,(b) opening operation,(c) dilation operation, and (d) closing operation.

4 结果与讨论

算法的实际使用是在对于原子熔化过程视频的处理，这里选择三帧代表性的图像进行展示.如图4中(a)为小部分区域的原子熔化，(b)为近一半区域的原子熔化，(c)为大部分区域的原子熔化的图像．其中绿色线条包围的区域为缺陷区域，红色线条包围的区域为原子区域.

人工计数采用方格法，即现在一帧图片上用方格划分熔融相区域，再统计区域的面积. 人工计数方法划分的各相的边界不连续，为锯齿状,存在过度统计和过少统计的情况，且基于视觉判断，存在很大人主观选择带来的误差，而算法统计基于图像实际灰度高低反应原子的高度，且边界光滑连续，更精确且无人的主观影响.

图4 统计的区域和缺陷区域Fig. 4 Regions to be counted and defect parts

处理消耗时间方面，手工处理一帧约需要3分钟，243帧需要43740秒，而程序运行处理一个243帧的movie所用时间为164秒，约为手工的1/266，程序的使用大大提高了统计效率，减少了人的主观误差.

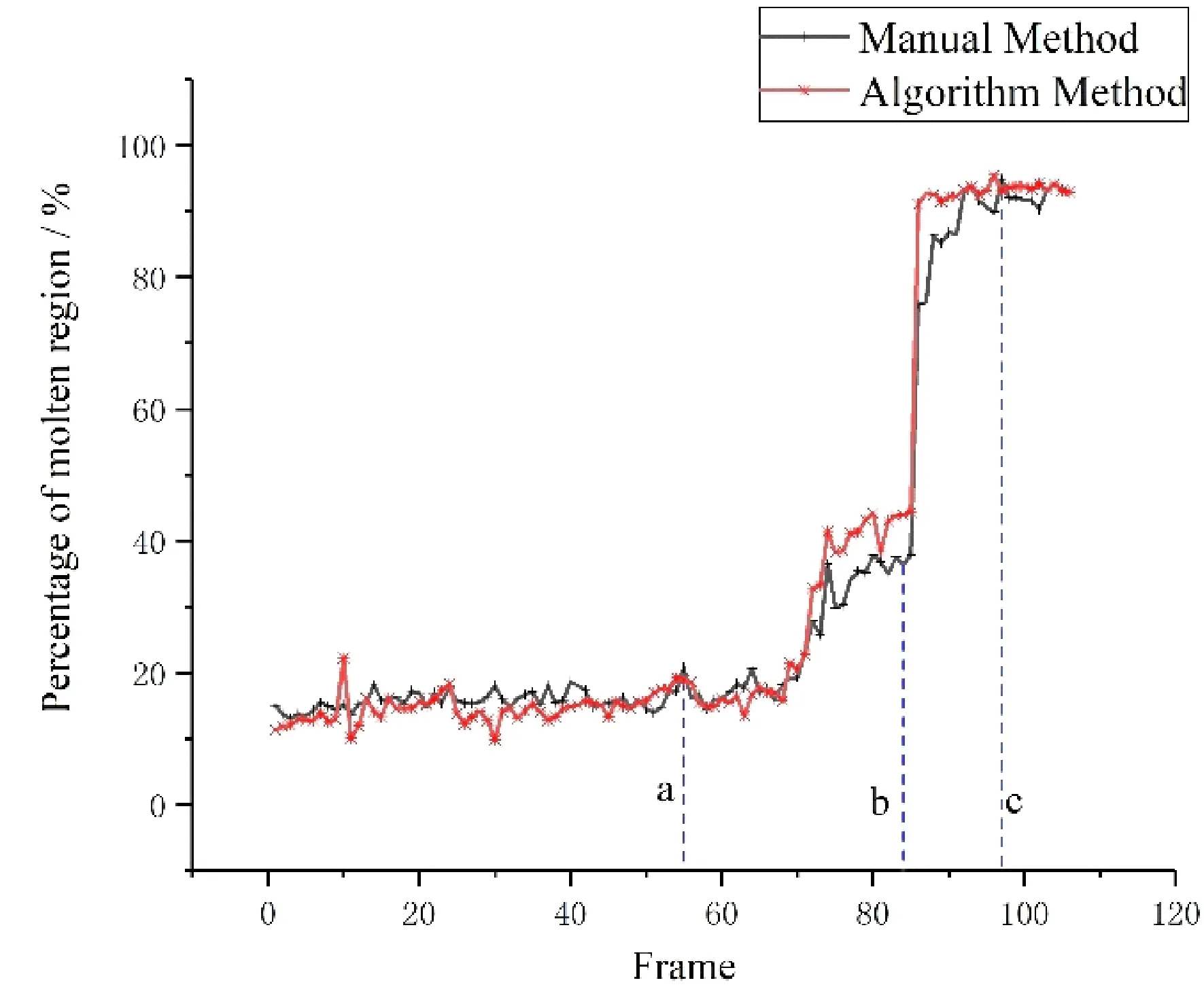
图5 算法和人工计数结果对比Fig. 5 Results derived from algorithm vs. manual method.

熔化过程未熔相占比曲线如图5所示，对比人工计数的曲线，整体上，算法计数有较好的拟合效果，但细节上存在许多误差波动.图4中图(a)，(b)，(c)对应于图5上的 a，b，c三个数据点.可以看到a帧算法结果与人工方法结果匹配度很高，而b和c帧附近，算法结果都较人工方式偏大.通过实际划分边界的对比，算法确定的边界比人工的更准确，人工统计熔融相偏小，从而导致比值偏小.

5 总 结

本文以数字形态学处理方法为基本原理，编写了一套处理和统计表层原子熔化过程STM图像中未熔相所占比例.通过更改基本的结构参数值进行实验，经过大量的对比、参数优化，选择了对于视频整体最为合适的参数，既保证统计的内容噪音尽量少，又保证不把基本的未熔化原子信息给忽略，再进行统计计数.算法的使用，大大缩短处理与统计的时间，消除人的主观影响带来的误差，实现高精度、高效率.对于单张图像的处理，可以通过人机交互，更改输入的参数，实现合理的区域取舍，从而使得该张图片的处理精度达到最佳.