最优阶次多项式响应面法及其在模型修正中的应用

王涵，史治宇

(南京航空航天大学 机械结构力学及控制国家重点实验室，江苏 南京 210016)

0 引言

有限元方法是一种运用离散思想对连续性问题进行近似求解的数值方法，在工程领域中应用广泛[1]。实际工程问题中由于边界条件、连接等简化建模，模拟参数常常存在误差，有限元模型往往不能准确反映真实模型情况。因此有限元模型(finite element model,FEM)修正技术应运而生，旨在通过试验数据修正有限元模型，从而获得更符合真实情况的有限元模型。经典参数型模型修正理论中的迭代计算需反复调用有限元软件，尤以灵敏度矩阵的计算耗费大量时间[2]，因此在处理实际工程问题时存在计算效率低的问题。为了减少计算耗时同时保证计算精度，响应面法(response surface method,RSM)开始应用于模型修正领域。响应面法是统计学中的综合试验技术，通过拟合初始模型中输入与输出之间的隐式关系，获得具有显式函数关系的响应面模型[3]。采用响应面法将初始模型简化为代理模型进行的修正计算，避免了灵敏度矩阵模块的调用，简化了输入、输出间的软件计算，对动力学分析和优化具有重要意义。

响应面发展出多种近似方法，例如多项式法、神经网络法、径向基法等。针对不同问题背景选取合适的响应面建立方法，有益于提高代理模型精度。相较于其他响应面近似方法，多项式法因其计算更简便、可处理大多数非线性问题的优势而得到了广泛应用[4]。常规的多项式响应面法通常采用二阶完全多项式进行构建，阶次和变量形式固定，存在精度较低、无法准确反映高阶模型的缺点[2]。面对非线性程度较高的输入、输出，可以通过适当提升多项式阶次来达到更精确的拟合。然而随着阶次增高，参数组成的变量将呈指数爆炸增长；各交叉项[5]的显著度存在差异，取舍不当会影响拟合效果；最高阶次选择不当，易产生过拟合的问题，且传统多项式中所有参数拟合阶次相同，忽略了不同参数对输出映射之间的差异。因此盲目采用高阶完全多项式，可能出现计算时间增长、模型精度下降等情况，违背了使用代理模型的初衷。同时，代理模型的精度较低时，会引发模型修正误差的增大，因此建立高精度的响应面模型是其应用于模型修正的前提。综上，可以探寻一种区分不同参数对输出的最优阶次，使得参数间的拟合阶次不再固定的多项式响应面构造方法，并将其应用于模型修正领域。

本文在此提出一种最优阶次多项式响应面的构造方法，在传统2阶多项式基础上提升并区分了参数对响应的拟合阶次，以突破阶次固定统一的限制，提升代理模型的精度。同时将改进的响应面法应用于模型修正领域，以解决经典修正过程中耗时长的问题，并保证修正结果的精度。本文首先阐述了最优阶次响应面的构造方法，包括最优阶次判定、多项式构造以及精度检验，接着建立了运用最优阶次响应面进行模型修正的基本理论。以功能函数为例，采用改进后的响应面有效实现了函数模型的还原；以GARTEUR飞机模型为例,以真实试验数据为目标值,利用基于最优阶次多项式响应面法的有限元模型修正方法对弹簧单元刚度等3个设计参数进行了有效修正。

1 基本理论

获得高精度响应面模型的基础是试验设计，即选择合适的结构模型参数试验样本点，使响应面拟合函数在整个参数空间内能最有效地描述参数和响应之间的隐式关系。试验设计方法包括析因实验设计、中心复合设计 (CCD)以及Box-Behnken设计等。建立参数与响应间的显式关系即对样本进行拟合。常规的多项式拟合一般采用2阶完全多项式，表达式如下:

(1)

其中α0、αi、αii、αij为多项式系数。为了更适应于样本特性，提升拟合效果，可以通过判断单个参数对响应的最优拟合阶次，构造一种区分参数拟合阶次的多项式响应面，具体理论如下。

1.1 最优阶次判定

最优阶次是指样本数据中单参数对响应的最佳拟合阶次。设有m个参数与n个响应，共判断m×n个最优阶次。单参数x对单响应y的最优阶次，通过逐阶增添回归变量中幂次项的多元回归对比分析。

设阶次判定上限为k，从第2阶起，幂次项每增加1阶，建立共k-1个回归方程。各阶回归方程见式(2)。

(2)

其中a0、a1、ai为系数。共得到k-1个回归函数，即单变量对单响应的2-k阶回归函数组。

最佳拟合函数的选择采用拟合优度与显著F检验结合的方法。拟合优度指回归函数对观测值的拟合程度，由可决系数R2来度量。R2的值越接近1，回归函数对样本值的拟合程度越好。显著性F检验则为判定回归假设为0的概率，并用p值来量化。p值越小，则越拒绝，即回归越可靠。为保证整体回归的精度和回归系数的显著，将两种指标结合，取判定指标δ：

δ=R2-p

(3)

其中：R2为可决系数；p为显著性概率，可通过拟合工具软件计算。对每阶回归函数进行相应δ值计算，可建立k-1维数组D：

D=[δ1;δ2;δ3;…;δk-1]

(4)

D最大值对应的拟合函数回归精度最高，回归系数最显著，其幂次项最高阶次即为单参数对单响应的最优拟合阶次τ：

δi=Dmax

(5)

τ=i+1 (τ≥2)

(6)

通过对每个参数和响应进行阶次τ判断，组成最优阶次矩阵Ord：

(7)

Ord针对不同参数对不同响应的阶次做到了逐个区分，但由于试验设计获取的样本数据通常没有进行单变量控制，最优阶次的判定并不能反映参数与响应之间的物理特性关系。

1.2 多项式响应面构造

由于不同参数之间阶次存在差异，高阶交叉项的组合也变得十分复杂，固定形式的多项式不再适用。为了保证多项式构造方法的简便性，在式(1)的基础上，增添所有参数的2阶及2阶以上幂次项，形式如下：

(8)

其中：α0、αi、αij为多项式系数；βiε为参数i的第ε幂次项系数。若Ord各项均为2，则最优阶次多项式即为2阶完全多项式。

根据式(7)-式(8)，共构造n个响应的多项式函数，代入样本点计算得相应系数值后，该组函数表达式即为最优阶次多项式响应面模型Y：

Y=[y1;y2;y3;…;yn]

(9)

最优阶次多项式实现了参数间阶次的提升与区分，避免了高阶交叉项的复杂组合，突破了固定的阶次和变量形式，在提高精度的同时控制了计算量。初步建立响应面模型后需进行精度检验。

1.3 精度检验

响应面模型可以从两方面检验精度，一是统计意义上，可将拟合优度可决系数R2或均方误差MSE作为检验标准。R2值越接近1，得到的响应面模型越接近有限元模型；MSE则正好相反：

(10)

(11)

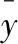
二是从力学角度进一步验证，这部分可以结合其在有限元模型修正中的应用来进行。

最优阶次多项式响应面在构建过程中非常依赖样本数据，不同数据可能得到不同阶次判定结果。当精度检验结果不够理想时，应返回重新进行试验设计。

1.4 模型修正中的应用

应用响应面法进行模型修正时，模型修正可看作优化问题：

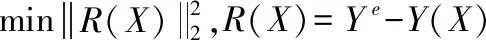
(12)

其中：X为待修正参数；Ye为试验值；Y(X)为响应面计算值；VLB和VUB为X的设计范围。求解如下：

R=SΔX

(13)

其中：R为响应残差；S为灵敏度；ΔX为参数残差。有限元软件中灵敏度采用Nelson法计算[6]，而响应面模型建立后可跳过有限元软件的调用，利用拟合函数的偏导计算灵敏度，求解如下：

(14)

修正后若误差收敛，则修正完成，否则需重新进行试验设计构造响应面。将修正后参数值代入初始有限元模型中，获得修正后的有限元模型。最优阶次多项式响应面法应用于有限元模型修正的流程总结如图1所示。

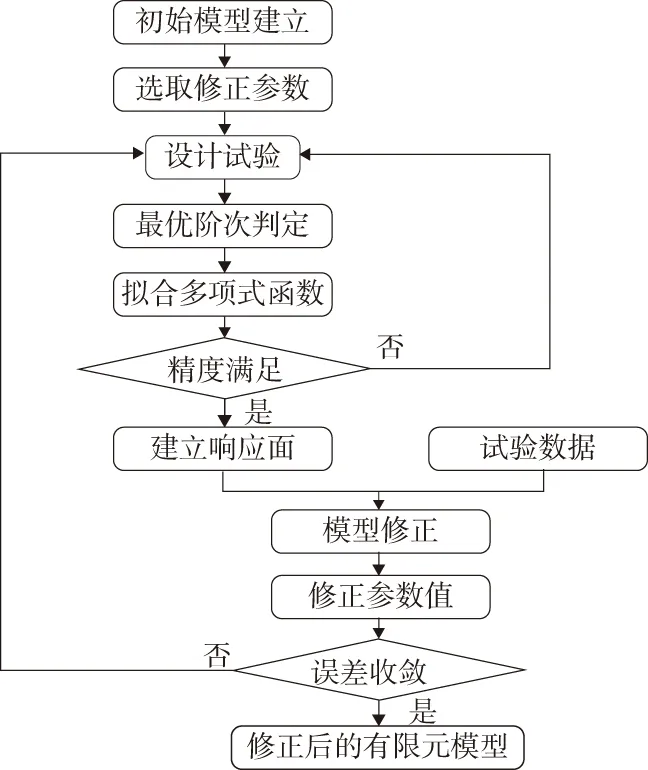
图1 最优阶次多项式响应面法应用于有限元模型修正流程图

2 算例

2.1 功能函数

功能函数[7]定义如下:

其中：X1∈(0,1)；X2∈(0,1)。

功能函数响应面如图2所示。

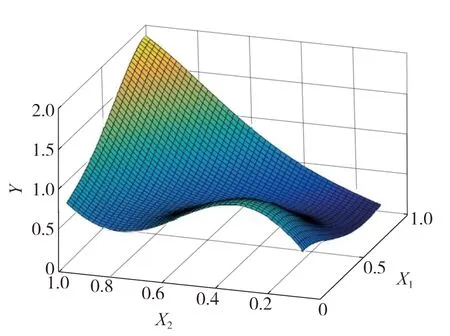
图2 功能函数响应面

通过拉丁超试验设计，获取20组样本点，以此进行改进前后两种响应面的拟合。经过式(1)计算，建立2阶完全多项式响应面，如图3所示。

图3 2阶完全多项式回归响应面

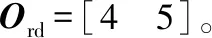
矩阵中显示，参数1对响应的阶次提高到4，参数2对响应的阶次提高到5。接下来根据式(8)-式(9)建立最优阶次多项式响应面Y，如图4所示。

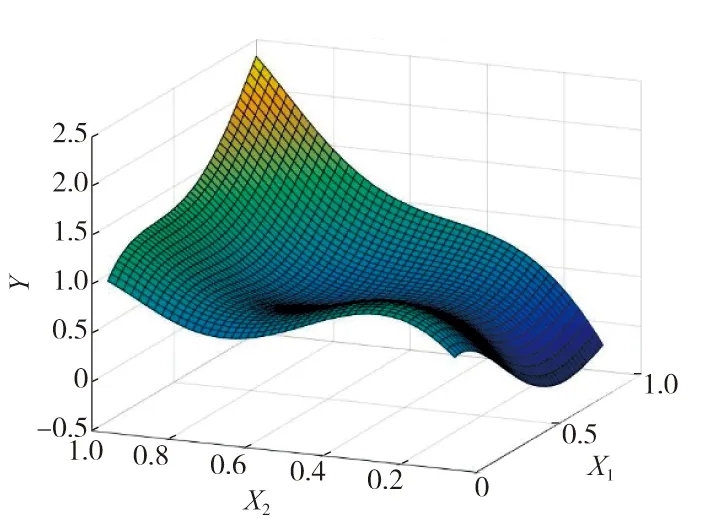
图4 最优阶次多项式回归响应面

两种响应面初步建立后，可以从图像上直观看出，最优阶次多项式更好地还原了功能函数的趋势分布，但在边界角点处仍存在可见差异。分析认为是由于拉丁超试验设计方法中遵循分层概率区间取样，样本点落在角点边界附近较少，影响了边界处的拟合精度。

以R2和MSE为统计指标对两种响应面的精度进行检验，相关计算见式(10)-式(11)。数据对比见表1。

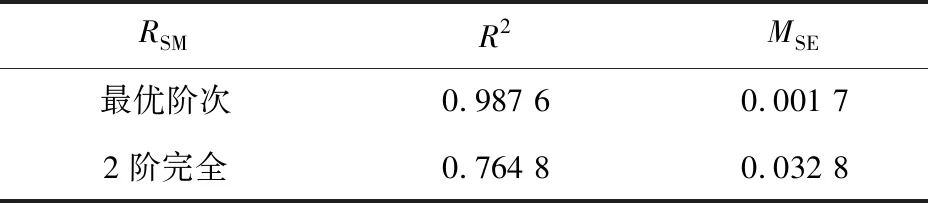
表1 两种多项式响应面模型精度对比

表1数据显示，最优阶次多项式响应面的拟合优度非常逼近于1，相较于2阶完全多项式提升了29.1%，且MSE更加趋近于0。表明该改进的响应面具有更高的精度，更真实地还原了功能函数。由于样本点处均达到了良好拟合，所以角点的误差并未影响整体精度。

2.2 GARTEUR飞机

GARTEUR飞机模型为法国国家航天研究院(ONEDR)设计制造,被定为评估有限元模型修正技术的基础模型。该飞机具有机身、机翼、平尾和垂尾4个主体部分，材料主体为铝，翼展长2 m、机身长1.5 m，总质量38.3 kg。GARTEUR 模型照片如图5所示，建立GARTEUR初始有限元模型如图6所示。

图5 GARTEUR模型

图6 GARTEUR有限元模型

初始有限元模型共46个二维梁单元，包含4种梁属性，分别为机身的梁单元、机翼的梁单元、平尾的梁单元以及垂尾的梁单元。另有8个弹簧元，包含5种弹簧元属性，如图6所示，包括在机翼与机身连接处1，用于模拟左、右机翼对机身绕x轴方向抗弯强度的弹簧单元；在垂尾与机身的连接处2，分别用于模拟垂尾绕x轴和绕z轴方向抗弯强度的两种弹簧单元；在平尾与垂尾的连接处3，分别用于模拟垂尾绕x轴和绕y轴方向抗弯强度的两种弹簧单元。有限元模型共52个节点，312个自由度。对GARTEUR模型进行有限元分析，其前5阶固有频率见表2。

表2 初始有限元模型前5阶固有频率 单位：Hz

其中第1阶主要为机翼绕x向的一弯，第2阶主要为垂尾绕x向一弯，第3阶主要为垂尾绕y向的一弯，第4阶主要为机翼绕x向的反对称二弯和平尾绕z向转动的组合，第5阶主要为平尾绕z向的转动。

根据实测试验结果，模型的实测前5阶固有频率与有限元计算值存在误差，目标值与初始值的相关数据对比见表3。

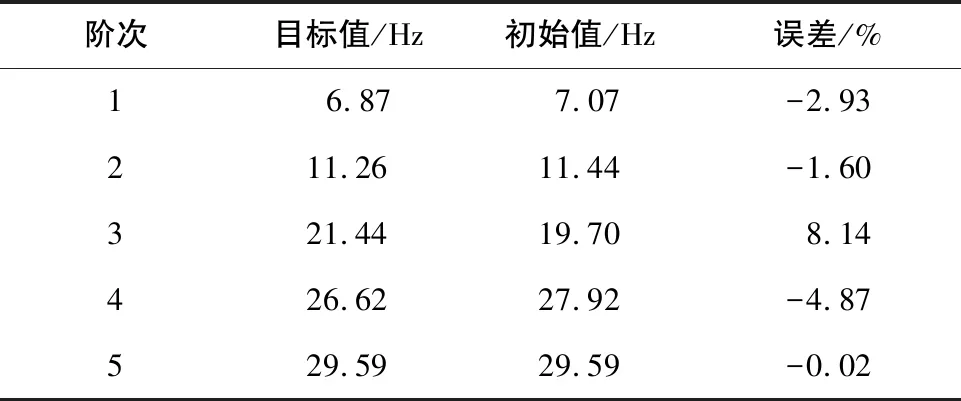
表3 前5阶固有频率目标值与初始值对比

为修正频率误差，应选取合适参数对有限元模型进行修正。考虑到连接刚度不易准确建模，在此选取机翼与机身连接处绕x向转动的连接刚度pelas11、平尾和垂尾连接处绕y向转动的连接刚度pelas15、与垂尾与机身连接处绕x向转动的连接刚度pelas16三个弹簧单元刚度作为三个待修正参数，位置如图6所示，初始建模数据如表4所示。

表4 弹簧单元刚度初始建模值

依据图1流程，对GARTEUR模型进行基于最优阶次多项式响应面法的模型修正。下文中将把3种弹簧单元简称为3个参数，5阶固有频率简称为5个响应。

设定3个参数合理的设计范围，分别为：[1.8,4.2]、[1.56,3.64]、[1.02,2.38]。以5阶固有频率为响应，进行中心复合试验设计，获得15组样本数据。结合工程实际情况，设定阶次判定上限k为5。经过式(2)-式(7)计算，获得最优阶次矩阵Ord：

结果显示，参数1对响应2、响应3的阶次提高到4，参数2对响应4的阶次提高到3，参数3对响应1、响应4、响应5的阶次分别提高到4、4、3。接下来根据式(8)-式(9)建立最优阶次多项式响应面Y。

在此选取第4阶固有频率作为典型响应进行回归响应面绘制，见图7、图8。响应面模型计算第4阶固有频率范围为[25，29] Hz，真实试验数据中第4阶固有频率为26.62 Hz，说明参数上下限取值范围合理。

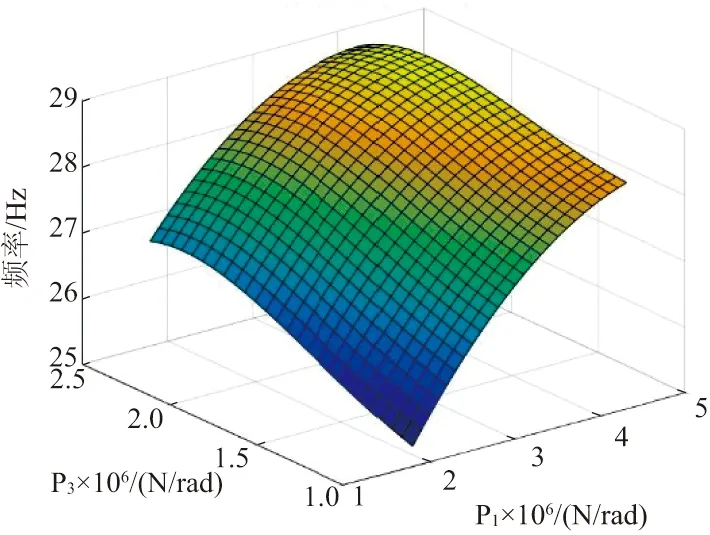
图7 第4阶固有频率对参数1、参数3回归响应面

图8 第4阶固有频率对参数2、参数3回归响应面

根据式(14)，对初步建立响应面模型进行参数灵敏度计算，结果如图9所示。

图9 响应面模型灵敏度计算结果

响应面初步建立后，以R2为指标对最优阶次多项式响应面的精度进行检验，相关计算见式(10)。同时以同组样本数据建立2阶完全多项式响应面，将其精度作为对照，数据对比如表5。

表5 两种多项式响应面模型精度对比

表5数据显示，最优阶次多项式响应面的5个响应拟合优度都非常逼近于1，表明该响应面完成了良好的数据拟合，且在部分阶次中最优阶次多项式模型较2阶完全多项式拟合优度略有提升，表明该响应面模型具有更高的精度。由于该算例模型简单，参数较少，运用2阶完全多项式拟合也可达到较高精度，且两种响应面间参数阶次差异较小，因此精度提升空间并不高。

接下来利用真实试验数据对最优阶次多项式响应面模型进行修正。相关数据代入式(12)-式(14)，经过4次迭代计算后误差收敛，获得修正后结果。修正前后参数值对比见表6，修正前后响应值对比见表7。

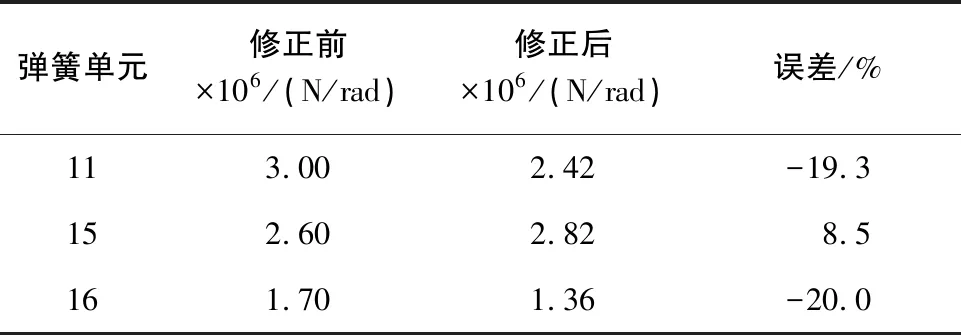
表6 修正前后参数值对比

表7 修正前后响应值对比

表6数据显示，参数修正后变化幅度在20%以内，没有超出参数设计变化范围。表7数据显示，频率的平均误差从修正前的3.52%下降到修正后的1.79%，说明最优多项式响应面模型可以在模型修正中进行有效的模型替代和良好的优化计算。其中响应1和响应5的误差略有放大，分析是由于部分参数灵敏度趋近0，可能引起矩阵奇异、误差不收敛的情况。

为进一步检验最优阶次多项式响应面在模型修正中的结果精度，在此进行3种修正情况的对比：不使用响应面的经典模型修正，使用2阶完全多项式响应面的模型修正以及使用最优阶次多项式响应面的模型修正。达到误差收敛时3种修正方法分别迭代了8次、2次和4次。相关数据对比见表8。

表8 3种修正情况的结果误差对比 单位：%

表8数据显示，初始有限元模型修正前的平均误差为3.52%，不使用响应面修正的平均误差为2.81%，使用2阶完全多项式响应面模型修正的平均误差为3.30%，而使用最优阶次多项式响应面模型修正的误差达到1.79%，表明3种修正方法都可以有效修正初始模型频率的误差。3种修正方法中都存在少数响应误差放大的情况，因为部分参数灵敏度接近于0，会产生矩阵奇异误差不收敛的情况。对比可得：1)修正中使用响应面与不使用响应面相比，无需调用有限元软件，且迭代次数下降。但2阶多项式响应面修正结果误差较不使用响应面的修正结果有所提高，分析认为是代理模型的精度不够而引发了误差。2)使用最优阶次多项式响应面与完全2阶多项式响应面相比，迭代次数少量增加，但修正结果更接近真实数据，并且少数响应误差放大情况得到了改善，计算效率和修正结果精度更高。

3 结语

本文提出了一种最优阶次多项式响应面法的构建方法，解决了常规多项式响应面法阶数限制的问题，区分了多项式中不同参数间的阶次特性，提高了响应面模型的精度。将改进的响应面法应用于模型修正中，降低了经典修正过程中反复调用有限元软件灵敏度模块消耗的计算量，减少了由于代理模型精度不够引发的修正结果误差。数值算例表明该改进响应面法可以提高传统响应面的精度；GARTEUR算例表明该响应面法可以成功应用于模型修正领域，并通过提高代理模型的精度而有效减少修正误差，提高修正效率，具有良好的应用前景。