同轴面齿轮传动系统动态均载特性研究
2021-12-27单来阳李政民卿张红
单来阳,李政民卿,张红
(南京航空航天大学 直升机传动技术国家级重点实验室,江苏 南京 210016)
0 引言
同轴面齿轮传动系统是一种新型的齿轮分汇流传动系统,与传统的面齿轮分流-圆柱齿轮并车传动系统[1]相比,其结构紧凑、零部件数目更少;相比于圆柱齿轮分流-并车传动系统[2],多出了换向功能,减少了系统的传动级数,实现减质量。因而在直升机传动系统中具有重要的应用价值。
国内外学者针对同轴面齿轮传动系统的均载问题进行了研究。FILLER R R和HEATH G F等[3-4]搭建了同轴面齿轮传动系统静力学均载试验平台,通过输入齿轮与上、下面齿轮缓慢啮合来测量输入转矩在上、下面齿轮间的分配量。LI S等[5]研究了同轴面齿轮传动布置对静力学均载的影响。赵宁等[6-7]建立了系统静力学及动力学均载计算模型,研究了系统刚度、误差等参数对系统均载的影响。
目前,针对同轴面齿轮传动系统均载研究主要集中在静态均载上,对动态均载的研究相对较少。本文建立了同轴面齿轮系统弯扭耦合动力学模型,定义了系统动态均载系数计算方法,将计算方法的均载系数与TRP(technology reinvestment program)试验结果对比,验证均载计算方法的可靠性,开展齿轮支撑刚度对系统动态均载特性影响规律的研究。
1 系统弯扭耦合动力学建模
同轴面齿轮传动系统模型如图1所示,系统主要由输入齿轮1、惰轮2、输入齿轮3、惰轮4、下面齿轮5、上面齿轮6等组成。其中输入转矩通过两输入齿轮分流到上、下面齿轮,上面齿轮6为系统输出端,分流到下面齿轮5的转矩又通过两惰轮传递到上面齿轮6实现功率汇流。
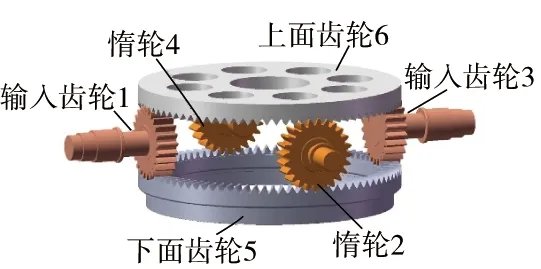
图1 同轴面齿轮传动系统
图2为系统弯扭耦合动力学模型。啮合副处及支承处的弹性变形用等效弹簧刚度表示,图中kUi表示上面齿轮6与输入齿轮、惰轮之间的轮齿啮合刚度,kLi表示下面齿轮5与输入齿轮、惰轮之间的轮齿啮合刚度;ku5、kv5、kw5分别表示下面齿轮5支撑处横向、纵向、轴向的等效弹簧刚度,ku6、kv6、kw6分别表示上面齿轮6支撑处横向、纵向、轴向的等效弹簧刚度;kui、kvi表示输入齿轮、惰轮支撑处横向、纵向的等效弹簧刚度。此系统共有(8+3×N)个自由度,其广义坐标如下:

图2 同轴面齿轮传动系统弯扭耦合动力学模型
X={θi,ui,vi,θ5,u5,v5,w5,θ6,u6,v6,w6}T
其中:θi为输入齿轮、惰轮扭转的微转角;ui、vi分别为输入齿轮、惰轮中心横向、纵向微位移;θ5为下面齿轮5扭转的微转角;u5、v5、w5分别为下面齿轮5中心横向、纵向、轴向微位移;θ6为上面齿轮6扭转的微转角;u6、v6、w6分别为上面齿轮6中心横向、纵向、轴向微位移;i=1,2,…,N,此系统N=4。
根据图2,由空间几何分析可得沿啮合线方向的位移:
(1)
式中:rbi为系统圆柱齿轮i(输入齿轮、惰轮)的基圆半径;rb5、rb6为上、下面齿轮等效基圆半径;eUi为圆柱齿轮(输入齿轮、惰轮)与上面齿轮6间的准静态传递误差;eLi为圆柱齿轮(输入齿轮、惰轮)与下面齿轮5间的准静态传递误差;φj为齿轮1与齿轮(j+1)轴线交角;i=1,2,3,4;j=1,2,3。
根据上述啮合线位移分析,可得各齿轮副间的动态啮合力为
(2)
式中:cUi表示上面齿轮6与输入齿轮、惰轮之间的等效啮合阻尼;cLi表示下面齿轮5与输入齿轮、惰轮之间的等效啮合阻尼;i=1,2,3,4。
根据图2动力学模型,可推得如下运动微分方程。
输入齿轮1:
(3)
惰轮2:
(4)
输入齿轮3:
(5)
惰轮4:
(6)
下面齿轮5:
(7)
上面齿轮6:
(8)
式中:mi为齿轮质量;Ii为齿轮转动惯量;FLj为圆柱齿轮(输入齿轮、惰轮)与下面齿5轮动态啮合力;FUj为圆柱齿轮与上面齿轮6动态啮合力;φk为输入齿轮1与齿轮(k+1)轴线交角;Ti为输入转矩;To为输出转矩;i=1,2,3,4,5,6;j=1,2,3,4;k=1,2,3。
2 系统动态均载计算方法
根据系统工作原理可知,两输入齿轮主要将输入转矩分流到上、下面齿轮,而输出端的上面齿轮6与输入齿轮及惰轮啮合实现转矩的汇流。
因此,定义输入端两输入齿轮与上、下面齿轮分支动力学均载系数为
(9)
输出端的上面齿轮6与两输入齿轮、两惰轮动力学均载系数为
(10)
令ΩP、ΩU为系统输入端与输出端的动态均载系数,则
(11)
式中:FiUR和FiLR分别为齿轮i与上、下面齿轮动态啮合力一个周期内的均方根值。
动态啮合力的均方根值可先通过MATLAB Simulink求得齿轮副动态啮合力,之后对一个啮合周期动态啮合力求均方值得到。动态啮合力均方根值可表示为
(12)
针对同轴面齿轮传动系统的均载特性,美国NASA曾在TRP计划中开展了试验研究[8],为验证提出的均载计算方法的可靠性,由该试验给定的齿轮参数和工况,开展了计算方法与试验结果的对比分析,结果如表1所示。齿轮模数为2,圆柱齿轮齿数为24,面齿轮齿数为97,输入功率为167 kW,输入转矩为200 N·m。

表1 均载结果对比
通过对比可知,本文提出的动态均载计算方法与试验最大相对误差为1.55%,说明利用该方法分析系统动态均载特性是可靠的。
3 动态均载特性分析
分析同轴面齿轮传动系统均载特性,齿轮基本参数及刚度参数分别如表2、表3所示。主要工况参数:输入转速600 r/min,功率0.6 kW。

表2 齿轮基本参数

表3 齿轮刚度参数 单位:N/m
基于上述参数,开展支撑刚度对动态均载系数影响规律分析,结果如图3、图4所示。
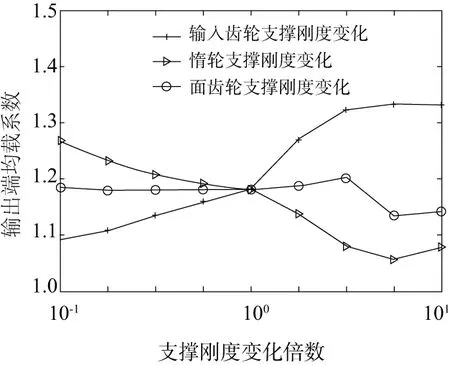
图3 齿轮支撑刚度对输入端均载系数影响
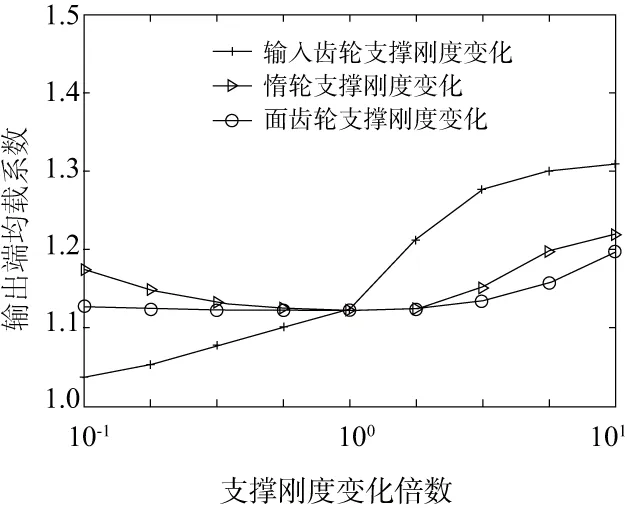
图4 齿轮支撑刚度对输出端均载系数影响
由图3可知,输入端均载系数ΩP随着输入齿轮支撑刚度的增大而变大,均载性能变差;输入端均载系数ΩP随着惰轮支撑刚度的增加而减小,均载性能变好;面齿轮支撑刚度变化时,输入端均载系数ΩP波动很小,均载性能变化不大。
由图4可知,输出端均载系数ΩU随着输入齿轮支撑刚度的增大而变大,均载性能变差;惰轮、面齿轮支撑刚度变化时,输出端均载系数ΩU波动很小,均载性能变化不大。
4 结语
本文建立了同轴面齿轮传动系统弯扭耦合动力学模型,定义了系统动力学均载系数计算方法,开展了支撑刚度对系统动态均载特性的影响分析,结论如下:
1)输入齿轮支撑刚度对系统输入、输出端均载系数均影响较大,适当降低输入齿轮支撑刚度有利于改善系统的均载性能。
2)惰轮支撑刚度对系统输入端均载系数影响较大,对输出端均载系数影响较小。
3)面齿轮支撑刚度变化对系统输入、输出端均载系数均影响很小,系统均载性能变化不大。
