基于现场总线的锅炉水给药预测及加药控制模型设计

王 昕

(三二○一医院工程科，陕西 汉中 723000)

0 引言

在热力发电厂中，由于锅炉水中pH值的变化，导致设备产生结垢和腐蚀等情况，对设备的安全和稳定带来了较大的损失[1]。因此，对于热力发电厂中的锅炉水进行一定的加药处理来对锅炉水的水质进行调整，而早期采用人工操作的加药处理中，锅炉水的水质参数与员工的操作熟练度有关，这种方法的控制效果不稳定[2]。

有学者在相关领域提出了自动控制下的加药控制方法研究，文献[3]提出了基于ARM处理器的污水加药控制方法，ARM处理器作为控制平台，降低了系统的功耗，结合加药控制，可以提高运行稳定性；文献[4]提出了基于CEPRM模型的锅炉水加药控制方法，基于CEPRM模型特点，对污水厂实际生产数据进行非线性拟合，优化了加药自控系统的设置要求与应用模式。但上述2种方法都没有将加药系统应用到锅炉水中，用以提高锅炉水的指标，而且这些方法的重点在于对加药参数按照加药规则表进行运算，缺少对加药后的水质变化预测，控制效果仍存在一定的局限性。

针对上述方法存在的问题，本文提出基于现场总线的锅炉水给药预测及加药控制模型设计。现场总线控制器的设计可将82C150控制器与上位机以及相关数据信息库进行连接，优化控制核心，使其更加快捷的执行全面控制。采用灰色预测方法预测给药动态信息，形成锅炉水的给药预测模型。通过预测模型对加药后水体的结果进行初步预测，满足要求后则进行加药操作，当预测结果没有满足要求时则将参数发回时滞加药内模中，通过这个循环形成加药控制流程。

1 基于现场总线的锅炉水给药预测及加药控制模型设计

1.1 现场总线控制器

为了方便执行全面控制，控制框架上选择了现场总线布置的方法[5]，利用CAN通信协议实现，在本文设计的控制方法中，选择采用82C150型号的CAN通信控制器[6]。该控制器温度范围为-40～+80℃，该总线控制器经过连接即可完成CAN总线的通信控制功能[7]，82C150总线控制器的引脚排列如图1所示。

图1 82C150引脚排列

在图1中，引脚P1以及引脚P2均为负编程的输入端口；Vss1为逻辑电路和驱动器的连接口；Vss2为设备输入和振荡器接入点；VDD1为逻辑电路和82C150的电源连接点；VDD2为设备输入和振荡器的电源连接点；P0为标识符编程的输入端；P14为复用模拟信号接入端口；P15为A/D比较器输入接口；其余P口均为比较器的同相接入点。在整体上可以利用I/O驱动将82C150控制器与上位机以及相关数据信息库进行连接。利用82C150对相连接的设备进行统一调控，实现总线控制。

1.2 时滞加药内模参数修正

内模控制是通过数学算法以及动态矩阵的一种控制策略，通过动态矩阵对加药参数进行修正[8]。而在内模控制中，需要一个整定参数来对参数进行调整，并保证鲁棒关系[9]，内模控制原理结构如图2所示。

图2 内模控制原理结构

图2中，Gc为控制模式中的控制器；Gp为被控对象模型；Gm为过程模型；U(s)为经过被控对象后的控制需求输入函数；d(s)为鲁棒函数。而在图2中显示的控制输入以及输出间的传递函数为

(1)

Y(s)为获得控制后的输出函数；R(s)为被控对象的输入。获取的反馈信号则为

B(s)=[Gp(s)-Gm(s)]U(s)+d(s)

(2)

对内模控制器Gc(s)定义为

(3)

f(s)为控制器中的可实现因子，同时也为内部的滤波器。而在进行加药过程中，对其内模的控制还应考虑到加药中的大滞后和非线性对象。在进锅炉水中的水汽，经过取样管，并引入取样架内时，进行降温降压处理，在将水流经过仪器进行检测，时间上会产生滞后现象，这种现象叫作传输滞后[10]。而对检测部位取样，对取样分析时的时间，叫作滞后时间[11]。而在锅炉水被加药后，其中的水体参数需要经过药物的化学反应才会发生变化，这也就导致了在该过程中存在一定的惯性以及滞后性[12-13]。由于存在滞后性，导致进行加药控制时，收到信号后，无法实现即时的反应，导致输入以及输出的数值上存在一定的差异性[14]。定义τ为滞后时间；y(t)为在锅炉水的加药控制中输出指令；r(t)为输入指令。则可导出

y(t)=r(t-τ)

(4)

在加药控制中，将加药的条件概况在广义对象中，此时的广义对象则可以以纯滞后的形式来表示，即

(5)

K、T和τ为控制中的增益时延，在加药控制方法中，将内模控制的运算，作为一个高阶运算过程，并使其中的参数随着时间和外部干扰等因素进行变化[15]。由于应用了现场总线进行控制，因此控制结构属于线性闭环控制，滞后将根据所处的不同位置对控制结构产生不同的影响，可表示为

(6)

k(s)为加药调节设备的传递函数；G0(s)为过程中被控制对象(代表加药量)的传递函数；H(s)为测量变送器的传递函数。根据式(6)，在k(s)、G0(s)和H(s)中当任何位置出现了纯滞后现象后，则

1+k(s)G0(s)H(s)=0

(7)

在式(7)中可以发现，当整体控制环境中的通道内出现纯滞后现象，整体的控制结构中的纯滞后时间则会增大，且干扰通道滞后对特征方程无影响[16]。但纯滞后则会影响控制结构的性能，而此时结构的频率特性为

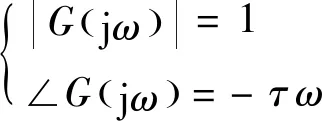
(8)

根据式(8)中结果得知，在出现滞后现象后，在幅相频特性中，滞后的相角和ω呈正比，同时滞后现象中，其相位滞后受τ值大小的影响。当结构处于低频周期性扰动时，其响应将会更加灵敏，同时为了提高控制结构的稳定性，需要对相关控制器中的增益降低，并使其最大偏差加大。在滞后时间τ增加时，其滞后相角会处于无限大。而对控制质量来说，控制质量也与过程中的惯性常数有关，因此在实际的控制工作中，当T值较大时，即使τ值较大，其控制结构仍然处于稳定。

1.3 给药预测模型

锅炉水加药处理过程中，因为锅炉水进行热传递时会有延迟，所以导致对加热目标进行加药时会有细微的迟滞性。致使控制系统不可以正确追踪输入量，使系统稳定性遭到破坏[17]。

当前方法对滞后性造成的问题往往没有较好地解决方案，致使加药过程没办法依靠动态特性随时调节，关于那些非线性变化过程的控制成果不佳。往往需要反馈回路对滞后因子进行补偿，使其能够准确地跟踪系统的输入量。

在给药过程中，锅炉水中的成分含量可以看作一个动态信息，该信息反映着加药控制的质量。而选择采用灰色预测来对给药动态信息进行预测，并建立目标微分方程模型。其中,灰色预测GM(1,1)模型的原始序列为

X(0)={x(0)(1),x(0)(2),…,x(0)(n)}

(9)

X(0)为模型中的原始序列，它有较多随机性，因为灰色量有缺失，所以需要弱化原始序列的随机性，产生新序列；k为时间序列。建立GM(1,1)灰度方程为

(10)

而对GM(1,1)的白化微分方程为

(11)

获得式(11)的解为

(12)

(13)

B为其中的数据阵；γN为其中的数据列。经由GM(1,1)模型进行累加，根据所建模型获取得到预测值

(14)

k=1,2,…,n-1

加药过程中，需要依靠加药控制精度的需求来确定量化等级，量化等级越高，对加药控制精度的需求也会越大。所以在加药控制精度能力内，尽量去提高量化等级。

1.4 加药控制模型

通过预测值来对当前给药后的参数进行预测，给药时的控制过程如图3所示。

设计的加药控制方法流程如图3所示，通过预测模型对加药后水体的结果进行初步预测，满足要求后则进行加药操作，当预测结果没有满足要求时则将参数发回时滞加药内模中，对加药的参数进行修正，将控制器中输入变量的个数作为加药控制系统的维数，采用控制器对加药控制系统控制时，输入变量值的个数选取会影响加药控制系统的动态性能。因此需要将误差的变化值也作为输入参数的一部分，考虑到控制规则是通过手动规则来提出。在内模控制器中，可根据手动输入变量来确定3种内模控制输入变量，即输入的误差数据、输入的误差变化值以及误差变化平均值数据，并以实际过程中的控制量变化作为内模控制的输出变量。

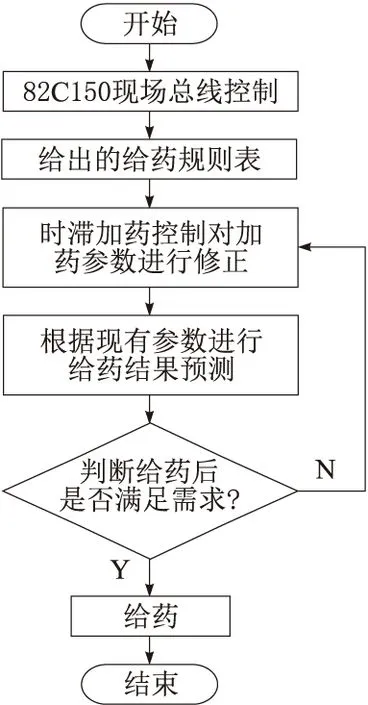
图3 加药控制流程

控制中容易产生振荡，导致误差处于零值，在分区段上，所输入的误差以及对应的误差变化均属不同条件下，根据相应的误差即可获得加药参数修正后的加药控制规则。而当其输入以及输出的变量得到确认后，得到隶属函数，依据实际情况选择对应数值，写出相关的变量赋值表，对控制结构的误差变化率以及控制量进行赋值，实现加药控制。

2 实验论证分析

为了验证设计的给药预测及加药控制方法的有效性，对某锅炉水处理车间中进行应用实验，并测试设计的给药预测及加药控制方法是否可以实现对锅炉水加药参数的控制，来保证锅炉水中成分满足相应需求。

2.1 实验锅炉水加药原理

由于锅炉中原水的硬度较高，因此需要降低原水汇总的硬度。空气中的O2会进入锅炉水中，与锅炉水中的H2O和Fe进行化学反应，而其中CO2会让锅炉水中的食盐溶液变成酸性，为了保证安全运行需要去除其中的CO2以及O2。而实验中的锅炉水加药选择通过添加氨来提高凝结水的pH值，其中pH值过低则会导致金属受到酸性水体的腐蚀，而过高则会引起碱性腐蚀，因此,实验中的给药控制需要将pH值设定在规定范围内。实验中加药设备流程如图4所示。

图4 设备加药流程

为了避免实验锅炉中锅炉水对锅炉的腐蚀，根据该锅炉水处理车间中的特定水况，对其pH值的测定范围设为8.8～9.4，对其联氨测量范围为12～33 μmol/L。

2.2 实验结果

采用基于现场总线的锅炉水给药预测模型对锅炉水处理车间中的锅炉水进行给药预测。将预测数据和实际变化结果相互对比，结果如图5所示。

图5 实际联氨和预测结果

从图5中可以看出，对其中成分变化的预测运算与实际结果较为贴合，实际变化结果在40 min内联氨含量最大值为34.05 μmol/L，联氨含量最小值为17.82 μmol/L；预测结果在40 min内联氨含量最大值为33.85 μmol/L，最小值为17.95 μmol/L。证明本文设计的加药预测方法具有较高的可行性。

为了进一步证明设计方法的性能，采用上述预测结果控制锅炉给药过程。实验中对锅炉给药的时刻监测结果如表1所示。

表1 锅炉给药过程实时监控记录表

在表1中发现，除去00：00：00时间点的检测结果外，其余结果中的pH值以及联氨范围值均处于允许范围中。这是因为该系统采用给药预测及加药控制方法，形成循环加药控制流程，可以更好的控制加入锅炉内的给药量，从而控制其pH值。而00：00：00时间点为实验开始时间，因此检测出的数据为给药前的锅炉水数据。

3 结束语

在对锅炉水的给药预测及加药控制中，设计了对加药后的相关预测计算，并使用现场总线实现全局控制，提升了加药控制性能。给药预测实验结果表明，该方法的预测准确率较高，可行性高；据此对锅炉给药过程实时控制，通过锅炉给药过程实时监控记录表可以看出，本文方法可以较好的控制锅炉内的pH值，证明了所提加药控制模型的准确性。

但在本研究中，由于采用了灰色预测，且预测运算中存在较多的矩阵运算，需要建立上位机的运算结构，但该结构在上位机故障的情况下，会影响整个控制方法的运行，因此可靠性较低，在未来研究中仍需进一步改进。