空调电机启动控制设备变形量激光检测方法

刘明会，张滨娜

(吉林大学中日联谊医院南湖院区，吉林 长春 130012)

0 引言

随着工业技术的迅猛发展，机械制造业正在朝着大规模集成化以及自动化方向进行转变[1-2]，对现阶段已有的空调电机启动控制设备提出了更高的要求。相关统计数据显示，空调电机在运转的过程中，需要消耗的能量[3-4]大约占整个工业的70%，这在一定程度限制了经济的发展。另外，更不容忽视的问题就是空调电机启动控制设备变形量激光检测问题，现阶段相关专家已针对该方面的内容进行了研究[5-6]，但有的方法导致漏检率增加，有的方法导致虚警率大幅度增加。为了有效解决上述问题，提出一种基于MNF的空调电机启动控制设备变形量激光检测方法。

1 检测方法

1.1 基于MNF的空调电机启动控制设备图像去噪

采用激光扫描技术对空调电机启动控制设备进行扫描，获取空调电机启动控制设备图像。完成扫描之后，需要进一步分析空调电机启动控制设备图像中存在噪声对图像质量产生的影响。另外，设定信噪比为度量的最小噪声分离变换，通过其实现图像成分分解。

为了进一步实现MNF变换[7-8]，最为核心的步骤就是针对图像中存在的噪声进行估计，同时得到对应的噪声协方差矩阵。以下详细给出MNF变换的具体操作步骤。

a.将空调电机启动控制设备图像中包含的全部噪声进行高斯滤波处理，获取噪声协方差矩阵Σn。

b.计算确定的噪声协方差矩阵Σn的特征值以及特征向量P。将特征值组成对角矩阵[9]，将其表示为Δ，由P组成的矩阵记为E。

c.获取Σn的白化矩阵F，即

(1)

d.获取观测数据FTZ的协方差矩阵，即

(2)

e.利用Σn获取特征值以及特征向量，将全部的特征值组建对角矩阵Λ，其中对应特征向量组成的矩阵为G。

f.将G作用到FTZ的各个像元上，GTFTZ为经过MNF变换后得到的图像[10]。根据上述过程，得到MNF变换操作流程如图1所示。

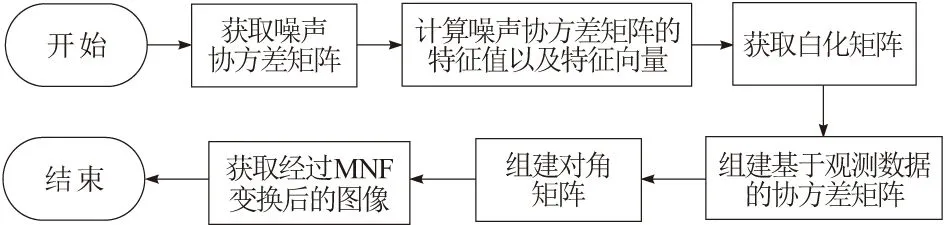
图1 MNF变换操作流程

考虑到MNF变换后的特征向量均是单一存在的，其会导致图像的质量受到一定程度的影响[11-12]。为了有效解决上述问题，需要将全部信噪比按照从大到小的顺序进行排列，这样不仅能够有效克服噪声，同时还能够提升图像的质量。

在传统的MNF变换中，噪声是通过线管与相邻点的差值来估计空调电机启动控制设备图像的数据噪声。然而，大多数图像中的噪声是随机的，它们可以是椒盐噪声，也可以是条带噪声，或者两者兼有。为了有效弥补MNF变换的局限性[13]，采用加权邻域平均法估计噪声矩阵，并给出目标像素区域8个像元的相同值，如图2所示。

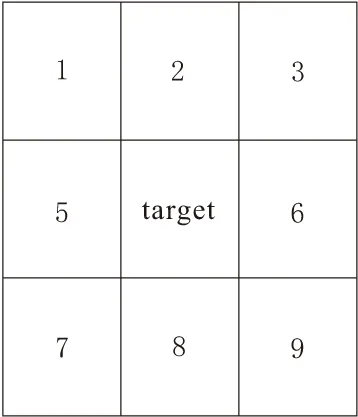
图2 去噪窗口示例

以图2所示去噪窗口为基础，得到各个像素到均值像素之间的倒数距离值，其表示形式为

(3)

ri为图像中不同像素点的光谱数量；p为背景检测过程中光谱总数，即

(4)

邻域差值为

(5)

其中不同像元处的差值为

ΔX=ri-pw

(6)

结合上述分析，主要通过ΔX对噪声进行评估。

设定空调电机启动控制设备图像目标的向量为r，背景的均值向量为μ，背景的协方差矩阵为C，则

(7)

RΔX为单一空调电机启动控制设备中像元的检测结果。在上述分析的基础上，分别给予邻域内各个像元一个特定的取值，有效增强背景像元在领域矩阵的比例值，有效抑制噪声[14]。同时，还需要结合差值有效提取空调电机启动控制设备图像中的噪声信息，利用改进的MNF变换有效实现图像降维以及去噪处理。

1.2 空调电机启动控制设备变形量激光检测

整个空调启动装置的图像元素可以分为2种不同的类型：异常和背景。假设获得图像中的部分模糊监测信息，可以有效控制后续的变形数据提取过程，导致图像中特征类别的增加。因此，设定空调电机启动控制设备图像为X。同时，设定Xk为第k个波段图像；L为图像中各个变形量的波段总数[15]；xi为第i个像元；N为像元的总数。单一空调电机启动控制设备中像元的检测结果为RΔX(xi)，xi为异常成分的概率和RΔX(xi)呈正相关，则具体的计算公式为

(8)

exp为高斯径向基函数；σ为对应的参数。由于在空调电机启动控制设备图像中，变形量像元数量占总数的10%，所以需要将全部的像元值进行排序[16]，同时选取大约5%的RΔX(x)值赋予给σ。

结合式(9)计算2个空调电机启动控制设备中2个像元之间的类别相关属性Psimij。其中，Psimij的取值越大，则说明2个设备之间的变形量属于相同类别的概率就越大。

(9)

xj为设备2的第j个像元。在空调电机启动控制设备中，以像元为单位排列成近似线性几何结构，具有以下优点：

a.隶属于相同类别的概率比较接近，即Psim的取值更加接近于1。

b.像元之间的距离较小，则2个空调电机启动控制设备之间的距离计算公式为

(10)

在此基础上，介绍了等距邻接图的生成方法G1。

通过式(11)对G1中的近邻系数G1ij进行初始化处理，像元xi和xj属于同一类别，并根据区域的可能性和G1ij大小，具体的计算公式为

G1ij=Psimij(1-dij)

(11)

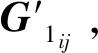
为了最小化同一类型特征邻域像元之间的距离，有效减少像元之间的类内散射[17]，主要通过式(12)对目标函数进行优化处理，即

(12)

y为像元x的特征提取结构。

基于以上分析，为了使特征数据具有更高的空间分辨率，有效防止像元修改引起的数据结构的显著变化，引入了特征等距显示的思想，以充分利用原始数据的流线型全局结构[18]。设定I为N×N的单位矩阵，E为N×1的全1向量，其中：

(13)

(14)

(15)

(16)

为了消除目标函数存在的弊端，需要对其进行线性化以及核化处理，以下给出具体的操作步骤。

a.线性化。

设定Y=AT·X，其中AT为L·Q线性映射矩阵，将Y代入到式(16)中，则有

I=ATXXTA

(17)

将式(17)进行转换，则能够获取以下的广义特征值方程，具体的表现形式为λXXTA。

针对全新的数据x′，能够获取对应的特征提取结果y′，即y′=AT·x′。

b.核化。

利用核函数将像元xi进行非线性映射，同时采用Ker(xi,xj)代表像元Φxi和Φxj之间的内积，获取广义特征值方程，即λΦ(X)Φ(X)TA。

在上述分析的基础上，结合激光检测技术对空调电机启动控制设备进行变形量检测，具体的计算公式为

(18)

综上所述，完成空调电机启动控制设备变形量激光检测。

2 仿真分析

为了有效验证本文基于MNF的空调电机启动控制设备变形量激光检测方法的有效性，分别使用文献[5]的一种真圆型隧道激光扫描断面变形检测新方法和文献[6]的基于三维激光扫描技术的油罐变形检测方法，进行仿真对比测试。

a.漏检率。漏检率可以反映不同方法正确识别空调电机启动控制设备变形量的准确率，为此，以换向器直径为测试指标，对比3种不同检测方法的换向器直径变化量。在换向器中标注5个易发生变形位置的监测点，分别对比动压成形后不同方法的换向器直径误差，漏检率越高，直径误差越大，具体对比结果如图3所示。

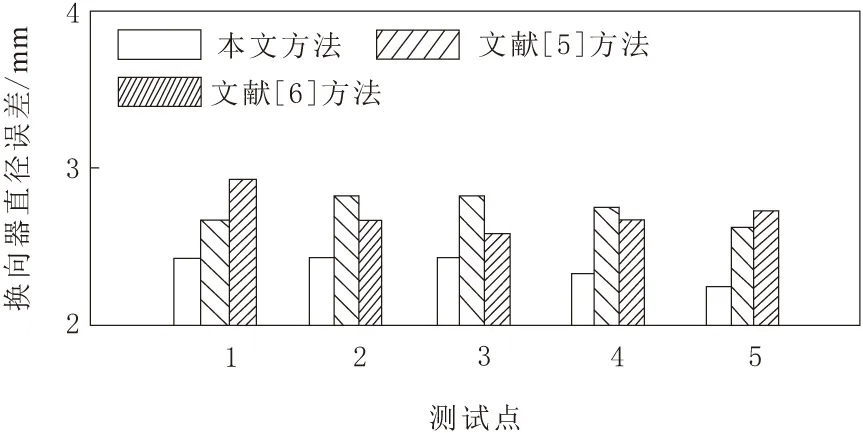
图3 不同检测方法的换向器直径误差对比

分析图3中的实验数据可知，由于监测点不同，导致各个检测方法的换向器直径误差也在不断发生变化。但是在实际应用的过程中，所提方法对空调电机启动控制设备图像进行去噪处理，促使整个方法的换向器直径误差明显低于另外2种方法，提高了漏检率。

b.虚警率。为了验证本文方法检测效果的可比性，进一步对比不同检测方法的虚警率。该指标通过空调面板翘曲程度进行测试，翘曲程度测试值越高，证明对应测试方法下受噪声干扰影响程度较小，由此得到具体的对比结果如表1所示。

表1 不同检测方法的空调面板翘曲对比

分析表1中的实验数据可知，本文方法有效解决了空调电机启动控制设备图像的去噪问题，促使整个方法有效避免外界干扰，空调面板翘曲程度下降，明显低于另外2种检测方法，同时也充分验证了本文方法检测结果的优越性。

3 结束语

针对传统检测方法存在的一系列问题，设计并提出一种基于MNF的空调电机启动控制设备变形量激光检测方法。仿真结果表明，本文方法能够有效降低漏检率和虚警率。