圆钢管柱变形性能研究
2021-12-26柴会娟陈宇辰张康伟李振宝张广平薛海龙秦启运
范 重,柴会娟,陈宇辰, ,张康伟,李振宝,张广平,薛海龙,秦启运,何 韬
(1. 中国建筑设计研究院,北京 100044;2. 中冶建筑研究总院有限公司,北京 100088;3. 北京工业大学工程抗震与结构诊治北京市重点实验室,北京 100022;4. 雄安高速铁路有限公司,保定 071700)
在航站楼、体育场馆等大型公共建筑中,根据建筑人流密集、空间高大和技术经济性要求等特点,一般其下部主体结构采用钢筋混凝土框架、上部大跨度屋盖采用钢结构的方式.与钢筋混凝土柱相比,钢管柱自重轻,承载力高,变形能力强,施工方便.支承大跨度屋盖的钢管柱,既可以通过抗震球形支座与屋盖结构相连,也可以通过在柱顶设置V 形斜撑与屋盖结构相连.钢管柱底部与框架结构刚接,顶部与大跨度结构通常为铰接,受力形态接近于悬臂柱[1].
现行国家标准仅对钢框架在水平荷载作用下的层间位移角限值做出了明确规定,根据《钢结构设计标准》(GB 50017—2017)[2]和《建筑抗震设计规范》(GB 50011—2010)[3],钢框架在风荷载和多遇地震作用下的弹性层间位移角不宜超过1/250,罕遇地震作用下的弹塑性层间位移角不宜超过1/50.对于支承大跨度屋盖的钢管柱,其受力状态与排架柱较为接近,轴压比较小,侧向刚度通常起控制作用,如果直接套用现行国家标准对钢框架层间位移角限值的规定,可能导致设计偏于保守,导致钢的用量明显增大.此外,当大跨度屋盖的高差较大时,屋面较低部位的钢管柱常常难以满足规范变形角限值的要求.
近年来,国内外学者对钢管柱的抗震性能进行了较为深入的研究.Mamaghani 等[4]在进行圆钢柱弹塑性有限元分析时,采用修正拉格朗日方程描述几何非线性,通过双屈服面本构模拟材料非线性,计算结果与试验符合良好.Gao 等[5]通过非线性有限元分析与模型试验,对钢桥圆管柱在往复荷载作用下的承载力与延性进行了研究,考察了钢材本构关系、长细比、径厚比以及加载次数的影响.Goto 等[6]对薄壁柱在往复荷载作用下的屈曲形态与滞回性能进行了研究.Elchalakani 等[7]通过冷成型圆管往复弯曲试验,考察了长细比对构件刚度、局部屈曲和延性的影响.Goggins 等[8]通过对方、矩形截面支撑进行往复与单调轴向加载试验,考察冷弯箱形构件长细比以及截面特性对承载力、屈曲与横向变形、延性以及耗能性能的影响.王开飞等[9]采用ANSYS 有限元软件,对圆钢管压弯构件的极限承载力、延性系数与滞回特性进行数值模拟,研究了长细比、径厚比与轴压比等参数对圆钢管滞回性能的影响,并与试验结果进行了比较.苏明周等[10]对15 个箱形试件进行常轴力、循环往复弯矩作用下的试验研究,考察了轴压比和宽厚比对箱形柱滞回性能的影响.范重等[11]针对大跨度箱形构件用钢量较大的问题,提出一种带加劲肋的薄壁箱形梁,采用有限元分析软件建立了计算模型,对屈曲模态、承载力、变形性能、耗能能力和损伤情况进行了研究.
应当指出的是,由于支承大跨度屋盖钢管柱的轴压比较低,迄今针对钢管柱变形能力、尤其是低轴压比钢管柱变形性能的研究还很少.此外,结构层间位移角限值除了受到构件变形能力的影响外,还受到围护结构性能以及电梯运行要求等很多因素的影响.砌筑填充墙变形能力较差,人造板材和轻钢龙骨板材等轻质隔墙适应变形的能力较强.玻璃幕墙、石材幕墙对结构变形要求较为严格,而金属幕墙、轻质复合墙体对结构变形要求可以放松[12-13].
本文针对支承大跨度屋盖钢管柱的受力特点,进行了3 个低轴压比钢管柱在水平往复荷载下的模型试验,考察径厚比、长细比对试件变形能力与破坏形态的影响.采用ABAQUS 非线性有限元软件[14]对钢管柱试件往复加载过程进行模拟,确认有限元分析方法的可靠性.采用有限元法对钢管柱在往复荷载作用下的承载力与变形性能进行分析,分别考察长细比、径厚比和轴压比对钢管柱屈服变形角和极限变形角的影响.在此基础上提出了钢管柱在多遇地震与风荷载及罕遇地震作用下变形角限值的设计建议.
1 钢柱模型试验
1.1 试件设计
结合大跨度屋盖设计对钢管柱变形能力的需求,在北京工业大学工程抗震与结构诊治北京市重点实验室进行了钢管柱在往复荷载作用下的力学性能试验,考察其承载力、变形性能、滞回曲线与耗能性能,为大跨度结构设计时钢管柱变形角控制提供依据.
本次试验共有3 根钢管柱试件,钢材材质均为Q345B,圆钢管采用坡口熔透焊缝.试件的几何参数如表1 所示,轴压比约为0.2.

表1 试件基本信息Tab.1 Basic information of specimens
试件顶板平面尺寸为400 mm×400 mm,厚度为20 mm;底板平面尺寸为590 mm×650 mm,厚度为50 mm.为确定钢材的力学特性,从试件上取样进行材性试验,得到试件钢材的力学性能如表2 所示.

表2 试件钢材的力学性能Tab.2 Mechanical properties of specimens’ steel
1.2 试验装置与加载方案
试验采用反力架加载系统进行拟静力加载,通过1 000 kN 的MTS 数控电液伺服作动器施加水平往复荷载,作动器一端固定在反力墙上,另一端通过高强螺栓与柱顶的加载板相连.加载端头一侧与作动器相连,另一侧通过螺杆和夹持板相连,并将钢管柱牢固夹持,以保证水平荷载的作用点尽量在钢管柱中心.柱顶端采用2 000 kN 液压千斤顶施加恒定竖向压力,千斤顶固定在有滑轮的滑板上,当作动器反复推拉试件时,千斤顶可以随试件移动,以保证施加轴力作用点始终位于钢柱顶部加载板中心.试验加载装置见图1.
加载底座通过4 个锚固螺栓固定于地面,保证底座与地面之间不会发生相对滑移.为方便作动器、加载端头及夹持板可靠连接,在圆钢管柱中上部设置两块连接板.在柱下设置平面尺寸为 3 400 mm×650 mm×500 mm、厚度为50 mm 的底板,钢柱底板通过高强螺栓与底座顶板相连,满足钢管柱底部为嵌固的边界条件.
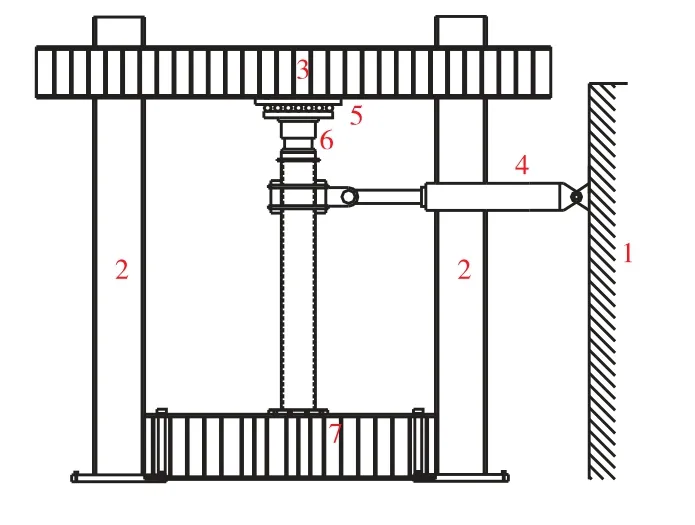
图1 试验加载装置Fig.1 Test loading setup
试验过程中,首先对试件施加轴向荷载,在试验过程中竖向荷载保持恒定.根据《建筑抗震试验方法规程》(JGJ 101—2015)[15]的相关要求,往复加载采用荷载、位移分阶段混合控制的加载制度.试件屈服前为荷载控制阶段,分别以屈服荷载的 10%、20%、30%直至100%进行分级加载,每级荷载循环1次;试件屈服后,改为位移控制加载,分别以Δy、2Δy、3Δy、4Δy,…,进行加载,其中Δy为屈服时柱顶的水平位移,每级加载循环3 次,直至荷载下降至低于峰值荷载的85%或试件破坏严重时,结束加载.试验采用的加载制度如图2 所示.

图2 往复试验加载制度Fig.2 Cyclic test loading system
1.3 测点布置
在钢管柱低周反复试验中,采用DH801-750 型拉线位移计测量柱顶的水平位移和竖向位移,YHD-100 型位移计测量底座的水平位移.
位移计和应变仪的布置情况如图3 所示(括号中的数字仅用于试件P-4),分别在底座顶面和钢柱底板设置位移计①和②,用于检测柱底竖向位移以及钢柱与底座之间的相对滑移;位移计③和④距钢柱底板300 mm 处,用于测量塑性铰区的弯曲变形;位移计⑤和⑥用于测量在加载标高的水平位移并监测加载过程是否存在外倾或扭转;在距钢柱底板350 mm 范围内,分别在荷载作用方向以及垂直荷载作用方向钢管表面布置双向应变片.在试验过程中,力、应变和位移等通过IMP 数据采集系统进行实时采集.

图3 试件测量装置布置Fig.3 Arrangement of measuring instrument on specimen
1.4 试验结果与分析
1.4.1 破坏过程及现象
3 根钢管柱在恒定轴压、低周反复加载过程中,均经历弹性、弹塑性和破坏3 个阶段.从开始加载到钢管柱根部进入屈服之前,各试件处于弹性阶段,水平力与柱顶位移总体上呈线性关系.进入屈服后,各试件破坏过程具体如下.
试件 P-1 进入屈服后,加载至 94.5 mm(θ=1/31.7)变形角时,试件距根部70 mm 高度发生环形外鼓,但程度尚不显著.在其后加载过程中,外凸变形逐渐发展.当试件达到最大承载力后,外凸变形继续发展,但荷载基本保持不变或稍有降低.加载至130 mm(θ=1/23.1)时,最大鼓出变形达30 mm,承载力下降严重,停止加载.P-1 的破坏形态如图4 所示,钢管鼓曲变形显著,主要位于底板以上50 mm 的范围.

图4 P-1试件破坏状态Fig.4 Failure pattern of specimen P-1
试件P-3 进入屈服后,加载至120 mm(θ=1/25)时,试件根部70 mm 高度处出现环状鼓曲,程度不明显.在其后加载过程中,外凸变形逐渐发展.试件达到最大承载力后,外凸变形不断发展,但荷载基本保持不变或稍有降低.加载至260 mm(θ=1/11.5)时,承载力逐步下降,但由于设备原因,未能继续往下加载,停止加载.试件P-3 的破坏形态如图5 所示,由于其径厚壁大于试件P-1,钢管鼓曲变形较为平缓,主要位于底板以上100 mm 的范围.

图5 P-3试件破坏状态Fig.5 Failure pattern of specimen P-3
试件 P-4 进入屈服后,加载至 22.5 mm(θ=1/53.3)时,试件根部60 mm 高度处出现环状鼓曲,程度不明显.在其后加载过程中,外凸变形逐渐发展.试件达到最大承载力后,外凸变形继续发展,但荷载基本保持不变或稍有降低.加载至52.5 mm 第3循环(θ=1/22.9)时,试件两侧根部均出现裂缝.加载至60 mm(θ=1/20)时,听到清脆响声,试件两侧根部发生断裂,承载力下降严重,停止加载.试件P-4 的破坏形态如图6 所示,钢管鼓曲变形较为平缓,主要位于底板以上100 mm 的范围.

图6 P-4试件破坏状态Fig.6 Failure pattern of specimen P-4
1.4.2 滞回曲线与承载力
钢管柱试件的水平荷载-变形角滞回曲线如图7所示,其中,横坐标为试件加载部位的变形角(θ=Δ/h),纵坐标为施加在试件上的水平力P.
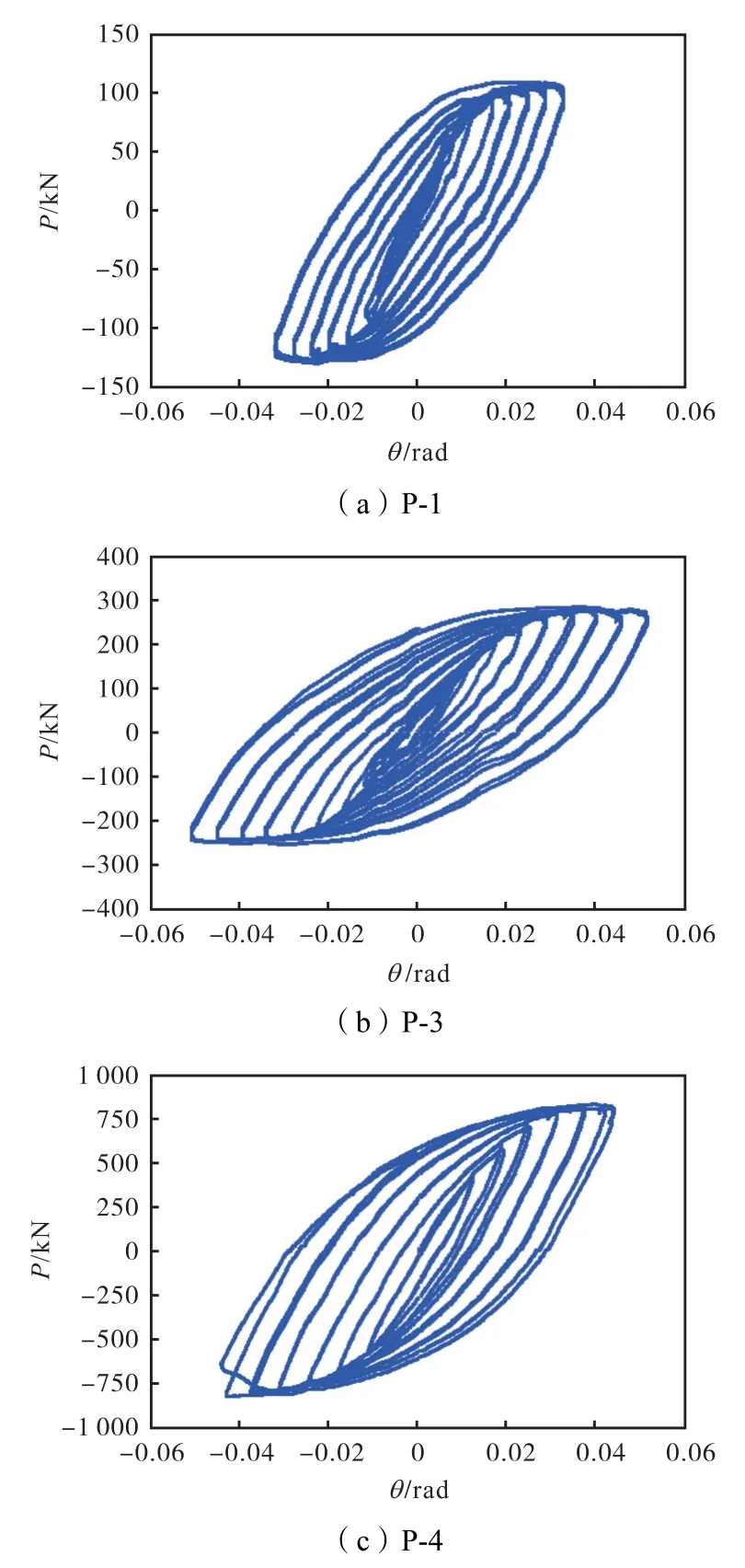
图7 钢管柱试件的荷载-变形角滞回曲线Fig.7 Load-deflection angle hysteretic curves of pipespecimens
由图7 可知,滞回曲线均呈较为饱满的梭形,表现出良好的耗能能力.加载初期,柱顶水平位移较小,试件处于弹性阶段,侧向刚度较大;随着加载位移增大,钢管逐渐进入屈服,承载力随位移增大的变化幅度较小;对于同级加载,除P-1 停止加载前之外,后2 次循环加载时的承载力均与第1 次较为接近,表明试件在往复荷载作用下管壁弯曲变形的影响较小.
试验得到的钢管柱的特征承载力、相应的变形角及延性系数见表3.其中,屈服荷载根据骨架曲线采用能量等值法确定,极限变形角为承载力降至最大承载力85%时相应的变形.从表中可知,本次试验轴压比为0.2 左右,钢管柱的屈服变形角远大于1/250,极限变形角均能大于1/30;径厚比越小、长细比越大,其变形能力越强,延性系数越大.
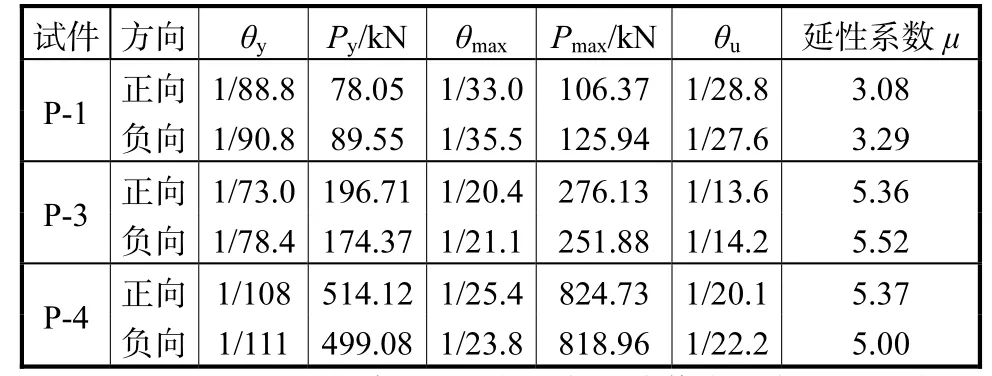
表3 试件的特征承载力、变形角与延性系数Tab.3 Characteristic load,drift angle and ductility factor of specimens
1.4.3 耗能性能
本文以等效黏滞阻尼系数ζeq表征试件的耗能性能,计算方法见式(1)和图8.
式中:SAFCDA为一个滞回环所包围的面积;SCPB、SAEP分别为三角形CPB、AEP的面积.
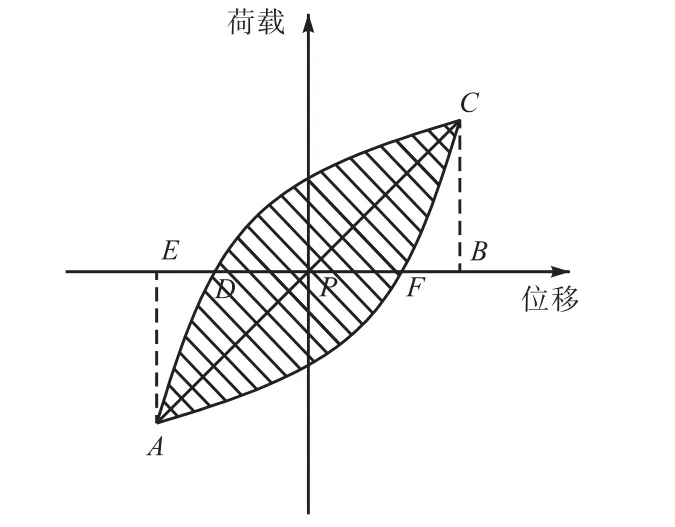
图8 等效黏滞阻尼系数计算示意Fig.8 Calculation of equivalent viscous damping coefficient

钢管柱试件在加载过程中等效黏滞阻尼系数随变形角的变化情况如图9 所示.
从图9 中可以看出,3 个试件黏滞阻尼系数的发展过程类似,屈服前黏滞阻尼系数很小;试件屈服之后,滞回环面积增大,等效黏滞阻尼系数随之增加.试件P-1 径厚比较大,等效黏滞阻尼系数增长最快,表明其塑性变形发展最快,损伤程度严重;试件P-3 径厚比较小,塑性变形发展缓慢,但耗能能力最强;试件P-4 径厚比与试件P-3 相同,但长细比减小,其塑性耗能性能略逊于试件P-3.
2 有限元模拟与试验结果比较
2.1 计算模型
本文采用ABAQUS 非线性有限元分析软件[14]对钢管柱试件进行计算分析.柱身钢管采用S4R 壳单元进行模拟,单元网格尺寸为20 mm.柱底为固结边界条件,将柱顶耦合至柱顶截面形心,在形心施加轴向压力和往复水平位移.计算分析时采用与试验相同的轴力,水平加载制度与前述模型试验相同.
钢材弹性模量E=206 kN/mm2,泊松比ν=0.3,钢材强度根据表2 的试验结果确定.范峰等[16]通过对圆钢管进行三向加载试验,得到考虑损伤和裂纹影响的材料损伤累积本构模型,用于考察单层球面网壳在地震作用下的响应.本文钢材本构模型采用随动硬化本构模型[17],利用ABAQUS 软件中的cycle hardening 材料属性,对循环荷载作用下钢材的本构关系进行模拟,具体参数见表4.此外,通过在钢管柱底部预设低阶屈曲模态的方式,模拟初始缺陷的影响.
2.2 有限元分析结果
2.2.1 滞回曲线与骨架曲线
非线性有限元分析与模型试验所得钢管柱承载力与位移的比较见表5.从表中可知,有限元计算得到的屈服荷载与最大承载力与模型试验结果较为接近,但屈服位移、最大承载力相应位移以及极限位移相对误差较大.这是由于钢管柱试件尺寸较小,初始缺陷与焊接残余应力的影响较大,有限元模型难以考虑相关因素,故此有限元模型侧向刚度较大,位移计算结果较小.
有限元分析得到试件的荷载-位移曲线与骨架曲线如图10 所示.由图可知,有限元分析结果与模型试验结果总体上较为一致.
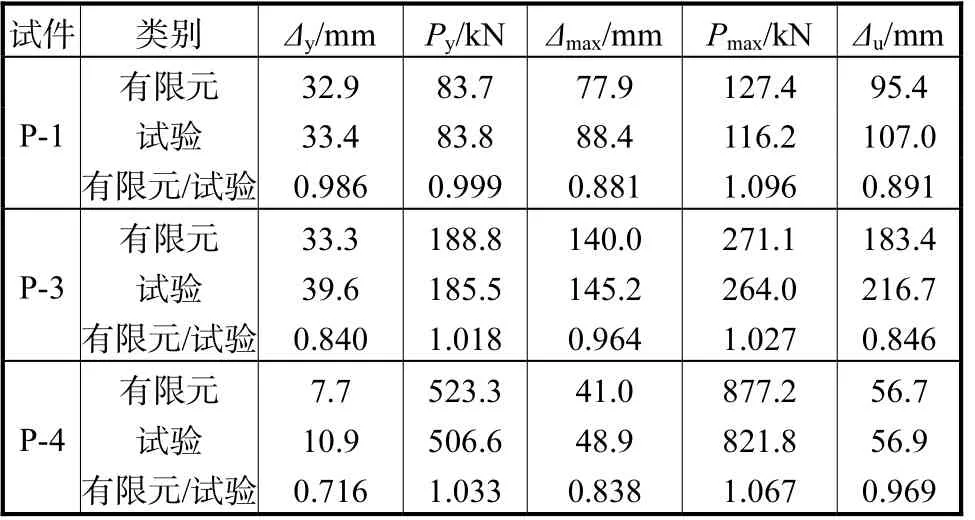
表5 有限元分析与模型试验承载力与变形的比较Tab.5 Comparison between bearing capacities and deformations by FEM analysis and experiment
2.2.2 破坏形态比较
在往复荷载作用下,有限元分析得到钢管柱试件结束加载时的破坏形态如图11 所示.由图可知,有限元分析得到试件底部侧壁的变形情况与试验结果基本吻合,验证了非线性有限元分析结果的可靠性.
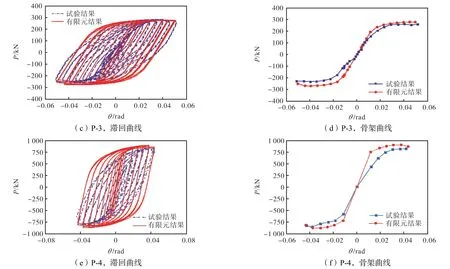
图10 有限元分析与模型试验结果的比较Fig.10 Comparison between FEM analysis and experiment results

图11 试件破坏形态对比Fig.11 Comparison of specimen failure patterns
3 钢管柱变形能力研究
3.1 有限元模型与计算参数
在对钢管柱变形能力进行计算分析时,假定圆钢管的直径D=1 200 mm,钢材材质为Q345.根据工程中钢管柱的应用情况,确定轴压比n、径厚比D/t和长细比λ等参数的变化范围如表6 所示,共计80个钢管柱计算模型.
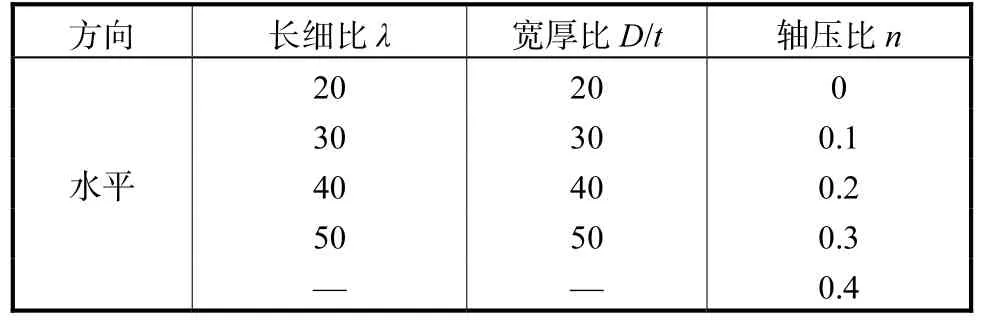
表6 钢管柱计算模型的参数Tab.6 Parameters of steel pipe column calculation models
采用ABAQUS 非线性有限元分析软件建立钢管柱的三维计算模型,钢管柱下端固定、上端自由.为了保证计算结果的可靠性,采用与缩尺模型试验对比相同的单元类型和材料本构关系.为了控制计算结果的精度,壳元边长不大于50 mm.根据钢管柱管壁的低阶屈曲模态,考虑初始缺陷的影响,其最大幅值根据现行《钢结构工程施工质量验收规范》(GB 50205—2001)[18]中对钢管构件外形尺寸允许偏差的相关规定确定.
在水平往复推覆作用下,钢管柱的加载制度与缩尺模型试验相似,采用柱顶形心位移加载控制,钢材屈服前变形角增量为1/600,屈服后变形角增量改为1/150,每级加载循环3 次.根据《建筑抗震试验方法规程》(JGJ 101—2015)[15],将最大承载力下降15%相应的变形角作为钢管柱的极限变形角.
3.2 钢管柱的屈服变形角与极限变形角
在长细比λ=20~50、径厚比D/t=20~50 以及轴压比n=0~0.4 范围内,有限元分析得到钢管柱屈服变形角θy的计算结果见表7.由表7 可知,除长细比最小(λ=20)、轴压比最大(n=0.4)时极个别钢管柱的屈服变形角接近或超过1/250 外,其他均远小于1/250 的层间位移角限值.其中,长细比影响最大,轴压比次之,径厚比影响最小.当长细比不小于40 时,屈服变形角均不大于1/150;减小轴压比有利于增大钢管柱的屈服变形角.
在长细比λ=20~50、径厚比D/t=20~50 以及轴压比n=0~0.4 范围内,有限元分析得到钢管柱极限变形角θu的计算结果见表8.由表8 可知,钢管柱极限变形角θu在1/12.4~1/54.5 范围内变化,除长细比最小(λ=20)、径厚比最大(D/t=50)和轴压比最大(n=0.4)极个别情况略大于1/50 外,均能满足不小于1/50 层间位移角限值的要求.其中,径厚比对钢管柱极限变形能力的影响最大,轴压比次之,长细比影响最小.当轴压比不超过0.2、径厚比不大于30 时,钢管柱极限变形角可以达到1/30 的性能目标;增大长细比有利于改善钢管柱的变形性能.
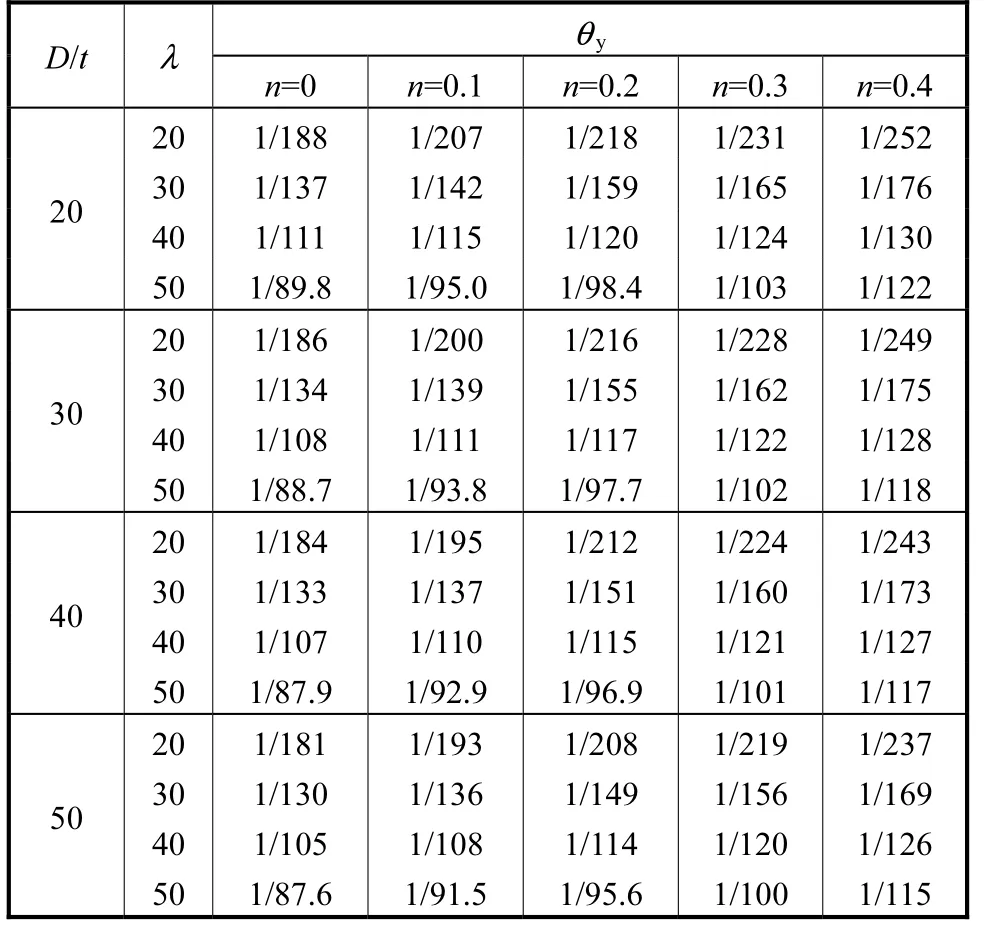
表7 钢管柱屈服变形角θy 随长细比、径厚比和轴压比的变化Tab.7 Yielding deformation angle θy of steel pipe columns vs slenderness,diameter-thickness ratio and axial compression ratio
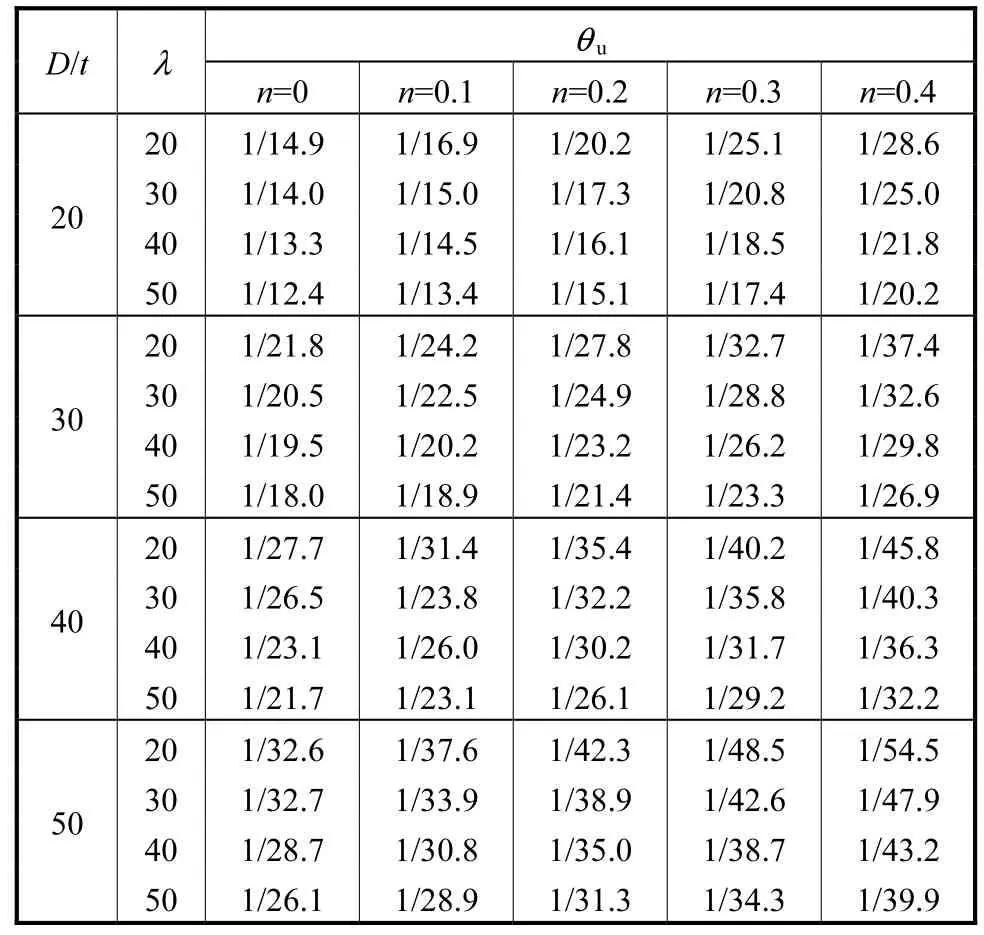
表8 钢管柱极限变形角θu 随长细比、径厚比和轴压比的变化Tab.8 Ultimate deformation angle θu of steel pipe columns vs slenderness,diameter-thickness ratio and axial compression ratio
由于钢管柱变形性能受轴压比、长细比和径厚比等参数的影响非常显著,为了便于定量估算钢管柱在水平往复荷载作用下的变形能力,通过拟合表7 与表8 有限元计算分析的结果,分别得到钢管柱屈服变形角yθ′和极限变形角uθ′与参数λ、D/t和n的关系为

按照式(2)和式(3)估算钢管柱的变形角与有限元分析结果误差不大于5.0%,可决系数r2和相关系数r非常接近1.0,标准差SD 接近于0,如表9 所示,表明拟合公式与样本的符合程度很好.

表9 钢管柱变形角拟合公式准确性验证Tab.9 Accuracy verification of the fitting formulas for deformation angle of steel pipe columns
3.3 轴压比影响
在水平往复荷载作用下,λ=30、D/t=30 时钢管柱骨架曲线随轴压比的变化见图12.由图12 可知,随着轴压比n增大,钢管柱的屈服荷载稍有降低,屈服时的变形角略有减小,最大承载力和极限变形角均显著减小.
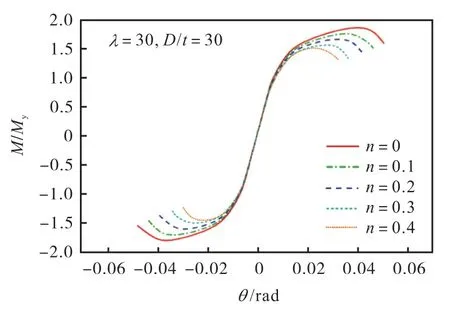
图12 钢管柱骨架曲线与轴压比的关系Fig.12 Relationship between steel pipe column skeleton curve and axial compression ratio
在水平往复荷载作用下,λ=30、D/t=30 时钢管柱变形角θy和θu随轴压比n的变化情况见图13.由图可知,钢管柱的屈服变形角θy与轴压比呈线性关系,随轴压比增大而稍有减小;极限变形角θu与轴压比略呈线性关系,随轴压比增大而显著减小;钢管柱变形角拟合公式与有限元分析结果符合情况良好.
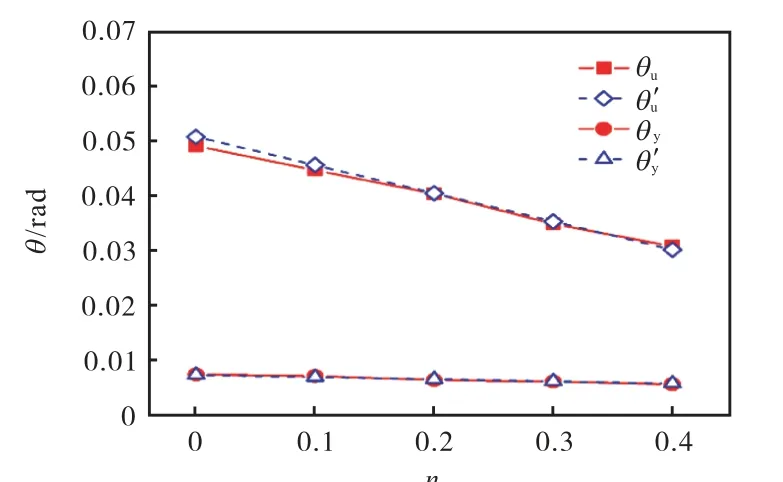
图13 钢管柱变形角θy 和θu 与轴压比n 的关系Fig.13 Relationship between steel pipe column deformation angle θy & θu and axial compression ratio n
3.4 长细比的影响
在水平往复荷载作用下,D/t=30、n=0.2 时钢管柱骨架曲线随长细比λ的变化情况见图14.由图可知,随着长细比增大,钢管柱的侧向刚度降低,屈服荷载略有减小,极限承载力明显降低,屈服变形角和极限变形角均显著增大.
在水平往复荷载作用下,D/t=30、n=0.2 时钢管柱的变形角随长细比λ的变化情况见图15.由图可知,钢管柱的屈服变形角θy和极限变形角θu与长细比λ均大致呈线性关系,随长细比增大而增大,钢管柱变形角拟合公式与有限元分析结果符合良好.

图14 钢管柱骨架曲线与长细比的关系Fig.14 Relationship between steel pipe column skeleton curve and slenderness
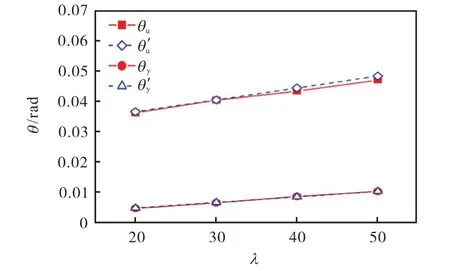
图15 钢管柱变形角θy 和θu 与长细比λ 的关系Fig.15 Relationship between steel pipe column deformation angle θy & θu and slenderness λ
3.5 径厚比的影响
在水平往复荷载作用下,λ=30、n=0.2 时钢管柱骨架曲线随径厚比D/t的变化情况见图16.由图可知,随着径厚比D/t增大,钢管柱屈服荷载和屈服变形角均变化很小,最大承载力显著降低,极限变形角急剧减小.

图16 钢管柱骨架曲线与径厚比的关系Fig.16 Relationship between steel pipe column skeleton curve and diameter-thickness ratio
在水平往复荷载作用下,λ=30、n=0.2 时钢管柱的变形角随径厚比D/t的变化情况见图17.由图可知,钢管柱的屈服变形角θy基本不受径厚比影响;极限变形角随径厚比增大而减小,两者呈非线性关系;钢管柱变形角拟合公式与有限元分析结果符合良好.

图17 钢管柱变形角θy 和θu 与径厚比的关系Fig.17 Relationship between steel pipe column deformation angle θy and θu and diameter-thickness ratio
4 结 论
(1) 当轴压比为0.2 左右时,钢管柱的滞回曲线均为较为饱满的梭形;对于同级加载,后2 次循环加载时的承载力下降很小,说明钢管柱具有良好的耗能性能.
(2) 当径厚比较小时,钢管柱塑性变形发展减缓,损伤程度下降,耗能能力增强.此外,当长细比较小时,钢管柱塑性变形发展加快,耗能能力减弱.
(3) 钢管柱进入弹塑性阶段后,底部发生环向外凸变形,随着加载过程逐渐加大;在达到极限承载力时,柱底外鼓非常显著.径厚比越大,钢管鼓曲越严重,其影响范围越靠近柱根部.
(4) 当轴压比为0.2 左右时,钢管柱试件在水平往复荷载作用下,屈服变形角和极限变形角均远大于1/250 和1/50 的规范限值;径厚比越小、长细比越大,其变形能力越强.
(5) 通过引入初始缺陷,采用随动硬化钢材的本构关系,可以较为准确地模拟钢管柱的受力性能,有限元分析结果与模型试验符合较好.
(6) 长细比对钢管柱屈服变形角的影响最大,屈服变形角与长细比λ呈线性关系,随长细比增大而显著增大;当长细比不小于40 时,屈服变形角均可以达到1/150 的性能目标.轴压比对钢管柱屈服变形角的影响次之,屈服变形角与轴压比呈线性关系,随轴压比增大而略有减小.径厚比对钢管柱屈服变形角的影响不大.
(7) 径厚比对钢管柱极限变形能力的影响最大,极限变形角与径厚比呈非线性关系,极限变形角随径厚比增大而迅速减小.轴压比对钢管柱极限变形角的影响次之,极限变形角与轴压比呈线性关系,随轴压比加大而逐渐减小;当轴压比不超过0.2、径厚比不大于30 时,钢管柱极限变形角均可以达到1/30 的性能目标.长细比对钢管柱极限变形能力的影响最小,极限变形角与长细比呈线性关系,随长细比加大而略有增大.
(8) 通过对有限元参数分析计算结果进行拟合,分别得到钢管柱屈服变形角和极限变形角的计算公式,可方便地用于钢管柱变形能力的估算.
