Appropriate search techniques to estimate Weibull function parameters in a Pinus spp. plantation

Laís Almeida Araújo · Rafael Menali Oliveira · Mário Dobner Jr ·Carolina Souza Jarochinski e Silva · Lucas Rezende Gomide

Abstract The Weibull function, a continuous probability distribution, is widely used for diameter distribution modelling, in which parameter estimation performance is af fected by stand attributes and f itting methods. The Weibull cumulative distribution function is nonlinear, and classical f itting methods may provide a not optimal solution. Invoking the use of artif icial intelligence by metaheuristics is reasonable for this optimisation task. Therefore, aimed and compared(1) the metaheuristics genetic algorithm and simulated annealing performance over the moment and percentile methods; (2) the hybrid strategy merging the metaheuristics tested and the percentile method and, (3) the metaheuristics f itness functions under basal area and density errors.A long-term experiment in a Pinus taeda stand subjected to crown thinning was used. According to our f indings,all methods have a similar performance, independent of the thinning regimes and age. The pattern of the estimated parameters tends to be acceptable, as b increases over time and c increases after thinning. Overall, our f indings suggest that methods based on metaheuristics have a higher precision than classical methods for estimating Weibull parameters. According to the classif ication test, the methods that involved simulated annealing stood out. The hybrid method involving this metaheuristic also stood out, with accurate estimates. Classical methods showed the poorest performance, and we therefore suggest the use of simulated annealing due to its faster processing time and high-quality solution.

Keywords Forest management · Diameters distribution ·Weibull function · Genetic algorithm · Simulated annealing

Introduction

Forest stand dynamics is characterised by a complex biological interaction between individual trees. Spatial distribution and resource availability change dramatically over time, resulting in altered tree growing space conditions (Li et al. 2013; Aakala et al. 2013). As a result, growth rate is af fected by inter-tree competition and also inf luenced by tree size (diameter, height and crown area), age, site, stand density, thinning, diseases, pests, natural disturbances and genetic characteristics, among others (Sánchez-Salguero et al. 2015; Ou et al. 2019). Trees are in constant competition for limited resources, such as water, minerals and light to maintain physiological functions to survive and to grow.These resource factors interact with each other, resulting in positive or negative ef fects on growth which, in turn, explain crown size and mortality rate (Weiskittel et al. 2011; Craine and Dybzinski 2013). According to Burkhart and Tomé( 2012), tree demands regarding site resources and growing space increase over time, af fecting the characteristics and variability of tree diameter distribution (Rouvinen and Kuuluvainen 2005). Consequently, considerable ef forts are made to maximise the stand prof its with optimal management regimes and silvicultural treatments. Therefore, tree diameters are still a basic variable for practical purposes such as growth and yield modelling (Bailey and Dell 1973;Loetsch et al. 1973; Poudel and Cao 2013).

Regardless of the use of individual diameters, the probability density function arranges tree size classes into frequencies (Pretzsch 2009). The subsequent distribution function simply outlines an approach for modelling the forest stand. Instead of predicting only volume or only basal area,a growth model reveals some aspects of stand structure by diameter distribution functions (Vanclay 1994). Historically,the suitability of dif ferent types of distributions has been assessed for forest type world-wide. The f irst relevant work was published in 1898 when De Liocourt proposed a simple model based on geometric progression for diameter distribution (Bailey and Dell 1973). Several probability density functions have been applied for diameter distribution modeling, for example the Exponential, Johnson’s SB, Gamma,Beta, Log-normal and Weibull functions (Liu et al. 2009).

Bailey and Dell ( 1973) were the f irst to introduce the Weibull function to f it stand diameter frequency. Over several decades, numerous publications have been written on this distribution functions in various science f ields (Rinne 2008). The success in applying the Weibull function is associated with desirable characteristics such as accuracy in f itting the observed data (Razali et al. 2009), f lexibility to describe a broad spectrum of shapes (Poudel and Cao 2013), easy of estimation of parameters (Pogoda et al.2019) and simplicity of integration methods (Burkhart and Tomé 2012). The Weibull formulation includes two or three parameters that are generally correlated to stand variables(Nokoe and Okojie 1984), and are referred as location (a),scale (b) and shape (c). Usually, the two-parameter (bandc)form of the Weibull distribution is the most simple and accurate for modelling diameter distributions in various cases(Diamantopoulou et al. 2015; Arias-Rodil et al. 2018), such asPinus taedain the USA (Bullock and Burkhart 2005),Pinus sylvestrisandPicea abiesin Finland (Maltamo et al.1995) andQuercus suberL. in Spain (Calzado-Carretero and Torres-Alvarez 2013). Variations in the Weibull distribution are also found, such as reverse Weibull; this distribution is analogous to the Weibull distribution and allows f lexibility for modelling long-tailed right-skewed data (Akgül et al.2016).

Besides the many advantages of concise Weibull properties, this function naturally tends to be non-linear in its cumulative distribution form (Huang 2000). The complexity of f itting non-linear functions is well known, leading to approximate solutions. Classic f itting methods include the maximum likelihood (Maltamo et al. 1995), moment methods (Fonton et al. 2013), percentiles method (Maltamo et al. 2018), least squares (Leduc et al. 2001), and linear and nonlinear regression (Berger and Lawrence 1974). According to Cao ( 2004), various methods have been developed to predict the Weibull parameters, either directly or indirectly, but there is no clear evidence to justify the use of any of these approaches over another. However, the estimation of function parameters is an optimisation problem solved(Křivý and Tvrdík 1995), and it seems reasonable to take the advances of computational intelligence (Diamantopoulou et al. 2015) and metaheuristics (Abbasi et al. 2006; Wen et al. 2017). Considering these issues, the genetic algorithm and simulated annealing are metaheuristics widely applied to produce useful solutions in search and optimisation problems. Metaheuristics can converge good solutions with less computational time for a wide range of problems (Cheong and Koh 2019; Courchelle et al. 2019; Franzin and Stützle 2019).

This study relies on the use of metaheuristics to determine the parameters of the Weibull distribution. The dataset comprisesPinus taedaL. stands over 30 years of production and subjected to thinning regimes in southern Brazil. We aimed to (1) compare the metaheuristics genetic algorithm and simulated annealing performance over classic methods(moments and percentiles); (2) analyse the hybrid strategy merging the metaheuristics tested and the percentile method;and, (3) verify the metaheuristic functions under basal area and density errors.

Material and methods

Study site and data description

The long-term thinning experiment inPinus taedastands was carried out for growth and yield production analysis.Stands were under crown thinning regimes aimed at producing large stems and high-quality timber. The experimental site is located in the municipality of Campo Belo do Sul, southern Brazil (Fig. 1), 27°59′33″ S latitude and 50°54′16″ W longitude, approximately 950 m.a.s.l. The climate is humid subtropical ‘Cfb’ type of Köppen’s classif ication, with cool summers, well-distributed rain events and the occurrence of frosts (Alvares et al. 2013). Annual averages of temperature and precipitation are around 16 °C and 1800 mm, respectively. Most of the soils are Nitisols and Cambisols. The original forest cover was mixed ombrophilous forest, tolerant of high precipitation.

Fig. 1 Location of the municipality of Campo Belo do Sul in Santa Catarina, southern Brazil

The experimental design was a randomised complete block design with three intensities of thinning treatments(no thinning, moderate and heavy) and two replicates. There were four thinning 5, 10, 13, and 15 years after planting(1986, 1991, 1994, and 1996). The type of thinning was selection from above, also known as “crown thinning”,in which thinning intensity is def ined by the number of competing trees removed in order to favor selected potential crop trees (pct). At 5 years, 400pcts(potential crop trees)were selected and released from competition by removing one or two competitors. Further thinnings removed one competitor per crop tree. Plot sizes were ～2000 m 2 , with an inner plot for measurements of ～1000 m 2 . Initial stand density was 2500 trees/ha (2.5 × 1.6 m). Data collection focused on diameter at breast height (dbh) of all trees between 5–16,18–22 and 30 years-of-age, resulting in 13,901dbhvalues.The database had a high diameter variation af fected by thinning treatments and ages. Therefore, to analyze the diameter behaviour based on age, these were subdivided into three classes: (1) initial phase between 5 and 12 years; (2) intermediate phase between 13 and 20 years, from which it is possible to consider clear cutting to produce assortments of medium-sized logs (a common management practice forP.taedain southern Brazil); and (3) advanced stage of a production cycle 21–30 years; this is considered only in special management strategies for obtaining large-diameter logs.Details of the dataset are given in Table 1. Diameter values ranged between 2.2 and 70.8 cm, with an average of 21.3 cm and a standard deviation of ±9.0 cm. Maximum diameter growth rates was 130.0% (37.9 cm), 200.3% (39.7 cm) and 215.6% (39.6 cm). Among the dif ferent thinning intensities, the heavy strategy inf luenced tree growth more signif icantly. Additionally, removing trees over the years changed the skew and shape of the diameter distribution, which is important for testing the hypothesis of the study.

Modeling diameter frequency

Probability density functions have been widely applied in forest management. We selected the Weibull function because of its relatively simple and accurate approach to model the diameter distribution of stands. The unimodal shape was observed for all plots. Thus, a two-parameter Weibull probability density function was used for each plot individually, which was selected due to the good modelling results obtained previously for the diameter distributions of dif ferent species (Maltamo et al. 1995; Calzado-Carretero and Torres-Alvarez 2013). According to Bailey and Dell( 1973), the probability density function (pdf) and cumulative distribution forms of the Weibull function follow Eqs.( 1) and ( 2), respectively. Eq. ( 2) is obtained by taking the integral of Eq. ( 1):

Table 1 The main characteristics of data set

where,dbhis the tree diameter at breast height;bis the scale parameter, andcthe shape parameter. The non-negativity condition of parametersbandcis respected.

The non-linearity of this cumulative function requires precise methods for parameter estimation (Huang 2000).Dif ferent approaches can be used to estimate the Weibull parameter, but the statistical approaches (moments and percentiles) has been working adequately (Lei 2008; Maltamo et al. 2018). According to Shif ley and Lentz ( 1985),the method of moments is an alternative to the maximum likelihood method (MLE) and with good accuracy. The percentile method is also well def ined and widely studied. Controversial f indings in the literature suggests the superiority of MLE than other methods (Cao 2004; Nord-Larsen and Cao 2006). In contrast, Shiver ( 1988) argued that moment estimators and percentile estimators could be trusted for their purposes. However, the solution is approximated and can be improved using stochastic algorithms. A genetic algorithm and simulated annealing was applied to compare with classic methods. Finally, the ability to predict diameter distribution depend on the method of estimating the parameters and the criteria used in the comparisons (Maltamo et al. 1995), the database and size class interval (Shiver 1988). The latter factor was controlled by adopting a 1 cm range to reduce error ef fects.

Metaheuristic

Numerous real-life optimisation problems have been def ined over the years. Recently, parameter estimation problems have been explored for environmental purposes (Tashkova et al. 2012) and nonlinear regression models (Jin et al. 2016).Generally, optimisation techniques are applied according to the complexity of the assessing the function or the problem(Assad and Deep 2018). In fact, the exact solution usually requires a high computational performance, and an approximate solution is an option.

A metaheuristics is often described as a higher-level procedure for solving wide numeric problems. Unfortunately,there is no guarantee of the optimal solution, and therefore,results not optimal are obtained in a reasonable amount of times. However, the guidelines of these frameworks indicate the ability to escape from a local optimal region (Cheong and Koh 2019). They are also robust and highly f lexible for solving a range of problems (Mafarja and Mirjalili 2017). To solve the Weibull function parameter problem,the metaheuristic genetic algorithm (GA) and simulated annealing (SA) were applied. In the latter case, the variable values are f loating-point numbers that fall between positive bounds [0, +r]. We previously set +ras the higher value(100), decreasing dynamically over the iterations. The initial values of the parameters are generated randomly. Usually, these algorithms have a set of predef ined combination parameters (Liao and Li 2020 ), and are f ine-tune by performing a sensitivity studies.

The genetic algorithm (GA) of Holland ( 1975) has been widely applied for solving search and optimisation problems (Yalçınkaya et al. 2018). It is based on the principles of evolution through natural selection and on “survival of the f ittest” using a population of individuals subjected to genetic operators, such as selection, crossover and mutation.Thus, changes are made to individuals, allowing the population to reach a better area of the search space (Cheong and Koh 2019). The functioning of the GA can be demonstrated according to Fig. 2.

In this study, a population of 50 chromosomes and 100 generations was adopted in the GA following a literature review and initial parameterisation tests. The population size af fects the search procedure, the solution quality over the iterations and the computational resources. Given the population size, all individual chromosomes were generated by randomising the feasible values of each Weibull parameter.Genetic operators (selection, crossover and mutation) provide new points in the search space and move towards new areas. We used tournament selection, which randomly chose a subset of the population for crossover. In the next step, this percentage of the most-f it chromosomes (10%) was matched by two parents for gene swapping. As a result, two of fspring derived from the crossover were inserted in the population.Previously, the mutation operation was applied considering only a 10% rate. This operator randomly changes a chromosome gene, given a new basis for increasing the population diversity. In the end, the generation gap strategy was adopted to guarantee the same population size. A f itness function was progressive searched into promissory regions guiding the GA. This adaptive process is inspired in nature and measures chromosome survivability. The GA allows a diverse population of many chromosome level under the selection rules.

Fig. 2 Flowchart of the genetic algorithm; Adapted from Cheong and Koh ( 2019)

The second metaheuristic tested was simulated annealing(SA), which is based on the analogy between the simulation of the annealing of solids and the combinatorial optimisation problem. Simulated annealing is a stochastic local search algorithm that, from an initial solution, iteratively searches the neighbourhood of the current solution (Franzin and Stützle 2019). The annealing process is formed by“heating” and “cooling”, which take certain physical systems from an initial disorganised state to a minimum energy state (Courchelle et al. 2019). The adequacy of the SA to an optimisation problem involves the def inition of its specif ic components as a method for generating the neighbouring solution, an evaluation function, a cooling schedule and a stopping criterion (Abbasi et al. 2006). The functioning of the SA is shown in Fig. 3.

We adopted initial (T0) and f inal (TF ) temperatures equal to 5.0 × 10 4 °C and 2.5 × 10 1 °C, respectively, to simulate a solid thermal equilibrium. Given the current state of the solid, the actual temperature af fects the threshold value for accepting a lower-quality solution (Mafarja and Mirjalili 2017). This cooling process under stochastic rules(metropolis criterion) adopts a single solution to explore the search space. The Metropolis criterion allows the algorithm to escape from the local optimum (Franzin and Stützle 2019) because it facilitates the acceptance of lower-quality(energy) solutions, which can result in optimal solutions as processing progresses. The cooling rate used was 1%, and the f inal temperature was used as a stop criterion for the algorithm.

Fig. 3 Flowchart of the simulated annealing algorithm; Adapted from Bettinger et al. ( 2002)

The third method is a hybrid method of the metaheuristic and the percentile methods. The strategy is to identify the optimum two percentiles (1th ≤p1≤ 50th and 50th ≤p2≤ 100th) from each stand by the metaheuristics approach and then to apply the percentile method. We assume that the percentage position changes dynamically over the years(Nord-Larsen and Cao 2006; Pogoda et al. 2019). The similarity of the diameter distribution shape has not constantly af fected by age, site and silvicultural management. The metaheuristics parameter sets the following, as described previously.

We tested two functions for f itting the Weibull parameters: (1) The sum of the absolute error between observed(fo ) and estimated (fe ) diameter frequency classes was minimized; This is a common approach that acts directly on the estimation error since the search for the lowest value resulting from the summation provides better predictive performance of the method; (2) The maximum absolute distance of the distributions (observed and estimated) was minimized by the cumulative probability form. The use of this strategy was based on the Kolmogorov-Smirnov test to assess the f it from the proximity of the distribution curves. These metaheuristics were designed to minimize the f itness function (Eq. 3)or (Eq. 4). A single run for all metaheuristics is not enough due to its stochastic search procedure; therefore, we had 50 runs. The best solution/run was used for all analyses:

where,Eis error,foiis the observed value of the frequency class i,feiis the estimated value of the frequency class i,Nis the total number of classes, Max is maximum,Poiis the value of the observed cumulative probability of class i,Peiis the value of the estimated cumulative probability of class i.

Statistical approach

Regardless of the range of methods for fitting Weibull parameters, we focused on percentile and moments. Eq. ( 5)and Eq. ( 6) support the method, and no location parameter was considered. The percentile values are inf luenced by various factors such as species, age and silviculture treatments(Bullock and Burkhart 2005; Stankova and Zlatanov 2010).We assumed the 30th and 90th percentile points, according to previous tests:

where,b,andcare scale and shape parameters, respectively,ln is the Neperian logarithm;p1andp2are percentiles 1 and 2 as 30th and 90th percentile, respectively,Dp1andDp2are the diameters for the respective percentiles 1 and 2.

In the method of moments, f itting was carried out using the EnvStats package (Millard 2018). Diameter plot information (mean and standard deviation) was applied in Eq. ( 7)and Eq. ( 8) to estimate the scale and shape parameters. An iterative method was then used to minimise the dif ference between the observed coef ficients of variation and estimated through the sample moments. This way, the shape parameter was obtained, and the scale parameter could be calculated directly from Eq. ( 7) (Diamantopoulou et al. 2015):

Distribution f itting analysis

Once the distributions were predicted, f itting quality was obtained for each plot independently. The outputs of the metaheuristics methods were f irst summarized. The minimum, mean, maximum, standard deviation and coef ficient of variation were measured for each repetition and subsequently, the mean was extracted. The overall mean was carried out on the 50 runs process for each plot.

Only the best solution was considered and compared with the statistical approach. For the goodness-of-fit test,we used Kolmogorov-Sminorv (K-S) at 5% significance.The K-S test quantifies a maximum absolute distance(D) of observed and estimated distribution (Eq. 9) and compares it with the critical value. The error index (Ei)was also used to evaluate the compatibility between the observed and estimated basal area. Reynolds et al. ( 1988)described this index as the sum of the absolute deviations from the estimated and observed distributions. Usually,the weighted difference is recommended based on tree size (e.g. volume or biomass) in this function. However,a form (Eq. 10) has been defined for evaluating it without weight. Thus, the mean, standard deviation and coefficient of variation of the error-index (Ei) for the data set were calculated. The overall D and Eivalues were converted into the ranking order of the methods for each plot. We assigned integer weights (1–10) to classify from lower (1) to higher (10) methods. Regardless of age and thinning treatment, the total scores were summed up, and the decreasing order indicates the most suitable of all 10 methods. The equations were as follows:

whereEiis the error-index,Giand̂Gidenote the total basal area observed and estimated in class i, respectively.

Histograms were applied to assess the differences in the methods for detecting non-convergence fitting. The comprehensive performances of the Taylor diagram are especially useful in evaluating complex models (Taylor 2001). In this diagram, the standard deviation (SD),correlation coefficient and root-mean-square (RMS) of the observed and estimated frequencies are plotted (3D)to indicate each point. The interpretation relies on the relationship between the explained variance and the bias(Guevara and Olmedo 2018). Thus, the diagram supports the choice of the best method (Taylor 2001).

Complementary, the space search of all feasible solutions was mapped using surface response technique only for a plot. In this technique, it is possible to analyse the sensitivity of the response variable to changes in the levels of the factors of interest to be optimised. As an example, a plot 7 years old and two thinnings was used,referring to the domain of the function to be optimised;we decided to demonstrate the approximate solution of each method. Data processing and programming were performed using the R software (R CORE TEAM 2019)with the doParallel package (Ooi 2019) to optimise experimental run time. The CPU uses Intel (R) Core ™ i7-6700 CPU @ 3.40 GHz, with an installed memory (RAM) of 16.0 GB.

Results

We detected small dif ferences in the results of the Weibull function adjustment methods. The advantage of the metaheuristic approach lies in the automated method procedure and the robust results. However, all tested methods have a similar performances and close values independent of thinning regimes and stand age (Fig. 4a, b). After visual inspection of empirical diameter distributions, a unimodal shape and rare, slightly bimodal cases were identif ied. This regular diameter distribution may inf luence the results and af fect the distribution of stem diameters within a stand.Although, the data support this behaviour, and the biological tendency of all estimated parameters values was observed in each stand. The parameterbincreased over time andcincreased after the thinning, as expected. The value limits of the scale and shape parameters for each adjustment group are shown in Table 2. Analysing the results of each plotted line individually revealed a high correlation between methods.The Spearman correlation values of these values were 0.995(b) and 0.932 (c). It should be noted, however, that although only the metaheuristic method was tested, the results of the diameter distribution should be applicable.

The Taylor diagram (Fig. 4c) conf irms the similarity of all procedures displaying the statistical patterns. A close clustering is observed with overlaps points. Therefore, the correlation between all methods given by the azimuthal position of the diagram, and these values ranges from 0.9 to 9.5.The high correlation between pairs conf irms our hypothesis of using metaheuristics as an alternative to the statistical approach. In addition, the radial distance from the origin as proportional to the standard deviation. We also noted that the distances of all frequency diameter classes for observed and estimated data were relatively equal, except for the method of moment. Figure 4d explores the relationship between variables (bandc) and their error level using contour plots. The f it of the model showed 20.6 and 32.6% for the root mean square error and determination coef ficient, respectively. In this analysis, only a single forest sample (two moderate thinning, seven-year-olds stand) within all methods was isolated to present the space of possible solutions. As expected, the statistical approach is surrounded by metaheuristic solutions, and this neighbourhood space is close to the optimum solution. However, even the most skillfull method for local search (GA) is not necessarily the better solution under the stochastic view. However, these techniques are based on their strategies for space searching and escape from the local optimum. As already pointed out, hybrid methods concentrate their local search in a small region.

Fig. 4 Predicted parameters of the Weibull function within the stand and methods: ( a) Scale parameter distribution at dif ferent ages, ( b) Shape parameter distribution at dif ferent ages, ( c) Taylor diagram, and ( d) 3D surface graph to show the search space of all feasible solutions

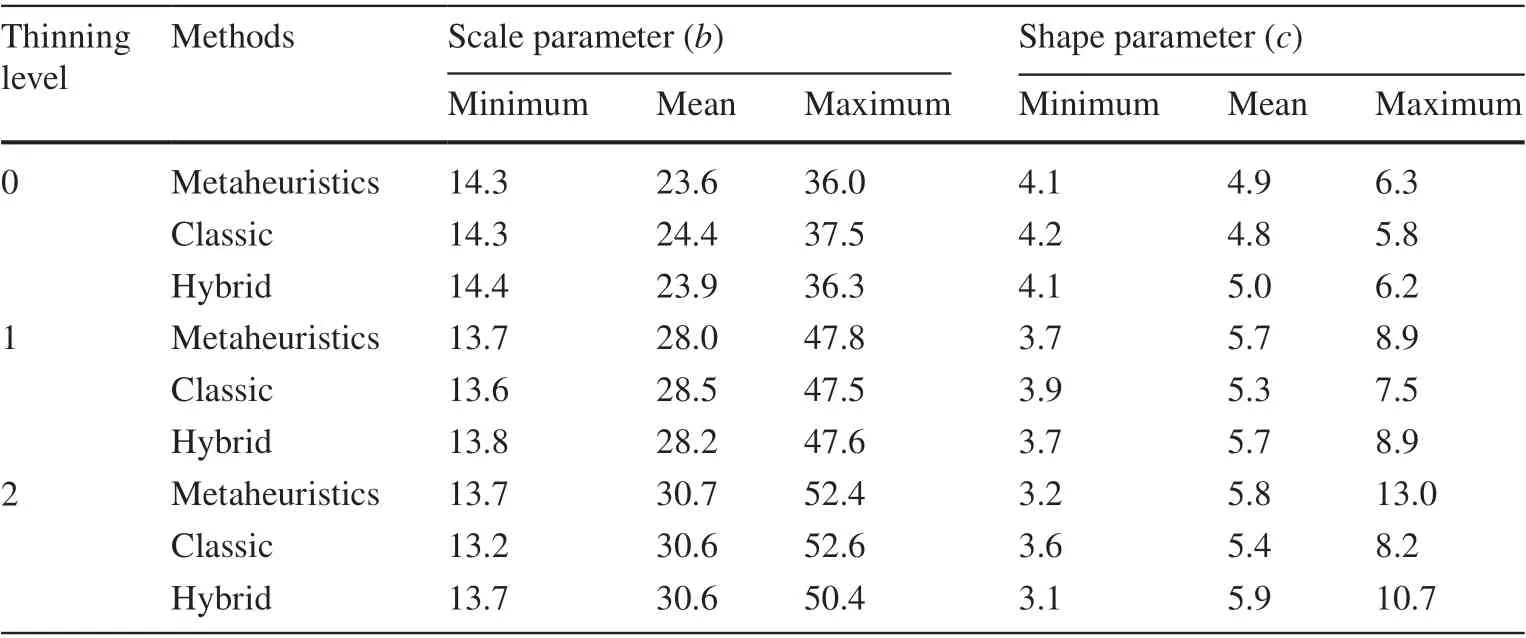
Table 2 Estimated Weibull parameters for each silvicultural regime

Metaheuristics have not failed for the convergence problem of changing the initial values until the stop criteria for all samples. Furthermore, solutions of these algorithms are sensitive the equations (Eq. 3) or (Eq. 4), inf lating the coef ficient of variation (Table 3) in this optimisation task.The lower values of this metric are associated with equation(Eq. 3) and the hybrid method. A single error point (Eq. 4)from the estimated distribution tends to be more randomness for the local space search. Regardless of the equation, the hybrid method is less af fected due to the optimum percentiles found at the f irst stage and have lower maximum values.It would seem logical to expect that the simulated annealing to be faster than the other methods, which was conf irmed.

Even though the percentiles/moments were well suited for their purpose and are distinguished from our methods,a slight dif ference was found when we analysed the set of samples individually. On the other side, the dataset did not af fect our analysis, but the considerably better f it and basal area error were associated with no thinning. The summaries of KS goodness-of-f it, error-index and ranking statistics are show in Table 4. Despite the high KS adherence of some methods, they usually resulted in a similar error for basal area estimates, most likely because we focused only on frequency class error, not basal area. Based on equations (Eq. 3)and (Eq. 4), the strategies are diverse for each metaheuristic.The f irst equation drives the search to minimise the distance of observed and estimated distribution, which af fects the shape. In this sense, all classes are reshaped together, reducing basal area error. Therefore, it probably inf luences the f it and basal area errors after predicting the Weibull parameters.The second function works similarly, minimising the maximum distance of the distributions. However, it is possible to reset the functions or further calibrate them.

Clear dif ferences among hybrid methods were found according to the rank test. The total rank summarises the overall accuracy, and the most accurate methods are, in the following order, SA 2 , SA2—percentiles and SA 1 . The opposite order was the method of moments, the method of percentiles and GA2—percentiles.

Among the classic methods, the percentiles (30th and 90th) are highlighted, since they adhered completely to the KS test in plots with moderate thinning and an overall average between treatments higher than the moments.With regard to the metaheuristics, all adjustments made with the SA2and GA2methods resulted in 100% of the function’s adherence to the data by the KS test for all thinning treatments. The same behaviour could be observed when analysing the methods using the error index (Ei).All methods displayed a similar pattern for the Eivalues,indicating a similarity in which each method captured the variation in the frequency of the diameters. However,although there was a small dif ference in errors in the basal area (0.09 m 2 /ha), the metaheuristics were superior to the classic methods. When analysing the percentage of the absolute mean error of the number of trees (N) between the methods, values between 124.9% and 142.4% were obtained for the SA1method and the moments method,respectively. The dif ference between these values (17.4%)shows an improvement in the estimates of the parameters through the metaheuristics methods compared to the classic methods.

The results of the classif ication analysis by the KS test showed that the SA 2 and SA2—percentile methods were superior to the other methods and were f irst place in the ranking. The classic moments and percentiles methods were among the last in ranking. When evaluating the classif ication from the Eivalues, a lower performance of the classic methods was also observed. According to this classif ication, the SA1and GA1methods provided more accurate estimates of basal area. In general, the moments method performed poorly in both classifications. The metaheuristic SA stood out for the two evaluation criteria,demonstrating a greater capacity of this metaheuristic to solve this type of problem.

Figure 5 shows the behaviour of the estimates of the methods with the best results per group (percentiles, SA 2 and SA2—percentiles) for a plot subjected to thinning. The greatest dif ference between the classic method and those proposed were with no or only one thinning, mainly in the middle and upper classes. This result indicates similarities between the distributions. However, metaheuristics have advantages in automated processing.

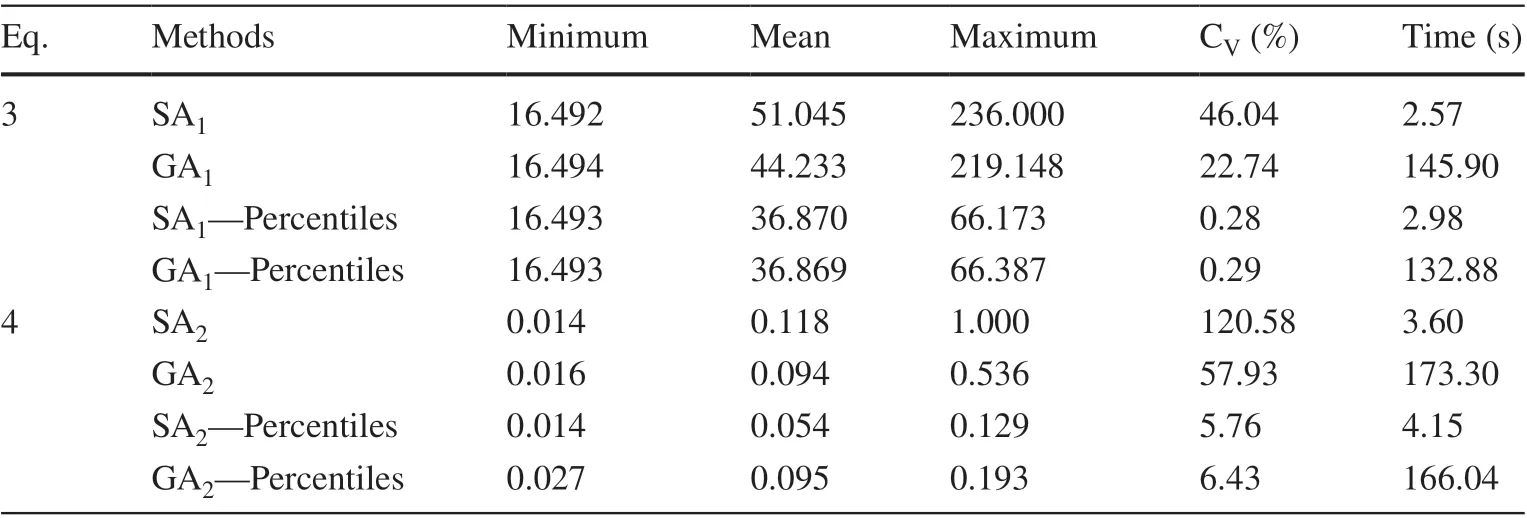
Table 3 Results of the adjustment statistics of the metaheuristic methods under the two functions performance

Table 4 Performance results of the methods for f itting Weibull parameters

Discussion

Advances in computational tools have resulted in increasingly automated approaches. Appropriately applied, the methodologies involving the use of computational intelligence can optimise the solution search process. For example, there are genetic algorithms and simulated annealing that of fer robustness in the search for the ideal solution, but demand more computational time (Cheong and Koh 2019).These metaheuristics have a high performance compared to traditional search techniques with the application to dif ferent types of problems (Yalçınkaya et al. 2018; Courchelle et al.2019).

The two-parameter Weibull function was used for the diameter distribution modelling ofPinus taedastands subjected to various thinning regimes. Dif ferent methods of obtaining the parameters and two evaluation functions were tested. The results show that the proposed new methods are an alternative to the classic methods for estimating parameters. This indicates that any of the methods can be used, with greater emphasis on the quality of the adjustment provided by the SA2, SA1and SA2—percentiles (Table 4).Previous studies have shown the applicability of metaheuristics for estimating Weibull function parameters. For example, Wen et al. ( 2017) used GA together with the maximum likelihood function, and Abbasi et al. ( 2006) applied SA to maximise the maximum likelihood function. These studies also suggest that other metaheuristics be used. Another ef fective approach was the use of the evaluation function given by Eq. ( 4), which demonstrated superiority over the others. Weber et al. ( 2006) also found a good performance with the function of minimising the Kolmogorov-Smirnov distance in a univariate probability model. In addition to the classical Kolmogorov-Smirnov statistics, the error index(E i ) was also used for basal area (Reynolds et al. 1988).In general, metaheuristics showed the lowest E i and KS values (Table 4), most likely because of the potential of metaheuristics to solve problems with non-linear relationships. The moments method presented the highest values of Eiand KS compared to the other methods. This result corroborates the work of Liu et al. ( 2009), who found that the percentile method produced lower Eiand KS statistics than the moments method and other evaluated methods.However, it contradicts the work of Lei ( 2008) for the same function, since in this case, the moments method produced the best estimate consideringPinus tabulaeformisCarr. This result also dif fers from the f indings of Fonton et al. ( 2013),who observed, for the moments method, lower values of E i and KS in dif ferent silvicultural regimes (coppice and high forest).

Fig. 5 Histograms of Pinus taeda trees and f itted Weibull function from the best methods:percentiles; SA 2 : simulated annealing (Eq. 3); and SA 2 —percentiles: simulated annealing(Eq. 4). ( a) 5 years (no thinning) ( b) 9 years (1 thinning)( c) 12 years (2 thinning) and ( d)18 years (3 thinning)

With regard to the percentile method, Adeyemi and Adesoye ( 2016) reported that the performance by this method was inf luenced by the choice of the used percentiles. Also, it is dif ficult to compare dif ferent combinations of percentiles for each data set. This problem may be solved with the hybrid method proposed in this study in which the metaheuristics evaluate dif ferent percentile values for each plot. The results found by this method showed a slight improvement in the evaluated statistics, mainly with the use of SA (Table 4).The ef ficiency of this metaheuristic is desirable since it has a good usability in the search for solution and a good adaptation to various types of problems (Assad and Deep 2018;Courchelle et al. 2019). Thus, the use of these algorithms simplif ies the process of obtaining the parameters, making it possible to test various combinations of percentiles and parameter values.

Although the evaluated methods were accurate in most cases, some of them were signif icantly dif ferent from the actual values. The responses of trees to thinning as well as age or natural disturbances may af fect the f itting rate success(Pogoda et al. 2019). These factors reduce the diameter distribution peak, making it slightly distorted and with greater variations (Nord-Larsen and Cao 2006). In addition, visual analysis showed that in some cases, the observed distributions tended to be bimodal (Fig. 5). However, the Weibull distribution is unimodal and, therefore, inadequate to model these distributions, and other forms are more indicated. Nevertheless, the tested methods are reliable and applicable.

Conclusion

Generally, modelling the diameter distribution of stands is still applicable, and the Weibull function is suitable in forest management. We present a set of promissory f itting methods for this function, with high accuracy. Metaheuristics are one approach to solve this problem and are not only applied in optimisation tasks. Consequently, it is reasonable to explore new metaheuristics or strategies for a deep space search.Finally, we suggest the use of simulated annealing to obtain faster processing times and high-quality solutions.

AcknowledgmentsLaís Almeida Araújo conceived the study and helped write the manuscript, Rafael Menali Oliveira collaborated in the def inition of the methodology, data processing and helped draft the manuscript, Mário Dobner Jr. was responsible for data collection and preparation, and helped to draft the manuscript, Carolina Souza Jarochinski e Silva helped to draft the manuscript, Lucas Rezende Gomide conducted and performed critical reviews in all stages of the work until the f inal version for submission.